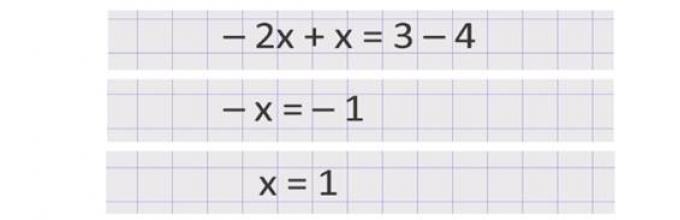Решение систем уравнений методом подстановки
Вспомним, что такое система уравнений.
Система двух уравнений с двумя переменными - это записанные друг под другом два уравнения, объединённые фигурной скобкой. Решить систему - это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.
В этом уроке познакомимся с таким способом решения систем, как способподстановки.
Давайте рассмотрим систему уравнений:
Можно решить эту систему графически. Для этого нам надо будет построить в одной системе координат графики каждого из уравнений, преобразовав их к виду:
Затем найти координаты точки пересечения графиков, которые и будут являться решением системы. Но графический способ далеко не всегда удобен, т.к. отличается малой точностью, а то и вовсе недоступностью. Попробуем рассмотреть нашу систему повнимательнее. Теперь она имеет вид:
Можно заметить, что левые части уравнений равны, а значит, должны быть равны и правые. Тогда мы получим уравнение:
Это знакомое нам уравнение с одной переменной, которое мы решать умеем. Перенесём неизвестные слагаемые в левую часть, а известные - в правую, не забыв поменять знаки +,- при переносе. Получим:
Теперь подставим найденное значение х в любое уравнение системы и найдём значение у. В нашей системе удобнее использовать второе уравнение у = 3 - х, после подстановки получим у = 2. А теперь проанализируем выполненную работу. Сначала мы в первом уравнении выразили переменную у через переменную х. Затем полученное выражение - 2х + 4 подставили во второе уравнение вместо переменной у. Потом решили полученное уравнение с одной переменной х и нашли ее значение. И в заключении использовали найденное значение х для нахождения другой переменной у. Тут возникает вопрос: а обязательно ли было выражать переменную у из обоих уравнений сразу? Конечно нет. Мы могли выразить одну переменную через другую только в одном уравнении системы и использовать его вместо соответствующей переменной во втором. Причём выразить можно любую переменную из любого уравнения. Здесь выбор зависит исключительно из удобства счёта. Подобный порядок действий математики назвали алгоритмом решения систем двух уравнений с двумя переменными методом подстановки.Вот как он выглядит.
1.Выразить одну из переменных через другую в одном из уравнений системы.
2.Подставить полученное выражение вместо соответствующей переменной в другое уравнение системы.
3.Решить полученное уравнение с одной переменной.
4.Найденное значение переменной подставить в выражение, полученное в пункте первом, и найти значение другой переменной.
5.Записать ответ в виде пары чисел, которые были найдены на третьем и четвертом шаге.
Давайте рассмотрим ещё один пример. Решить систему уравнений:
Здесь удобнее выразить переменную у из первого уравнения. Получим у = 8 - 2х. Полученное выражение надо подставить вместо у во второе уравнение. Получим:
Выпишем это уравнение отдельно и решим его. Сначала раскроем скобки. Получим уравнение 3х - 16 + 4х = 5. Соберём неизвестные слагаемые в левой части уравнения, а известные - в правой и приведём подобные слагаемые. Получим уравнение 7х = 21, отсюда х = 3.
Теперь, используя найденное значение х, можно найти:
Ответ: пара чисел (3; 2).
Таким образом, на этом уроке мы научились решать системы уравнений с двумя неизвестными аналитическим, точным способом, не прибегая к сомнительному графическому.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007.
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
Системой линейных уравнений с двумя неизвестными - это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 - некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Рассмотри один из способов решения системы линейных уравнений, а именно способ подстановки.
Алгоритм решения способом подстановки
Алгоритм решения системы линейных уравнений способом подстановки:
1. Выбрать одно уравнение (лучше выбирать то, где числа меньше) и выразить из него одну переменную через другую, например, x через y. (можно и y через x).
2. Полученное выражение подставить вместо соответствующей переменной в другое уравнение. Таким образом, у нас получится линейное уравнение с одной неизвестной.
3. Решаем полученное линейное уравнение и получаем решение.
4. Подставляем полученное решение в выражение, полученное в первом пункте, получаем вторую неизвестную из решения.
5. Выполнить проверку полученного решения.
Пример
Для того, чтобы было более понятно, решим небольшой пример.
Пример 1. Решить систему уравнений:
{x+2*y =12
{2*x-3*y=-18
Решение:
1. Из первого уравнения данной системы выражаем переменную х. Имеем x= (12 -2*y);
2. Подставляем это выражение во второе уравнение, получаем 2*x-3*y=-18; 2*(12 -2*y) - 3*y = -18; 24 - 4y - 3*y = -18;
3. Решаем полученное линейное равнение: 24 - 4y - 3*y =-18; 24-7*y =-18; -7*y = -42; y=6;
4. Подставляем полученный результат в выражение, полученное в первом пункте. x= (12 -2*y); x=12-2*6 = 0; x=0;
5. Проверяем полученное решение, для этого подставляем найденные числа в исходную систему.
{x+2*y =12;
{2*x-3*y=-18;
{0+2*6 =12;
{2*0-3*6=-18;
{12 =12;
{-18=-18;
Получили верные равенства, следовательно, мы правильно нашли решение.
Тема: Арифметическая и геометрическая прогрессии
Класс : 9
Система подготовки : материал для подготовки изучения темы по алгебре и подготовительный этап для сдачи экзамена ОГЭ
Цель : формирование понятий арифметической и геометрической прогрессии
Задачи : научить различать виды прогрессии, научить правильно, использовать формулы
Арифметической прогрессией называют последовательность чисел (членов прогрессии)
в которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии.
Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле
1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии
Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией. По этим утверждением очень просто проверить любую последовательность.
Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей
В этом легко убедиться, если расписать слагаемые справа от знака равенства
Ее часто применяют на практике для упрощения вычислений в задачах.
2) Сумма n первых членов арифметической прогрессии вычисляется по формуле
Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.
3) Если нужно найти не всю сумму, а часть последовательности начиная с k-го ее члена, то в Вам пригодится следующая формула суммы
4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k-го номера. Для этого используйте формулу
Найти сороковой член арифметической прогрессии 4;7;...
Решение:
Согласно условию имеем
Определим шаг прогрессии
По известной формуле находим сороковой член прогрессии
Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.
Решение:
Распишем заданные элементы прогрессии по формулам
Арифметическую прогрессию задано знаменателем и одним из ее членов . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых .
Решение:
Запишем формулу сотого элемента прогрессии
и найдем первый
На основе первого находим 50 член прогрессии
Находим сумму части прогрессии
и сумму первых 100
Сумма прогрессии равна 250. Найти число членов арифметической прогрессии, если:
а3-а1=8, а2+а4=14, Sn=111.
Решение:
Запишем уравнения через первый член и шаг прогрессии и определим их
Полученные значения подставляем в формулу суммы для определения количества членов в сумме
Выполняем упрощения
и решаем квадратное уравнение
Из найденных двух значений условии задачи подходит только число 8 . Таким образом, сумма первых восьми членов прогрессии составляет 111.
Решить уравнение
1+3+5+...+х=307.
Решение:
Данное уравнение является суммой арифметической прогрессии. Выпишем первый ее член и найдем разницу прогрессии
Найденные величины подставим в формулу суммы прогрессии для отыскания числа слагаемых
Как и в предыдущем задании, выполним упрощения и решим квадратное уравнение
Выбираем более логичное из двух значений. Имеем, что сумма 18 членов прогрессии с заданными величинами а1=1, d=2 равна Sn=307.
Примеры решения задач: Арифметическая прогрессия
Задача1
Студенческая бригада подрядилась выложить керамической плиткой пол в зале молодежного клуба площадью 288м2.Приобретая опыт, студенты в каждый следующий день, начиная со второго, выкладывали на 2 м2 больше чем в предыдущий, и запасов плитки им хватило ровно на 11 дней работы. Планируя, что производительность труда будет увеличиваться таким же образом, бригадир определил, что для завершения работы понадобиться еще 5 дней. Сколько коробок с плитками ему надо заказать, если 1 коробки хватает на 1,2 м2 пола, а для замены некачественных плиток понадобиться 3 коробки?
Решение
По условию задачи понятно,что речь идет об арифметической прогрессии в которой пусть
а1=х, Sn=288, n=16
Тогда используем формулу: Sn= (2а1+d(n-1))*n/0.86=200мм рт. ст.
288=(2х+2*15)*16/2
Расчитаем, сколько м2 выложат студенты за 11 дней: S11=(2*3+2*10)*11.2=143м 2
288-143=145м2осталось после 11 дней работы,т.е. на 5дней
145/1,2=121(приближенно) коробок нужно заказать на 5 дней.
121+3=124 коробки нужно заказать с учетом брака
Ответ:124 коробки
Задача2
После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда после шести движений поршня, если первоначально давление было 760 мм рт. ст.
Решение
Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха,то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде послеочередного движения поршня, нужно давление предыдущего движения поршня уиножить на 0,8.
Мы имеем геометрическую прогрессию,первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм. рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно 760*0.86=200мм.рт. ст.
Ответ:200 мм.рт.ст.
Задана арифметическая прогрессия, где пятый и десятый члены равны соответственно 38 и 23. Найти пятнадцатый член прогрессии и сумму ее десяти первых членов.
Решение:
Найти число членой арифметической прогресии 5,14,23,...,, если ее -ый член равен 239.
Решение:
Найти число членов арифметической прогресии 9,12,15,...,, если ее сумма равна 306 .
Решение:
Найдите х, при котором числа х-1, 2х-1, х2-5 составляют арифметическую прогрессию
Решение:
Найдем разность 1 и 2 членов прогрессии:
d=(2x-1)-(x-1)=x
Найдем разность 2 и 3 членов прогрессии:
d=(x2-5)-(2x-1)=x2-2x-4
Т.к. разность одинакова, то и члены прогрессии можно приравнять:
При проверке в обоих случаях получается арифметическая прогрессия
Ответ: при х=-1 и х=4
Арифметическая прогрессия задана третьим и седьмым ее членом a3=5; a7=13. Найти первый член прогрессии и сумму десяти.
Решение:
От второго уравнения вычтем первое, в результате найдем шаг прогрессии
a1+6d-(a1+2d)=4d=13-5=8, значит d=2
Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии
Вычисляем сумму первых десяти членов прогрессии
S10=(2*1+(10-1)*2)*10/2=100
Ответ: а1=1; S10=100
В арифметической прогрессии, первый член которой равен -3,4, а разность равна 3, найдите пятый и одиннадцатый члены .
Итак, мы знаем, что a1 = -3,4; d = 3. Найти: a5, a11-.
Решение. Для нахождения n-ого члена арифметической прогрессии воспользуемся формулой: an = a1+ (n – 1)d. Имеем:
a5 = a1 + (5 – 1)d = -3,4 + 4 · 3 = 8,6;
a11 = a1 + (11 – 1)d = -3,4 + 10 · 3 = 26,6.
Как видим, в данном случае, решение не сложное.
Двенадцатый член арифметической прогрессии равен 74, а разность равна -4. Найдите тридцать четвертый член данной прогрессии.
Нам сказано, что a12 = 74; d = -4, а найти надо a34-.
В данной задаче сразу применить формулу an = a1 + (n – 1)d не представляется возможным, т.к. не известен первый член a1. Такая задача может быть решена в несколько действий.
1. С помощью члена a12 и формулы n-ого члена находим a1:
a12 = a1 + (12 – 1)d, теперь упростим и подставм d: a12 = a1 + 11 · (-4). Из этого уравнения находим a1: a1 = a12 – (-44);
Двенадцатый член нам известен из условия задачи, поэтому без проблем вычисляем a1
a1 = 74 + 44 = 118. Переходим ко второму действию – вычислению a34.
2. Опять же по формуле an = a1 + (n – 1)d, так как уже известно a1, будем определять a34-,
a34 = a1 + (34 – 1)d = 118 + 33 · (-4) = 118 – 132 = -14.
Ответ: тридцать четвертый член арифметической прогрессии равен -14.
Как видно, решение второго примера более сложное. Два раза используется одна и та же формула для получения ответа. Но все так сложно. Решение можно сократить, если использовать дополнительные формулы.
Как уже отмечалось, если в задаче известно a1, то формулу для определения n-ого члена арифметической прогрессии применять очень удобно. Но, если в условии задан не первый член, то на помощь может прийти формула, которая связывает между собой нужный нам n-ый член и заданный в задаче член ak.
an = ak + (n – k)d.
Решим второй пример, но уже с использованием новой формулы.
Дано: a12 = 74; d = -4. Найти: a34-.
Используем формулу an = ak + (n – k)d. В нашем случае будет:
a34 = a12 + (34 – 12) · (-4) = 74 + 22 · (-4) = 74 – 88 = -14.
Ответ в задаче получен значительно быстрей, потому что не пришлось выполнять дополнительных действий и искать первый член прогрессии.
С помощью приведенных выше формул можно решать задачи по вычислению разности арифметической прогрессии. Так, применяя формулу an = a1 + (n – 1)d можно выразить d:
d = (an – a1) / (n – 1). Однако задачи с заданным первым членом встречаются не так часто, и решать их можно применяя нашу формулу an = ak + (n – k)d, из которой видно, что d = (an – ak) / (n – k). Давайте рассмотрим такую задачу.
Найдите разность арифметической прогрессии, если известно, что a3 = 36; a8 = 106.
Используя полученную нами формулу, решение задачи можно записать в одну строчку:
d = (a8 – a3) / (8 – 3) = (106 – 36) / 5 = 14.
Не будь в арсенале этой формулы, решение задачи заняло бы гораздо больше времени, т.к. пришлось бы решать систему двух уравнений.
Геометрические прогрессии
1. Формула -го члена (общего члена прогрессии) .
2. Формула суммы первых членов прогрессии: . При принято говорить о сходящейся геометрической прогрессии; в этом случае можно вычислить сумму всей прогрессии по формуле .
3. Формула "среднего геометрического": если , , - три последовательных члена геометрической прогрессии, то в силу определения имеем соотношения: или или 
.
Конспект урока алгебры в 9 классе
Тема урока: Определение арифметической и геометрической прогрессии.
Формула n-ого члена арифметической и геометрической
прогрессии.
Тип урока : урок изучения нового материала
Цель урока:
Формирование понятий арифметической и геометрической прогрессии, как видов числовых последовательностей; вывод формулы n-ого члена арифметической и геометрической последовательности.
Знакомство с характеристическим свойством членов арифметической и геометрической прогрессии.
Формирование умений учащихся использовать полученные знания при решении задач.
Задачи
урока:
Образовательные: ввести понятия арифметической и геометрической прогрессии; формулы n-го члена; характеристическое свойство, которым обладают члены арифметической и геометрической прогрессий.
Развивающие: повышать сознательное усвоение материала посредством противопоставления; вырабатывать умение сравнивать математические понятия, находить сходства и различия, видеть закономерности, проводить рассуждения по аналогии, развивать память и логическое мышление.
Воспитательные: создать условия для развития познавательного интереса к предмету .
План урока:
1. Организация начала урока, постановка целей и задач урока.
2. Мотивация к изучению темы («Легенда о шахматной доске»)
3. Изучение нового материала
4. Первичное закрепление
5. Подведение итогов урока
6. Домашнее задание
Ход урока
1. Организация начала урока.
Назвать тему урока, цель урока, поставленные задачи.
2. Мотивация к изучению темы.
«Легенда о шахматной доске».
Шахматы -одна из самых древних игр. Она существует уже многие века, и не удивительно, что с нею связаны предания, правдивость которых за давностью времени невозможно проверить. Одну из подобных легенд я и хочу рассказать. Чтобы понять ее, не нужно вовсе уметь играть в шахматы - достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель - его звали Сета - явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,- сказал царь.
Мудрец поклонился.
Я достаточно богат, чтобы исполнить самое смелое твое пожелание,- продолжал царь.- Назови награду, которая тебя удовлетворит, и ты получишь ее.
Сета молчал.
Не робей,- ободрил его царь.- Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!
Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
Повелитель,- сказал Сета,- прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
Простое пшеничное зерно? - изумился царь.
Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью - четыре, за четвертую - 8, за пятую- 16, за шестую - 32...
Довольно! - с раздражением прервал его царь.- Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.
Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.
Повелитель,- был ответ,- приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.
Царь нахмурился - он не привык, чтобы повеления его исполнялись так медлительно.
Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.
Повелитель,- ответили ему,- математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.
Почему медлят с этим делом?! - гневно воскликнул царь.- Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.
Прежде чем скажешь о твоем деле,- объявил Шерам.- я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.
Ради этого я и осмелился явиться перед тобой в столь ранний" час,- ответил старик.- Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико...
Как бы велико оно ни было,- надменно перебил царь,- житницы мои не оскудеют! Награда обещана и должна быть выдана...
Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.
С изумлением внимал царь словам старца.
Назови же мне это чудовищное число,-сказал он в раздумье.
Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель! (18 446 744 073 709 551 615)
Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, но что награда, о которой говорит предание, должна была выразиться именно таким числом.
Если желаете представить себе всю огромность этого числового великана, прикиньте, какой величины амбар потребовался бы для вмещения подобного количества зерен. Известно, что кубический метр пшеницы вмещает около 15 миллионов зерен. Значит, награда шахматного изобретателя должна была бы занять объем примерно в
12 000 000 000 000 куб. м, или 12 000 куб. км. При высоте амбара 4 м и ширине 10 м длина его должна была бы простираться на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца!
Конечно, индийский царь не в состоянии был выдать подобной награды.
3. Изложение нового материала.
Раздать каждому учащемуся листы, на которых изложен теоретический материал в виде таблицы, показывающей различия в определениях арифметической и геометрической прогрессий, их характеристических свойств, формулах нахождения n-ого члена, формулах для нахождения суммы n-первых членов и для геометрической прогрессии дана формула суммы бесконечно убывающей геометрической прогрессии.
Арифметическая прогрессия (а/п) | Геометрическая прогрессия (г/п) |
Опр. Арифметической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. Например: -6; -4; -2; 0; 2; 4;… 6; = -4; = -2; =0; = 2… | Опр. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число, не равное нулю. Например: 5; 15; 45; 135, … 5; =15; =45; =135; … |
d = 2 – разность а/п d = - ; d = - | q = 3 – знаменатель г/п q = ; Q = |
Формула n-ого члена а/п D = + 2 d ; D = + 3 d ; = + 4 d ; | Формула n-ого члена г/п Q = ; Q = ; |
Формула среднего члена а/п |
АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ.
Урок в 9 классе.
Учитель математики- Приходько Галина Владимировна
Цели урока:
Образовательные: совершенствовать умения по использованию формул арифметической и геометрической прогрессий для решения задач прикладного содержания, показать использование формул прогрессий для задач физики, биологии, экономики, проверка усвоения знаний путем проведения самостоятельной работы в тестовой форме.
Воспитательные: воспитывать чувство ответственности, взаимоуважения, умения работать в группах.
Развивающие: развивать интерес к предмету, потребность к получению новых знаний.
Тип урока: круглый стол.
Ход урока:
1.) Организационный момент. Учащиеся образовали группы: кафедра теории, кафедра истории, биологии, физики, экономики.
2.)Опрос. Кафедра теории.
План опроса: Определение, свойства, формула n -ого члена, формула суммы.
Арифметическая прогрессия. Геометрическая прогрессия.
1. 1. 
2. 
2. 
3. 
3. 
4. 
4. 
5. 
5. 
3.) Кафедра истории.
С понятием последовательностей связаны имена следующих математиков. Члены последовательности 1,1,2,3,5,8,13,21,34,55,89,… называют числами Фибоначчи. Это объясняется тем, что итальянский математик и купец Леонардо Пизанский (Фибоначчи) первым установил связь между этой последовательностью и известной задачей о размножении кроликов. В этой задаче исследуется численность потомства одной пары кроликов, которая ежемесячно приносит пару крольчат, а те через месяц также начинают производить потомство.
С тех пор как Фибоначчи открыл свою последовательность, были найдены явления природы, в которых эта последовательность играет немаловажную роль. Одно из них филлотаксис (листорасположение)- правило, по которому располагаются, например, семечки в соцветии подсолнуха. Семечки упорядочены в два ряда спиралей, одна из которых идёт по часовой стрелке, другая против. И количество семян в каждом случае 34 и 55, однако встречаются и гиганты с 89 и 144 семечками. Подобное свойство можно обнаружить в структуре сосновых шишек. То же наблюдается и на плодах ананаса.
Выдающийся немецкий математик К.Гаусс нашел сумму арифметической прогрессии
1, 2, 3, …, 98,99,100 в возрасте 5 лет.
С геометрической последовательностью 1, 2, 
связана старинная легенда. Индийский мудрец, придумавший шахматную игру, попросил у раджи за своё изобретение, на первый взгляд, скромное вознаграждение: за первую клетку шахматной доски 1 пшеничное зёрнышко, за вторую – 2, за третью – 4 и т. д. – за каждую следующую клетку вдвое больше, чем за предыдущую. Общее количество зерен, которое попросил изобретатель, равно 
Богатый раджа был потрясен, когда узнал, что он не в состоянии удовлетворить «скромное желание» мудреца. Значение этого выражения равно 18 446 744 073 709 551 615 т.е. 18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615.
Для того, чтобы осознать, насколько велико это число, представим, что зерно хранят в амбаре площадью 12 га. Его высота была бы больше расстояния от Земли до Солнца.
4.) Кафедра биологии.
В биологии тоже есть явления, которые можно охарактеризовать с помощью прогрессий. В частности размножение живых организмов. Зная такие характеристики организма, как периодичность размножения и численность потомства, можно с помощью прогрессий спрогнозировать количество популяции за определённый промежуток времени. Такой процесс рассматривается в следующей задаче.
ЗАДАЧА.
Бактерия, попав в организм, до конца 20 минуты делится на две, каждая из которых до конца 20 минуты снова делится на две и т.д. Сколько бактерий будет в организме через сутки?
Решение:
Количество бактерий каждые 20 минут увеличивается в 2 раза, поэтому имеем:
1,2,4,8,… геометрическая прогрессия, в которой
по формуле найдём
бактерий.
Ответ: 
бактерий.
5.) Кафедра физики.
Из истории астрономии известно, что И.Тициус, немецкий астроном 
XVIII
века, с помощью ряда чисел Фибоначчи нашёл закономерность и порядок в расстояниях между планетами солнечной системы. Однако один случай, который казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Сосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов, произошло это после смерти Тициуса в начале XIX
века.
Прогрессии выражают законы некоторых физических явлений. Например, по закону геометрической прогрессии происходит ударная ионизация. При ударной ионизации положительный ион достигая поверхности отрицательного электрода выбивает электрон. Этот электрон, обладая большой энергией выбивает электрон из внешней оболочки атома, который встречает на своём пути. Образовавшиеся уже 2 электрона выбивают ещё 2, полученные 4 ещё 4 и т. д. Образуется электронная лавина, растущая в геометрической прогрессии.
В физике есть понятие равноускоренного движения. Если тело движется равноускоренно, то расстояние, которое оно проходит за каждую следующую единицу времени, увеличивается на одну и ту же величину. Т.е. отрезки пути, которые проходит тело за 1,2,3,4,…единицы времени образуют арифметическую прогрессию.
ЗАДАЧА.
Шар, который катится в желобе, за первую секунду проходит 0,6 м. а за каждую следующую на 0,6м больше. За какое время он пройдёт 6м?
Решение: 
м, 
м, 
м.
5 не удовлетворяет условию задачи
Шар пройдёт 6м за 4сек.
Ответ:4сек.
6.)Кафедра экономики.
Первый банк был основан в Венеции в 1171 году. С тех пор банковская система развивается и усовершенствуется.
В случае размещения в банке денежного вклада вкладчик получает определённый процент за использование своих средств.
ЗАДАЧА.
Банк выплачивает 2% годовых. Какой будет сумма вклада в 800р в конце каждого года? За первый или за второй год прирост вклада больше? Каким будет вклад через 3 года?
Решение:
Пусть A
– начальный вклад, на который насчитывается p
% годовых, тогда A
·
-прирост вклада, через год имеем
где 
- стала величиной постоянной для любой суммы. Через 2 года имеем:
т.е. прирост вклада возрастает по закону геометрической прогрессии.
Если вкладчик положил в банк 800р, под 2% годовых, то прирост образует
800·0,02=16 р
За первый год сумма вклада равна 800+16 =816р
За второй год 816·(1+0.02)² = 832,32р
За каждый год начальный вклад увеличивается на 2% , поэтому через 3года он равен
800·(1,02)³= 800·1,06=848(р)
Ответ: 848р.
ЗАДАЧА.
Работники получили задание выкопать колодец. За первый выкопанный в глубину метр колодца им платят 50 р, а за каждый следующий на 20 р больше, чем за предыдущий. Сколько денег (в рублях) заплатят работникам за выкопанный колодец глубиной 12м?
Решение:
Из условия задачи имеем арифметическую прогрессию
необходимо найти 
Ответ: 1920р.
7) Решение тестовых заданий.
1 вариант.
1. Найдите разность арифметической прогрессии, если 
А) 0,9 ; Б) -0,9; В) 9; Г) -9.
2. Чему равна сумма первых четырёх членов геометрической прогрессии, первый член которой 
а знаменатель 
А) 70; Б) 85; В) 80; Г) 75.
3. Чему равна сумма шести первых членов арифметической прогрессии, если 
А)85; Б) 95; В) 105; Г) 115.
4. Среди данных последовательностей укажите арифметическую прогрессию.
А) 5;8;13;18; В) 0,1;0,2;0,3;0,4;
Б) 45;40;33;27; Г) 7;9;12;14.
5. Из последовательности чисел -9,-8,-6,4,5,6 выбрали два числа и нашли их произведение. Какое наименьшее значение может принимать это произведение?
А)-40; Б) -54; В) -72; Г) -36.
6. Укажите среди данных последовательностей геометрическую прогрессию.
А)6;18;54;162; Б)1;2;3;5; В)3;8;13;18; Г)21;19;17;15.
7. Чему равен третий член геометрической прогрессии, первый член которой 
а знаменатель 
А) 15; Б) 45; В) 135; Г) 75.
8. Найдите знаменатель геометрической прогрессии,если 
А) 
Б) 
В) 
Г) 
9. Найдите седьмой член арифметической пргрессии, первый член которой равен 8, а разность равна 0,5.
А) 11; Б) 10; В) 10,5; Г) 9,5.
10. Найдите первый член арифметической прогрессии, если второй член равен 2,1, а разность равна 0,7.
А) 1,4; Б)2,8; В) 0,3; Г) 14,7.
2 вариант.
1. Какая из последовательностей является арифметической прогрессией?
А) 1;2;4;8; Б)8;10;13;17; В)2;4;6;8; Г) -8;8;-8;8. а знаменатель
А) -2; Б) -6; В) 2; Г)6.
Кафедра биологии.
Задача. Бактерия, попав в организм, до конца 20 минуты делится на 2 , каждая из которых до конца 20 минуты снова делится на 2 и т. д. Сколько бактерий будет в организме через сутки?
Кафедра физики.
Задача. Шар, который катится в желобе, за первую секунду проходит 0,6 м, а за каждую следующую на 0,6 м больше. За какое время он пройдет 6 м.
Кафедра экономики.
Задача. Банк выплачивает 2% годовых. Какой будет сумма вклада в 800 гривен в конце каждого года? За первый или за второй год прирост вклада больше? Каким будет вклад через 3 года?
Кафедры истории и теории.
Задача. Работники получили задание выкопать колодец. За первый выкопанный в глубину метр колодца им платят 50 р, а за каждый следующий – на 20 р больше, чем за предыдущий. Сколько денег (в рублях) заплатят работникам за выкопанный колодец глубиной
12 м.
Литература:
1.Открытые уроки. Математика. 5,6,7,9,11кл. Выпуск 2. Авторы –составители: Ляшова Н.М.и другие. Волгоград: Учитель,2007-84с.
2. Предметные недели в школе. Математика. Составитель:Гончарова Л.В.
Волгоград: Учитель.2007-133с.
3. Сухарева Л.С. Дидактические игры на уроках математики.7-9кл. Харьков: Основа.2006-144с.
