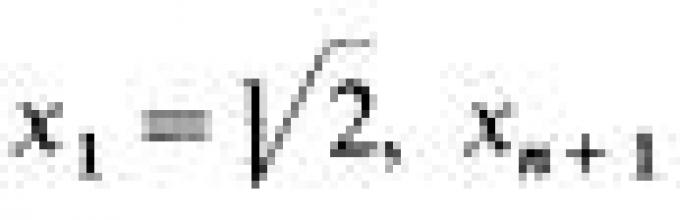Последовательность - одно из основных понятий математики. Последовательность может быть составлена из чисел, точек, функций, векторов и т.д. Последовательность считается заданной, если указан закон, по которому каждому натуральному числу n ставится в соответствие элемент x n некоторого множества. Последовательность записывается в виде x 1 , x 2 , …, x n , или кратко (x n). Элементы x 1 , x 2 , …, x n называются членами последовательности, x 1 - первым, x 2 - вторым, x n - общим (n-м) членом последовательности.
Наиболее часто рассматривают числовые последовательности, т. е. последовательности, члены которых - числа. Аналитический способ - самый простой способ задания числовой последовательности. Это делают с помощью формулы, выражающей n-й член последовательности х 1 через его номер n. Например, если
Другой способ - рекуррентный (от латинского слова recurrens - «возвращающийся»), когда задают несколько первых членов последовательности и правило, позволяющее вычислять каждый следующий член через предыдущие. Например:
Примеры числовых последовательностей - арифметическая прогрессия и геометрическая прогрессия .
Интересно проследить поведение членов последовательности при неограниченном возрастании номера n (то, что n неограниченно возрастает, записывается в виде n → ∞ и читается: «n стремится к бесконечности»).
Рассмотрим последовательность с общим членом x n = 1/n: x 1 = 1, x 2 = 1/2; x 3 = 1/3, …, x 100 = 1/100, …. Все члены этой последовательности отличны от нуля, но чем больше n, тем меньше x n отличается от нуля. Члены этой последовательности при неограниченном возрастании n стремятся к нулю. Говорят, что число нуль есть предел этой последовательности.
Другой пример: x n = (−1) n /n - определяет последовательность
Члены этой последовательности также стремятся к нулю, но они то больше нуля, то меньше нуля - своего предела.
Рассмотрим еще пример: x n = (n − 1)/(n + 1). Если представить x n в виде
то станет понятно, что эта последовательность стремится к единице.
Дадим определение предела последовательности. Число a называется пределом последовательности (x n), если для любого положительного числа ε можно указать такой номер N, что при всех n > N выполняется неравенство |x n − a| < ε.
Если a есть предел последовательности (x n), то пишут x n → a, или a = lim n→∞ x n (lim - три первые буквы латинского слова limes - «предел»).
Это определение станет понятнее, если ему придать геометрический смысл. Заключим число a в интервал (a − ε, a + ε) (см. рис.). Число а есть предел последовательности (x n), если независимо от малости интервала (a − ε, a + ε) все члены последовательности с номерами, бо́льшими некоторого N, будут лежать в этом интервале. Иными словами, вне любого интервала (a − ε, a + ε) может находиться лишь конечное число членов последовательности.
Для рассмотренной последовательности x n = (−1) n /n в ε-окрестность точки нуль при ε = 1/10 попадают все члены последовательности, кроме первых десяти, а при ε = 1/100 - все члены последовательности, кроме первых ста.
Последовательность, имеющая предел, называется сходящейся, а не имеющая предела - расходящейся. Вот пример расходящейся последовательности: x n = (−1) n . Ее члены попеременно равны +1 и −1 и не стремятся ни к какому пределу.
Если последовательность сходится, то она ограничена, т. е. существуют такие числа c и d, что все члены последовательности удовлетворяют условию c ≤ x n ≤ d. Отсюда следует, что все неограниченные последовательности расходящиеся. Таковы последовательности:
Стремящаяся к нулю последовательность называется бесконечно малой. Понятие бесконечно малой может быть положено в основу общего определения предела последовательности, так как предел последовательности (x n) равен a тогда, и только тогда, когда x n представимо в виде суммы x n = a + α n , где α n бесконечно малая.
Рассмотренные последовательности (1/n), ((−1) n /n) являются бесконечно малыми. Последовательность (n − 1)/(n + 1), как следует из (2), отличается от 1 на бесконечно малую 2/(n + 1), и потому предел этой последовательности равен 1.
Большое значение в математическом анализе имеет также понятие бесконечно большой последовательности. Последовательность (x n) называется бесконечно большой, если последовательность (1/x n) бесконечно малая. Бесконечно большую последовательность (x n) записывают в виде x n → ∞, или lim n→∞ x n = ∞, и говорят, что она «стремится к бесконечности». Вот примеры бесконечно больших последовательностей:
(n 2), (2 n), (√(n + 1)), (n - n 2).
Подчеркнем, что бесконечно большая последовательность не имеет предела.
Рассмотрим последовательности (x n) и (y n). Можно определить последовательности с общими членами x n + y n , x n − y n , x n y n и (если y n ≠ 0) x n /y n . Справедлива следующая теорема, которую часто называют теоремой об арифметических действиях с пределами: если последовательности (x n) и (y n) сходящиеся, то сходятся также последовательности (x n + y n), (x n − y n), (x n y n), (x n /y n) и имеют место равенства:
В последнем случае необходимо потребовать, кроме того, чтобы все члены последовательности (y n) были отличны от нуля, еще и чтобы выполнялось условие lim n→∞ y n ≠ 0.
Применяя эту теорему, можно находить многие пределы. Найдем, например, предел последовательности с общим членом
Представив x n в виде
установим, что предел числителя и знаменателя существует:
поэтому получим:
lim n→∞ x n = 2/1 =2.
Важный класс последовательностей - монотонные последовательности. Так называют последовательности возрастающие (x n+1 > x n при любом n), убывающие (x n+1 < x n), неубывающие (x n+1 ≥ x n) и невозрастающие (x n+1 ≤ x n). Последовательность (n − 1)/(n + 1) возрастающая, последовательность (1/n) убывающая. Можно доказать, что рекуррентно заданная последовательность (1) монотонно возрастает.
Представим себе, что последовательность (x n) не убывает, т. е. выполняются неравенства
x 1 ≤ x 2 ≤ x 3 ≤ … ≤ x n ≤ x n+1 ≤ …,
и пусть, кроме того, эта последовательность ограничена сверху, т. е. все x n не превосходят некоторого числа d. Каждый член такой последовательности больше предыдущего или равен ему, но все они не превосходят d. Вполне очевидно, что эта последовательность стремится к некоторому числу, которое либо меньше d, либо равно d. В курсе математического анализа доказывается теорема, что неубывающая и ограниченная сверху последовательность имеет предел (аналогичное утверждение справедливо для невозрастающей и ограниченной снизу последовательности). Эта замечательная теорема дает достаточные условия существования предела. Из нее, например, следует, что последовательность площадей правильных n-угольников, вписанных в окружность единичного радиуса, имеет предел, так как является монотонно возрастающей и ограниченной сверху. Предел этой последовательности обозначается π.
С помощью предела монотонной ограниченной последовательности определяется играющее большую роль в математическом анализе число е - основание натуральных логарифмов:
е = lim n→∞ (1 + 1/n) n .
Последовательность (1), как уже отмечалось, монотонная и, кроме того, ограничена сверху. Она имеет предел. Мы легко найдем этот предел. Если он равен a, то число а должно удовлетворять равенству a = √(2 + a). Решая это уравнение, получаем a = 2.
Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.
Постоянное число а называется пределом последовательности {x n}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x n , у которых n>N, удовлетворяют неравенству
Записывают это следующим образом: или x n → a.
Неравенство (6.1) равносильно двойному неравенству
a - ε < x n < a + ε которое означает, что точки x n , начиная с некоторого номера n>N, лежат внутри интервала (a-ε , a+ε), т.е. попадают в какую угодно малую ε-окрестность точки а .
Последовательность, имеющая предел, называется сходящейся , в противном случае - расходящейся .
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x n = f(n) целочисленного аргумента n .
Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a . Точка a может принадлежать множеству D(f), а может и не принадлежать ему.
Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {x n } значений аргумента, стремящейся к а , соответствующие им последовательности {f(x n)} имеют один и тот же предел А.
Это определение называют определением предела функции по Гейне, или “на языке последовательностей ”.
Определение 2
. Постоянное число А называется предел
функции
f(x) при
x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ
>0 (зависящее от ε), что для всех x
, лежащих в ε-окрестности числа а
, т.е. для x
, удовлетворяющих неравенству
0 < x-a < ε , значения функции f(x) будут лежать в
ε-окрестности числа А, т.е. |f(x)-A| < ε
Это определение называют определением предел функции по Коши, или “на языке ε - δ "
Определения 1 и 2 равносильны. Если функция f(x) при x → a имеет предел , равный А, это записывается в виде
В том случае, если последовательность {f(x n)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а , то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:
Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной.
Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной .
Чтобы найти предел на практике пользуются следующими теоремами.
Теорема 1 . Если существует каждый предел
(6.4)
(6.5)
(6.6)
Замечание . Выражения вида 0/0, ∞/∞, ∞-∞ 0*∞ являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.
Теорема 2.
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, 
Теорема 3.
(6.11)
где e » 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.
Используются на практике и следствия формулы (6.11):
(6.12)
(6.13)
(6.14)
в частности предел,
Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x
. Функция f(x) называется непрерывной
в точке
x 0 , если предел
(6.15)
Условие (6.15) можно переписать в виде:
то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.
Если равенство (6.15) нарушено, то говорят, что при x = x o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R , кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x o)= f(0) не определено, поэтому в точке x o = 0 функция имеет разрыв.
Функция f(x) называется непрерывной справа в точке x o , если предел
и непрерывной слева в точке x o, если предел
Непрерывность функции в точке x o равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке x o , например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
1. Если предел существует и не равен f(x o), то говорят, что функция f(x) в точке x o имеет разрыв первого рода, или скачок .
2. Если предел равен +∞ или -∞ или не существует, то говорят, что в точке x o функция имеет разрыв второго рода .
Например, функция y = ctg x при x → +0 имеет предел, равный +∞ , значит, в точке x=0 она имеет разрыв второго рода. Функция y = E(x) (целая часть от x ) в точках с целыми абсциссами имеет разрывы первого рода, или скачки.
Функция, непрерывная в каждой точке промежутка , называется непрерывной в . Непрерывная функция изображается сплошной кривой.
Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.
Рассмотрим пример Я. И. Перельмана
, дающий интерпретацию числа e
в задаче о сложных процентах. Число e
есть предел 
. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода - в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 ×
(1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:
100×(1 +1/10) 10 ≈ 259 (ден. ед.),
100×(1+1/100) 100 ≈ 270 (ден. ед.),
100×(1+1/1000) 1000 ≈271 (ден. ед.).
При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел
Пример 3.1 . Пользуясь определением предела числовой последовательности, доказать, что последовательность x n =(n-1)/n имеет предел, равный 1.
Решение. Нам надо доказать, что, какое бы ε > 0 мы ни взяли, для него найдется натуральное число N, такое, что для всех n > N имеет место неравенство |x n -1| < ε
Возьмем любое ε > 0. Так как x n -1 =(n+1)/n - 1= 1/n, то для отыскания N достаточно решить неравенство 1/n<ε. Отсюда n>1/ε и, следовательно, за N можно принять целую часть от 1/ε N = E(1/ε). Мы тем самым доказали, что предел .
Пример 3.2. Найти предел последовательности, заданной общим членом
.
Решение. Применим теорему предел суммы и найдем предел каждого слагаемого. При n → ∞ числитель и знаменатель каждого слагаемого стремится к бесконечности, и мы не можем непосредственно применить теорему предел частного. Поэтому сначала преобразуем x n , разделив числитель и знаменатель первого слагаемого на n 2 , а второго на n . Затем, применяя теорему предел частного и предел суммы, найдем:
Пример 3.3
. 
. Найти .
Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.
Пример 3.4
. Найти (
).
Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:
Пример 3.5 . Дана функция f(x)=2 1/x . Доказать, что предел не существует.
Решение.
Воспользуемся определением 1 предела функции через последовательность. Возьмем последовательность { x n }, сходящуюся к 0, т.е. Покажем, что величина f(x n)= для разных последовательностей ведет себя по-разному. Пусть x n = 1/n. Очевидно, что , тогда предел 
Выберем теперь в качестве x n
последовательность с общим членом x n = -1/n, также стремящуюся к нулю. 
Поэтому предел не существует.
Пример 3.6 . Доказать, что предел не существует.
Решение.
Пусть x 1 , x 2 ,..., x n ,... - последовательность, для которой
. Как ведет себя последовательность {f(x n)} = {sin x n } при различных x n → ∞
Если x n = p
n, то sin x n = sin (p
n) = 0 при всех n
и предел Если же
x n =2
p
n+
p
/2, то sin x n = sin(2
p
n+
p
/2) = sin
p
/2 = 1 для всех n
и следовательно предел . Таким образом, не существует.
Введение………………………………………………………………………………3
1.Теоретическая часть……………………………………………………………….4
Основные понятия и термины…………………………………………………....4
1.1 Виды последовательностей…………………………………………………...6
1.1.1.Ограниченные и неограниченные числовые последовательности…..6
1.1.2.Монотонность последовательностей…………………………………6
1.1.3.Бесконечно большие и бесконечно малые последовательности…….7
1.1.4.Свойства бесконечно малых последовательностей…………………8
1.1.5.Сходящиеся и расходящиеся последовательности и их свойства..…9
1.2Предел последовательности………………………………………………….11
1.2.1.Теоремы о пределах последовательностей……………………………15
1.3.Арифметическая прогрессия…………………………………………………17
1.3.1. Свойства арифметической прогрессии…………………………………..17
1.4Геометрическая прогрессия…………………………………………………..19
1.4.1. Свойства геометрической прогрессии…………………………………….19
1.5. Числа Фибоначчи……………………………………………………………..21
1.5.1 Связь чисел Фибоначчи с другими областями знаний…………………….22
1.5.2. Использование ряда чисел Фибоначчи для описания живой и неживой природы…………………………………………………………………………….23
2. Собственные исследования…………………………………………………….28
Заключение……………………………………………………………………….30
Список использованной литературы…………………………………………....31
Введение.
Числовые последовательности это очень интересная и познавательная тема. Эта тема встречается в заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, вступительных экзаменов в Высшие Учебные Заведения и на ЕГЭ. Мне интересно узнать связь математических последовательностей с другими областями знаний.
Цель исследовательской работы: Расширить знания о числовой последовательности.
1. Рассмотреть последовательность;
2. Рассмотреть ее свойства;
3. Рассмотреть аналитическое задание последовательности;
4. Продемонстрировать ее роль в развитии других областей знаний.
5. Продемонстрировать использование ряда чисел Фибоначчи для описания живой и неживой природы.
1. Теоретическая часть.
Основные понятия и термины.
Определение. Числовая последовательность– функция вида y = f(x), x О N, где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,… называют соответственно первым, вторым, третьим, … членами последовательности.
Число a называется пределом последовательности x = {x n }, если для произвольного заранее заданного сколь угодно малого положительного числа ε найдется такое натуральное число N, что при всех n>N выполняется неравенство |x n - a| < ε.
Если число a есть предел последовательности x = {x n }, то говорят, что x n стремится к a, и пишут
.Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < ….
Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y1 > y2 > y3 > … > yn > yn+1 > … .
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство yn = yn+T . Число T называется длиной периода.
Арифметическая прогрессия- это последовательность {an}, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями
a1 = a, an = an–1 + d (n = 2, 3, 4, …)
Геометрическая прогрессия- это последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q.
Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями
b1 = b, bn = bn–1 q (n = 2, 3, 4…).
1.1 Виды последовательностей.
1.1.1 Ограниченные и неограниченные последовательности.
Последовательность {bn} называют ограниченной сверху, если существует такое число М, что для любого номера n выполняется неравенство bn≤ M;
Последовательность {bn} называют ограниченной снизу, если существует такое число М, что для любого номера n выполняется неравенство bn≥ М;
Например:
1.1.2 Монотонность последовательностей.
Последовательность {bn} называют невозрастающие (неубывающей), если для любого номера n справедливо неравенство bn≥ bn+1 (bn ≤bn+1);
Последовательность {bn} называют убывающей (возрастающей), если для любого номера n справедливо неравенство bn> bn+1 (bn Убывающие и возрастающие последовательности называют строго монотонными, невозрастающие- монотонными в широком смысле. Последовательности, ограниченные одновременно сверху и снизу, называются ограниченными. Последовательность всех этих типов носят общее название- монотонные. 1.1.3 Бесконечно большие и малые последовательности. Бесконечно малая последовательность- это числовая функция или последовательность, которая стремится к нулю. Последовательность an называется бесконечно малой, если Функция называется бесконечно малой в окрестности точки x0, если ℓimx→x0 f(x)=0. Функция называется бесконечно малой на бесконечности, если ℓimx→.+∞ f(x)=0 либо ℓimx→-∞ f(x)=0 Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если ℓimx→.+∞ f(x)=а, то f(x) − a = α(x), ℓimx→.+∞ f((x)-a)=0. Бесконечно большая последовательность- числовая функция или последовательность, которая стремится к бесконечности. Последовательность an называется бесконечно большой, если ℓimn→0 an=∞. Функция называется бесконечно большой в окрестности точки x0, если ℓimx→x0 f(x)= ∞. Функция называется бесконечно большой на бесконечности, если ℓimx→.+∞ f(x)= ∞ либо ℓimx→-∞ f(x)= ∞ . 1.1.4 Свойства бесконечно малых последовательностей. Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью. Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Любая бесконечно малая последовательность ограничена. Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю. Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы - нули. Если {xn} - бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность {1/xn} , которая является бесконечно малой. Если же всё же {xn} содержит нулевые элементы, то последовательность {1/xn} всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно малой. Если {an} - бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность {1/an}, которая является бесконечно большой. Если же всё же {an}содержит нулевые элементы, то последовательность {1/an} всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно большой. 1.1.5 Сходящиеся и расходящиеся последовательности и их свойства. Сходящаяся последовательность- это последовательность элементов множества Х, имеющая предел в этом множестве. Расходящаяся последовательность- это последовательность, не являющаяся сходящейся. Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю. Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности. Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится. Если последовательность {xn} сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность {1/xn}, которая является ограниченной. Сумма сходящихся последовательностей также является сходящейся последовательностью. Разность сходящихся последовательностей также является сходящейся последовательностью. Произведение сходящихся последовательностей также является сходящейся последовательностью. Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность. Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела. Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней. Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй. Пусть
X
{\displaystyle X}
- это либо множество вещественных чисел
R
{\displaystyle \mathbb {R} }
, либо множество комплексных чисел
C
{\displaystyle \mathbb {C} }
. Тогда последовательность
{
x
n
}
n
=
1
∞
{\displaystyle \{x_{n}\}_{n=1}^{\infty }}
элементов множества
X
{\displaystyle X}
называется числовой последовательностью
. Подпоследовательность
последовательности
(x
n)
{\displaystyle (x_{n})}
- это последовательность
(x
n
k)
{\displaystyle (x_{n_{k}})}
, где
(n
k)
{\displaystyle (n_{k})}
- возрастающая последовательность элементов множества натуральных чисел. Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов. Предельная точка последовательности
- это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом . Предел последовательности
- это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности, для числовых последовательностей предел - это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого. Фундаментальная последовательность
(сходящаяся в себе последовательность
, последовательность Коши
) - это последовательность элементов метрического пространства , в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного. Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.
3. Предел числовой последовательности
3.1. Понятие числовой последовательности и функции натурального аргумента
Определение 3.1.
Числовой последовательностью (в дальнейшем просто последовательностью) называется упорядоченное счетное множество чисел {x1, x2, x3,
... }. Обратите внимание на два момента. 1. В последовательности бесконечно много чисел. Если чисел конечное число – это не последовательность! 2. Все числа упорядочены, то есть расположены в определенном порядке. В дальнейшем для последовательности часто будем использовать сокращенное обозначение {xn
}. Над последовательностями можно производить определенные операции. Рассмотрим некоторые из них. 1. Умножение последовательности на число.
Последовательность c
×{xn
} – это последовательность с элементами {c
×
xn
}, то есть c
×{x1, x2, x3,
... }={c
×
x1, c
×
x2, c
×
x3
, ... }. 2. Сложение и вычитание последовательностей.
{xn
}±{yn
}={xn
±
yn
}, или, более подробно, {x1, x2, x3, ...
}±{y1, y2, y3, ...
}={x1
±
y1, x2
±
y2, x3
±
y3,
... }. 3. Умножение последовательностей.
{xn
}×{yn
}={xn
×
yn
}. 4. Деление последовательностей.
{xn
}/{yn
}={xn/yn
}. Естественно, предполагается, что в этом случае все yn
¹ 0. Определение 3.2.
Последовательность {xn
} называется ограниченной сверху, если https://pandia.ru/text/78/243/images/image004_49.gif" width="71 height=20" height="20">.gif" width="53" height="25 src=">.Последовательность {xn} называется ограниченной, если она одновременно ограничена и сверху и снизу. 3.2. Предел последовательности. Бесконечно большая последовательность
Определение 3.3.
Число a
называется пределом последовательности {xn
} при n
стремящимся к бесконечности, если https://pandia.ru/text/78/243/images/image007_38.gif" width="77" height="33 src=">.gif" width="93" height="33">, если . Говорят, что , если . Определение 3.4.
Последовательность {xn
} называется бесконечно большой, если (то есть, если 3.3.
Бесконечно малая последовательность.
Определение 3.5.
Последовательность {xn} называется бесконечно малой, если , то есть если . Бесконечно малые последовательности имеют следующие свойства. 1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность. 2. Бесконечно малая последовательность ограничена. 3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность. 4. Если {xn
} – бесконечно большая последовательность, то, начиная с некоторого N
, определена последовательность {1/xn
}, и она есть бесконечно малая последовательность. Наоборот, если {xn
} – бесконечно малая последовательность и все xn
отличны от нуля, то {1/xn
} есть бесконечно большая последовательность. 3.4.
Сходящиеся последовательности.
Определение 3.6.
Если существует конечный предел https://pandia.ru/text/78/243/images/image017_29.gif" width="149" height="33">. 5. Если 3.5.
Предельный переход в неравенствах.
Теорема 3.1.
Если, начиная с некоторого N
, все xn
³ b
, то . Следствие.
Если, начиная с некоторого N
, все xn
³ yn
, то Замечание
. Заметьте, что если, начиная с некоторого N
, все xn
> b
, то , то есть при предельном переходе строгое неравенство может перейти в нестрогое. Теорема 3.2.
(«Теорема о двух милиционерах») Если, начиная с некоторого N
, выполнены следующие свойства 1..gif" width="163" height="33 src=">, то существует . 3.6. Предел монотонной последовательности.
Определение 3.7.
Последовательность {xn
} называется монотонно возрастающей, если для любого n
xn+1
³ xn
. Последовательность {xn
} называется строго монотонно возрастающей, если для любого n
xn+1
> xn
. xn
. Определение 3.8.
Последовательность {xn
} называется монотонно убывающей, если для любого n
xn+1
£ xn
. Последовательность {xn
} называется строго монотонно убывающей, если для любого n
xn+1
< xn
. Оба этих случая объединяют символом xn
¯. Теорема о существовании предела монотонной последовательности.
1. Если последовательность {xn
} монотонно возрастает (убывает) и ограничена сверху (снизу), то у нее существует конечный предел, равный sup{xn
} (inf{xn
}). 2 Если последовательность {xn
} монотонно возрастает (убывает), но сверху (снизу) не ограничена, то у нее существует предел, равный +¥ (-¥). На основании этой теоремы доказывается, что существует так называемый замечательный предел https://pandia.ru/text/78/243/images/image028_15.gif" width="176" height="28 src=">. Она называется подпоследовательностью последовательности {xn
}. Теорема 3.3.
Если последовательность {xn
} сходится и ее предел равен a
, то любая ее подпоследовательность также сходится и имеет тот же самый предел. Если {xn
} – бесконечно большая последовательность, то любая ее подпоследовательность есть также бесконечно большая. Лемма Больцано - Вейерштрасса.
1. Из любой ограниченной последовательности можно извлечь такую подпоследовательность, которая сходится к конечному пределу. 2. Из любой неограниченной последовательности можно извлечь бесконечно большую подпоследовательность. На основании этой леммы доказывается один из основных результатов теории пределов – Признак сходимости Больцано-Коши.
Для того, чтобы у последовательности {xn
} существовал конечный предел, необходимо и достаточно, чтобы Последовательность, удовлетворяющая этому свойству, называется фундаментальной последовательностью, или последовательностью, сходящейся в себе.Примеры
Операции над последовательностями
Подпоследовательности
Примеры
Свойства
Предел последовательности
Фундаментальные последовательности
).
, то 
.
.
