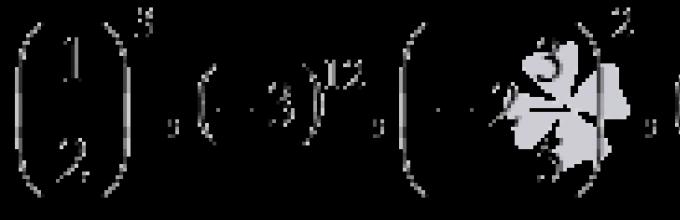В этой статье мы разберемся, что такое степень числа . Здесь мы дадим определения степени числа, при этом подробно рассмотрим все возможные показатели степени, начиная с натурального показателя, заканчивая иррациональным. В материале Вы найдете массу примеров степеней, покрывающих все возникающие тонкости.

Навигация по странице.

Степень с натуральным показателем, квадрат числа, куб числа

Для начала дадим . Забегая вперед, скажем, что определение степени числа a с натуральным показателем n дается для a , которое будем называть основанием степени , и n , которое будем называть показателем степени . Также отметим, что степень с натуральным показателем определяется через произведение, так что для понимания нижеизложенного материала нужно иметь представление об умножении чисел.

Определение.

Степень числа a с натуральным показателем n - это выражение вида a n , значение которого равно произведению n множителей, каждый из которых равен a , то есть, .
В частности, степенью числа a с показателем 1 называется само число a , то есть, a 1 =a .

Сразу стоит сказать о правилах чтения степеней. Универсальный способ чтения записи a n таков: «a в степени n ». В некоторых случаях также допустимы такие варианты: «a в n -ой степени» и «n -ая степень числа a ». Для примера возьмем степень 8 12 , это «восемь в степени двенадцать», или «восемь в двенадцатой степени», или «двенадцатая степень восьми».

Вторая степень числа, а также третья степень числа имеют свои названия. Вторую степень числа называют квадратом числа , например, 7 2 читается как «семь в квадрате» или «квадрат числа семь». Третья степень числа называется кубом числа , к примеру, 5 3 можно прочитать как «пять в кубе» или сказать «куб числа 5 ».

Пришло время привести примеры степеней с натуральными показателями . Начнем со степени 5 7 , здесь 5 – основание степени, а 7 – показатель степени. Приведем еще пример: 4,32 является основанием, а натуральное число 9 – показателем степени (4,32) 9 .

Обратите внимание, что в последнем примере основание степени 4,32 записано в скобках: чтобы избежать разночтений мы будем брать в скобки все основания степени, которые отличны от натуральных чисел. В качестве примера приведем следующие степени с натуральными показателями , их основания не являются натуральными числами, поэтому они записаны в скобках. Ну и для полной ясности в этом моменте покажем разницу, заключенную в записях вида (−2) 3 и −2 3 . Выражение (−2) 3 – это степень −2 с натуральным показателем 3, а выражение −2 3 (его можно записать как −(2 3) ) соответствует числу, значению степени 2 3 .

Заметим, что встречается обозначение степени числа a с показателем n вида a^n . При этом, если n – многозначное натуральное число, то показатель степени берется в скобки. Например, 4^9 – это другая запись степени 4 9 . А вот еще примеры записи степеней при помощи символа «^ »: 14^(21) , (−2,1)^(155) . В дальнейшем мы преимущественно будем пользоваться обозначением степени вида a n .

Одной из задач, обратной возведению в степень с натуральным показателем, является задача нахождения основания степени по известному значению степени и известному показателю. Эта задача приводит к .

Известно, что множество рациональных чисел состоит из целых и дробных чисел, причем каждое дробное число может быть представлено в виде положительной или отрицательной обыкновенной дроби. Степень с целым показателем мы определили в предыдущем пункте, поэтому, чтобы закончить определение степени с рациональным показателем, нужно придать смысл степени числа a с дробным показателем m/n , где m – целое число, а n - натуральное. Сделаем это.

Рассмотрим степень с дробным показателем вида . Чтобы сохраняло силу свойство степени в степени, должно выполняться равенство . Если учесть полученное равенство и то, как мы определили , то логично принять при условии, что при данных m , n и a выражение имеет смысл.

Несложно проверить, что при справедливы все свойства степени с целым показателем (это сделано в разделе свойства степени с рациональным показателем).

Приведенные рассуждения позволяют сделать следующий вывод : если при данных m , n и a выражение имеет смысл, то степенью числа a с дробным показателем m/n называют корень n -ой степени из a в степени m .

Это утверждение вплотную подводит нас к определению степени с дробным показателем. Остается лишь расписать, при каких m , n и a имеет смысл выражение . В зависимости от ограничений, накладываемых на m , n и a существуют два основных подхода.

Проще всего наложить ограничение на a , приняв a≥0 для положительных m и a>0 для отрицательных m (так как при m≤0 степень 0 m не определена). Тогда мы получаем следующее определение степени с дробным показателем.

Определение.

Степенью положительного числа a с дробным показателем m/n , где m – целое, а n – натуральное число, называется корень n -ой из числа a в степени m , то есть, .

Также определяется дробная степень нуля с той лишь оговоркой, что показатель должен быть положительным.

Определение.

Степень нуля с дробным положительным показателем m/n , где m – целое положительное, а n – натуральное число, определяется как .
При степень не определяется, то есть, степень числа нуль с дробным отрицательным показателем не имеет смысла.

Следует отметить, что при таком определении степени с дробным показателем существует один нюанс: при некоторых отрицательных a и некоторых m и n выражение имеет смысл, а мы отбросили эти случаи, введя условие a≥0 . Например, имеют смысл записи или , а данное выше определение заставляет нас говорить, что степени с дробным показателем вида не имеют смысла, так как основание не должно быть отрицательным.

Другой подход к определению степени с дробным показателем m/n заключается в раздельном рассмотрении четных и нечетных показателях корня . Этот подход требует дополнительного условия: степень числа a , показателем которой является , считается степенью числа a , показателем которой является соответствующая несократимая дробь (важность этого условия поясним чуть ниже). То есть, если m/n – несократимая дробь, то для любого натурального числа k степень предварительно заменяется на .

При четных n и положительных m выражение имеет смысл при любом неотрицательном a (корень четной степени из отрицательного числа не имеет смысла), при отрицательных m число a должно быть еще отличным от нуля (иначе будет деление на нуль). А при нечетных n и положительных m число a может быть любым (корень нечетной степени определен для любого действительного числа), а при отрицательных m число a должно быть отличным от нуля (чтобы не было деления на нуль).

Приведенные рассуждения приводят нас к такому определению степени с дробным показателем.

Определение.

Пусть m/n – несократимая дробь, m – целое, а n – натуральное число. Для любой сократимой обыкновенной дроби степень заменяется на . Степень числа a с несократимым дробным показателем m/n - это для



Поясним, зачем степень с сократимым дробным показателем предварительно заменяется степенью с несократимым показателем. Если бы мы просто определили степень как , и не оговорились о несократимости дроби m/n , то мы бы столкнулись с ситуациями, подобными следующей: так как 6/10=3/5 , то должно выполняться равенство , но , а .

Начальный уровень

Степень и ее свойства. Исчерпывающий гид (2019)

Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?

Чтобы узнать все о степенях, о том для чего они нужны, как использовать свои знания в повседневной жизни читай эту статью.

И, конечно же, знание степеней приблизит тебя к успешной сдаче ОГЭ или ЕГЭ и к поступлению в ВУЗ твоей мечты.

Let"s go... (Поехали!)

Важное замечание! Если вместо формул ты видишь абракадабру, почисти кэш. Для этого нужно нажать CTRL+F5 (на Windows) или Cmd+R (на Mac).

НАЧАЛЬНЫЙ УРОВЕНЬ

Возведение в степень - это такая же математическая операция, как сложение, вычитание, умножение или деление.

Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи.

Начнем со сложения.

Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно - 16 бутылок.

Теперь умножение.

Тот же самый пример с колой можно записать по-другому: . Математики - люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать». В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением. Согласись, считается легче и быстрее, чем.

Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения . Ты, конечно, можешь делать все медленнее, труднее и с ошибками! Но…

Вот таблица умножения. Повторяй.

И другой, красивее:

А какие еще хитрые приемы счета придумали ленивые математики? Правильно -возведение числа в степень .

Возведение числа в степень

Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень. Например, . Математики помнят, что два в пятой степени - это. И решают такие задачки в уме - быстрее, легче и без ошибок.

Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел . Поверь, это сильно облегчит тебе жизнь.

Кстати, почему вторую степень называют квадратом числа, а третью - кубом ? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.

Пример из жизни №1

Начнем с квадрата или со второй степени числа.

Представь себе квадратный бассейн размером метра на метра. Бассейн стоит у тебя на даче. Жара и очень хочется купаться. Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна.

Ты можешь просто посчитать, тыкая пальцем, что дно бассейна состоит из кубиков метр на метр. Если у тебя плитка метр на метр, тебе нужно будет кусков. Это легко… Но где ты видел такую плитку? Плитка скорее будет см на см. И тогда «пальцем считать» замучаешься. Тогда придется умножать. Итак, по одной стороне дна бассейна у нас поместится плиток (штук) и по другой тоже плиток. Умножив на, ты получишь плиток ().

Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Что это значит? Раз умножается одно и то же число, мы можем воспользоваться приемом «возведение в степень». (Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше. Для ЕГЭ это очень важно).
Итак, тридцать во второй степени будет (). Или же можно сказать, что тридцать в квадрате будет. Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат - это ВСЕГДА вторая степень какого-то числа. Квадрат - это изображение второй степени числа.

Пример из жизни №2

Вот тебе задание, посчитать, сколько квадратов на шахматной доске с помощью квадрата числа... По одной стороне клеток и по другой тоже. Чтобы посчитать их количество, нужно восемь умножить на восемь или… если заметить, что шахматная доска - это квадрат со стороной, то можно возвести восемь в квадрат. Получится клетки. () Так?

Пример из жизни №3

Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. (Объемы и жидкости, кстати, измеряются в кубических метрах. Неожиданно, правда?) Нарисуй бассейн: дно размером на метра и глубиной метра и попробуй посчитать, сколько всего кубов размером метр на метр войдет в твой бассейн.

Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Не сбился? Трудно пальцем считать? Так-то! Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту. В нашем случае объем бассейна будет равен кубов… Легче правда?

А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя… А что это значит? Это значит, что можно воспользоваться степенью. Итак, то, что ты раз считал пальцем, они делают в одно действие: три в кубе равно. Записывается это так: .

Остается только запомнить таблицу степеней . Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки - можешь продолжать считать пальцем.

Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни.

Пример из жизни №4

У тебя есть миллиона рублей. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Сколько денег у тебя будет через лет? Если ты сейчас сидишь и «считаешь пальцем», значит ты очень трудолюбивый человек и.. глупый. Но скорее всего ты дашь ответ через пару секунд, потому что ты - умный! Итак, в первый год - два умножить на два… во второй год - то, что получилось, еще на два, в третий год… Стоп! Ты заметил, что число перемножается само на себя раз. Значит, два в пятой степени - миллиона! А теперь представь, что у вас соревнование и эти миллиона получит тот, кто быстрее посчитает… Стоит запомнить степени чисел, как считаешь?

Пример из жизни №5

У тебя есть миллиона. В начале каждого года ты зарабатываешь на каждом миллионе еще два. Здорово правда? Каждый миллион утраивается. Сколько денег у тебя будет через года? Давай считать. Первый год - умножить на, потом результат еще на … Уже скучно, потому что ты уже все понял: три умножается само на себя раза. Значит в четвертой степени равно миллион. Надо просто помнить, что три в четвертой степени это или.

Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них.

Термины и понятия... чтобы не запутаться

Итак, для начала давай определим понятия. Как думаешь, что такое показатель степени ? Это очень просто - это то число, которое находится «вверху» степени числа. Не научно, зато понятно и легко запомнить…

Ну и заодно, что такое основание степени ? Еще проще - это то число, которое находится внизу, в основании.

Вот тебе рисунок для верности.

Ну и в общем виде, чтобы обобщить и лучше запомнить… Степень с основанием « » и показателем « » читается как « в степени » и записывается следующим образом:

Степень числа с натуральным показателем

Ты уже наверное, догадался: потому что показатель степени - это натуральное число. Да, но что такое натуральное число ? Элементарно! Натуральные это те числа, которые используются в счете при перечислении предметов: один, два, три… Мы же когда считаем предметы не говорим: «минус пять», «минус шесть», «минус семь». Мы так же не говорим: «одна третья», или «ноль целых, пять десятых». Это не натуральные числа. А какие это числа как ты думаешь?

Числа типа «минус пять», «минус шесть», «минус семь» относятся к целым числам. Вообще, к целым числам относятся все натуральные числа, числа противоположные натуральным (то есть взятые со знаком минус), и число. Ноль понять легко - это когда ничего нет. А что означают отрицательные («минусовые») числа? А вот их придумали в первую очередь для обозначения долгов: если у тебя баланс на телефоне рублей, это значит, что ты должен оператору рублей.

Всякие дроби - это рациональные числа. Как они возникли, как думаешь? Очень просто. Несколько тысяч лет назад наши предки обнаружили, что им не хватает натуральных чисел для измерения длинны, веса, площади и т.п. И они придумали рациональные числа … Интересно, правда ведь?

Есть еще иррациональные числа. Что это за числа? Если коротко, то бесконечная десятичная дробь. Например, если длину окружности разделить на ее диаметр, то в получится иррациональное число.

Резюме:

Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).

1. Любое число в первой степени равно самому себе:
2. Возвести число в квадрат — значит умножить его само на себя:
3. Возвести число в куб — значит умножить его само на себя три раза:

Определение. Возвести число в натуральную степень — значит умножить число само на себя раз:
.

Свойства степеней

Откуда эти свойства взялись? Сейчас покажу.

Посмотрим: что такое и ?

По определению:

Сколько здесь множителей всего?

Очень просто: к множителям мы дописали множителей, итого получилось множителей.

Но по определению это степень числа с показателем, то есть: , что и требовалось доказать.

Пример : Упростите выражение.

Решение:

Пример: Упростите выражение.

Решение: Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания!
Поэтому степени с основанием мы объединяем, а остается отдельным множителем:

только для произведения степеней!

Ни в коем случае нельзя написать, что.

2. то и есть -ая степень числа

Так же, как и с предыдущим свойством, обратимся к определению степени:

Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -ая степень числа:

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме:

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать?

Но это неверно, ведь.

Степень с отрицательным основанием

До этого момента мы обсуждали только то, каким должен быть показатель степени.

Но каким должно быть основание?

В степенях с натуральным показателем основание может быть любым числом . И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже.

Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?

Например, положительным или отрицательным будет число? А? ? С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.

Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на, получится.

Определи самостоятельно, какой знак будут иметь следующие выражения:

1)	2)	3)
4)	5)	6)

Справился?

Вот ответы: В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание - степень четная, а значит, результат всегда будет положительным.

Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).

Пример 6) уже не так прост!

6 примеров для тренировки

Разбор решения 6 примеров

Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно - разность квадратов! Получаем:

Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило.

Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.

Но важно запомнить: меняются все знаки одновременно !

Вернемся к примеру:

И снова формула:

Целыми мы называем натуральные числа, противоположные им (то есть взятые со знаком « ») и число.

целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.

А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного.

Любое число в нулевой степени равно единице :

Как всегда, зададимся вопросом: почему это так?

Рассмотрим какую-нибудь степень с основанием. Возьмем, например, и домножим на:

Итак, мы умножили число на, и получили то же, что и было - . А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на. Значит.

Можем проделать то же самое уже с произвольным числом:

Повторим правило:

Любое число в нулевой степени равно единице.

Но из многих правил есть исключения. И здесь оно тоже есть - это число (в качестве основания).

С одной стороны, в любой степени должен равняться - сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, как и любое число в нулевой степени, должен равняться. Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.

Поехали дальше. Кроме натуральных чисел и числа к целым относятся отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:

Отсюда уже несложно выразить искомое:

Теперь распространим полученное правило на произвольную степень:

Итак, сформулируем правило:

Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: (т.к. на делить нельзя).

Подведем итоги:

I. Выражение не определено в случае. Если, то.

II. Любое число в нулевой степени равно единице: .

III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: .

Задачи для самостоятельного решения:

Ну и, как обычно, примеры для самостоятельного решения:

Разбор задач для самостоятельного решения:

Знаю-знаю, числа страшные, но на ЕГЭ надо быть готовым ко всему! Реши эти примеры или разбери их решение, если не смог решить и ты научишься легко справляться с ними на экзамене!

Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.

Теперь рассмотрим рациональные числа. Какие числа называются рациональными?

Ответ: все, которые можно представить в виде дроби, где и - целые числа, причем.

Чтобы понять, что такое «дробная степень» , рассмотрим дробь:

Возведем обе части уравнения в степень:

Теперь вспомним правило про «степень в степени» :

Какое число надо возвести в степень, чтобы получить?

Эта формулировка - определение корня -ой степени.

Напомню: корнем -ой степени числа () называется число, которое при возведении в степень равно.

То есть, корень -ой степени - это операция, обратная возведению в степень: .

Получается, что. Очевидно, этот частный случай можно расширить: .

Теперь добавляем числитель: что такое? Ответ легко получить с помощью правила «степень в степени»:

Но может ли основание быть любым числом? Ведь корень можно извлекать не из всех чисел.

Никакое!

Вспоминаем правило: любое число, возведенное в четную степень - число положительное. То есть, извлекать корни четной степени из отрицательных чисел нельзя!

А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.

А что насчет выражения?

Но тут возникает проблема.

Число можно представить в виде дргих, сократимых дробей, например, или.

И получается, что существует, но не существует, а ведь это просто две разные записи одного и того же числа.

Или другой пример: раз, то можно записать. Но стоит нам по-другому записать показатель, и снова получим неприятность: (то есть, получили совсем другой результат!).

Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем .

Итак, если:

• — натуральное число;
• — целое число;

Примеры:

Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:

5 примеров для тренировки

Разбор 5 примеров для тренировки

Ну а теперь - самое сложное. Сейчас мы разберем степень с иррациональным показателем .

Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением

Ведь по определению иррациональные числа - это числа, которые невозможно представить в виде дроби, где и - целые числа (то есть, иррациональные числа - это все действительные числа кроме рациональных).

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.

Например, степень с натуральным показателем - это число, несколько раз умноженное само на себя;

...число в нулевой степени - это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось - поэтому результатом является только некая «заготовка числа», а именно число;

...степень с целым отрицательным показателем - это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель - это даже не действительное число.

Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

КУДА МЫ УВЕРЕНЫ ТЫ ПОСТУПИШЬ! (если научишься решать такие примеры:))

Например:

Реши самостоятельно:

Разбор решений:

1. Начнем с уже обычного для нас правила возведения степени в степень:

Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:

В данном случае,

Получается, что:

Ответ: .

2. Приводим дроби в показателях степеней к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например:

Ответ: 16

3. Ничего особенного, применяем обычные свойства степеней:

ПРОДВИНУТЫЙ УРОВЕНЬ

Определение степени

Степенью называется выражение вида: , где:

• — основание степени;
• — показатель степени.

Степень с натуральным показателем {n = 1, 2, 3,...}

Возвести число в натуральную степень n — значит умножить число само на себя раз:

Степень с целым показателем {0, ±1, ±2,...}

Если показателем степени является целое положительное число:

Возведение в нулевую степень :

Выражение неопределенное, т.к., с одной стороны, в любой степени - это, а с другой - любое число в -ой степени - это.

Если показателем степени является целое отрицательное число:

(т.к. на делить нельзя).

Еще раз о нулях: выражение не определено в случае. Если, то.

Примеры:

Степень с рациональным показателем

• — натуральное число;
• — целое число;

Примеры:

Свойства степеней

Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.

Посмотрим: что такое и?

По определению:

Итак, в правой части этого выражения получается такое произведение:

Но по определению это степень числа с показателем, то есть:

Что и требовалось доказать.

Пример : Упростите выражение.

Решение : .

Пример : Упростите выражение.

Решение : Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием мы объединяем, а остается отдельным множителем:

Еще одно важное замечание: это правило - только для произведения степеней !

Ни в коем случае нелья написать, что.

Так же, как и с предыдущим свойством, обратимся к определению степени:

Перегруппируем это произведение так:

Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -я степень числа:

По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: !

Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать? Но это неверно, ведь.

Степень с отрицательным основанием.

До этого момента мы обсуждали только то, каким должен быть показатель степени. Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом .

И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?

Например, положительным или отрицательным будет число? А? ?

С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.

Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на (), получится - .

И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:

1. четную степень, - число положительное .
2. Отрицательное число, возведенное в нечетную степень, - число отрицательное .
3. Положительное число в любой степени - число положительное.
4. Ноль в любой степени равен нулю.

Определи самостоятельно, какой знак будут иметь следующие выражения:

1.	2.	3.
4.	5.	6.

Справился? Вот ответы:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.

В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание - степень четная, а значит, результат всегда будет положительным. Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).

Пример 6) уже не так прост. Тут нужно узнать, что меньше: или? Если вспомнить, что, становится ясно, что, а значит, основание меньше нуля. То есть, применяем правило 2: результат будет отрицательным.

И снова используем определение степени:

Все как обычно - записываем определение степеней и, делим их друг на друга, разбиваем на пары и получаем:

Прежде чем разобрать последнее правило, решим несколько примеров.

Вычисли значения выражений:

Решения :

Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно - разность квадратов!

Получаем:

Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило 3. Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.

Если домножить его на, ничего не поменяется, верно? Но теперь получается следующее:

Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках. Но важно запомнить: меняются все знаки одновременно! Нельзя заменить на, изменив только один неугодный нам минус!

Вернемся к примеру:

И снова формула:

Итак, теперь последнее правило:

Как будем доказывать? Конечно, как обычно: раскроем понятие степени и упростим:

Ну а теперь раскроем скобки. Сколько всего получится букв? раз по множителей - что это напоминает? Это не что иное, как определение операции умножения : всего там оказалось множителей. То есть, это, по определению, степень числа с показателем:

Пример:

Степень с иррациональным показателем

В дополнение к информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением - ведь по определению иррациональные числа - это числа, которые невозможно представить в виде дроби, где и - целые числа (то есть, иррациональные числа - это все действительные числа, кроме рациональных).

При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах. Например, степень с натуральным показателем - это число, несколько раз умноженное само на себя; число в нулевой степени - это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось - поэтому результатом является только некая «заготовка числа», а именно число; степень с целым отрицательным показателем - это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.

Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.

Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель - это даже не действительное число. Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.

Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)

Например:

Реши самостоятельно:

1)

2)

3)

Ответы:

1. Вспоминаем формулу разность квадратов. Ответ: .
2. Приводим дроби к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например: .
3. Ничего особенного, применяем обычные свойства степеней:

КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ

Степенью называется выражение вида: , где:

Степень с целым показателем

степень, показатель которой — натуральное число (т.е. целое и положительное).

Степень с рациональным показателем

степень, показатель которой — отрицательные и дробные числа.

Степень с иррациональным показателем

степень, показатель которой — бесконечная десятичная дробь или корень.

Свойства степеней

Особенности степеней.

• Отрицательное число, возведенное в четную степень, - число положительное .
• Отрицательное число, возведенное в нечетную степень, - число отрицательное .
• Положительное число в любой степени - число положительное.
• Ноль в любой степени равен.
• Любое число в нулевой степени равно.

ТЕПЕРЬ ТЕБЕ СЛОВО...

Как тебе статья? Напиши внизу в комментариях понравилась или нет.

Расскажи о своем опыте использования свойств степеней.

Возможно у тебя есть вопросы. Или предложения.

Напиши в комментариях.

И удачи на экзаменах!

- приветствие;

Класс делится на 2 группыпо 3-4 чел. Состав учащихся различный по уровню знаний. На столах3 карточки.

Д/З(презентации)

Графический диктант

Решение задач

1)Графический диктант.

2.Образующая конуса L наклонена к плоскости основания под углом в 300. Найдите высоту. Ответ: 2L.

4.В прямоугольном треугольнике АВС, (рисунок 3), В = 600, ВС = 1. Найдите длину катета АС, используя теорему Пифагора.

5.MNK прямоугольный (рисунок 4), К = 450, катет KN = 8. Найдите длину катета MN.

Ключ: __ __ __ __.

Заполнение опорных листочков.

Цилиндр

Конус

Усеченный конус

l -
h -.
r -.
Sполн. =

l -
h -
r -
S полн. =
V =

r -
r1 -
h -
l -
Sполн =
V =

Цилиндр , Конус, Усеченный конус

Мотивация. « Тяжело в учении, легко на ЕНТ»

4.Изучение нового материала: (слайды).

Элементы цилиндра; R, L,H,D

1. Определение конуса.

Элементы конуса-R, L,H,D.

5.Закрепление.

Задача 1.

1 м3 щебня весит 3 т. На один воз грузят 0,5 т.

Дано: конус, (рисунок 5)

ОА = 2м,
АР = 3,5м,
1м3 = 3т,
1 воз = 0,5 т.

Рисунок 5

Найти: количество возов.

Решение: V =

Найдем высоту:

h =м м, тогда
V = = 12 м3,
12м3 . 3 т = 36 т в одной куче щебня,
36: 0,5 = 72 воза потребуется.

Ответ: 72 воза.

2)Задача №7-стр57

основания

поверхности

поверхности

элементы

Усечённый конус

Карточка №3.

ИНСТРУКЦИЯ.

Время выполнения 5-7 минут

Старайтесь решать сами!

лидеру группы. НЕ БОЛЕЕ ТРЕХ РАЗ.

Просмотр содержимого документа
«Поурочный план на тему "11-геометрия.Объём цилиндра, конуса и усечённого конуса" . »

Жамбылский обл.Кордайский район. с. Кайнар

Сш № 32 им. В.В.Маяковского

Учитель математики Дурсунова Б.О.

Урок№25 /4 Геометрия 11 класс.

Тема. «Объём цилиндра, конуса и усечённого конуса»

Цели урока:

Создать условия для продуктивного изучения теоремы об объёме цилиндра, конуса и усечённого конуса, и выработки умений решения задач с использованием формул объёма этого тела;

Способствовать развитию наблюдательности, умения сравнивать, выдвигать гипотезы, делать выводы;

Воспитание познавательной активности, самостоятельности, упорства при достижении цели.

Тип урока : комбинированный с использованием ИКТ.

Оборудовани е: интерактивная доска, презентации детей, модели фигур, таблицы, учебники, тетради, чертёжные принадлежности.

Формы общения : групповая, индивидуальная.

Ход урока

Организационный момент.

- приветствие;

- проверка подготовленности к уроку;

- постановка целей урока и плана проведения.

Класс делится на 2 группы по 3-4 чел. Состав учащихся различный по уровню знаний. На столах 3 карточки.

Карточка №1. Учет деятельности учащихся.

	Д/З(презентации)	Графический диктант	Решение задач

Учащиеся коллективно выставляют оценку каждому. В конце урока подводят итог.

2.Проверка домашнего задания.

1)Графический диктант.

Ответьте на вопросы. Если вы согласны с ответом или утверждением, то поставьте “__”, иначе “ ”. Первому, правильно выполнившему все задания, оценка ставиться в журнал. Все остальные сдают листочки с ответами на проверку.

1.Радиус основания конуса 3 м, высота 4 м. Найдите образующую. Ответ: 5 м.

2.Образующая конуса L наклонена к плоскости основания под углом в 30 0 . Найдите высоту. Ответ: 2L.

3.Развертка конуса состоит из треугольника и круга.

4.В прямоугольном треугольнике АВС, (рисунок 3), В = 60 0 , ВС = 1. Найдите длину катета АС, используя теорему Пифагора.

5.MNK прямоугольный (рисунок 4), К = 45 0 , катет KN = 8. Найдите длину катета MN.

6.Высота конуса равна 6, радиус основания равен 8. Найдите боковую поверхность. Ответ: 80.

7.Радиус оснований усеченного конуса 3м и 6 м, высота 4 м. Найдите образующую. Ответ 5 м.

Ключ: __ __ __ __.

2). Повторение основных сведений

Заполнение опорных листочков. Заранее раздается каждому ученику листочек.

Цилиндр	Конус	Усеченный конус
l – h –. r –. S полн. =	l – h – r – S полн. = V =	r – r 1 – h – l – Sполн = V =

Просмотр презентаций учащихся на тему: Цилиндр , Конус, Усеченный конус

3.Сообщение темы, цели урока.

Мотивация. « Тяжело в учении, легко на ЕНТ»

4.Изучение нового материала: (слайды).

1.Определение цилиндрической поверхности;

Элементы цилиндра; R, L,H,D

Теорема об объёме прямой призмы; V=S H

Вписанный в призму цилиндр и описанный цилиндр около призмы;

Изучение теоремы об объёме цилиндра. V=nR²H

Определение конуса.

Элементы конуса-R, L,H,D.

Теорема об объёме пирамиды.V=1/3*SH

Вписанный в пирамиду конус и описанный конус около пирамиды;

Изучение теоремы об объёме конуса.V=1/3*nR²H

5.Закрепление.

Задача 1. Куча щебня имеет коническую форму, радиус основания которой 2 м и образующая 3,5 м. Сколько надо возов, чтобы перевезти щебень, уложенный в кучу?

1 м 3 щебня весит 3 т. На один воз грузят 0,5 т.

Дано: конус, (рисунок 5)

ОА = 2м,
АР = 3,5м,
1м 3 = 3т,
1 воз = 0,5 т.

Рисунок 5

Найти: количество возов.

Решение: V =

Найдем высоту:

h =м м, тогда
V = = 12 м 3 ,
12м 3 3 т = 36 т в одной куче щебня,
36: 0,5 = 72 воза потребуется.

Ответ: 72 воза.

2)Задача №7-стр57

Карточка №2. Заполнить каждому ученику:

	основания	поверхности	поверхности		элементы
Усечённый конус

Карточка №3.

ИНСТРУКЦИЯ.

Время выполнения 5-7 минут

Перед вами три задачи, расположенные в порядке возрастания сложности.

Решив только первую задачу, вы получаете оценку «3».

Решив первую и вторую задачи, вы получите оценку «4».

Решив все три задачи, вы получите оценку «5».

Старайтесь решать сами!

В случае затруднения, вы можете обратиться за помощью к лидеру группы. За данной помощью, вы можете обратиться НЕ БОЛЕЕ ТРЕХ РАЗ .

1 группа-1. В цилиндрический сосуд налили 3000 куб см воды. Уровень воды при этом достиг высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 3см. Чему равен объем детали?

2. Цилиндр и конус имеют общее основание и высоту. Вычислите объем цилиндра, если объем конуса равен 21.

3. Высота конуса равна 12см, а диаметр основания 10см.Найдите площадь полной поверхности и объем конуса.

2 группа.- 1. Высота конуса равна 15см, а диаметр основания 16см. Найдите площадь полной поверхности и объем конуса.

2. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем конуса, если объем цилиндра равен 60куб см.

3. В цилиндрический сосуд налили 2900куб см воды. Уровень воды при этом достиг высоты 20см, В жидкость полностью погрузили деталь. При этом уровень воды в сосуде поднялся на 15см. Чему равен объем детали?

Ответы: 1-450куб см, 63, 90п и 100п.

2-200п и 320п, 20, 2175куб см.

5.-Выразить величину из формулы: Называется формула объема цилиндра, объема конуса. Выразить высоту, радиус, образующую. группы записывают фломастером на альбомном листе и вывешивают на доске. Какая группа быстрее и правильно запишет.

6.-Что общего у цилиндра и валика для покраски, конуса и картиной Шишкина «Утро в сосновом бору». (С древне греческого: цилиндр-валик, конус- сосновая шишка).

6.Домашнее задание: Тест по данной теме. Задания из ЕНТ.

7. Итог урока подвести по карточке учета. После проверки задачи в тетрадях выставить общую оценку в журнал.

МБОУ СОШ №42

Урок геометрии в 11 «А» классе.

Тема: «Объем цилиндра. Объем конуса».

Учитель математики

Балаева Б. М.

Владикавказ

2012г

Тема: «Объем цилиндра. Объем конуса»

(1 слайд)

Цель : совершенствовать навыки решения задач на нахождение объемов фигур

вращения (цилиндра и конуса), подготовка к ЕГЭ.

Задачи : - способствовать актуализации полученных знаний по теме;

Способствовать развитию умений переносить знания в нестандартные

ситуации;

Совершенствовать информационную компетенцию через анализ данных

задач и построение алгоритма решения;

Создать условия для воспитания коммуникативных навыков, через

организацию работы в микро группах.

Оборудование : интерактивная доска, карточки-задания для работы в микро-

группах.

Формы и методы работы : индивидуальная, фронтальная, работа в малых

группах; анализ, сравнение, презентация.

Ход урока.

Организационный момент .

Проверка готовности к уроку обучающихся: наличие учебников, рабочих тетрадей, выполнение домашней работы, в том числе индивидуальной.

Объявление темы урока, мотивация.

Учитель: «Данный урок – продолжение серии уроков по решению задач, связанных с фигурами вращения. Имея навыки работы с опорными задачами, необходимо научиться решать комбинационные задачи, применяя уже полученные знания в нестандартных ситуациях».

Обучающиеся формулируют определения и свойства фигур, значение которых должно привести к достижению поставленной цели:

Актуализировать уже изученный теоретический материал;

Вспомнить основные части фигур: цилиндра и конуса; (2 – 4 слайды)

Повторить основные формулы нахождения площади основания,

боковой поверхности; всей поверхности цилиндра и конуса;

Закрепить формулы нахождения объемов;(5 слайд)

Использовать правила работы в микро группах для интенсификации учебной

деятельности.

Актуализация и коррекция опорных знаний.

А) Представление индивидуального домашнего задания – презентация по теме «Цилиндр»

Б) Фронтальная устная работа: заполнить первый контрольный столбец таблицы

В) Представление индивидуального домашнего задания – презентация по теме «Конус» (фронтальная устная работа)

Г) Индивидуальная письменная работа – заполнить второй контрольный столбец таблицы

(6 слайд)

Таблица 1.

Основные понятия по теме «Цилиндр и конус»

Характеристика

Цилиндр

Конус

Образующая фигура

прямоугольник

прямоугольный треугольник

2.

Основные линии фигуры

высота (образующая), радиус основания, ось

высота, образующая, радиус основания,

ось

3.

Вид развертки основания

круг

круг

4.

Вид развертки боковой поверхности

прямоугольник

круговой сектор

5.

Сечения

прямоугольники, окружности

треугольники, окружности, эллипсы

6.

Формула площади боковой поверхности

S = 2 π Rh

S = πRl

7.

Формула площади полной поверхности

S = 2 π R(h+R)

S = π R(R+l)

8.

Формула объема фигуры

V = πR 2 h

V = S осн. h

V = ⅓ S осн. h

V = ⅓ πR 2 h

Мини – игра «Цилиндр».

Предметы, имеющие более или менее точную форму цилиндра, а также и такие, у которых детали цилиндрической формы, встречаются повсеместно: в быту, в строительстве, в технике – играют важную роль.

Назовите как можно больше предметов, имеющих цилиндрическую форму.

(7 – 17 слайды)

Каждый учащийся записывает предметы на листочках и передает на первую парту.

Учащиеся, сидящие за первой партой каждого ряда, по очереди зачитывают слова

Тестирование по теме :

«Опорные задачи для цилиндра и конуса».

Раздается каждому ряду условия задач и дается время. Исправления не допускаются.

(18 слайд)

1. Диаметр основания цилиндра 4 см, высота 3 см. Найти диагональ осевого сечения.

А ) 5 см В) 4 см С) 6 см

2. Если увеличить радиус основания цилиндра в 2 раза, то во сколько раз увеличиться его объем?

А) 2 В) 3 С ) 4

3. Высота цилиндра 2 см., радиус основания 3 см. Определить объем.

А) 18 π см 3 В) 1,8 π см 3 С) 20π см 3

4. Высота конуса 4 см, радиус основания 3 см. Найти образующую конуса.

А) 7 см В ) 5 см С) 6 см

5. Высота конуса 12 см, образующая 13 см. Найти боковую поверхность конуса.

А) 25 π см 2 В) 63 π см 2 С) 65π см 2

6. Найти объем тела, полученного вращением прямоугольного треугольника с катетами 3 см и 4 см вокруг меньшего катета.

А) 18 π см 3 В) 16 π см 3 С) 20π см 3

Учитель в устной форме проверяет правильность ответов.

Применение знаний для решения заданий части В: В9 и В11.

(19 -20 слайды)

Самостоятельная работа по решению задач (используется «Сборник задач для подготовки к ЕГЭ 2012» под ред. Семенова А. Л., Ященко И. В. - М:Национальное образование, 2011):

1. Высота конуса равна 8, а диаметр основания – 30. Найти образующую конуса.(В9 вариант 6 .отв.17)

2. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 21. (В11 вариант 13. Отв.63)

3. Объем конуса равен 40. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найти объем меньшего конуса. (В11 вариант 17. Отв.8)

4. Площадь боковой поверхности цилиндра равна 14π, а диаметр основания равен 2. Найти высоту цилиндра. (вариант 28 В9. Отв.7)

(21 слайд)

Рефлексия

1.Удовлетворены ли вы работой своей микро группы?

2.Хотели бы Вы перейти в другую микро группу?

3.Испытываете ли Вы чувство благодарности к кому-то из представителей Вашей группы?

4.Считаете ли Вы свою работу на уроке полезной для Вашей микро группы?

5.Можете ли Вы сказать, что в ходе урока произошло обогащение запаса Ваших знаний?

6.Вы готовы сформулировать вопросы, которые возникли в ходе урока и на которые Вы не получили ответа?

7.Хотели бы Вы получить оценку вашей работы на уроке?

1. Если у Вас лидируют ответы «да», то вы хорошо поработали как индивидуально, так и в команде.

2. А если больше ответов «нет», то выводы таковы:

знания необходимо пополнять;

нужно принимать более активное участие на каждом уроке;

систематически выполнять домашнее задание…

Выставление отметок в журнал.

Инструктаж по выполнению домашнего задания.

(22 слайд)

Задание: теория – п. 76 стр.122

Задачи - №16, №19 (стр. 129)

(23 слайд)

Обоснование: не рассмотрены задачи на нахождение объема усеченного конуса.

Та команда (ряд), которая активней участвовала и находила верные ответы, освобождается от домашнего задания!

Спасибо за урок, ребята! (23 слайд)

Тела вращения, изучаемые в школе, - это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы - считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, - снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто - рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.