И т. п. объектов , которые характеризуются конечным набором некоторых свойств и признаков. Такие задачи решаются довольно часто, например, при переходе или проезде улицы по сигналам светофора. Распознавание цвета загоревшейся лампы светофора и знание правил дорожного движения позволяет принять правильное решение о том, можно или нельзя переходить улицу.

Необходимость в таком распознавании возникает в самых разных областях - от военного дела и систем безопасности до оцифровки аналоговых сигналов.

Проблема распознавания образа приобрела выдающееся значение в условиях информационных перегрузок, когда человек не справляется с линейно-последовательным пониманием поступающих к нему сообщений, в результате чего его мозг переключается на режим одновременности восприятия и мышления, которому такое распознавание свойственно.

Неслучайно, таким образом, проблема распознавания образа оказалась в поле междисциплинарных исследований - в том числе в связи с работой по созданию искусственного интеллекта , а создание технических систем распознавания образа привлекает к себе всё большее внимание.

Энциклопедичный YouTube

1 / 4

Введение в распознавание образов

Р.В. Шамин. Лекция № 6 Сети Хопфилда и Хемминга в задачах распознавания образов

[ДДШ-2016]: Нейронные сети и современное компьютерное зрение

Лекция 9. Экспоненциальное сглаживание. Распознавание образов: метод к-го ближайшего соседа

Субтитры

Направления в распознавании образов

Можно выделить два основных направления :

Изучение способностей к распознаванию, которыми обладают живые существа, объяснение и моделирование их;
Развитие теории и методов построения устройств, предназначенных для решения отдельных задач в прикладных целях.

Формальная постановка задачи

Распознавание образов - это отнесение исходных данных к определенному классу с помощью выделения существенных признаков, характеризующих эти данные, из общей массы несущественных данных.

При постановке задач распознавания стараются пользоваться математическим языком, стремясь - в отличие от теории искусственных нейронных сетей , где основой является получение результата путём эксперимента, - заменить эксперимент логическими рассуждениями и математическими доказательствами .

Классическая постановка задачи распознавания образов : Дано множество объектов. Относительно них необходимо провести классификацию. Множество представлено подмножествами, которые называются классами. Заданы: информация о классах, описание всего множества и описание информации об объекте, принадлежность которого к определенному классу неизвестна. Требуется по имеющейся информации о классах и описании объекта установить - к какому классу относится этот объект.

Наиболее часто в задачах распознавания образов рассматриваются монохромные изображения , что дает возможность рассматривать изображение как функцию на плоскости. Если рассмотреть точечное множество на плоскости T {\displaystyle T} , где функция выражает в каждой точке изображения его характеристику - яркость, прозрачность, оптическую плотность, то такая функция есть формальная запись изображения.

Множество же всех возможных функций f (x , y) {\displaystyle f(x,y)} на плоскости T {\displaystyle T} - есть модель множества всех изображений X {\displaystyle X} . Вводя понятие сходства между образами можно поставить задачу распознавания. Конкретный вид такой постановки сильно зависит от последующих этапов при распознавании в соответствии с тем или иным подходом.

Некоторые методы распознавания графических образов

Для оптического распознавания образов можно применить метод перебора вида объекта под различными углами, масштабами, смещениями и т. д. Для букв нужно перебирать шрифт, свойства шрифта и т. д.

Второй подход - найти контур объекта и исследовать его свойства (связность, наличие углов и т. д.)

Ещё один подход - использовать искусственные нейронные сети . Этот метод требует либо большого количества примеров задачи распознавания (с правильными ответами), либо специальной структуры нейронной сети, учитывающей специфику данной задачи.

Персептрон как метод распознавания образов

Ф. Розенблатт, вводя понятие о модели мозга , задача которой состоит в том, чтобы показать, как в некоторой физической системе, структура и функциональные свойства которой известны, могут возникать психологические явления, описал простейшие эксперименты по различению. Данные эксперименты целиком относятся к методам распознавания образов, но отличаются тем, что алгоритм решения не детерминированный.

Простейший эксперимент, на основе которого можно получить психологически значимую информацию о некоторой системе, сводится к тому, что модели предъявляются два различных стимула и требуется, чтобы она реагировала на них различным образом. Целью такого эксперимента может быть исследование возможности их спонтанного различения системой при отсутствии вмешательства со стороны экспериментатора, или, наоборот, изучение принудительного различения, при котором экспериментатор стремится обучить систему проводить требуемую классификацию.

В опыте с обучением персептрону обычно предъявляется некоторая последовательность образов, в которую входят представители каждого из классов, подлежащих различению. В соответствии с некоторым правилом модификации памяти правильный выбор реакции подкрепляется. Затем персептрону предъявляется контрольный стимул и определяется вероятность получения правильной реакции для стимулов данного класса. В зависимости от того, совпадает или не совпадает выбранный контрольный стимул с одним из образов, которые использовались в обучающей последовательности, получают различные результаты:

Если контрольный стимул не совпадает ни с одним из обучающих стимулов, то эксперимент связан не только с чистым различением , но включает в себя и элементы обобщения .
Если контрольный стимул возбуждает некоторый набор сенсорных элементов, совершенно отличных от тех элементов, которые активизировались при воздействии ранее предъявленных стимулов того же класса, то эксперимент является исследованием чистого обобщения .

Персептроны не обладают способностью к чистому обобщению, но они вполне удовлетворительно функционируют в экспериментах по различению, особенно если контрольный стимул достаточно близко совпадает с одним из образов, относительно которых персептрон уже накопил определенный опыт.

Примеры задач распознавания образов

Распознавание штрих-кодов
Распознавание автомобильных номеров
Распознавание изображений
Распознавание локальных участков земной коры, в которых находятся месторождения

Sun, Mar 29, 2015

В настоящее время существует множество задач, в которых требуется принять некоторое решение в зависимости от присутствия на изображении объекта или классифицировать его. Способность «распознавать» считается основным свойством биологических существ, в то время как компьютерные системы этим свойством в полной мере не обладают.

Рассмотрим общие элементы модели классификации.

Класс - множество объектом имеющие общие свойства. Для объектов одного класса предполагается наличие «схожести». Для задачи распознавания может быть определено произвольное количество классов, больше 1. Количество классов обозначается числом S. Каждый класс имеет свою идентифицирующую метку класса.

Классификация - процесс назначения меток класса объектам, согласно некоторому описанию свойств этих объектов. Классификатор - устройство, которое в качестве входных данных получает набор признаков объекта, а в качестве результата выдающий метку класса.

Верификация - процесс сопоставления экземпляра объекта с одной моделью объекта или описанием класса.

Под образом будем понимать наименование области в пространстве признаков, в которой отображается множество объектов или явлений материального мира. Признак - количественное описание того или иного свойства исследуемого предмета или явления.

Пространство признаков это N-мерное пространство, определенное для данной задачи распознавания, где N - фиксированное число измеряемых признаков для любых объектов. Вектор из пространства признаков x, соответствующий объекту задачи распознавания это N-мерный вектор с компонентами (x_1,x_2,…,x_N), которые являются значениями признаков для данного объекта.

Другими словами, распознавание образов можно определить, как отнесение исходных данных к определенному классу с помощью выделение существенных признаков или свойств, характеризующих эти данные, из общей массы несущественных деталей.

Примерами задач классификации являются:

распознавание символов;
распознавание речи;
установление медицинского диагноза;
прогноз погоды;
распознавание лиц
классификация документов и др.

Чаще всего исходным материалом служит полученное с камеры изображение. Задачу можно сформулировать как получение векторов признаков для каждого класса на рассматриваемом изображении. Процесс можно рассматривать как процесс кодирования, заключающийся в присвоении значения каждому признаку из пространства признаков для каждого класса.

Если рассмотреть 2 класса объектов: взрослые и дети. В качестве признаков можно выбрать рост и вес. Как следует из рисунка эти два класса образуют два непересекающихся множества, что можно объяснить выбранными признаками. Однако не всегда удается выбрать правильные измеряемые параметры в качестве признаков классов. Например выбранные параметры не подойдут для создания непересекающихся классов футболистов и баскетболистов.

Второй задачей распознавания является выделение характерных признаков или свойств из исходных изображений. Эту задачу можно отнести к предварительной обработке. Если рассмотреть задачу распознавания речи, можно выделить такие признаки как гласные и согласные звуки. Признак должен представлять из себя характерное свойство конкретного класса, при этом общие для этого класса. Признаки, характеризующие отличия между - межклассовые признаки. Признаки общие для всех классов не несут полезной информации и не рассматриваются как признаки в задаче распознавания. Выбор признаков является одной из важных задач, связанных с построением системы распознавания.

После того, как определены признаки необходимо определить оптимальную решающую процедуру для классификации. Рассмотрим систему распознавания образов, предназначенную для распознавания различных M классов, обозначенных как m_1,m_2,…,m3. Тогда можно считать, что пространство образов состоит из M областей, каждая содержит точки, соответствующие образом из одного класса. Тогда задача распознавания может рассматриваться как построение границ, разделяющих M классов, исходя из принятых векторов измерений.

Решение задачи предварительной обработки изображения, выделение признаков и задачи получения оптимального решения и классификации обычно связано с необходимостью произвести оценку ряда параметров. Это приводит к задаче оценки параметров. Кроме того, очевидно, что выделение признаков может использовать дополнительную информацию исходя из природы классов.

Сравнение объектов можно производить на основе их представления в виде векторов измерений. Данные измерений удобно представлять в виде вещественных чисел. Тогда сходство векторов признаков двух объектов может быть описано с помощью евклидова расстояния.

где d - размерность вектора признака.

Разделяют 3 группы методов распознавания образов:

Сравнение с образцом . В эту группу входит классификация по ближайшему среднему, классификация по расстоянию до ближайшего соседа. Также в группу сравнения с образцом можно отнести структурные методы распознавания.
Статистические методы . Как видно из названия, статистические методы используют некоторую статистическую информацию при решении задачи распознавания. Метод определяет принадлежность объекта к конкретному классу на основе вероятности В ряде случаев это сводится к определению апостериорной вероятности принадлежности объекта к определенному классу, при условии, что признаки этого объекта приняли соответствующие значения. Примером служит метод на основе байесовского решающего правила.
Нейронные сети . Отдельный класс методов распознавания. Отличительной особенностью от других является способность обучаться.

Классификация по ближайшему среднему значению

В классическом подходе распознавания образов, в котором неизвестный объект для классификации представляется в виде вектора элементарных признаков. Система распознавания на основе признаков может быть разработана различными способами. Эти векторы могут быть известны системе заранее в результате обучения или предсказаны в режиме реального времени на основе каких-либо моделей.

Простой алгоритм классификации заключается в группировке эталонных данных класса с использованием вектора математического ожидания класса (среднего значения).

где x(i,j)- j-й эталонный признак класса i, n_j- количество эталонных векторов класса i.

Тогда неизвестный объект будет относиться к классу i, если он существенно ближе к вектору математического ожидания класса i, чем к векторам математических ожиданий других классов. Этот метод подходит для задач, в которых точки каждого класса располагаются компактно и далеко от точек других классов.

Трудности возникнут, если классы будут иметь несколько более сложную структуру, например, как на рисунке. В данном случае класс 2 разделен на два непересекающихся участка, которые плохо описываются одним средним значением. Также класс 3 слишком вытянут, образцы 3-го класса с большими значениями координат x_2 ближе к среднему значению 1-го класса, нежели 3-го.

Описанная проблема в некоторых случаях может быть решена изменением расчета расстояния.

Будем учитывать характеристику «разброса» значений класса - σ_i, вдоль каждого координатного направления i. Среднеквадратичное отклонение равно квадратному корню из дисперсии. Шкалированное евклидово расстояние между вектором x и вектором математического ожидания x_c равно

Эта формула расстояния уменьшит количество ошибок классификации, но на деле большинство задач не удается представить таким простым классом.

Классификация по расстоянию до ближайшего соседа

Другой подход при классификации заключается в отнесении неизвестного вектора признаков x к тому классу, к отдельному образцу которого этот вектор наиболее близок. Это правило называется правилом ближайшего соседа. Классификация по ближайшему соседу может быть более эффективна, даже если классы имеют сложную структуру или когда классы пересекаются.

При таком подходе не требуется предположений о моделях распределения векторов признаков в пространстве. Алгоритм использует только информацию об известных эталонных образцах. Метод решения основан на вычислении расстояния x до каждого образца в базе данных и нахождения минимального расстояния. Преимущества такого подхода очевидны:

в любой момент можно добавить новые образцы в базу данных;
древовидные и сеточные структуры данных позволяют сократить количество вычисляемых расстояний.

Кроме того, решение будет лучше, если искать в базе не одного ближайшего соседа, а k. Тогда при k > 1 обеспечивает наилучшую выборку распределения векторов в d-мерном пространстве. Однако эффективное использование значений k зависит от того, имеется ли достаточное количество в каждой области пространства. Если имеется больше двух классов то принять верное решение оказывается сложнее.

Литература

M. Castrillón, . O. Déniz, . D. Hernández и J. Lorenzo, «A comparison of face and facial feature detectors based on the Viola-Jones general object detection framework,» International Journal of Computer Vision, № 22, pp. 481-494, 2011.
Y.-Q. Wang, «An Analysis of Viola-Jones Face Detection Algorithm,» IPOL Journal, 2013.
Л. Шапиро и Д. Стокман, Компьютерное зрение, Бином. Лаборатория знаний, 2006.
З. Н. Г., Методы распознавания и их применение, Советское радио, 1972.
Дж. Ту, Р. Гонсалес, Математические принципы распознавания образов, Москва: “Мир” Москва, 1974.
Khan, H. Abdullah и M. Shamian Bin Zainal, «Efficient eyes and mouth detection algorithm using combination of viola jones and skin color pixel detection» International Journal of Engineering and Applied Sciences, № Vol. 3 № 4, 2013.
V. Gaede и O. Gunther, «Multidimensional Access Methods,» ACM Computing Surveys, pp. 170-231, 1998.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны - это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

где a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. - действительные константы, т.е.

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a o ,a n и b n называются коэффициентами Фурье , и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a 1 cosx+b 1 sinx) называется первой или основной гармоникой,

Другой способ записи ряда - использование соотношения acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Где a o - константа, с 1 =(a 1 2 +b 1 2) 1/2 , с n =(a n 2 +b n 2) 1/2 - амплитуды различных компонент, а равен a n =arctg a n /b n .

Для ряда (1) член (a 1 cosx+b 1 sinx) или c 1 sin(x+α 1) называется первой или основной гармоникой, (a 2 cos2x+b 2 sin2x) или c 2 sin(2x+α 2) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная , если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х 2 и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

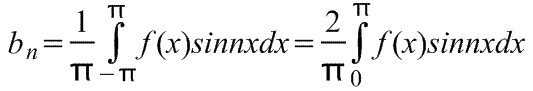
Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a o и a n

Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде .

Разложение по косинусам в диапазоне от 0 до L имеет вид

Ряд Фурье четной периодической функции f (x) с периодом 2р содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Разложение в ряд Фурье по синусам

Ряд Фурье нечетной периодической функции f (x) с периодом 2р содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье на полупериоде

Если функция определена для диапазона, скажем от 0 до р, а не только от 0 до 2р, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f (x) в диапазоне от 0 до р, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f (x) =х, построенная на интервале от х=0 до х=р. Поскольку четная функция симметрична относительно оси f (x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2р, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a o и a n

Если требуется получить разложение Фурье на полупериоде по синусам функции f (x) в диапазоне от 0 до р, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f (x) =x, построенная на интервале от от х=0 до х=р. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис.

Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2р, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b