Фигуры с центром симметрии примеры. Фигуры симметричные относительно точки (примеры). Как определяют симметрию разные словари

Государственное бюджетное профессиональное образовательное учреждение с.Тээли Республики Тыва

Разработка урока по математике

Тема урока:

«Однородные тригонометрические уравнения»

Преподаватель: Ооржак

Айлана Михайловна

Тема урока : «Однородные тригонометрические уравнения» (по учебнику А.Г. Мордковича)

Группа : Мастер растениеводства, 1 курс

Тип урока : Урок изучения нового материала.

Цели урока :

2. Развивать логическое мышление, умение делать выводы, умение оценивать результаты выполненных действий

3. Воспитывать у обучающихся аккуратность, чувство ответственности, воспитание положительных мотивов учения

Оборудование урока : ноутбук, проектор, экран, карточки, плакаты по тригонометрии: значения тригонометрических функций, основные формулы тригонометрии.

Продолжительность урока: 45 минут.

Структура урока:

Ход урока.

1. Организационный момент (1 мин)

Проверить готовность обучающихся к уроку, заслушать дежурных по группе.

2. Актуализация опорных знаний (3 мин)

2.1. Проверка домашнего задания.

Трое обучающихся решают у доски № 18.8 (в,г); № 18.19. Остальные обучающиеся делают взаимопроверку.

3. Изучение нового материала (13 мин)

3.1. Мотивация обучающихся.

Обучающимся предлагается назвать уравнения, которые они знают и могут решить (слайд № 1)

1) 3 cos 2 х – 3 cos х = 0;

2) cos (х – 1) = ;

3) 2 sin 2 х + 3 sin х = 0;

4) 6 sin 2 х – 5 cos х + 5 = 0; 1 2

5) sin х cos х + cos²х = 0;

6) tg + 3ctg = 4.

7) 2sin х – 3cos х = 0;

8) sin 2 х + cos 2 х = 0;

9) sin²х – 3sinх cos х+2cos²х = 0.

Обучающиеся не смогут назвать решение уравнений 7-9.

3.2. Объяснение новой темы.

Преподаватель: Уравнения, которые вы не смогли решить довольно часто встречаются на практике. Они называются однородными тригонометрическими уравнениями. Записать тему урока: «Однородные тригонометрические уравнения». (слайд № 2)

На экране проектора определение однородных уравнений. (слайд № 3)

Рассмотреть метод решения однородных тригонометрических уравнений (слайд № 4, 5)

Разобрать решение примеров

Пример 1. Решить уравнение 2sin х – 3cos х = 0; (слайд № 6)

Это однородное уравнение первой степени. Разделим обе части уравнения почленно на cos x , получим:

2tg x – 3 = 0

tg x =

x = arctg + πn , n Z.

Ответ: x = arctg + π n, n Z.

Пример 2 . Решить уравнение sin 2 х + cos 2 х = 0; (слайд № 7)

Это однородное уравнение первой степени. Разделим обе части уравнения почленно на cos 2 x , получим:

tg2 x + 1 = 0

tg2 x = - 1

2x = arctg (-1)+ πn, n Z.

2x = - + πn, n Z.

x = - + , n Z.

Ответ: x = - + , n Z.

Пример 3 . Решить уравнение sin²х – 3sinх cos х+2cos²х = 0. (слайд № 8)

Каждый член уравнения имеет одну и ту же степень. Это однородное уравнение второй степени. Разделим обе части уравнения почленно на сos 2 x ≠ 0, получим:

tg 2 x-3tg x+2 = 0. Введем новую переменную z = tg x, получим

z 2 – 3z + 2 =0

z 1 = 1, z 2 = 2

значит, либо tg x = 1, либо tg x = 2

4. Закрепление изученного материала (10 мин)

Преподаватель подробно разбирает примеры со слабыми обучающимися на доске, сильные обучающиеся самостоятельно решают в тетрадях.

5. Дифференцированная самостоятельная работа (15 мин)

Преподаватель выдает карточки с заданиями трех уровней: базовый (А), средний (В), повышенный (С). Обучающиеся сами выбирают, примеры какого уровня они будут решать.

6. Подведение итогов. Рефлексия учебной деятельности на уроке (2 мин)

Ответить на вопросы:

Какие виды тригонометрических уравнений мы изучили?

Как решается однородное уравнение первой степени?

Как решается однородное уравнение второй степени?

Я узнал …

Я научился …

Отметить хорошую работу на уроке отдельных обучающихся, выставить оценки.

7. Домашнее задание. (1 мин)

Сообщить обучающимся домашнее задание, дать краткий инструктаж по его выполнению.

№ 18.12 (в, г), № 18.24 (в,г), № 18.27 (а)

Использованная литература:

Слайд 2

«Однородные тригонометрические уравнения»

1. Уравнение вида а sin x + b cos x = 0, где а ≠0, b ≠0 называют однородным тригонометрическим уравнением первой степени. 2. Уравнение вида а sin 2 х + b sin х cos х + c cos 2 x = 0, где a ≠0, b ≠0, с ≠0 называют однородным тригонометрическим уравнением второй степени. Определение:

I степени a sinx + b cosx = 0, (a,b ≠ 0). Разделим обе части уравнения почленно на cosx ≠ 0. Получим: a tgx + b = 0 tgx = -b /а простейшее тригонометрическое уравнение При делении однородного уравнения a sinx + b cosx = 0 на cos x ≠ 0 корни этого уравнения не теряются. Метод решения однородных тригонометрических уравнений

a sin²x + b sinx cosx + c cos²x = 0. 1) если а ≠ 0, разделим обе части уравнения почленно на cos ² x ≠0 Получим: a tg ² x + b tgx + c = 0, решаем методом введения новой переменной z = tgx 2) если а = 0, то Получим: b sinx cosx + c cos ² x =0, решаем методом разложения на множители / При делении однородного уравнения a sin ² x + b sinx cosx + c cos ² x = 0 на cos 2 x ≠ 0 корни этого уравнения не теряются. II степени

Это однородное уравнение первой степени. Разделим обе части уравнения почленно на cos x , получим: Пример 1. Решить уравнение 2 sin х – 3 cos х = 0

Это однородное уравнение первой степени. Разделим обе части уравнения почленно на cos 2 x , получим: Пример 2 . Решить уравнение sin 2 х + cos 2 х = 0

Каждый член уравнения имеет одну и ту же степень. Это однородное уравнение второй степени. Разделим обе части уравнения почленно на с os 2 x ≠ 0, получим: Пример 3 . Решить уравнение sin ² х – 3 sin х cos х+2 cos ² х = 0

Ответьте на вопросы: - Какие виды тригонометрических уравнений мы изучили? -Как решается однородное уравнение первой степени? - Как решается однородное уравнение второй степени? Подведение итогов

Я узнал … - Я научился … Рефлексия

№ 18.12 (в, г), № 18.24 (в,г), № 18.27 (а) Домашнее задание.

Спасибо за урок! МОЛОДЦЫ!

Предварительный просмотр:

Самоанализ урока математики преподавателя Ооржак А.М.

Группа : Мастер растениеводства, 1 курс.

Тема урока : Однородные тригонометрические уравнения.

Тип урока : Урок изучения нового материала.

Цели урока:

1. Сформировать у обучающихся навыки решения однородных тригонометрических уравнений, рассмотреть методы решения однородных уравнений базового и повышенного уровня сложности.

2. Развивать логическое мышление, умение делать выводы, умение оценивать результаты выполненных действий.

3. Воспитывать у обучающихся аккуратность, чувство ответственности, воспитание положительных мотивов учения.

Урок проводился согласно тематического планирования. Тема урока отражает теоретическую и практическую часть урока и понятна обучающимся. Все этапы урока были направлены на выполнение этих целей с учетом особенностей группы.

Структура урока.

1.Организационный момент включал в себя предварительную организацию группы, мобилизующее начало урока, создание психологической комфортности и подготовку обучающихся к активному и сознательному усвоению нового материала. Подготовка группы и каждого обучающегося была проверена мною визуально. Дидактическая задача этапа: П оложительный настрой на урок.

2. Следующий этап – актуализация опорных знаний обучающихся. Основной задачей этого этапа является: восстановление в памяти обучающихся знаний, необходимых для изучения нового материала. Актуализация была проведена в форме проверки домашнего задания у доски.

3. (Основной этап урока) Формирование новых знаний. На этом этапе были реализованы следующие дидактические задачи: Обеспечение восприятия, осмысление и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения.

Этому способствовали: создание проблемной ситуации, метод бесед в сочетании с использованием ИКТ. Показателем эффективности усвоения обучающимися новых знаний является правильность ответов, самостоятельная работа, активное участие обучающихся в работе.

4.Следующий этап - первичное закрепление материала. Цель которого, установка обратной связи для получения информации о степени понимания нового материала, полноты, правильности его усвоения и для своевременной коррекции обнаруженных ошибок. Для этого я использовала: решение простых однородных тригонометрических уравнений. Здесь использовались задания из учебника, которые соответствуют обязательным результатам обучения. Первичное закрепление материала проводилось в атмосфере доброжелательности, сотрудничества. На этом этапе я работала со слабыми обучающимися, остальные решали самостоятельно, с последующей самопроверкой с доски.

5. Следующий момент урока был первичный контроль знаний. Дидактическая задача этапа: Выявление качества и уровня овладения знаниями и способами действий, обеспечение их коррекции. Здесь реализовала дифференцированный подход к обучению, предложила ребятам на выбор задания трех уровней: базовый (А), средний (В), повышенный (С). Сделала обход и отметила себе обучающихся, которые выбрали базовый уровень. Эти обучающиеся выполняли работу под контролем преподавателя.

6. На следующем этапе – подведение итогов, решались задачи анализа и оценки успешности достижения цели. Подводя итоги урока я одновременно осуществила рефлексию учебной деятельности. Обучающиеся усвоили способы решения однородных тригонометрических уравнений. Были выставлены оценки.

7. Заключительный этап – задание на дом. Дидактическая задача: Обеспечение понимания обучающихся содержания и способов выполнения домашнего задания. Дала краткий инструктаж по выполнению домашнего задания.

В ходе урока мне довелось реализовать обучающие, развивающие и воспитательные цели. Считаю, что этому способствовало то, что с первых минут урока ребята показали активность. Они были готовы к восприятию новой темы. Атмосфера в группе была психологически благоприятной.




С помощью этого видеоурока учащиеся смогут изучить тему однородных тригонометрических уравнений.

Дадим определения:

1) однородное тригонометрическое уравнение первой степени выглядит как a sin x + b cos x = 0;

2) однородное тригонометрическое уравнение второй степени выглядит как a sin 2 x + b sin x cos x + c cos 2 x = 0.

Рассмотрим уравнение a sin x + b cos x = 0. Если а будет равно нулю, то уравнение будет выглядеть как b cos x = 0; если b равно нулю, то уравнение будет выглядеть как a sin x = 0. Это уравнения, которые мы называли простейшими и решали ранее в предыдущих темах.

Сейчас рассмотрим вариант, когда a и b не равны нулю. С помощью деления частей уравнения на косинус x и осуществим преобразование. Получим a tg x + b = 0, тогда tg x будет равен - b/а.

Из вышеизложенного следует вывод, что уравнение a sin mx + b cos mx = 0 является однородным тригонометрическим уравнением I степени. Чтобы решить уравнение, его части делят на cos mx.

Разберем пример 1. Решить 7 sin (x/2) - 5 cos (x/2) = 0. Сначала части уравнения делим на косинус(x/2). Зная, что синус, деленный на косинус, это тангенс, получим 7 tg (x/2) - 5 = 0. Преобразовывая выражение, найдем, что значение тангенса (x/2)равно 5/7. Решение данного уравнения имеет вид х = arctg a + πn, в нашем случае х = 2 arctg (5/7) + 2πn.

Рассмотрим уравнение a sin 2 x + b sin x cos x + c cos 2 x = 0:

1) при а равном нулю уравнение будет выглядеть как b sin x cos x + c cos 2 x = 0. Преобразуя, получим выражение cos x (b sin x + c cos x) = 0 и перейдем к решению двух уравнений. После деления частей уравнения на косинус x, получим b tg x + c = 0, а значит tg x = - c/b. Зная, что х = arctg a + πn, то решением в данном случае будет х = arctg (- с/b) + πn.

2) если а не равно нулю, то, путем деления частей уравнения на косинус в квадрате, получим уравнение, содержащее тангенс, которое будет квадратным. Это уравнение можно решить путем ввода новой переменной.

3) при с равном нулю уравнение примет вид a sin 2 x + b sin x cos x = 0. Это уравнение можно решить, если вынести синус x за скобку.

1. посмотреть, есть ли в уравнении a sin 2 x;

2. если в уравнении член a sin 2 x содержится, то решить уравнение можно путем деления обеих частей на косинус в квадрате и последующим введением новой переменной.

3. если в уравнении a sin 2 x не содержится, то решить уравнение можно с помощью выноса за скобки cosx.

Рассмотрим пример 2. Вынесем за скобки косинус и получим два уравнения. Корень первого уравнения x = π/2 + πn. Для решения второго уравнения разделим части этого уравнения на косинус x, путем преобразований получим х = π/3 + πn. Ответ: x = π/2 + πn и х = π/3 + πn.

Решим пример 3, уравнение вида 3 sin 2 2x - 2 sin 2x cos 2x + 3 cos 2 2x = 2 и найдем его корни, которые принадлежат отрезку от - π до π. Т.к. это уравнение неоднородное, необходимо привести его к однородному виду. Используя формулу sin 2 x + cos 2 x = 1, получим уравнение sin 2 2x - 2 sin 2x cos 2x + cos 2 2x = 0. Разделив все части уравнения на cos 2 x, получим tg 2 2x + 2tg 2x + 1 = 0. Используя ввод новой переменной z = tg 2x, решим уравнение, корнем которого будет z = 1. Тогда tg 2x = 1, откуда следует, что x = π/8 + (πn)/2. Т.к. по условию задачи нужно найти корни, которые принадлежат отрезку от - π до π, решение будет иметь вид - π< x <π. Подставляя найденное значение x в данное выражение и преобразовывая его, получим - 2,25 < n < 1,75. Т.к. n - это целые числа, то решению уравнения удовлетворяют значения n: - 2; - 1; 0; 1. При этих значениях n получим корни решения исходного уравнения: x = (- 7π)/8, x = (- 3π)/8, x =π/8, x = 5π/8.

ТЕКСТОВАЯ РАСШИФРОВКА:

Однородные тригонометрические уравнения

Сегодня мы разберем, как решаются «Однородные тригонометрические уравнения». Это уравнения специального вида.

Познакомимся с определением.

Уравнение вида а sin x+ b cos x = 0 (а синус икс плюс бэ косинус икс равно нулю) называют однородным тригонометрическим уравнением первой степени;

уравнение вида а sin 2 x+ b sin x cos x +с cos 2 x = 0 (а синус квадрат икс плюс бэ синус икс косинус икс плюс сэ косинус квадрат икс равно нулю) называют однородным тригонометрическим уравнением второй степени.

Если а=0 , то уравнение примет вид b cos x = 0.

Еслиb = 0 , то получим а sin x= 0.

Данные уравнения являются элементарными тригонометрическими, и их решение мы рассматривали на прошлых наших темах

Рассмотрим тот случай, когда оба коэффициента не равны нулю. Разделим обе части уравнения а sin x + b cos x = 0 почленно на cos x .

Это мы можем сделать, так как косинус икс отличен от нуля. Ведь, если cos x = 0 , то уравнение а sin x + b cos x = 0 примет вид а sin x = 0 , а ≠ 0, следовательно sin x = 0 . Что невозможно, ведь по основному тригонометрическому тождеству sin 2 x+ cos 2 x =1 .

Разделив обе части уравнения а sin x + b cos x = 0 почленно на cos x , получим: + =0

Осуществим преобразования:

1. Так как = tg x, то = а tg x

2 сокращаем на cos x , тогда

Таким образом получим следующее выражение а tg x + b =0 .



Осуществим преобразование:

1.перенесем b в правую часть выражения с противоположным знаком

а tg x =- b

2. Избавимся от множителя а разделив обе части уравнения на а

tg x= - .

Вывод: Уравнение вида а sin m x+ b cos mx = 0 (а синус эм икс плюс бэ косинус эм икс равно нулю) тоже называют однородным тригонометрическим уравнением первой степени. Чтобы решить его, делят обе части на cos mx .

ПРИМЕР 1. Решить уравнение 7 sin - 5 cos = 0 (семь синус икс на два минус пять косинус икс на два равно нулю)

Решение. Разделим обе части уравнения почленно на cos, получим

1. = 7 tg (так как соотношение синуса к косинусу - это тангенс, то семь синус икс на два деленное на косинус икс на два, равно 7 тангенс икс на два)

2. -5 = -5 (при сокращении cos)

Таки образом получили уравнение

7tg - 5 = 0, Преобразуем выражение, перенесем минус пять в правую часть, изменив знак.

Мы привели уравнение к виду tg t = a, где t=, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg a + πn, то решение нашего уравнения будет иметь вид:

Arctg + πn, найдем х

х=2 arctg + 2πn.

Ответ: х=2 arctg + 2πn.

Перейдем к однородному тригонометрическому уравнению второй степени

а sin 2 x+b sin x cos x + с cos 2 x= 0.

Рассмотрим несколько случаев.

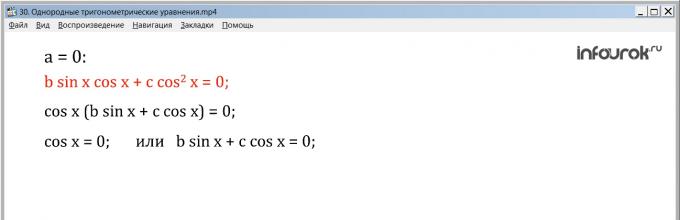
I. Если а=0 , то уравнение примет вид b sin x cos x +с cos 2 x = 0.

При решении э то уравнения используем метод разложения на множители. Вынесем cos x за скобку и получим: cos x (b sin x +с cos x )= 0 . Откуда cos x = 0 или

b sin x + с cos x= 0. А эти уравнения мы уже умеем решать.



Разделим обе части уравнения почленно на cosх, получим

1 (так как соотношение синуса к косинусу - это тангенс).

Таким образом получаем уравнение: b tg х+с=0

Мы привели уравнение к виду tg t = a, где t= х, a =. А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg a + πn, то решение нашего уравнения будет:

х = arctg + πn, .

II. Если а≠0 , то обе части уравнения почленно разделим на cos 2 x .

(Рассуждая аналогично, как и в случае с однородным тригонометрическим уравнением первой степени, косинус икс не может обратится в ноль).

III. Если с=0 , то уравнение примет вид а sin 2 x + b sin x cos x = 0. Это уравнение решается методом разложения на множители (вынесем sin x за скобку).

Значит, при решении уравнения а sin 2 x + b sin x cos x +с cos 2 x = 0 можно действовать по алгоритму:

ПРИМЕР 2. Решить уравнение sinxcosx - cos 2 x= 0 (синус икс, умноженный на косинус икс минус корень из трех, умноженный на косинус квадрат икс равно нулю).

Решение. Разложим на множители (вынесем за скобку cosx). Получим

cos x(sin x - cos x)= 0, т.е. cos x=0 илиsin x - cos x= 0.

Ответ: х =+ πn, х= + πn.

ПРИМЕР 3. Решить уравнение 3sin 2 2x - 2 sin2xcos2 x +3cos 2 2x= 2 (три синус квадрат двух икс минус удвоенное произведение синуса двух икс на косинус двух икс плюс три косинус квадрат двух икс) и найти его корни, принадлежащие промежутку (- π; π).

Решение. Это уравнение не однородное, поэтому проведем преобразования. Число 2, содержащееся в правой части уравнения, заменим произведением 2·1

Так как по основному тригонометрическому тождеству sin 2 x + cos 2 x =1, то

2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) = раскрыв скобки получим: 2 sin 2 x + 2 cos 2 x.

2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) =2 sin 2 x + 2 cos 2 x

Значит уравнение 3sin 2 2x - 2 sin2xcos2 x +3cos 2 2x= 2 примет вид:

3sin 2 2x - 2 sin 2x cos2 x +3cos 2 2x = 2 sin 2 x + 2 cos 2 x.

3sin 2 2x - 2 sin 2x cos2 x +3cos 2 2x - 2 sin 2 x - 2 cos 2 x=0,

sin 2 2x - 2 sin 2x cos2 x +cos 2 2x =0.

Получили однородное тригонометрическое уравнение второй степени. Применим способ почленного деления на cos 2 2x:

tg 2 2x - 2tg 2x + 1 = 0.

Введем новую переменную z= tg2х.

Имеем z 2 - 2 z + 1 = 0. Это квадратное уравнение. Заметив в левой части формулу сокращенного умножения - квадрат разности (), получим (z - 1) 2 = 0, т.е. z = 1. Вернемся к обратной замене:



Мы привели уравнение к виду tg t = a, где t= 2х, a =1 . А так как данное уравнение имеет решение для любого значения а и эти решения имеют вид

х = arctg x a + πn, то решение нашего уравнения будет:

2х= arctg1 + πn,

х= + , (икс равно сумме пи на восемь и пи эн на два).

Нам осталось найти такие значения х, которые содержатся в интервале

(- π; π), т.е. удовлетворяют двойному неравенству - π х π. Так как

х= + , то - π + π. Разделим все части этого неравенства на π и умножим на 8, получим

перенесем единицу в право и в лево, поменяв знак на минус один

разделим на четыре получим,

для удобства в дробях выделим целые части

-

Этому неравенству удовлетворяют следующие целочисленные n: -2, -1, 0, 1