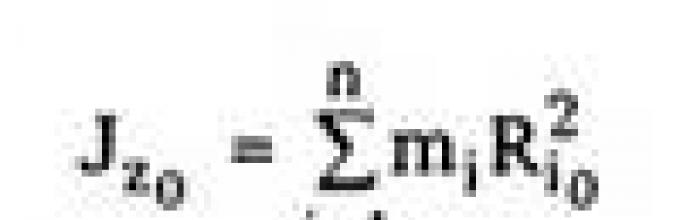т.е. момент инерции тела относительно
произвольной оси OZ равен моменту инерции
тела относительно оси OZq, проходящей через
центр масс тела параллельно оси OZ, плюс
произведение массы тела на квадрат расстояния
между осями OZ и OZq. Это утверждение иногда
называют теоремой о параллельных осях
или
теоремой Штейнера.
Именно поэтому, очень
важно знать (или уметь вычислять) моменты
инерции различных тел относительно осей OZq,
проходящих через центр масс тела.
Расчет момента инерции
![]()
производится на практике следующим образом:
если твердое тело сплошное, то его можно
разбить на бесконечно большое количество
бесконечно малых частей массы dm = pdV, где
р - плотность тела в данном месте, a dV - объем
кусочка dm, и суммирование заменить на
интегрирование по объему тела V, т.е.
где Rq - расстояние от кусочка dm до оси OZo.
В качестве примера вычислим момент инерции
тонкого однородного стержня (длиной L и массой
М) относительно перпендикулярной ему оси,
проходящей через его середину (центр масс

тонкого однородного стержня находится в его
середине). Направим ось ОХ вдоль стержня и
поместим начало координат в середине стержня
Укажем еще для примера, что момент инерции
полого цилиндра массой М и радиусом R
относительно оси цилиндра равен MR 2 . Если же
цилиндр сплошной, то его момент инерции

Рассмотренные выше простейшие виды
движения твердого тела - поступательное
движение и вращение - особенно важны потому,
что любое произвольное движение твердого тела
сводится к ним. Можно строго доказать, что
произвольное движение твердого тела можно
представить в виде совокупности поступательного
движения всего тела со скоростью какой -либо
его точки О и вращения вокруг оси, проходящей
через эту точку. При этом скорость
поступательного движения v 0 зависит от того,
какую именно точку мы выбрали.

сказать, что угловая скорость имеет "абсолютный"
характер, то есть можно говорить об угловой
скорости вращения твердого тела, не указывая
при этом, через какую именно точку проходит ось
вращения. Поступательная же скорость v 0 такого
"абсолютного" характера не имеет. Обычно в
качестве точки О выбирают центр масс тела.
Преимущества такого выбора выяснятся ниже.
5. Плоское движение
Рассмотрим наиболее простой вид
произвольного движения твердого тела, так
называемое плоское движение,
когда все точки
тела движутся в параллельных плоскостях,
ориентация которых в пространстве остается
неизменной, а тело вращается вокруг оси,
перпендикулярной этим плоскостям.
Будем рассматривать плоское движение в
неподвижной ИСО XYZ, причем плоскость XOY
совместим с плоскостью движения частиц, в
которой находится центр масс тела, скорость
которого v 0 = у цм относительно неподвижной
системы будем считать скоростью
поступательного движения тела (скорость v 0 ,
естественно, расположена в плоскости XOY).
Далее будем считать, что все силы f k ,
действующие на тело, параллельны плоскости
XOY. Тогда уравнение поступательного движения
тела можно записать в виде:
центра масс тела. Уравнение (3.12) проектируется
на оси ОХ и OY.
Уравнение вращательного движения тела
вокруг оси OZq,
проходящей через центр масс
тела перпендикулярно неподвижной плоскости
XOY, совпадает по форме с уравнением
вращательного движения тела вокруг
закрепленной оси (3.9):
Последнее утверждение (его можно строго
доказать!) выглядит довольно странным, так как
уравнение (3.9) было написано относительно ИСО,
система же отсчета (ось OZo), в которой
происходит вращение тела, не является
инерциальной, так как центр масс тела движется с
ускорением а 0 . Тем не менее это так, и связан
этот факт именно с тем, что мы выбрали в
качестве точки О при рассмотрении
поступательного движения центр масс тела. При
решении конкретных задач уравнения (3.12) и
(3.13) следует еще дополнить кинематическими
Существует ряд геометрических задач, которые околдовывают каждого, кто по воле случая сталкивается с ними. По-видимому, это было характерно для геометрии даже в древнее время. Стоит только вспомнить три знаменитые задачи древности — удвоение куба, трисекцию угла и квадратуру круга. Попытки решить эти задачи привели к развитию новых ветвей математики. Даже сейчас существуют псевдоматематики, которые присылают в редакции «решения» этих задач и требуют публикации или доказательства ложности своих «решений».
Одна всегда возбуждавшая интерес теорема может быть сформулирована следующим образом:
Если в треугольнике две биссектрисы равны, то этот треугольник является равнобедренным.
Это с виду простое утверждение не имеет простого классического доказательства. Этот факт тем более удивителен, что заменив слово "биссектрисы" на "медианы" или "высоты", получаем утверждения, доказательства которых элементарны.
Эта теорема была послана великому шведскому геометру, члену Берлинской академии наук, Якобу Штейнеру в 1840 году Кристианом Лудольфом Лемусом, немецким математиком, профессором Берлинского университете, с просьбой дать чисто геометрическое доказательство.

Якоб Штейнер
(1796-1863 )
Штейнер дал довольно сложное доказательство, которое вдохновило многих других на поиски более простых методов. Работы по теореме Штейнера - Лемуса появлялись в различных журналах в 1842, 1844, 1848 годах и почти каждый год с 1854 года по 1864 год, а также в большом количестве и в течение следующего столетия.
Доказательство теоремы Штейнера - Лемуса
Одно из простейших доказательств опирается на следующие две леммы:
Лемма 1.
Если две хорды окружности стягивают различные острые углы с вершинами на этой окружности, то меньшему углу соответствует меньшая хорда.
Доказательство.
Две равные хорды стягивают равные углы с вершиной в центре окружности и равные углы (как их половины) с вершинами в соответствующих точках на окружности. Из двух неравных хорд более короткая, находясь дальше от центра, стягивает меньший угол с вершиной в центре и, следовательно, меньший острый угол с вершиной на окружности.
Лемма 2.
В треугольнике с двумя различными углами меньший угол обладает большей биссектрисой .
Доказательство.

Пусть ABC — треугольник, в котором угол B меньше угла C , как на рисунке выше; пусть отрезки BM и CN делят пополам углы B и C . Мы хотим доказать, что BM < CN . Возьмем точку M′ на отрезке BM так, чтобы
∠M′CN = 1 / 2 ∠B .
Так как этот угол равен углу M′BN , то четыре точки N, B, C, М′ лежат на одной окружности. Поскольку
∠B < 1 / 2 (∠B + ∠C) < 1 / 2 (∠A + ∠B + ∠C) ,
то
∠CBN < ∠M′CB < 90° .
По лемме 1: CN < M′B . Следовательно, BM > BM′ > CN .
Вернёмся теперь непосредственно к доказательству теоремы Штейнера - Лемуса. Часто случается, что теорема может быть выражена в форме "противоположной к обратной" - эквивалентной первоначальной. Например, вместо того, чтобы сказать: " Все люди смертны" , мы можем также сказать " Бессмертные не есть люди" . Вместо доказательства самой теоремы Штейнера - Лемуса для нас будет достаточно доказать, что
если в треугольнике ABC ∠B ≠ ∠C , то BM ≠ CN .
Но это есть прямое следствие леммы 2.
Лирико-математическое отступление
Вышеприведенное доказательство этой леммы имеет занятную историю. Оно было придумано двумя английскими инженерами Г. Джильбертом и Д. Мак-Доннеллом и опубликовано в 1963 году в журнале American Mathematical Monthly со следующим редакционным примечанием:
Мартин Гарднер в своем обзоре книги Коксетера "Введение в геометрию" описал эту знаменитую теорему столь интересно, что сотни читателей прислали ему свои доказательства. Он взял на себя труд по обработке этого громадного материала и совершенствовал его до тех пор, пока не заблистала, очищенная от наслоений, жемчужина, которую мы приводим здесь.
Некоторые читатели могут испытать чувство неудовлетворенности потому, что "воздушное" доказательство Джильберта и Мак-Доннелла является косвенным: вместо самой теоремы Штейнера - Лемуса они доказывают теорему, противоположную к обратной (лемма 2).
Было предложено несколько якобы прямых доказательств; но каждое из них в действительности является в скрытой форме косвенным. Это несложно понять, если вспомнить, что практически только самые элементарные теоремы доказываются полностью. Все остальные доказываются с помощью других, уже известных теорем, которые выстраиваются в ряд, ведущий к аксиомам. Нельзя, строго говоря, утверждать, что некое доказательство - прямое, если хоть одна из этих вспомогательных теорем имеет косвенное доказательство. Более того, некоторые из самых простых и самых основных теорем имеют косвенные доказательства; следовательно, если бы мы настаивали на абсолютно прямом доказательстве, то существующее великое множество теорем свелось бы к небольшому числу тривиальных.
Стоит ли об этом сожалеть? Великий английский математик Годфри Харольд Харди (1877-1947) говорил по этому поводу:
Reductio ad absurdum (лат. приведение к абсурду), столь любимое Евклидом , является тончайшим инструментом математика. Оно является намного более тонким гамбитом, чем любой шахматный гамбит: шахматист может предложить в жертву пешку или другую фигуру, а математик предлагает в жертву всю игру.
Алгебраическое доказательство теоремы Штейнера - Лемуса
Приведем полное прямое, хотя и несколько тяжеловесное, доказательство теоремы Штейнера - Лемуса. Для этого воспользуемся следующей теоремой:

Пусть Х - точка на стороне АС треугольника АВС, причём АВ = с , ВС = а , АС = b , ВХ = р , АХ = m , XC = n . Тогда
b (p 2 + mn) = a 2 m + c 2 n .
Этот результат называется теоремой Стюарта в честь английского математика М. Стюарта, который сформулировал её в труде «Некоторые общие теоремы» (1746, Эдинбург). Теорему сообщил Стюарту его учитель Роберт Симсон (1687-1768) который опубликовал и доказал эту теорему лишь в 1749 году (по другим сведениям, - в 1751 году).
Доказательство.
По теореме косинусов из треугольников АВХ и ВСХ имеем:
c 2 = р 2 + m 2 - 2рm · cos α ,
а 2 = р 2 + n 2 - 2рn · cos (π - α ) = р 2 + n 2 + 2рn · cos α .
Тогда
c 2 n = р 2 n + m 2 n - 2рmn · cos α ,
а 2 m = р 2 m + n 2 m + 2рmn · cos α
c 2 n + а 2 m = р 2 (m + n) + mn (m + n) ,
c 2 n + а 2 m = (m + n) (р 2 + mn) ,
c 2 n + а 2 m = b (р 2 + mn) ,
что и требовалось доказать.
Продолжим рассуждения. Если р - биссектриса, то легко получить, что
| m = | bc | и n = | ab | . |
| a + c | a + c |
Тогда по теореме Стюарта
| c 2 · ab | + | а 2 · bc |
= b (р 2 + | ab 2 c | ) , |
| a + c | a + c | (a + c) 2 |
| ac 2 + а 2 c | = р 2 + | ab 2 c | , |
| a + c | (a + c) 2 |
| ac (c + a ) | = р 2 + | ab 2 c | , |
| a + c | (a + c) 2 |
| р 2 = ac (1 - | b 2 | ) . (*) |
| (a + c) 2 |
Приступим к непосредственному доказательству теоремы Штейнера - Лемуса.

Пусть k и l - равные биссектрисы треугольника АВС , проведённые к сторонам АВ = с и ВС = а . Тогда
k 2 = l 2
и, согласно полученному выше равенству (*), имеем:
| bc (1 - | a 2 | ) = ab (1 - | c 2 | ) , |
| (b + c ) 2 | (a + b ) 2 |
| c ( 1 - | a | ) (1 + | a | ) = a (1 - | c | ) (1 + | c | ) , |
| b + c | b + c | a + b | a + b |
| c (b + c - a ) (a +b + c ) | = | a (a + b - c ) (a +b + c ) | , |
| (b + c ) 2 | (a + b ) 2 |
| c (b + c - a ) | = | a (a + b - c ) | , |
| (b + c ) 2 | (a + b ) 2 |
a ((a - c ) + b ) (b + c ) 2 + c ((a - c ) - b ) (a + b ) 2 = 0 ,
a (a - c ) (b + c ) 2 + ab (b + c ) 2 + c (a - c ) (a + b ) 2 - bc (a + b ) 2 = 0 ,
(a - c ) (a (b + c ) 2 + c (a + b ) 2 ) + (ab (b + c ) 2 - bc (a + b ) 2 ) = 0 ,
(a - c ) (b 2 (a + c ) + ac (a + c ) + 4abc ) + b 3 (a - c ) - abc (a - c ) = 0 ,
(a - c ) ((a + c ) (b 2 + ab ) + 3abc + b 3 ) = 0 ,
откуда
a - c = 0
и, следовательно,
а = с ,
что и требовалось доказать.
P. S.
1. Ещё с одним прямым доказательством теоремы Штейнера - Лемуса можно познакомиться на сайте Математика, которая мне нравится .
2. В советской и российской литературе распространено доказательство, основанное на следующем признаке равенства треугольников:
если сторона, противолежащий этой стороне угол и биссектриса этого угла одного треугольника равны соответствующим элементам другого треугольника, то такие треугольники равны .
Использованные источники: Г.С.М. Коксетер, С.Л. Грейтцер "Новые встречи с геометрией" (Москва, "Наука" ГРФМЛ, 1978) и Википедия.
Уважаемые посетители сайта , предлагает Вашему вниманию работу по математике на тему , где представлены материалы теоретического и практического характера, рекомендации по решению задач с использованием указанной теоремы.
Теорема Штейнера , или, как именуется она в других источниках, теорема Гюйгенса-Штейнера, получила свое название в честь ее автора – Якоба Штейнера (швейцарского математика), а также благодаря дополнениям – Христиана Гюйгенса (голландского физика, астронома и математика). Рассмотрим кратко их вклад в и других наук.
Теорема Штейнера — об авторах теоремы

Якоб Штейнер
(1796—1863)
Якоб Штейнер (1796—1863) — один из , который считается основателем, как синтетической геометрии кривых линий, так и поверхностей второго и высших порядков.
Что касается Христиана Гюйгенса, то его вклад в различные науки тоже не мал. Он значительно усовершенствовал (до 92-кратного увеличения изображения), открыл кольца Сатурна и спутник его — Титан, а в 1673 году в своем довольно содержательном труде «Маятниковые часы», представил работы по кинематике ускоренного .
Теорема Штейнера — формулировка
Согласно теореме Штейнера, установлено, что момент инерции тела при расчете относительно произвольно оси соответствует сумме момента инерции тела относительно такой оси, которая проходит через центр масс и является параллельной данной оси, а также плюс произведение квадрата расстояния между осями и массы тела, по следующей формуле (1):
J= J 0 + md 2 (1)
Где в формуле принимаем соответственно величины: d
– расстояние между осями ОО 1 ║О’O 1 ’;
J 0
– момент инерции тела, рассчитанный относительно оси, что проходит сквозь центр масс и будет определяться соотношением (2):
J 0 = J d = mR 2 /2 (2)

Так как d = R, тогда и момент инерции относительно оси, которая проходит через указанную на рисунке точку А будет определяется формулой (3):
J = mR 2 + mR 2 /2 = 3 / 2 mR 2 (3)
Более подробная информация о теореме представлена в реферате и презентации, которые можно скачать по ссылкам перед статьей.
Теорема Штейнера. Момент инерции – содержание работы
Введение
Часть 1. Динамика вращения твердого тела
1.1. Моменты инерции шара и диска
1.2. Теорема Гюйгенса-Штейнера
1.3. Динамика вращательного движения твердого тела — теоретические основы
Момент импульса
Момент силы
Момент инерции относительно оси вращения
Главный закон динамики вращательного движения твердого тела относительно неподвижной оси
Момент инерции определяется как , если распределение массы равномерно, то заменяется на – элементарный объём, – плотность вещества. .
Теорема Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тала на квадрат расстояния а между осями: .
Момент инерции:
1) однородного тонкого стержня массы , длины относительно оси, проходящей через центр масс и перпендикулярной стержню:
2) однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня:
3) тонкого кольца массы , радиуса R относительно оси симметрии, перпендикулярной плоскости кольца:
4) однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию: .
21. Кинетическая энергия вращающегося твёрдого тела.
При вращении тела с угловой скоростью все его элементарные массы движутся со скоростью они обладают кинетической энергией , – для тела, вращающегося вокруг неподвижной оси. При вращении на материальные точки массы , образующие твёрдое тело, действуют как внешние, так и внутренние силы. За промежуток времени испытывает перемещение ,при этом силы совершают работу . Работа всех сил будет равна . При сложении с учётом 3-его закона Ньютона сумма работ внутренних сил = 0. Следовательно, . В соответствии с теоремой о кинетической энергии, приращение кинетической энергии = работе всех сил, действующих на тело .
Вычислим кинетическую энергию твёрдого тела, совершающего произвольное плоское движение. все точки движутся в параллельных плоскостях. Вращение совершается вокруг оси, перпендикулярно плоскостям, и движется вместе с некоторой точкой О. Скорость материальной точки массы представим в виде . Тело перемещается поступательно, следовательно, , – выражение кинетической энергии тела, совершающего произвольное плоское движение. Если в качестве точки О выбрать центр масс, тогда и .
Гироскопы.
Гироскоп (или волчок) – массивное твёрдое тело, симметричное некоторой оси, совершающее вращения вокруг неё с большой угловой скоростью. В силу симметрии гироскопа выполняется . При попытке повернуть вращающийся гироскоп вокруг некоторой оси наблюдается гироскопический эффект – под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой О’O’, ось гироскопа поворачивается вокруг прямой О’’О’’ (ось ОО и прямая О’O’ предполагаются лежащими в плоскости чертежа, а прямая О’’О’’ и силы f1 и f2 – перпендикулярными к этой плоскости). Объяснение эффекта основано на использование уравнения момента . Момент импульса поворачивается вокруг оси ОХ в силу соотношения . Вместе с вокруг ОХ поворачивается и гироскоп. Вследствие гироскопического эффекта на подшипнике, на котором вращается гироскоп, начинают действовать гироскопические силы . Под действием гироскопических сил ось гироскопа стремиться занять положение, параллельное угловой скорости вращения Земли.
Описанное поведение гироскопа положено в основу гироскопического компаса . Преимущества гироскопа: указывает точное направление на географический северный полюс, его работа не подвержена воздействию металлических предметов.
Прецессия гироскопа
– особый вид движения гироскопа имеет место в том случае, если момент действующих на гироскоп внешних сил, оставаясь постоянным по величине, поворачивается одновременно с осью гироскопа, образуя с ней всё время прямой угол. Рассмотрим движение гироскопа с одной закреплённой точкой на оси под действием силы тяжести , – расстояние от закреплённой точки до центра инерции гироскопа, – угол между гироскопом и вертикалью. направлен момент перпендикулярно к вертикальной плоскости, проходящей через ось гироскопа. Уравнение движения: приращение импульса = Следовательно, изменяет своё положение в пространстве таким образом, что его конец описывает окружность в горизонтальной плоскости. За промежуток времени гироскоп повернулся на угол ![]() ось гироскопа описывает конус вокруг вертикальной оси с угловой скоростью – угловая скорость прецессии.
ось гироскопа описывает конус вокруг вертикальной оси с угловой скоростью – угловая скорость прецессии.
Предположим, что мы умеем вычислять моменты инерции относительно любой оси, проходящей через центр масс. Теперь возникает задача вычисления момента инерции тела относительно произвольной оси. Она решается с помощью теоремы Штейнера.
Эта теорема утверждает, что момент инерции тела относительно любой оси вращения равен моменту инерции относительно параллельной ей оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.
Для доказательства теоремы рассмотрим некую ось С , проходящую через центр масс и параллельную ей ось О , отстоящую от оси С на расстоянии а. Ось О может находиться и вне тела. Обе оси перпендикулярны плоскости чертежа (рис. 2.12).
Рис. 2.12. К доказательству теоремы Штейнера
Из рис. 2.12 видно, что положение элемента массы относительно этих осей определяется векторами и , связь между которыми имеет вид:
Квадрат расстояния равен скалярному произведению
Тогда момент инерции тела относительно оси О можно представить в следующем виде:
Последнее слагаемое в этом выражении есть момент инерции тела относительно оси, проходящей через центр масс. Обозначим его через Сумма ![]() . Напомним, что оси О
и С
параллельны и следовательно, вектор перпендикулярен оси С.
Поэтому скалярное произведение Таким образом, мы получаем:
. Напомним, что оси О
и С
параллельны и следовательно, вектор перпендикулярен оси С.
Поэтому скалярное произведение Таким образом, мы получаем:
![]() (2.10.1)
(2.10.1)
Уравнение движения твердого тела.
Абсолютно твердое тело имеет шесть степеней свободы и, следовательно, его движение описывается с помощью шести дифференциальных уравнений второго порядка. Три из них описывают движение центра масс твердого тела:
 ,
,  ,
,  , (2.11.1)
, (2.11.1)
где — координаты центра масс тела, — проекции внешних сил на оси координат, m — масса тела. Три других являются уравнениями моментов относительно осей ОХ , ОУ и ОZ в декартовой системе координат:
 ,
,  ,
,  , (2.11.2)
, (2.11.2)
где L x , L y , L z — моменты импульса системы относительно осей ОХ , ОУ , ОZ , а M x , M y , M z — моменты внешних сил относительно этих же осей.
Если перемещать точку приложения силы вдоль линии ее действия, то моменты сил и результирующие силы не будут меняться, если мы имеем дело с абсолютно твердым телом. В этом случае не будут меняться и уравнения движения (2.11.1), (2.11.2).
Если найдены решения уравнений (2.11.1), (2.11.2), при известных начальных условиях, то определены и шесть координат, характеризующих движение твердого тела. Эти координаты являются функциями времени. Однако системы уравнений (2.11.1) и (2.11.2) не всегда позволяют получить решение в аналитической форме. В этом случае говорят, что уравнение движения не удается проинтегрировать, и решение уравнений находят путем численного интегрирования.