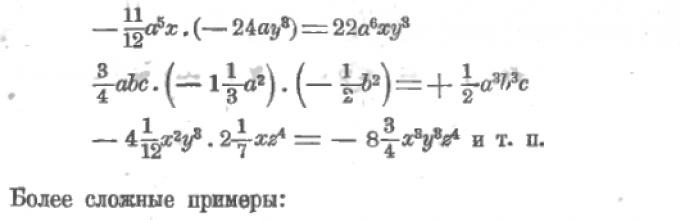Округление чисел - простейшая математическая операция. Чтобы уметь правильно округлять числа, необходимо знать три правила.
Правило 1
Когда мы округляем число до какого-то разряда, мы должны избавиться от всех цифр справа от этого разряда.
Например, нам нужно округлить число 7531 до сотен. В этом числе пять сотен. Справа от этого разряда стоят цифры 3 и 1. Превращаем их в нули и получаем число 7500. То есть, округлив число 7531 до сотен, мы получили 7500.
При округлении дробных чисел все происходит так же, только лишние разряды можно просто отбросить. Допустим, нам нужно округлить число 12,325 до десятых. Для этого после запятой мы должны оставить одну цифру - 3, а все цифры, стоящие справа, отбрасываем. Результат округления числа 12,325 до десятых - 12,3.
Правило 2
Если справа от оставляемой цифры отбрасываемая цифра равна 0, 1, 2, 3 или 4, то цифра, которую мы оставляем, не меняется.
Это правило сработало в двух предыдущих примерах.
Так, при округлении числа 7531 до сотен самой близкой к оставляемой цифре из отбрасываемых была тройка. Поэтому цифра, которую мы оставили, - 5 - не изменилась. Результатом округления стало число 7500.
Точно так же при округлении числа 12,325 до десятых цифрой, которую мы отбросили после тройки, была двойка. Поэтому самая правая из оставленных цифр (тройка) при округлении не изменилась. Получилось 12,3.
Правило 3
Если же самая левая из отбрасываемых цифр равна 5, 6, 7, 8 или 9, то разряд, до которого мы округляем, увеличивается на единицу.
Например, нужно округлить число 156 до десятков. В этом числе 5 десятков. В разряде единиц, от которого мы собираемся избавиться, стоит цифра 6. Значит, разряд десятков нам следует увеличить на единицу. Поэтому при округлении числа 156 до десятков мы получим 160.
Рассмотрим пример с дробным числом. Например, мы собираемся округлить 0,238 до сотых. По правилу 1 мы должны отбросить восьмёрку, которая стоит справа от разряда сотых. А по правилу 3 нам придётся увеличить тройку в разряде сотых на один. В итоге, округлив число 0,238 до сотых, мы получим 0,24.
Округление мы часто используем в повседневной жизни. Если расстояние от дома до школы будет 503 метра. Мы можем сказать, округлив значение, что расстояние от дома до школы 500 метров. То есть мы приблизили число 503 к более легко воспринимающемуся числу 500. Например, булка хлеба весит 498 грамм, то можно сказать округлив результат, что булка хлеба весит 500 грамм.
Округление – это приближение числа к более “легкому” числу для восприятия человека.
В итоге округления получается приближенное число. Округление обозначается символом ≈, такой символ читается “приближённо равно”.
Можно записать 503≈500 или 498≈500.
Читается такая запись, как “пятьсот три приближенно равно пятистам” или “четыреста девяносто восемь приближенно равно пятистам”.
Разберем еще пример:
44 71≈4000 45 71≈5000
43 71≈4000 46 71≈5000
42 71≈4000 47 71≈5000
41 71≈4000 48 71≈5000
40 71≈4000 49 71≈5000
В данном примере было произведено округление чисел до разряда тысяч. Если посмотреть закономерность округления, то увидим, что в одном случае числа округляются в меньшую сторону, а в другом – в большую. После округления все остальные числа после разряда тысяч заменили на нули.
Правила округления чисел:
1) Если округляемая цифра равна 0, 1, 2, 3, 4, то цифра разряда до которого идет округление не меняется, а остальные числа заменяются нулями.
2) Если округляемая цифра равна 5, 6, 7, 8, 9, то цифра разряда до которого идет округление становиться на 1 больше, а остальные числа заменяются нулями.
Например:
1) Выполните округление до разряда десятков числа 364.
Разряд десятков в данном примере это число 6. После шестерки стоит число 4. По правилу округления цифра 4 разряд десятков не меняет. Записываем вместо 4 нуль. Получаем:
36 4 ≈360
2) Выполните округление до разряда сотен числа 4 781.
Разряд сотен в данном примере это число 7. После семерки стоит цифра 8, которая влияет на то измениться ли разряд сотен или нет. По правилу округления цифра 8 увеличивает разряд сотен на 1, а остальные цифры заменяем нулями. Получаем:
47 8 1≈48 00
3) Выполните округление до разряда тысяч числа 215 936.
Разряд тысяч в данном примере это число 5. После пятерки стоит цифра 9, которая влияет на то измениться ли разряд тысяч или нет. По правилу округления цифра 9 увеличивает разряд тысяч на 1, а остальные цифры заменяются нулями. Получаем:
215 9 36≈216 000
4) Выполните округление до разряда десятков тысяч числа 1 302 894.
Разряд тысяч в данном примере это число 0. После нуля стоит цифра 2, которая влияет на то измениться ли разряд десятков тысяч или нет. По правилу округления цифра 2 разряд десятков тысяч не меняет, заменяем на нуль этот разряд и все разряды младшие разряды. Получаем:
130 2 894≈130 0000
Если точное значение числа неважно, то значение числа округляют и можно выполнять вычислительные операции с приближенными значениями . Результат вычисления называют прикидкой результата действий .
Например: 598⋅23≈600⋅20≈12000 сравним с 598⋅23=13754
Прикидкой результата действий пользуются для того, чтобы быстро посчитать ответ.
Примеры на задания по теме округление:
Пример №1:
Определите до какого разряда сделано округление:
а) 3457987≈3500000 б)4573426≈4573000 в)16784≈17000
Вспомним какие бывают разряды на числе 3457987.
7 – разряд единиц,
8 – разряд десятков,
9 – разряд сотен,
7 – разряд тысяч,
5 – разряд десятков тысяч,
4
– разряд сотен тысяч,
3 – разряд миллионов.
Ответ: а) 3 4
57 987≈3 5
00 000 разряд сотен тысяч б) 4 573
426≈4 573
000 разряд тысяч в)16
7 841≈17
0 000 разряд десятков тысяч.
Пример №2:
Округлите число до разрядов 5 999 994: а) десятков б) сотен в) миллионов.
Ответ: а) 5 999 994
≈5 999 990 б) 5 999 99
4≈6 000 000 (т.к. разряды сотен, тысяч, десятков тысяч, сотен тысяч цифра 9, каждый разряд увеличился на 1) 5 9
99 994≈6 000 000.
§ 1 Умножение многочлена на одночлен
Когда речь идёт об умножении многочленов, то мы можем иметь дело с операциями двух видов: умножение многочлена на одночлен и умножение многочлена на многочлен. На этом занятии мы узнаем, как умножить многочлен на одночлен.
Основным правилом, которое используют при умножении многочлена на одночлен, является распределительное свойство умножения. Вспомним:
Чтобы сумму умножить на число, можно каждое слагаемое умножить на это число и полученные произведения сложить.
Это свойство умножения распространяется и на действие вычитания. В буквенной записи распределительное свойство умножения выглядит так:
(а + b) ∙ с = ас + bc
(а - b) ∙ с = ас - bc
Рассмотрим пример: многочлен (5аb - 3а2) умножить на одночлен 2b.
Введём новые переменные и обозначим 5аb - буквой х, 3а2 - буквой у, 2b - буквой с. Тогда наш пример примет вид:
(5аb - 3а2) ∙ 2b = (х - у) ∙с
Согласно распределительному закону это равно хс - ус. Теперь вернёмся к первоначальному значению новых переменных. Получим:
5аb∙2b - 3а2∙2b
Теперь приведём получившийся многочлен к стандартному виду. Получим выражение:
Таким образом, можно сформулировать правило:
Чтобы умножить многочлен на одночлен, надо каждый член многочлена умножить на этот одночлен и полученные произведения сложить.
Это же правило действует и при умножении одночлена на многочлен.
§ 2 Примеры по теме урока
При умножении многочленов на практике во избежание путаницы с определением получающихся знаков рекомендуют сначала определять и сразу записывать знак произведения, а уж потом находить и записывать произведение чисел и переменных. Вот как это выглядит на конкретных примерах.
Пример 1. (4а2b - 2а) ∙ (-5аb).
Здесь одночлен - 5аb надо умножить на два одночлена, составляющих многочлен, 4а2b и - 2а. Первое произведение будет со знаком «-», а второе - со знаком «+». Поэтому решение будет выглядеть так:
(4а2b - 2а) ∙ (-5аb) = - 4а2b ∙ 5аb + 2а ∙ 5аb = -20а3b2 + 10а2b
Пример 2. -ху(2х - 3у +5).
Здесь нам придётся выполнить три действия умножения, причём знак первого произведения будет «-», знак второго «+», знак третьего «-». Решение выглядит так:
Ху(2х - 3у + 5) = -ху∙2х + ху∙3у - ху∙5 = -2х2у + 3ху2 - 5ху.
Список использованной литературы:
- Мордкович А.Г, Алгебра 7 класс в 2 частях, Часть 1, Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 10 – е изд., переработанное – Москва, «Мнемозина», 2007
- Мордкович А.Г., Алгебра 7 класс в 2 частях, Часть 2, Задачник для общеобразовательных учреждений/ [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича – 10-е издание, переработанное – Москва, «Мнемозина», 2007
- Е.Е. Тульчинская, Алгебра 7 класс. Блиц опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008
- Александрова Л.А., Алгебра 7 класс. Тематические проверочные работы в новой форме для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений, под редакцией А.Г. Мордковича – 6-е издание, стереотипное, Москва, «Мнемозина», 2010
Если числа обозначены различными буквами, то можно лишь обозначить из произведение; пусть, напр., надо число a умножить на число b, – мы можем это обозначить или a ∙ b или ab, но не может быть и речи о том, чтобы как-нибудь выполнить это умножение. Однако, когда имеем дело с одночленами, то, благодаря 1) присутствию коэффициентов и 2) тому обстоятельству, что в состав этих одночленов могут входить множители, обозначенные одинаковыми буквами, является возможность говорить о выполнении умножения одночленов; еще шире такая возможность при многочленах. Разберем ряд случаев, где возможно выполнять умножение, начиная с простейшего.
1. Умножение степеней с одинаковыми основаниями . Пусть, напр., требуется a 3 ∙ a 5 . Напишем, зная смысл возведения в степень, то же самое подробнее:
a ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a
Рассматривая эту подробную запись, мы видим, что у нас написано a множителем 8 раз, или, короче, a 8 . Итак, a 3 ∙ a 5 = a 8 .
Пусть требуется b 42 ∙ b 28 . Пришлось бы написать сначала множитель b 42 раза, а затем опять множитель b 28 раз – в общем, получили бы, что b берется множителем 70 раз. т. е. b 70 . Итак, b 42 ∙ b 28 = b 70 . Отсюда уже ясно, что при умножении степеней с одинаковыми основаниями основание степени остается без перемены, а показатели степеней складываются. Если имеем a 8 ∙ a, то придется иметь в виду, что у множителя a подразумевается показатель степени 1 («a в первой степени»), – следовательно, a 8 ∙ a = a 9 .
Примеры: x ∙ x 3 ∙ x 5 = x 9 ; a 11 ∙ a 22 ∙ a 33 = a 66 ; 3 5 ∙ 3 6 ∙ 3 = 3 12 ; (a + b) 3 ∙ (a + b) 4 = (a + b) 7 ; (3x – 1) 4 ∙ (3x – 1) = (3x – 1) 5 и т. д.
Иногда приходится иметь дело со степенями, показатели которых обозначены буквами, напр., xn (x в степени n). С такими выражениями надо привыкнуть обращаться. Вот примеры:
Поясним некоторые из этих примеров: b n – 3 ∙ b 5 надо основание b оставить без перемены, а показатели сложить, т. е. (n – 3) + (+5) = n – 3 + 5 = n + 2. Конечно, подобные сложения должно научиться выполнять быстро в уме.
Еще пример: x n + 2 ∙ x n – 2 , – основание x надо оставить без перемены, а показатель сложить, т. е. (n + 2) + (n – 2) = n + 2 + n – 2 = 2n.
Можно выше найденный порядок, как выполнять умножение степеней с одинаковыми основаниями, выразить теперь равенством:
a m ∙ a n = a m + n
2. Умножение одночлена на одночлен. Пусть, напр., требуется 3a²b³c ∙ 4ab²d². Мы видим, что здесь обозначено точкою одно умножение, но мы знаем, что этот же знак умножения подразумевается между 3 и a², между a² и b³, между b³ и c, между 4 и a, между a и b², между b² и d². Поэтому мы можем здесь видеть произведение 8 множителей и можем перемножить их любыми группами в любом порядке. Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями оказались рядом, т. е.
3 ∙ 4 ∙ a² ∙ a ∙ b³ ∙ b² ∙ c ∙ d².
Тогда мы сможем перемножить 1) коэффициенты и 2) степени с одинаковыми основаниями и получим 12a³b5cd².
Итак, при умножении одночлена на одночлен мы можем перемножить коэффициенты и степени с одинаковыми основаниями, а остальные множители приходится переписывать без изменения.
Еще примеры:

3. Умножение многочлена на одночлен. Пусть надо сначала какой-нибудь многочлен, напр., a – b – c + d умножить на положительное целое число, напр., +3. Так как положительные числа считаются совпадающими с арифметическими, то это все равно, что (a – b – c + d) ∙ 3, т. е. a – b – c + d взять 3 раза слагаемым, или
(a – b – c + d) ∙ (+3) = a – b – c + d + a – b – c + d + a – b – c + d = 3a – 3b – 3c + 3d,
т. е. в результате пришлось каждый член многочлена умножить на 3 (или на +3).
Отсюда вытекает:
(a – b – c + d) ÷ (+3) = a – b – c + d,
т. е. пришлось каждый член многочлена разделить на (+3). Также, обобщая, получим:
![]() и т. п.
и т. п.
Пусть теперь надо (a – b – c + d) умножить на положительную дробь, напр., на +. Это все равно, что умножить на арифметическую дробь , что значит взять части от (a – b – c + d). Взять одну пятую часть от этого многочлена легко: надо (a – b – c + d) разделить на 5, а это уже умеем делать, – получим ![]() . Остается повторить полученный результат 3 раза или умножить на 3, т. е.
. Остается повторить полученный результат 3 раза или умножить на 3, т. е.
В результате мы видим, что пришлось каждый член многочлена умножить на или на +.
Пусть теперь надо (a – b – c + d) умножить на отрицательное число, целое или дробное,

т. е. и в этом случае пришлось каждый член многочлена умножить на –.
Таким образом, какое бы ни было число m, всегда (a – b – c + d) ∙ m = am – bm – cm + dm.
Так как каждый одночлен представляет собою число, то здесь мы видим указание, как умножать многочлен на одночлен – надо каждый член многочлена умножить на этот одночлен.

4. Умножение многочлена на многочлен . Пусть надо (a + b + c) ∙ (d + e). Так как d и e означают числа, то и (d + e) выражает какое-либо одно число.
(a + b + c) ∙ (d + e) = a(d + e) + b(d + e) + c(d + e)
(мы можем объяснить это и так: мы вправе d + e временно принять за одночлен).
Ad + ae + bd + be + cd + ce
В этом результате можно изменить порядок членов.
(a + b + c) ∙ (d + e) = ad + bd + ed + ae + be + ce,
т. е. для умножения многочлена на многочлен приходится каждый член одного многочлена умножать на каждый член другого. Удобно (для этого и был выше изменен порядок полученных членов) умножить каждый член первого многочлена сперва на первый член второго (на +d), затем на второй член второго (на +e), затем, если бы он был, на третий и т. д.; после этого следует сделать приведение подобных членов.

В этих примерах двучлен умножается на двучлен; в каждом двучлене члены расположены по нисходящим степеням буквы, общей для обоих двучленов. Подобные умножения легко выполнять в уме и сразу писать окончательный результат.
От умножения старшего члена первого двучлена на старший член второго, т. е. 4x² на 3x, получим 12x³ старший член произведения – ему подобных, очевидно, не будет. Далее мы ищем, от перемножения каких членов получатся члены с меньшею на 1 степенью буквы x, т. е. с x². Легко видим, что такие члены получатся от умножения 2-го члена первого множителя на 1-й член второго и от умножения 1-го члена первого множителя на 2-ой член второго (скобки внизу примера это указывают). Выполнить эти умножения в уме и выполнить также приведение этих двух подобных членов (после чего получим член –19x²) – дело нетрудное. Затем замечаем, что следующий член, содержащий букву x в степени еще на 1 меньшей, т. е. x в 1-ой степени, получится только от умножения второго члена на второй, и ему подобных не будет.
Еще пример: (x² + 3x)(2x – 7) = 2x³ – x² – 21x.
Также в уме легко выполнять примеры, вроде следующего:
Старший член получается от умножения старшего члена на старший, ему подобных членов не будет, и он = 2a³. Затем ищем, от каких умножений получатся члены с a² – от умножения 1-го члена (a²) на 2-ой (–5) и от умножения второго члена (–3a) на 1-ый (2a) – это указано внизу скобками; выполнив эти умножения и соединив полученные члены в один, получим –11a². Затем ищем, от каких умножений получатся члены с a в первой степени – эти умножения отмечены скобками сверху. Выполнив их и соединив полученные члены в один, получим +11a. Наконец, замечаем, что младший член произведения (+10), вовсе не содержащий a, получается от перемножения младшего члена (–2) одного многочлена на младший член (–5) другого.
Еще пример: (4a 3 + 3a 2 – 2a) ∙ (3a 2 – 5a) = 12a 5 – 11a 4 – 21a 3 + 10a 2 .
Из всех предыдущих примеров мы также получим общий результат: старший член произведения получается всегда от перемножения старших членов множителей, и подобных ему членов быть не может; также младший член произведения получается от перемножения младших членов множителей, и подобных ему членов также быть не может.
Остальным членам, получаемым при умножении многочлена на многочлен, могут быть подобные, и может даже случиться, что все эти члены взаимно уничтожатся, а останутся лишь старший и младший.
Вот примеры:
(a² + ab + b²) (a – b) = a³ + a²b + ab² – a²b – ab² – b³ = a³ – b³
(a² – ab + b²) (a – b) = a³ – a²b + ab² + a²b – ab² + b³ = a³ + b³
(a³ + a²b + ab² + b³) (a – b) = a 4 – b 4 (пишем только результат)
(x 4 – x³ + x² – x + 1) (x + 1) = x 5 + 1 и т. п.
Эти результаты достойны внимания и их полезно запомнить.
Особенно важен следующий случай умножения:
(a + b) (a – b) = a² + ab – ab – b² = a² – b²
или (x + y) (x – y) = x² + xy – xy – y² = x² – y²
или (x + 3) (x – 3) = x² + 3x – 3x – 9 = x² – 9 и т. п.
Во всех этих примерах, применяясь к арифметике, мы имеем произведение суммы двух чисел на их разность, а в результате получается разность квадратов этих чисел.
Если мы увидим подобный случай, то уже нет нужды выполнять умножение подробно, как это делалось выше, а можно сразу написать результат.
Напр., (3a + 1) ∙ (3a – 1). Здесь первый множитель, с точки зрения арифметики, есть сумма двух чисел: первое число есть 3a и второе 1, а второй множитель есть разность тех же чисел; потому в результате должно получиться: квадрат первого числа (т. е. 3a ∙ 3a = 9a²) минус квадрат второго числа (1 ∙ 1 = 1), т. е.
(3a + 1) ∙ (3a – 1) = 9a² – 1.
Также ![]()
(ab – 5) ∙ (ab + 5) = a²b² – 25 и т. п.
Итак, запомним
(a + b) (a – b) = a² – b²
т. е. произведение суммы из двух чисел на их разность равно разности квадратов этих чисел.
НР МОБУ «Пойковская средняя общеобразовательная школа №2»
Открытый урок по алгебре в 7 классе
по теме:
«Умножение одночлена на многочлен»
Учителя математики
Лимарь Т. А.
г. п. Пойковский, 2014
Методическая информация
Тип урока
Урок «открытия» нового знания
Цели урока (образовательные, развивающие, воспитательные)
Деятельностная цель урока : формирование у учащихся способностей к самостоятельному построению новых способов действия по теме «Умножение одночлена на многочлен» на основе метода рефлексивной самоорганизации.
Образовательная цель : расширение понятийной базы по теме «Многочлены» за счет включения в нее новых элементов: умножение одночленов на многочлен.
Задачи урока
образовательные:
Выработать алгоритм умножения одночлена на многочлен, рассмотреть примеры его применения.
развивающие:
Развитие внимания, памяти, умения рассуждать и аргументировать свои действия через решение проблемной задачи;
Развитие познавательного интереса к предмету;
Формирование эмоционально-положительного настроя у учащихся путем применения активных форм ведения урока и применением ИКТ;
Развитие рефлексивных умений через проведение анализа результатов урока и самоанализа собственных достижений.
воспитательные:
Развитие коммуникативных умений обучающихся через организацию групповой, парной и фронтальной работы на уроке.
Используемые методы
Словесные методы (беседа, чтение),
Наглядные (демонстрация презентации),
Проблемно-поисковый,
Метод рефлексивной самоорганизации (деятельностный метод),
Формирование личностных УУД.
Дидактическое обеспечение урока:
Компьютерная презентация,
Карточки с заданиями,
Карточки оценки работы на уроке,
Карточки с практическими заданиями по новой теме.
Этапы урок
Деятельность учителя
Деятельность учащихся
Организационный этап. (1мин)
Цели: актуализация знаний учащихся, определение целей урока, деление класса на группы (разно уровневые), выбор руководителя группы.
Психологический настрой, приветствие учащихся.
Приветствует учеников, называет эпиграф урока. Предлагает занять места по заранее распределенным группам и дает предварительный инструктаж.
Здравствуйте, присаживайтесь. Ребята, еще за тысячи лет до нашего рождения Аристотель говорил, что «…математика … выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного». И после каждого урока в мире математики неопределенности становится меньше. Я надеюсь, что и сегодня мы с вами откроем для себя что-то новое.
В ходе урока вы будете заполнять оценочный лист, который лежит у вас на столах, после выполнения каждого задания.
Учащиеся рассаживается по заранее разделенным группам. Знакомится с оценочным листом.
Устный счет.
Цель: проверить усвоение теоретического материала по теме: «Умножение одночлена на одночлен. Возведение в степень» и умения применять его на практике, развитие мыслительных навыков учащихся, осознание ценности совместной деятельности, борьба за успех группы.
а) математический диктант.
Привести подобные одночлены.
а) 2х+4у+6х=
б) -4а+в-3а=
в) 3c+2d+5d=
г) -2d +4a-3a =
2. Умножить одночлен на одночлен
а) -2ху 3х
б) (-4ав) (-2в)
г) (-5ав) (2z )
д) 2z (x +y )
Учитель предлагает выполнить математический диктант, записанный на доске. Контролирует правильность выполнение, подводит к изучению нового материала.
Совместно с учащимися формулирует цель и тему урока
- какой из номеров диктанта вызвал у вас наибольшие затруднения?
Давайте попробуем выяснить где именно возникло затруднение и почему?
- Цель нашего урока: научиться выполнять умножение одночлена на многочлен (справедливость вашего решения).
Тема урока: « У множение одночлена на многочлен».
Учащиеся выполняют задания. Совместно с учителем формулирует цель и тему урока. Записывают тему урока тетрадях.
(предполагаемый ответ учащихся д)
Выработать (сформулировать) правило умножения одночлена на многочлен.
Подведение к новой теме
Цель: подготовить учащихся к изучению нового материала.
Работа в группах.
Группа №1.
Вычислить.
15 80+15 20= 1200+300=1500
15 (80+20)=15 100=1500
Группа №2
Вычислить.
20 40+20 100=800+2000=2800
20 (40+100)=20 140=2800
Группа №3.
Вычислить .
6 (2а+3а)=6 5а=30а
6 2а+6 3а=12а+18а=30
Группа № 4
Вычислить
7 (4х+2х)= 7 6х=42
7 4х+7 2х=28х+14х=42х
Учитель проводит инструктаж. Контролирует выполнение.
Каждой группе необходимо найти значение двух выражений. Сравнить их и записать вывод в виде равенства или неравенства.
Учащиеся решают примеры в группах, делают вывод.
1 член от каждой группы пишет вывод на доске.
На доске написано:
15 80+15 20=15 (80+20)
20 40+20 100=20 (40+100)
6 (2а+3а)=6 2а+6 3
7 (4х+2х)=7 4х+7 2х
Учащиеся выставляют себе оценку в оценочный лист. Если вывод сформулирован и записан правильно, то ставят 5.
«Открытие» учащимися нового материала.
Цель:
формирование у учащихся способностей к самостоятельному построению новых способов действия по теме «Умножение одночлена на многочлен» на основе метода рефлексивной самоорганизации.
Выполнение задания «Заполните пропуски»
Слайд 2.
2z ∙(x +y )=2z ∙ +2z ∙
3х(а+в)= а+ в
Через минуту на доске высвечивается правильное решение.
Учитель дает инструктаж.
Проводит опрос. Делает вывод.
Пользуясь равенствами, записанными на доске, заполните пропуски в следующих выражениях
Обратите внимание, что стоит перед скобкой?
Что стоит в скобках?
Что получается в ответе?
И так, давайте сделаем вывод как умножить одночлен на многочлен. Через три минуты представляют свой материал классу (используется белый лист и фломастеры).
Обобщает
Проверим, правильно ли вы сформулировали правило. Для этого откроем учебник на стр.
Ученики работают в группах, каждая группа обсуждает, как заполнить пропуски.
Проверяют правильность заполнения пропусков.
Каждая группа выдвигает свою гипотезу и представляет классу, проходит общее обсуждение и делается вывод.
Читают вслух правило из учебника.
Одночлен
Многочлен
Первичное закрепление.
Цель: отработка навыков умножения одночлена на многочлен, развитие мыслительных навыков учащихся, осознание ценности совместной деятельности, борьба за успех группы, повышение мотивации учебной деятельности.
Работа в группах.
Группа №1, 3
х∙(
m ∙(n +3)=__________________ ; 7a ∙(2b -3c ) = _______________ ;
Группа №2, 4
a∙(c-y) = __________________ ; c∙(c+d)=___________________ ;
m∙(y+5)=__________________ ; 6m∙(2n-3k) = ______________ ;
7
Учитель дает инструктаж.
На парте возьмите карточку №2 Обязательное условие - при решении проговаривать друг другу правило.
Выполните взаимопроверку, группа 1 меняется карточками с группой 3, а группа 2 – с группой 4. Выставьте оценки группам в оценочный лист:
5 правильно выполненных задания – оценка «5»; 4 - «4»; 3- «3»; меньше 3- «2».
Выполняют задание на карточках, проводят взаимопроверку.
Ответственный член группы №1 спрашивает любого члена группы №3. Выставляет оценку в оценочный лист.
ответственный член группы №2 спрашивает любого члена группы №4. Выставляет оценку в оценочный лист
6. Математическая зарядка.
Цель: повысить или удержать умственную работоспособность детей на уроках;
обеспечить кратковременный активный отдых для учеников в течение урока.

Учитель проводит инструктаж, показывает карточки, на которых записаны одночлены, многочлены и выражения которые не являются ни одночленами, ни многочленами.
Учащиеся выполняют упражнения по командам
«Одночлен» - руки подняли вверх; «Многочлен» - руки перед собой «Другое выражение» - руки в стороны;
Закрыли глаза, про себя досчитали до 30, открыли глаза.
Математическое лото
Цель: закрепить алгоритм умножения одночлена на многочлен и побудить интерес к математике
Группа№1,3
с(3а-4в)=3ас-12вс;
3) 3c(x-3y)=3cx-9cy;
4) -n(x-m)=-nx+nm;
5) 3z (x-y )= 3zx-3zy .
Карточки с ответами:
3ас-12вс; 3ас+12вс; 3ас-4в
zx+2zy; zx-2zy; zx+2y;
3cx-9cy; 3cx+9cy; 3cx-3cy;
Nx+nm; nx+nm; nx-nm;
3zx-3zy; 3zx-y; zx-zy.
Группа №2, 4
Умножьте одночлен на многочлен
5a(b+3d)=5ab+15ad
А(3в+с)=-3ав-ас;
4x (5c -s )=20cx -4xs ;
a(3c+2b)=3ac +2ba
Карточки с ответами:
3ав-ас; 3ав+ас; в-ас;
20cx -4xs ; 20cx +4xs ; 5c -4xs ;
3ac+2ba; 3ac+6ba; 3ac-2ba;
cp-5cm; ср-5m; p-5cm.
5ab+ad; 5ab+5b; 5ab+15ad
Раздает конверты. Рассказывает правила игры. В одном конверте лежат 5 примеров на умножения одночлен на многочлен и 15 карточек с ответами.
Поясняю, как оценивать выполненную работу.
Группа получает оценку «5»,если первой выполнила все задания верно, 4 задания – «4»; 3 задания – «3», меньше трех –«2», та группа, которая завершает игру в лото второй, при этом выполнив все задания, верно получает оценку «4», третья – «3», последняя – «2».
Получают конверты с заданиями.
Выполняют умножение одночлена на одночлен.
Выбирают правильные ответы из всех предложенных карточек.
Самопроверка.
Получают карточку для самопроверки. Выставляют оценку в оценочный лист.
8 . Рефлексия учебной деятельности на уроке (итог урока).
Цель: самооценка учащимися результатов своей учебной деятельности, осознание метода построения границ и применения нового способа действия.
Фронтальная беседа по вопросы на слайде:
Какой алгоритм умножения одночлена на многочлен существует в математике?
Какой результат вашей деятельности?
Учитель проводит анализ оценочных листов (их результаты видны на слайде)
Возвращается к девизу урока, проводит параллель между эпиграфом и выведенном на уроке алгоритмом.
Сдайте оценочные листы, на которых четко видно результат вашей деятельности.
Еще раз вернемся к девизу нашего урока: «…математика … выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного». Алгоритм который мы вывели сегодня на уроке, поможет в дальнейшем сделать нам новые открытия: умножение многочлена на многочлен, поможет узнать формулы сокращенного умножения, о которых много говорят в алгебре. В переде нас ждет много интересного и важного.
Спасибо за урок!!!
Учащиеся делают самоанализ своей работы, вспоминают алгоритм, изученный на уроке, отвечают на вопросы.
ПРИЛОЖЕНИЕ.
КАРТОЧКА №1.
Группа №1.
Вычислить.
15 80+15 20= ______________________________
15 (80+20)= _______________________________
КАРТОЧКА №1.
Группа №2
Вычислить.
20 40+20 100 =_________________________________
20 (40+100)= __________________________________
КАРТОЧКА №1.
Группа №3.
Вычислить .
6 (2а+3а)=_____________________________________
6 2а+6 3а=_____________________________________
КАРТОЧКА №1
Группа № 4
Вычислить
7 (4х+2х)= _____________________________________
7 4х+7 2х= _____________________________________
КАРТОЧКА №2.
Группа №3
х∙(z +y ) = __________________ ; a ∙(c +d )=___________________ ;
5x∙(3a-6a)= _______ -________= _______.
КАРТОЧКА №4.
Группа №2
7x ∙(5d -8d )= ______ - ________= _______.КАРТОЧКА №2.
Группа №1
х∙(z +y ) = __________________ ; a ∙(c +d )=___________________ ;
m∙(n+3)=__________________ ; 7a∙(2b-3c) = _______________ ;
5x∙(3a-6a)= _______ -________= _______.
КАРТОЧКА №2.
Группа №2
a ∙(c -y ) = __________________ ; c ∙(c +d )=___________________ ;
m ∙(y +5)=__________________ ; 6m ∙(2n -3k ) = ______________ ;
7x ∙(5d -8d )= ______ - ________= _______.Математическое лото ( по два экземпляра)
с(3а-4в)
z(x+2y)
3c(x-3y)
-n(x-m)
3z (x-y )
-а(3в+с)
4x (5c -s )
a(3c+2b)
c(p-5m)
5a(b+3d)
Ответы к лото (по два экземпляра)
3ас-12вс
3ас+12вс
3ас-4в
zx+2zy;
zx-2zy
zx+2y
3сх-9су
3cx-3cy
3сх+3су
Nx+nm
nx+nm
nx-nm
zx-zy
3zx-y
3zx-3zy
3ав-ас
3ав+ас;
в-ас
20cx -4xs
20cx +4xs
5c -4xs
3ac+2ba
3ac+6ba
3ac-2ba
cp-5cm
ср-5m
p-5cm.
5ab+ad
5ab+5b