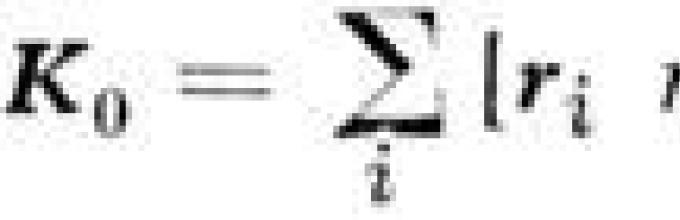МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
(кинетический
момент, момент импульса, орбитальный момент, угловой момент) - одна из динамич.
характеристик движения или механич. системы; играет особенно
важную роль при изучении вращат. движения. Как и для , различают
M. к. д. относительно центра (точки) и относительно оси.
M. к. д. материальной точки относительно центра
О
равен векторному произведению радиуса-вектора r
точки,
проведённого из центра О
, на её кол-во движения mv
, т. е. k
0
= [r
m
u
]
или в др. обозначениях k
0 = r
m
u
. M. к. д. k z
материальной точки относительно оси z, проходящей
через центр О
, равен проекции вектора k
0 на эту ось.
Для вычисления M. к. д. точки справедливы все ф-лы, приведённые для вычисления
момента силы
, если в них заменить вектор F
(или его проекции)
вектором m
u
(или его проекциями). Изменение M. к. д. точки происходит под действием
момента m
0 (F
) приложенной силы. Характер этого
изменения определяется ур-нием d
k
/dt = m
0 (F
),
являющимся следствием осн. закона . Когда m
0 (F
)
= 0, что, напр., имеет место для центр. сил, M. к. д. точки относительно центра
О
остаётся величиной постоянной; точка движется при этом по плоской кривой
и её радиус-вектор в любые равные промежутки времени описывает равные площади.
Этот результат важен для небесной механики (см. Кеплера законы
),а также
для теории движения космич. летат. аппаратов, ИСЗ и др.
Для механич. системы вводится понятие о главном
M. к. д. (или кинетич. моменте) системы относительно центра О
, равном
геом. сумме M. к. д. всех точек сис-темы относительно того же центра:![]()
Вектор K
0 может быть
определён его проекциями на взаимно перпендикулярные оси Oxyz
. Величины
K x , K y , К z
, являются одновременно главным
M. к. д. системы относительно соответствующих осей. Для тела, вращающегося вокруг
неподвижной оси z
с угл. скоростью w, эти величины равны: K x =
-I xz
w, К у = = -I yz
w,
K z = I z
w,
где I z
- осевой, a I xz
и I yz
- центробежные . Если же тело движется около неподвижной
точки О
, то для него в проекциях на главные оси инерции, проведённые
в точке О
, будет K x =- I x
w x ,
К у
= 1 у
w у,
K z = I z
w z
, где I x , 1 у, I z
- моменты инерции
относительно гл. осей; w x
, w y
, w z
- проекция мгновенной угл. скорости w
на эти оси. Из ф-л видно,
что направление вектора K
0 совпадает с направлением
w
лишь тогда, когда тело вращается вокруг одной из своих гл. (для
точки О
)осей инерции. В этом случае K
0 =
I
w
, где I
- момент инерции тела относительно этой
гл. оси.
Изменение главного M. к. д. системы происходит только в результате внеш. воздействий и зависит от гл. момента M e 0 внеш. сил; эта зависимость определяется ур-нием dK 0 /dt = M e 0 (ур-ние моментов). В отличие от случая движения одной точки, ур-ние моментов для системы не является следствием ур-ния кол-в движения, и оба эти ур-ния могут применяться для изучения движения системы одновременно. С помощью одного только ур-ния моментов движение системы (тела) может быть полностью определено лишь в случае чисто вращат. движения (вокруг неподвижной оси или точки). Если гл. момент внеш. сил относительно к--н. центра или оси равен нулю, то главный M. к. д. системы относительно этого центра или оси остаётся величиной постоянной, т. е. имеет место закон сохранения M. к. д. (см.
Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы все формулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv . Т. о.,k o = [r · mυ ], где r - радиус-вектор движущейся точки, проведённый из центра О , a k z равняется проекции вектора k o на ось z , проходящую через точку О . Изменение М. к. д. точки происходит под действием момента m o (F ) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой уравнением dk o /dt = m o (F ). Когда m о (F ) = 0, что, например, имеет место для центральных сил, движение точки подчиняется Площадей закону.
Главный М. к. д . (или кинетический момент) механической системы относительно центра О или оси z равен соответственно геометрической или алгебраической сумме М. к. д. всех точек системы относительно того же центра или оси, т. е. K o = Σk oi , K z = Σk zi . Вектор K o может быть определён его проекциями K x , K y , K z на координатные оси. Для тела, вращающегося вокруг неподвижной оси z с угловой скоростью ω, K x = - I xz ω, K y = -I yz ω, K z = I z ω, где l z - осевой, а I xz , l yz - центробежные моменты инерции.
Если ось z является главной осью инерции для начала координат О, то K o = I z ω.
Изменение главного М. к. д. системы происходит под действием только внешних сил и зависит от их главного момента M o e . Эта зависимость определяется теоремой об изменении главного М. к. д. системы, выражаемой уравнением dK o /dt = M o e . Аналогичным уравнением связаны моменты K z и M z e . Если M o e = 0 или M z e = 0, то соответственно K o или K z будут величинами постоянными, т. е. имеет место закон сохранения М. к. д.
Билет 20
Общее уравнение динамики.
Общее уравнение динамики – при движении системы с идеальными связями в каждый данный момент времен сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю. Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы. Дает общий метод решения задач динамики. Последовательность составления: а) к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силы и моменты пар сил инерции; б) сообщают системе возможные перемещения; в) составляют уравнения принципа возможных перемещений, считая систему находящейся в равновесии.
Потенциальная сила. Работа потенциальной силы на конечном перемещении.
Потенциальная сила - сила, работа которой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки
Работа потенциальной силы равна разности значений силовой функции в конечной и начальной точках пути и от вида траектории движущейся точки не зависит.
Основным свойством потенциального силового поля и является то, что работа сил поля при движении в нем материальной точки зависит только от начального и конечного положений этой точки и ни от вида ее траектории, ни от закона движения не зависит.
Билет 21
Принцип виртуальных (возможных) перемещений.
Существуют две различные формулировки принципа возможных перемещений. В одной формулировке утверждается, что для равновесия материальной системы необходимо, чтобы равнялась нулю сумма элементарных работ всех внешних сил, приложенных к системе, на любом возможном перемещении.
В другой формулировке, наоборот, говорится, что система должна находиться в равновесии, чтобы сумма элементарных работ всех сил равнялась нулю. Такое определение этого принципа дается, например, в работе: “Виртуальная работа заданных сил, приложенных к системе с идеальными связями и находящейся в равновесии, равна нулю”.
Математически принцип возможных перемещений представляется в виде:
, (1)
где - скалярное произведение вектора силы и вектора виртуального перемещения.
Мощность пары сил
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.
Мощность пары сил:
![]() ,
,
где омега Z – проекция угловой скорости на ось вращения.
Билет 22
1.Прнцип виртуальных перемещений
Рассмотрим виртуальное перемещение точки системы с номером i. Виртуальным перемещением δr i называется мысленное бесконечно малое перемещение точки, допускаемое связями без их разрушения в данное фиксированное мгновение времени.
Если связь одна и описывается уравнением (2), физически ясно, что связь не нарушится, когда вектор виртуального перемещения
где grad f - градиент функции (2) при фиксированном t , перпендикулярный поверхности связи в месте нахождения точки, равный
В вариационном исчислении бесконечно малые величины δr i , δx i , δy i , δz i называются вариациями функций r i , x i , y i , z i . Изменения координат точек или уравнений связи при неизменном времени находятся синхронным варьированием, которое осуществляется согласно левым частям формул (4) и (6).
То есть проекции δx i , δy i , δz i виртуального перемещения точки δr обращают в нуль первую вариацию уравнения связи при условии, что время не варьируется (синхронное варьирование):
| (7) |
Следовательно, виртуальное перемещение точки не характеризует ее движение, а определяет связь или, в общем случае, связи, наложенные на точку системы. Таким образом, виртуальные перемещения позволяют учесть эффект механических связей, не вводя реакции связей, как мы это делали раньше, и получать уравнения равновесия или движения системы в аналитическом виде, не содержащие неизвестных реакций связей.
2.Элементарная работа
Элементарная работа сил
, действующих на абсолютно твердое тело, равна алгебраической сумме двух слагаемых: работы главного вектора этих сил на элементарном поступательном перемещении тела вместе с произвольно выбранным полюсом и работы главного момента сил, взятого относительно полюса, на элементарном вращательном перемещении тела вокруг полюса. [1
]
Элементарная работа силы равна скалярному произведению силы на дифференциал радиуса-вектора точки приложения силы. [2 ]
Элементарная работа сил при этом зависит от выбора возможного перемещения системы. [3 ]
Элементарная работа силы при вращении тела, на которое сила действуе
Билет 23
1. Принцип виртуальных перемещений в обобщенных координатах.
Запишем принцип, выражая виртуальную работу активных сил системы в обобщенных координатах:
Так как на систему наложены голономные связи, вариации обобщенных координат не зависят между собой и не могут быть одновременно равны нулю. Поэтому последнее равенство выполнится только тогда, когда коэффициенты при δ j (j = 1 ÷ s) одновременно обращаются в нуль, то есть
2.Работа силы на конечном перемещении
Работа
силы на конечном перемещении определяется как интегральная сумма элементарных Работа
и при перемещении M
0 M
1 выражается криволинейным интегралом:
![]()
![]()
Билет 24
1.уравнение Лагранжа второго рода.
Для вывода уравнений запишем принцип Даламбера-Лагранжа в обобщенных координатах в виде -Q j u = Q j (j = 1 ÷ s) .
Принимая во внимание, что Ф i = -m i a i = -m i dV i / dt , получаем:
 (1)
(1)
 (2)
(2)
Подставляя (2) в (1) получаем дифференциальное уравнение движения системы в обобщенных координатах, которое названо уравнением Лагранжа второго рода:
 (3)
(3)
то есть, материальная система с голономными связями описывается уравнениями Лагранжа второго рода по всем s обобщенным координатам.
Отметим важные особенности полученных уравнений.
1. Уравнения (3) - это система обыкновенных дифференциальных уравнений второго порядка относительно s неизвестных функций q j (t), полностью определяющих движение системы.
2. Число уравнений равно числу степеней свободы, то есть движение любой голономной системы описывается наименьшим числом уравнений.
3. В уравнения (3) не нужно включать реакции идеальных связей, что позволяет, находя закон движения несвободной системы, выбором обобщенных координат исключить задачу определения неизвестных реакций связей.
4. Уравнения Лагранжа второго рода позволяют указать единую последовательность действий для решения многих задач динамики, которую часто называют формализмом Лагранжа.
2. Условие относительного покоя материальной точки получают из динамического уравнения Кориолиса, подставив в это уравнение значения относительного ускорения и кориолисовой силы инерции равные нулю:

![]()
момент количества движения
МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ (кинетический момент, момент импульса, угловой момент) мера механического движения тела или системы тел относительно какого-либо центра (точки) или оси. Для вычисления момента количества движения К материальной точки (тела) справедливы те же формулы, что и для вычисления момента силы, если заменить в них вектор силы на вектор количества движения mv, в частности K0 = . Сумма моментов количества движения всех точек системы относительно центра (оси) называется главным моментом количества движения системы (кинетическим моментом) относительно этого центра (оси). При вращательном движении твердого тела главный момент количества движения относительно оси вращения z тела выражается произведением момента инерции Iz на угловую скорость? тела, т.е. КZ = Iz?.
Момент количества движения
кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращательного движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и относительно оси.
Для вычисления М. к. д. k материальной точки относительно центра О или оси z справедливы все формулы, приведённые для вычисления момента силы, если в них заменить вектор F вектором количества движения mv. Т. о., ko = , где r ≈ радиус-вектор движущейся точки, проведённый из центра О, a kz равняется проекции вектора ko на ось z, проходящую через точку О. Изменение М. к. д. точки происходит под действием момента mo(F) приложенной силы и определяется теоремой об изменении М. к. д., выражаемой уравнением dko/dt = mo(F). Когда mо(F) = 0, что, например, имеет место для центральных сил, движение точки подчиняется площадей закону. Этот результат важен для небесной механики, теории движения искусственных спутников Земли, космических летательных аппаратов и др.
Главный М. к. д. (или кинетический момент) механической системы относительно центра О или оси z равен соответственно геометрической или алгебраической сумме М. к. д. всех точек системы относительно того же центра или оси, т. е. Ko = Skoi, Kz = Skzi. Вектор Ko может быть определён его проекциями Kx, Ky, Kz на координатные оси. Для тела, вращающегося вокруг неподвижной оси z с угловой скоростью w, Kx = ≈ Ixzw, Ky = ≈Iyzw, Kz = Izw, где lz ≈ осевой, а Ixz, lyz ≈ центробежные моменты инерции. Если ось z является главной осью инерции для начала координат О, то Ko = Izw.
Изменение главного М. к. д. системы происходит под действием только внешних сил и зависит от их главного момента Moe. Эта зависимость определяется теоремой об изменении главного М. к. д. системы, выражаемой уравнением dKo/dt = Moe. Аналогичным уравнением связаны моменты Kz и Mze. Если Moe = 0 или Mze = 0, то соответственно Ko или Kz будут величинами постоянными, т. е. имеет место закон сохранения М. к. д. (см. Сохранения законы). Т. о., внутренние силы не могут изменить М. к. д. системы, но М. к. д. отдельных частей системы или угловые скорости под действием этих сил могут изменяться. Например, у вращающегося вокруг вертикальной оси z фигуриста (или балерины) величина Kz= Izw будет постоянной, т. к. практически Mze = 0. Но изменяя движением рук или ног значение момента инерции lz, он может изменять угловую скорость w. Др. примером выполнения закона сохранения М. к. д. служит появление реактивного момента у двигателя с вращающимся валом (ротором). Понятие о М. к. д. широко используется в динамике твёрдого тела, особенно в теории гироскопа.
Размерность М. к. д. ≈ L2MT-1, единицы измерения ≈ кг×м2/сек, г×см2/сек. М. к. д. обладают также электромагнитное, гравитационное и др. физические поля. Большинству элементарных частиц присущ собственный, внутренний М. к. д. ≈ спин . Большое значение М. к. д. имеет в квантовой механике.
Лит. см. при ст. Механика.
Момент количества движения материальной точки относительно некоторого центра О равен векторному произведению радиуса-вектора движущейся точки на количество движения , т. е.
![]()
Очевидно, что модуль момента количества движения равен
![]()
где - плечо вектора v относительно центра О (рис. 167).
Проектируя векторное равенство (153) на координатные оси, проходящие через центр О, получаем формулы для моментов количества движения материальной точки относительно этих осей:
В векторной форме теорема о моменте количества движения выражается так: производная по времени от момента количества движения материальной точки относительно какого-либо неподвижного центра О равна моменту действующей силы относительно того же центра, т. е.
![]()
Проектируя векторное равенство (156) на какую-либо из координатных осей, проходящих через центр О, получаем уравнение, выражающее ту же теорему в скалярной форме:
![]()
т. е. производная по времени от момента количества движения материальной точки относительно какой-либо неподвижной оси равна моменту действующей силы относительно той же оси.


Эта теорема имеет большое значение при решении задач в случае движения точки под действием центральной силы Центральной силой называется такая сила, линия действия которой все время проходит через одну и ту же точку, называемую центром этой силы. Если материальная точка движется под действием центральной силы F с центром в точке О, то
![]()
и, следовательно, . Таким образом, момент количества движения в данном случае остается постоянным по модулю и по направлению. Отсюда следует, что материальная точка под действием центральной силы описывает плоскую кривую, расположенную в плоскости, проходящей через центр силы.
Если известна траектория, которую описывает точка под действием центральной силы, то, пользуясь теоремой о моменте количества движения, можно найти эту силу как функцию расстояния от точки до центра силы.
Действительно, так как момент количества движения относительно центра силы остается постоянным, то, обозначая h плечо вектора относительно центра силы, имеем:
![]() (158)
(158)
Для определения этой постоянной должна быть известна скорость точки в каком-либо месте траектории. С другой стороны, имеем (рис. 168):
![]()
где - радиус кривизны траектории, - угол между радиусом-вектором точки и касательной к траектории в этой точке.
Итак, имеем два уравнения (158) и (159) с двумя неизвестными v и F; остальные величины, входящие в эти уравнения, т. е. , являясь элементами заданной траектории, легко могут быть найдены. Таким образом, можно найти v и F как функции .
Пример 129. Точка М описывает эллипс под действием центральной силы F (рис. 169). Скорость в вершине А равна . Найти скорость в вершине В, если и .

Решение. Так как в данном случае
Пример 130. Точка М массы описывает окружность радиуса а, притягиваясь точкой А этой окружности (рис. 170).
Количество движения (mV) - величина векторная, т.е. имеет определенное направление относительно выбранной точки отсчета (например, оси координат) или оси вращения. Основное уравнение динамики вращательного движения
можно также записать в виде
Здесь С/оо) имеет смысл аналога физической величины (mV) количества движения. Силовой момент М = Ph тогда с учетом (7.14)
Величину L можно рассматривать как момент количества движения (mV) относительно данной точки или оси. Она называется кинетическим моментом. Здесь h - кратчайшее расстояние от линии действия вектора mV по часовой стрелке. В общем случае
![]()
Знак «-» берется в случае вращения вектора mV по часовой стрелке.
Для пространственной системы момент количества движения материальной точки относительно оси, перпендикулярной к данной плоскости и проходящей через заданную точку 0, равен проекции момента количества движения. Например, для оси z: L z = L 0 cos а, где а - угол между данной плоскостью и радиус-вектором данной точки (расстояние от материальной точки до центра «0»).
Величина L относительно прямоугольных осей координат определяется проекциями скоростей на эти оси и координатами движущейся материаль-

Рис. 7.1.
ной точки. Например, в плоскости хОу (рис. 7.1) момент количества движения относительно оси z (перпендикулярной данной плоскости)

здесь L, и L 2 - моменты, создаваемые проекциями количества движения mV относительно точки 0.
По физическому смыслу производная - сумма моментов сил,
действующих на материальную точку, относительно выбранной оси координат. При JM i = 0, величина L = const, т.е. если момент равнодействующей силы равен нулю , то момент количества движения относительно выбранной оси остается постоянным.

Рис. 7.2.
Например, для точечного тела М с массой т величина L z = 0, если на тело действует сила Р, направленная к началу координат, так как моменты силы Р и силы тяжести mg (параллельной оси z, рис. 7.2) равны нулю. Здесь L z = mxV = const.
Если направление скорости V 0 все время перпендикулярно радиусу г, величина которого при перемещении точки М 2 уменьшается, то из равенства L z = const следует увеличение скорости точки М при приближении к точке О.
По аналогии с главным моментом сил можно вывести понятие: главный момент количества движения i 0 механической системы (или кинетический момент), относительно заданного центра, который равен геометрической сумме величин L 0j всех материальных точек данной системы относительно этого центра, т.е.
Кинетический момент механической системы относительно оси (например оси г) равен алгебраической сумме моментов количества движения всех точек данной системы: L 0 = X L iz .
Очевидно, что производная от кинетического момента по времени равна главному моменту внешних сил, действующих на данную механическую систему (относительно выбранного центра), т.е.
Отсюда следует закон сохранения кинетического момента механической системы относительно оси
т.е. кинетический момент в данном случае остается постоянным.
Изменения кинетического момента механической системы при ударе вытекает как следствие из рассмотрения вышеизложенных понятий об импульсе силы и моментах количества движения и определяется выражениями (7.17) и (7.18). Так, например, при ударе изменение кинетического момента системы относительно любой оси равно сумме моментов внешних импульсов сил относительно данной оси. Если к точкам механической системы приложены только внутренние силовые импульсы, то кинетический момент системы при ударе не изменяется.