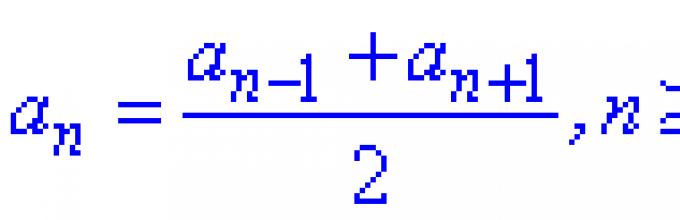Арифметической прогрессией называют последовательность чисел (членов прогрессии)

В которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии .

Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле

Свойства арифметической прогрессии

1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии

Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией. По этим утверждением очень просто проверить любую последовательность.

Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей

В этом легко убедиться, если расписать слагаемые справа от знака равенства

Ее часто применяют на практике для упрощения вычислений в задачах.

2) Сумма n первых членов арифметической прогрессии вычисляется по формуле

Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.

3) Если нужно найти не всю сумму, а часть последовательности начиная с k -го ее члена, то в Вам пригодится следующая формула суммы

4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k -го номера. Для этого используйте формулу

На этом теоретический материал заканчивается и переходим к решению распространенных на практике задач.

Пример 1. Найти сороковой член арифметической прогрессии 4;7;...

Решение:

Согласно условию имеем

Определим шаг прогрессии

По известной формуле находим сороковой член прогрессии

Пример2. Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.

Решение:

Распишем заданные элементы прогрессии по формулам

От второго уравнения вычтем первое, в результате найдем шаг прогрессии

Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии

Вычисляем сумму первых десяти членов прогрессии

Не применяя сложных вычислений ми нашли все искомые величины.

Пример 3. Арифметическую прогрессию задано знаменателем и одним из ее членов . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.

Решение:

Запишем формулу сотого элемента прогрессии

и найдем первый

На основе первого находим 50 член прогрессии

Находим сумму части прогрессии

и сумму первых 100

Сумма прогрессии равна 250.

Пример 4.

Найти число членов арифметической прогрессии, если:

а3-а1=8, а2+а4=14, Sn=111.

Решение:

Запишем уравнения через первый член и шаг прогрессии и определим их

Полученные значения подставляем в формулу суммы для определения количества членов в сумме

Выполняем упрощения

и решаем квадратное уравнение

Из найденных двух значений условии задачи подходит только число 8 . Таким образом сумма первых восьми членов прогрессии составляет 111.

Пример 5.

Решить уравнение

1+3+5+...+х=307.

Решение: Данное уравнение является суммой арифметической прогрессии. Выпишем первый ее член и найдем разницу прогрессии

В математике любая организованная каким-либо способом совокупность чисел, которые следуют друг за другом, называется последовательностью. Из всех существующих последовательностей чисел выделяют два интересных случая: прогрессии алгебраическую и геометрическую.

Что представляет собой арифметическая прогрессия?

Сразу следует сказать, что алгебраическую прогрессию часто называют арифметической, поскольку ее свойства изучает ветвь математики - арифметика.

Эта прогрессия представляет собой такую последовательность чисел, в которой каждый следующий ее член отличается от предыдущего на некоторое постоянное число. Оно называется разностью алгебраической прогрессии. Для определенности обозначим его латинской буквой d.

Примером такой последовательности может быть следующая: 3, 5, 7, 9, 11 ..., здесь видно, что число 5 больше числа 3 на 2, 7 больше 5 тоже на 2, и так далее. Таким образом, в представленном примере d = 5-3 = 7-5 = 9-7 = 11-9 = 2.

Какие бывают арифметические прогрессии?

Характер этих упорядоченных последовательностей чисел во многом определяется знаком числа d. Выделяют следующие виды алгебраических прогрессий:

возрастающая, когда d положительное (d>0);
постоянная, когда d = 0;
убывающая, когда d отрицательное (d<0).

В примере, который приведен в предыдущем пункте, показана возрастающая прогрессия. Примером убывающей является следующая последовательность чисел: 10, 5, 0, -5, -10, -15 ... Постоянная прогрессия, как следует из ее определения, представляет собой совокупность одинаковых чисел.

n-й член прогрессии

Благодаря тому, что каждое последующее число в рассматриваемой прогрессии отличается на константу d от предыдущего, можно легко определить n-й ее член. Для этого нужно знать не только d, но и a 1 - первый член прогрессии. Применяя рекурсивный подход, можно получить формулу алгебраической прогрессии для нахождения n-го члена. Она имеет вид: a n = a 1 + (n-1)*d. Это формула является достаточно простой, и понять ее можно на интуитивном уровне.

Также не представляет никакой сложности ее использование. Например, в прогрессии, которая приведена выше (d=2, a 1 =3), определим 35-й ее член. Согласно формуле, он будет равен: a 35 = 3 + (35-1)*2 = 71.

Формула для суммы

Когда дана некоторая арифметическая прогрессия, то сумма ее первых n членов является часто возникающей задачей, наряду с определением значения n-го члена. Формула суммы алгебраической прогрессии записывается в следующем виде: ∑ n 1 = n*(a 1 +a n)/2, здесь значок ∑ n 1 говорит о том, что суммируются с 1-го по n-й член.

Приведенное выражение можно получить, прибегая к свойствам все той же рекурсии, однако существует более легкий способ доказательства его справедливости. Запишем первые 2 и последние 2 члена этой суммы, выразив их в числах a 1 , a n и d, и получим: a 1 , a 1 +d,...,a n -d, a n . Теперь заметим, что если сложить первый член с последним, то он будет точно равен сумме второго и предпоследнего члена, то есть a 1 +a n . Аналогичным способом можно показать, что эту же сумму можно получить, если сложить третий и предпредпоследний члены, и так далее. В случае парного количества чисел в последовательности получаем n/2 сумм, каждая из которых равна a 1 +a n . То есть получаем вышеприведенную формулу алгебраической прогрессии для суммы: ∑ n 1 = n*(a 1 +a n)/2.

Для непарного количества членов n получается аналогичная формула, если следовать описанным рассуждениям. Только нужно не забыть добавить оставшееся слагаемое, которое находится в центре прогрессии.

Покажем, как пользоваться приведенной формулой на примере простой прогрессии, которая была введена выше (3, 5, 7, 9, 11 ...). Например, необходимо определить сумму первых 15 ее членов. Для начала определим a 15 . Воспользовавшись формулой для n-го члена (см. предыдущий пункт), получаем: a 15 = a 1 + (n-1)*d = 3 + (15-1)*2 = 31. Теперь можно применить формулу суммы алгебраической прогрессии: ∑ 15 1 = 15*(3+31)/2 = 255.

Любопытно привести интересный исторический факт. Формулу для суммы арифметической прогрессии впервые получил Карл Гаусс (знаменитый немецкий математик XVIII века). Когда ему было всего 10 лет, то учитель задал задачу, найти сумму чисел от 1 до 100. Говорят, что маленький Гаусс решил эту задачу за несколько секунд, заметив, что попарно суммируя числа с начала и конца последовательности, всегда можно получить 101, а поскольку таких сумм 50, то он быстро выдал ответ: 50*101 = 5050.

Пример решения задачи

В качестве завершения темы алгебраической прогрессии приведем пример решения еще одной любопытной задачи, закрепив тем самым понимание рассматриваемой темы. Пусть дана некоторая прогрессия, для которой известна разность d = -3, а также ее 35-й член a 35 = -114. Необходимо найти 7-й член прогрессии a 7 .

Как видно из условия задачи, значение a 1 является неизвестным, поэтому напрямую формулой для n-го члена воспользоваться не получится. Также является неудобным способ рекурсии, который в ручную тяжело реализовать, и велика вероятность допустить ошибку. Поступим следующим образом: выпишем формулы для a 7 и a 35 , имеем: a 7 = a 1 + 6*d и a 35 = a 1 + 34*d. Вычтем из первого выражения второе, получим: a 7 - a 35 = a 1 + 6*d - a 1 - 34*d. Откуда следует: a 7 = a 35 - 28*d. Осталось подставить известные данные из условия задачи и записать ответ: a 7 = -114 - 28*(-3) = -30.

Геометрическая прогрессия

Чтобы раскрыть тему статьи полнее, приведем краткое описание еще одного вида прогрессии - геометрической. В математике под этим названием понимают последовательность чисел, в которой каждый последующий член отличается от предыдущего на некоторый множитель. Обозначим этот множитель буквой r. Он называется знаменателем рассматриваемого вида прогрессии. Примером этой последовательности чисел может быть следующая: 1, 5, 25, 125, ...

Как видно из приведенного определения, алгебраическая и геометрическая прогрессии схожи по своей идее. Отличие между ними заключается в том, что первая изменяется медленнее, чем вторая.

Геометрическая прогрессия также может быть возрастающей, постоянной и убывающей. Ее тип зависит от значения знаменателя r: если r>1, то имеет место возрастающая прогрессия, если r<1 - убывающая, наконец, если r = 1 - постоянная, которая в этом случае может также называться постоянной арифметической прогрессией.

Формулы геометрической прогрессии

Как и в случае алгебраической, формулы геометрической прогрессии сводятся к определению ее n-го члена и суммы n слагаемых. Ниже приведены эти выражения:

a n = a 1 *r (n-1) - эта формула следует из определения геометрической прогрессии.
∑ n 1 = a 1 *(r n -1)/(r-1). Важно отметить, если r = 1, то приведенная формула дает неопределенность, поэтому ей пользоваться нельзя. В этом случае сумма n членов будет равна простому произведению a 1 *n.

Например, найдем сумму всего 10 членов последовательности 1, 5, 25, 125, ... Зная, что a 1 = 1 и r = 5, получаем: ∑ 10 1 = 1*(5 10 -1)/4 = 2441406. Полученное значение является наглядным примером того, насколько быстро растет геометрическая прогрессия.

Пожалуй, первым упоминанием об этой прогрессии в истории является легенда с шахматной доской, когда друг одного султана, обучив его игре в шахматы, попросил за свою услугу зерно. Причем количество зерна должно было быть следующим: на первую клетку шахматной доски необходимо положить одно зерно, на вторую в два раза больше, чем на первую, на третью в 2 раза больше, чем на вторую и так далее. Султан охотно согласился выполнить эту просьбу, но он не знал, что ему придется опустошить все закрома своей страны, чтобы сдержать данное слово.

Примеры на арифметическую и геометрическую прогрессию взяты из "Сборника задач для абитуриентов. Математика" изданного Волынским государственным университетом имени Леси Украинки в 2001 году. Внимательно ознакомьтесь с ответами и выберите для себя самое необходимое.

Группа А (уровень 1)

Пример 1. Вычислить шестой член арифметической прогрессии 21,3; 22,4; … ,
Решение: Найдем разницу (шаг) прогрессии
d=a 2 -a 1 =22,4-21,3=1,1.
Далее вычисляем шестой член арифметической прогрессии
a 6 =a 1 +(6-1)d=21,3+5*1,1=26,8.

Пример 2. Вычислить шестой член геометрической прогрессии 5; 10; 20; ...
Решение: Найдем знаменатель геометрической прогрессии
q=b 2 /b 1 =10/5=2.
Вычисляем шестой член геометрической прогрессии
b 6 =b 1 q 6-1 =5*25=5*32=160.

Пример 3. В арифметической прогрессии a 1 =2,1 a 10 =12,9 . Вычислить разницу прогрессии.
Решение: Представим десятый член прогрессии в виде формулы
a 10 =a 1 +(10-1)d= a 1 +9d .
Подставим известные значения и решим
12,9=2,1+9d;
9d=12,9-2,1=10,8;
d=10,8/9=1,2.
Ответ: разница прогрессии d=1,2.

Пример 4. В геометрической прогрессии b 1 =2,56; b 4 =4,42368. Вычислить знаменатель прогрессии.
Решение: Находим знаменатель прогрессии
q=b 2 /b 1 =4,42368/2,56=1,728.
Без калькулятора здесь не обойтись.
Ответ: знаменатель прогрессии равен q=1,728.

Пример 5. В арифметической прогрессии a 1 =20,1, d=1,3 . Вычислить сумму первых восьми членов прогрессии.
Решение: Cуму арифметической прогрессии находим по формуле

Выполняем вычисления
S 8 =(2*20,1+(8-1)*1,3)*8/2=197,2.
Ответ: S 8 =197,2 .

Пример 6 . В геометрической прогрессии b 1 =1,5; q=1,2 . Вычислить сумму первых четырех членов прогрессии.
Решение: Cуму геометрической прогрессии вычисляем по формуле

Находим сумму прогрессии

Ответ: S 8 =8,052.

Пример 7 . В арифметической прогрессии a 1 =1,35 d=-2,4 . Вычислить номер члена прогрессии, равный -25,05.
Решение: Член арифметической прогрессии находят по формуле
a n =a 1 +(n-1)d.
По условию задано все кроме порядкового номера известно, найдем его
-25,05=1,35+(n-1)(-2,4) ;

Ответ: n=12.

Пример 8. Вычислить седьмой член прогрессии 23,5; 24,82; 26,14; ...
Решение: Поскольку в условии не задано какая прогрессия задана, то сначала нужно ето установить. Получите, что арифметическая
d=a 2 -a 1 =24,82-23,5=1,32;
d=a 3 -a 2 =26,14-24,82=1,32.
Находим седьмой член прогрессии
a 7 =a 1 +(7-1)d=23,5+6*1,32=31,42.
Ответ: a 7 = 31,42.

Пример 9. Вычислить номер члена прогрессии 2,1; 3,3; 4,5; ... , равный 11,7 .
Решение: Легко убедиться, что задана арифметическая прогрессия. Найдем разницу прогрессии
d=a 2 -a 1 =3,3-2,1=1,2.
По формуле члена прогрессии
a n =a 1 +(n-1)d
найдем номер
11,7=2,1+(n-1)*1,2;

Ответ: n= 9 .

Пример 10. Вычислить четвертый член прогрессии 1,5; 1,8; 2,16; ... .
Решение: Без проверки можно сказать, что прогрессия - геометрическая. Найдем ее знаменатель
q=b 2 /b 1 =1, 8/1,5=1,2.
Вычислим 4 член геометрической прогрессии по формуле
b 4 =b 1 q 3 =1,5*1,2 3 =2,592.
Ответ: b 4 =2,592 .

Пример 11. Вычислить номер члена прогрессии 1,2; 1,8; 2,16; ... равный 4,05.
Решение: Имеем геометрическую прогрессию. Найдем знаменатель прогрессии
q=b 2 /b 1 =1, 8/1,2=1,5.
Найдем номер прогресии из зависимости
b n =b 1 q n-1 .
4,05=1,2*1,5 n-1 ;
1,5 n-1 =4,05/1,2=3,375=1,5 3 ;
n-1=3; n=4.
Ответ: n=4.

Пример 12. В арифметической прогрессии a 5 =14,91 a 9 =20,11. Вычислить a 1 .
Решение: Выразим 9 член прогрессии через 5
a 9 = a 5 +(9-5)d
и найдем шаг прогрессии
20,11=14,91+4d;
4d=5,2; d=5,2/4=1,3.
Выразим 5 член прогрессии через 1 и вычислим первый
a 5 = a 1 +4d;
14,91= a 1 +5,2;
a 1 =14,91-5,2=9,71.
Ответ: a 1 =9,71.

Пример 13 . В арифметической прогрессии а 7 =12,01; a 11 =17,61. Вычислить разницу прогрессии.
Решение: Выразим 11 член прогрессии через 7
a 11 = a 7 +(11-7)d.
Отсюда вычислим шаг прогрессии
17,61=12,01+4d;
4d=5,6; d=5,6/4=1,4.
Ответ: d=1,4.

Пример 14. В геометрической прогрессии b 5 =64; b 8 =1. Вычислить b 3 .
Решение: Выразим 8 член прогрессии через 5
b 8 = b 5 q 8-5 .
Отсюда находим знаменатель прогрессии
1=64 q 3 ;
q 3 =1/64=(1/4) 3 ;
q=1/4.
Подобным образом находим b 3 через b 5
b 3 = b 5 /q 2 =64*4 2 =1024.
Ответ: b 3 =1024.

Пример 15. В арифметической прогрессии а 9 +а 15 =14,8 . Вычислить а 12
Решение: В этом примере следует учесть, что 12 член прогрессии находится посередине между 9 ее номером и 15 . Поэтому соседние члены прогрессии (9, 15 ) можно выразить через 12 следующим образом
a 9 = a 12 -(12-9)d;
a 15 = a 12 +(15-9)d;
a 9 = a 12 -3d;
a 15 = a 12 +3d.
Просуммируем крайние члены прогрессии
a 9 + a 15 = a 12 -3d+ a 12 +3d=2a 12 .
Отсюда находим 12 член прогрессии
a 12 =(a 9 +a 15)/2=14,8/2=7,4.
Ответ: a 12 =7,4.

Пример 16. В геометрической прогрессии b 10 *b 14 =289. Вычислить модуль 12 члена прогрессии | b 12 |.
Решение: Алгоритм решении задачи содержится в предыдущем примере. Следует выразить 10 и 14 член геометрической прогрессии через 12 . По свойствам геометрической прогрессии получим
b 10 = b 12 /q 2 ; b 14 = b 12 *q 2 .
Легко заметить, что при их произведения знамениик прогрессии пропадает
b 10 * b 14 = (b 12) 2 =289=17 2 .
Отсюда находим модуль | b 12 |
(b 12) 2 =289=17 2 -> | b 12 |=17.
Ответ: | b 12 |=17.

Пример 17. В геометрической прогрессии b 8 =1,3. Вычислить b 6 *b 10 .
Решение: Схема вычислений аналогична предыдущему примеру - выражаем 6 и 10 член прогрессии через 8.
b 6 = b 8 /q 2 ; b 10 = b 8 *q 2 .
При их умножении знаменатели сокращаются и получим квадрат известного члена прогрессии
b 6 *b 10 = (b 8) 2 =1,3 2 =1,69.
Ответ: b 6 *b 10 =1,69.

Пример 18. В арифметической прогрессии а 10 =3,6: a 12 =8. Вычислить а 8
Решение: Запишем члены прогрессии в ряд а 8 , а 10 , a 12 . Между ними одинаковый шаг, найдем его
a 12 = a 10 +2d;
2d= a 12 - a 10 =8-3,6=4,4.
Таким же методом находим а 8
a 10 = a 8 +2d;
a 8 = a 10 -2d=3,6-4,4=-0,8.
Вот такие несложные расчеты.
Ответ: a 8 =-0,8.

Пример 19. В геометрической прогрессии b 14 =8; b 16 =2. Вычислить b 12 .
Решение: Опуская подробные объяснения, запишем произведение 14 и 16 члена прогрессии
b 14 *b 16 =(b 12) 2 .
Это равносильно среднему геометрическому. Найдя корень из произведения членов, получим искомое значение
(b 12) 2 =8*2=16; b 12 =4.
Ответ: b 12 =4.

Пример 20. В арифметической прогрессии а 5 =3,4; a 11 =6,9. Вычислить а 17 .
Решение: Между 5,11 и 17 членом прогрессии одинаковый шаг и он равен 6d . Поэтому конечное решение можно записать в виде
а 17 = a 11 +6d= a 11 +(a 11 - а 5)=2*6,9-3,4=10,4.
Думаю, что Вы понимаете, почему такая запись. Если нет - попробуйте расписать 11 член прогрессии через 5 и виразить 6d .
Ответ: а 17 =10,4 .

Пример 21. Вычислить 6-й член геометрической прогрессии 3; 12;... .
Решение: Найдем знаменатель прогрессии
q=b 2 /b 1 =12/3=4.
Воспользуемся общей формуле члена геометрической прогрессии
b n = b 1 *q n-1 .
Отсюда получим
b 6 = b 1 *q 5 =b 2 *q 4 .
Как видите, главное в записи, чтобы сумма индекса (2) и степень (4) соответствовала порядковому номеру члена прогрессии (6). Выполняем вычисления
b 6 = 12*4 4 =12*256=3072.
Получили большое число, но геометрическая прогрессия тем и отличается, что ее члены или быстро растут, или - сходят.
Ответ: b 6 =3072.

Пример 22. В арифметической прогрессии а 3 =48; a 5 =42. Вычислить а 7 .
Решение: Так как разница прогрессии между заданными членами и искомым сталая и равна 2d то формула 7 члена прогрессии будет выглядеть
а 7 = a 5 +2d= a 5 +(a 5 - а 3);
а 7 =2*42-48=36 .
Ответ: а 7 =36.

Задачи по арифметической прогрессии существовали уже в глубокой древности. Они появлялись и требовали решения, поскольку имели практическую необходимость.

Так, в одном из папирусов Древнего Египта, имеющем математическое содержание, - папирусе Райнда (XIX век до нашей эры) - содержится такая задача: раздели десять мер хлеба на десять человек, при условии если разность между каждым из них составляет одну восьмую меры».

И в математических трудах древних греков встречаются изящные теоремы, имеющие отношение к арифметической прогрессии. Так, Гипсикл Александрийский (II век составивший немало интересных задач и добавивший четырнадцатую книгу к «Началам» Евклида, сформулировал мысль: «В арифметической прогрессии, имеющей четное число членов, сумма членов 2-ой половины больше суммы членов 1-ой на квадрату 1/2 числа членов».

Обозначается последовательность an. Числа последовательности называются ее членами и обозначаются обычно буквами с индексами, которые указывают порядковый номер этого члена (a1, a2, a3 … читается: «a 1-ое», «a 2-ое», «a 3-тье» и так далее).

Последовательность может быть бесконечной или конечной.

А что же такое арифметическая прогрессия? Под ней понимают получаемую сложением предыдущего члена (n) с одним и тем же числом d, являющимся разностью прогрессии.

Если d<0, то мы имеем убывающую прогрессию. Если d>0, то такая прогрессия считается возрастающей.

Арифметическая прогрессия называется конечной, если учитываются только несколько ее первых членов. При очень большом количестве членов это уже бесконечная прогрессия.

Задается любая арифметическая прогрессия следующей формулой:

an =kn+b, при этом b и k - некоторые числа.

Абсолютно верно утверждение, являющееся обратным: если последовательность задается подобной формулой, то это точно арифметическая прогрессия, которая имеет свойства:

Каждый член прогрессии - среднее арифметическое предыдущего члена и последующего.
Обратное: если, начиная со 2-ого, каждый член - среднее арифметическое предыдущего члена и последующего, т.е. если выполняется условие, то данная последовательность - арифметическая прогрессия. Это равенство одновременно является и признаком прогрессии, поэтому его, как правило, называют характеристическим свойством прогрессии.
Точно так же верна теорема, которая отражает это свойство: последовательность - арифметическая прогрессия только в том случае, если это равенство верно для любого из членов последовательности, начиная со 2-ого.

Характеристическое свойство для четырёх любых чисел арифметической прогрессии может быть выражено формулой an + am = ak + al, если n + m = k + l (m, n, k - числа прогрессии).

В арифметической прогрессии любой необходимый (N-й) член найти можно, применяя следующую формулу:

К примеру: первый член (a1) в арифметической прогрессии задан и равен трём, а разность (d) равняется четырём. Найти нужно сорок пятый член этой прогрессии. a45 = 1+4(45-1)=177

Формула an = ak + d(n - k) позволяет определить n-й член арифметической прогрессии через любой ее k-тый член при условии, если он известен.

Сумма членов арифметической прогрессии (подразумевается 1-ые n членов конечной прогрессии) вычисляется следующим образом:

Sn = (a1+an) n/2.

Если известны и 1-ый член, то для вычисления удобна другая формула:

Sn = ((2a1+d(n-1))/2)*n.

Сумма арифметической прогрессии, которая содержит n членов, подсчитывается таким образом:

Выбор формул для расчетов зависит от условий задач и исходных данных.

Натуральный ряд любых чисел, таких как 1,2,3,...,n,...- простейший пример арифметической прогрессии.

Помимо арифметической прогрессии существует еще и геометрическая, которая обладает своими свойствами и характеристиками.

Если каждому натуральному числу n поставить в соответствие действительное число a n , то говорят, что задано числовую последовательность :

a 1 , a 2 , a 3 , . . . , a n , . . . .

Итак, числовая последовательность — функция натурального аргумента.

Число a 1 называют первым членом последовательности , число a 2 — вторым членом последовательности , число a 3 — третьим и так далее. Число a n называют n-м членом последовательности , а натуральное число n — его номером .

Из двух соседних членов a n и a n +1 последовательности член a n +1 называют последующим (по отношению к a n ), а a n — предыдущим (по отношению к a n +1 ).

Чтобы задать последовательность, нужно указать способ, позволяющий найти член последовательности с любым номером.

Часто последовательность задают с помощью формулы n-го члена , то есть формулы, которая позволяет определить член последовательности по его номеру.

Например,

последовательность положительных нечётных чисел можно задать формулой

a n = 2n - 1,

а последовательность чередующихся 1 и -1 — формулой

b n = (-1) n +1 . ◄

Последовательность можно определить рекуррентной формулой , то есть формулой, которая выражает любой член последовательности, начиная с некоторого, через предыдущие (один или несколько) члены.

Например,

если a 1 = 1 , а a n +1 = a n + 5

a 1 = 1,

a 2 = a 1 + 5 = 1 + 5 = 6,

a 3 = a 2 + 5 = 6 + 5 = 11,

a 4 = a 3 + 5 = 11 + 5 = 16,

a 5 = a 4 + 5 = 16 + 5 = 21.

Если а 1 = 1, а 2 = 1, a n +2 = a n + a n +1 , то первые семь членов числовой последовательности устанавливаем следующим образом:

a 1 = 1,

a 2 = 1,

a 3 = a 1 + a 2 = 1 + 1 = 2,

a 4 = a 2 + a 3 = 1 + 2 = 3,

a 5 = a 3 + a 4 = 2 + 3 = 5,

a 6 = a 4 + a 5 = 3 + 5 = 8,

a 7 = a 5 + a 6 = 5 + 8 = 13. ◄

Последовательности могут быть конечными и бесконечными .

Последовательность называется конечной , если она имеет конечное число членов. Последовательность называется бесконечной , если она имеет бесконечно много членов.

Например,

последовательность двузначных натуральных чисел:

10, 11, 12, 13, . . . , 98, 99

конечная.

Последовательность простых чисел:

2, 3, 5, 7, 11, 13, . . .

бесконечная. ◄

Последовательность называют возрастающей , если каждый её член, начиная со второго, больше чем предыдущий.

Последовательность называют убывающей , если каждый её член, начиная со второго, меньше чем предыдущий.

Например,

2, 4, 6, 8, . . . , 2n , . . . — возрастающая последовательность;

1, 1 / 2 , 1 / 3 , 1 / 4 , . . . , 1 / n , . . . — убывающая последовательность. ◄

Последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают, называется монотонной последовательностью .

Монотонными последовательностями, в частности, являются возрастающие последовательности и убывающие последовательности.

Арифметическая прогрессия

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, к которому прибавляется одно и то же число.

a 1 , a 2 , a 3 , . . . , a n , . . .

является арифметической прогрессией, если для любого натурального числа n выполняется условие:

a n +1 = a n + d ,

где d — некоторое число.

Таким образом, разность между последующим и предыдущим членами данной арифметической прогрессии всегда постоянна:

а 2 - a 1 = а 3 - a 2 = . . . = a n +1 - a n = d .

Число d называют разностью арифметической прогрессии .

Чтобы задать арифметическую прогрессию, достаточно указать её первый член и разность.

Например,

если a 1 = 3, d = 4 , то первые пять членов последовательности находим следующим образом:

a 1 =3,

a 2 = a 1 + d = 3 + 4 = 7,

a 3 = a 2 + d = 7 + 4 = 11,

a 4 = a 3 + d = 11 + 4 = 15,

a 5 = a 4 + d = 15 + 4 = 19. ◄

Для арифметической прогрессии с первым членом a 1 и разностью d её n

a n = a 1 + (n - 1)d.

Например,

найдём тридцатый член арифметической прогрессии

1, 4, 7, 10, . . .

a 1 =1, d = 3,

a 30 = a 1 + (30 - 1)d = 1 + 29· 3 = 88. ◄

a n-1 = a 1 + (n - 2)d,

a n = a 1 + (n - 1)d,

a n +1 = a 1 + nd ,

то, очевидно,

a n =	a n-1 + a n+1
	2

каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предшествующего и последующего членов.

числа a, b и c являются последовательными членами некоторой арифметической прогрессии тогда и только тогда, когда одно из них равно среднему арифметическому двух других.

Например,

a n = 2n - 7 , является арифметической прогрессией.

Воспользуемся приведённым выше утверждением. Имеем:

a n = 2n - 7,

a n-1 = 2(n - 1) - 7 = 2n - 9,

a n+1 = 2(n + 1) - 7 = 2n - 5.

Следовательно,

a n+1 + a n-1	=	2n - 5 + 2n - 9	= 2n - 7 = a n ,
2		2

◄

Отметим, что n -й член арифметической прогрессии можно найти не толь через a 1 , но и любой предыдущий a k

a n = a k + (n - k )d .

Например,

для a 5 можно записать

a 5 = a 1 + 4d ,

a 5 = a 2 + 3d ,

a 5 = a 3 + 2d ,

a 5 = a 4 + d . ◄

a n = a n-k + kd ,

a n = a n+k - kd ,

то, очевидно,

a n =	a n-k + a n+k
	2

любой член арифметической прогрессии, начиная со второго равен полусумме равноотстоящих от него членов этой арифметической прогрессии.

Кроме того, для любой арифметической прогрессии справедливо равенство:

a m + a n = a k + a l ,

m + n = k + l.

Например,

в арифметической прогрессии

1) a 10 = 28 = (25 + 31)/2 = (a 9 + a 11 )/2;

2) 28 = a 10 = a 3 + 7d = 7 + 7·3 = 7 + 21 = 28;

3) a 10 = 28 = (19 + 37)/2 = (a 7 + a 13 )/2;

4) a 2 + a 12 = a 5 + a 9 , так как

a 2 + a 12 = 4 + 34 = 38,

a 5 + a 9 = 13 + 25 = 38. ◄

S n = a 1 + a 2 + a 3 + . . . + a n ,

первых n членов арифметической прогрессии равна произведению полусуммы крайних слагаемых на число слагаемых:

Отсюда, в частности, следует, что если нужно просуммировать члены

a k , a k +1 , . . . , a n ,

то предыдущая формула сохраняет свою структуру:

Например,

в арифметической прогрессии 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, . . .

S 10 = 1 + 4 + . . . + 28 = (1 + 28) · 10/2 = 145;

10 + 13 + 16 + 19 + 22 + 25 + 28 = S 10 - S 3 = (10 + 28 ) · (10 - 4 + 1)/2 = 133. ◄

Если дана арифметическая прогрессия, то величины a 1 , a n , d , n и S n связаны двумя формулами:

Поэтому, если значения трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Арифметическая прогрессия является монотонной последовательностью. При этом:

если d > 0 , то она является возрастающей;
если d < 0 , то она является убывающей;
если d = 0 , то последовательность будет стационарной.

Геометрическая прогрессия

Геометрической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.

b 1 , b 2 , b 3 , . . . , b n , . . .

является геометрической прогрессией, если для любого натурального числа n выполняется условие:

b n +1 = b n · q ,

где q ≠ 0 — некоторое число.

Таким образом, отношение последующего члена данной геометрической прогрессии к предыдущему есть число постоянное:

b 2 / b 1 = b 3 / b 2 = . . . = b n +1 / b n = q .

Число q называют знаменателем геометрической прогрессии .

Чтобы задать геометрическую прогрессию, достаточно указать её первый член и знаменатель.

Например,

если b 1 = 1, q = -3 , то первые пять членов последовательности находим следующим образом:

b 1 = 1,

b 2 = b 1 · q = 1 · (-3) = -3,

b 3 = b 2 · q = -3 · (-3) = 9,

b 4 = b 3 · q = 9 · (-3) = -27,

b 5 = b 4 · q = -27 · (-3) = 81. ◄

b 1 и знаменателем q её n -й член может быть найден по формуле:

b n = b 1 · q n -1 .

Например,

найдём седьмой член геометрической прогрессии 1, 2, 4, . . .

b 1 = 1, q = 2,

b 7 = b 1 · q 6 = 1 · 2 6 = 64 . ◄

b n-1 = b 1 · q n -2 ,

b n = b 1 · q n -1 ,

b n +1 = b 1 · q n ,

то, очевидно,

b n 2 = b n -1 · b n +1 ,

каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому (пропорциональному) предшествующего и последующего членов.

Так как верно и обратное утверждение, то имеет место следующее утверждение:

числа a, b и c являются последовательными членами некоторой геометрической прогрессии тогда и только тогда, когда квадрат одного из них равен произведению двух других, то есть одно из чисел является средним геометрическим двух других.

Например,

докажем, что последовательность, которая задаётся формулой b n = -3 · 2 n , является геометрической прогрессией. Воспользуемся приведённым выше утверждением. Имеем:

b n = -3 · 2 n ,

b n -1 = -3 · 2 n -1 ,

b n +1 = -3 · 2 n +1 .

Следовательно,

b n 2 = (-3 · 2 n ) 2 = (-3 · 2 n -1 ) · (-3 · 2 n +1 ) = b n -1 · b n +1 ,

что и доказывает нужное утверждение. ◄

Отметим, что n -й член геометрической прогрессии можно найти не только через b 1 , но и любой предыдущий член b k , для чего достаточно воспользоваться формулой

b n = b k · q n - k .

Например,

для b 5 можно записать

b 5 = b 1 · q 4 ,

b 5 = b 2 · q 3 ,

b 5 = b 3 · q 2 ,

b 5 = b 4 · q . ◄

b n = b k · q n - k ,

b n = b n - k · q k ,

то, очевидно,

b n 2 = b n - k · b n + k

квадрат любого члена геометрической прогрессии, начиная со второго равен произведению равноотстоящих от него членов этой прогрессии.

Кроме того, для любой геометрической прогрессии справедливо равенство:

b m · b n = b k · b l ,

m + n = k + l .

Например,

в геометрической прогрессии

1) b 6 2 = 32 2 = 1024 = 16 · 64 = b 5 · b 7 ;

2) 1024 = b 11 = b 6 · q 5 = 32 · 2 5 = 1024;

3) b 6 2 = 32 2 = 1024 = 8 · 128 = b 4 · b 8 ;

4) b 2 · b 7 = b 4 · b 5 , так как

b 2 · b 7 = 2 · 64 = 128,

b 4 · b 5 = 8 · 16 = 128. ◄

S n = b 1 + b 2 + b 3 + . . . + b n

первых n членов геометрической прогрессии со знаменателем q ≠ 0 вычисляется по формуле:

А при q = 1 — по формуле

S n = nb 1

Заметим, что если нужно просуммировать члены

b k , b k +1 , . . . , b n ,

то используется формула:

S n - S k -1 = b k + b k +1 + . . . + b n = b k ·	1 - q n - k +1	.
	1 - q

Например,

в геометрической прогрессии 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, . . .

S 10 = 1 + 2 + . . . + 512 = 1 · (1 - 2 10) / (1 - 2) = 1023;

64 + 128 + 256 + 512 = S 10 - S 6 = 64 · (1 - 2 10-7+1) / (1 - 2) = 960. ◄

Если дана геометрическая прогрессия, то величины b 1 , b n , q , n и S n связаны двумя формулами:

Поэтому, если значения каких-либо трёх из этих величин даны, то соответствующие им значения двух остальных величин определяются из этих формул, объединённых в систему двух уравнений с двумя неизвестными.

Для геометрической прогрессии с первым членом b 1 и знаменателем q имеют место следующие свойства монотонности :

прогрессия является возрастающей, если выполнено одно из следующих условий:

b 1 > 0 и q > 1;

b 1 < 0 и 0 < q < 1;

прогрессия является убывающей, если выполнено одно из следующих условий:

b 1 > 0 и 0 < q < 1;

b 1 < 0 и q > 1.

Если q < 0 , то геометрическая прогрессия является знакопеременной: её члены с нечётными номерами имеют тот же знак, что и её первый член, а члены с чётными номерами — противоположный ему знак. Ясно, что знакопеременная геометрическая прогрессия не является монотонной.

Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:

P n = b 1 · b 2 · b 3 · . . . · b n = (b 1 · b n ) n / 2 .

Например,

1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 = (1 · 128) 8/2 = 128 4 = 268 435 456;

3 · 6 · 12 · 24 · 48 = (3 · 48) 5/2 = (144 1/2) 5 = 12 5 = 248 832.◄

Бесконечно убывающая геометрическая прогрессия

Бесконечно убывающей геометрической прогрессией называют бесконечную геометрическую прогрессию, модуль знаменателя которой меньше 1 , то есть

|q | < 1 .

Заметим, что бесконечно убывающая геометрическая прогрессия может не быть убывающей последовательностью. Это соответствует случаю

1 < q < 0 .

При таком знаменателе последовательность знакопеременная. Например,

1, - 1 / 2 , 1 / 4 , - 1 / 8 , . . . .

Суммой бесконечно убывающей геометрической прогрессии называют число, к которому неограниченно приближается сумма первых n членов прогрессии при неограниченном возрастании числа n . Это число всегда конечно и выражается формулой