Десятичная дробь используется, когда нужно выполнять действия с нецелыми числами. Это может показаться нерациональным. Но такой вид чисел существенно облегчает математические операции, которые с ними необходимо выполнять. Это понимание приходит со временем, когда их запись становится привычной, а прочтение не вызывает трудностей, и освоены правила десятичных дробей. Тем более что все действия повторяют уже известные, которые усвоены с натуральными числами. Только нужно запомнить некоторые особенности.

Определение десятичной дроби

Десятичная дробь — это особое представление нецелого числа со знаменателем, который делится на 10, а ответ получается в виде единицы и, возможно, нулей. Другими словами, если в знаменателе 10, 100, 1000 и так далее, то удобнее переписать число с использованием запятой. Тогда до нее будет расположена целая часть, а потом - дробная. Причем запись второй половины числа будет зависеть от знаменателя. Количество цифр, которые находятся в дробной части, должно быть равно разряду знаменателя.

Проиллюстрировать вышесказанное можно этими числами:

9/10=0,9; 178/10000=0,0178; 3,05; 56 003,7006.

Причины, по которым понадобилось применение десятичных дробей

Математикам потребовались десятичные дроби по нескольким основаниям:

    Упрощение записи. Такая дробь расположена вдоль одной линии без черточки между знаменателем и числителем, при этом наглядность не страдает.

    Простота в сравнении. Достаточно просто соотнести цифры, находящиеся в одинаковых позициях, в то время как с обыкновенными дробями пришлось бы приводить их к общему знаменателю.

    Упрощение вычислений.

    Калькуляторы не рассчитаны на введение обыкновенных дробей, они для всех операций используют десятичную запись чисел.

Как правильно прочитать такие числа?

Ответ прост: так же, как обыкновенное смешанное число со знаменателем, кратным 10. Исключение составляют только дроби без целого значения, тогда при чтении нужно произносить «ноль целых».

Например, 45/1000 нужно произнести как сорок пять тысячных , в то же время 0,045 будет звучать как ноль целых сорок пять тысячных .

Смешанное число с целой частью равной 7 и дробью 17/100, что запишется как 7,17, в обоих случаях будет прочитано как семь целых семнадцать сотых .

Роль разрядов в записи дробей

Верно отметить разряд - это то, что требует математика. Десятичные дроби и их значение могут существенно измениться, если записать цифру не в том месте. Впрочем, это было справедливо и раньше.

Для прочтения разрядов целой части десятичной дроби нужно просто воспользоваться правилами, известными для натуральных чисел. А в правой части они зеркально отражаются и по-другому читаются. Если в целой части звучало "десятки", то после запятой это будут уже "десятые".

Наглядно это можно увидеть в этой таблице.

Таблица разрядов десятичной дроби
класс тысячи единицы , дробная часть
разряд сот. дес. ед. сот. дес. ед. десятая сотая тысячная десятитысячная

Как правильно записать смешанное число десятичной дробью?

Если в знаменателе стоит число, равное 10 или 100, и прочие, то вопрос о том, как дробь перевести в десятичную, несложен. Для этого достаточно по-другому переписать все ее составные части. В этом помогут такие пункты:

    немного в стороне написать числитель дроби, в этот момент десятичная запятая располагается справа, после последней цифры;

    переместить запятую влево, здесь самое главное - правильно сосчитать цифры — передвинуть ее нужно на столько позиций, сколько нолей в знаменателе;

    если их не хватает, то на пустых позициях должны оказаться нули;

    нули, которые были в конце числителя, теперь не нужны, и их можно зачеркнуть;

    перед запятой приписать целую часть, если ее не было, то здесь тоже окажется нуль.

Внимание. Нельзя зачеркивать нули, которые оказались окружены другими цифрами.

О том, как быть в ситуации, когда в знаменателе число не только из единицы и нулей, как дробь переводить в десятичную, можно прочитать чуть ниже. Это важная информация, с которой обязательно стоит ознакомиться.

Как дробь перевести в десятичную, если знаменатель - произвольное число?

Здесь возможны два варианта:

    Когда знаменатель можно представить в виде числа, которое равно десяти в любой степени.

    Если такую операцию проделать нельзя.

Как это проверить? Нужно разложить знаменатель на множители. Если в произведении присутствуют только 2 и 5, то все хорошо, и дробь легко преобразуется в конечную десятичную. В противном случае, если появляются 3, 7 и другие простые числа, то результат будет бесконечным. Такую десятичную дробь для удобства использования в математических операциях принято округлять. Об этом будет речь немного ниже.

Изучает, как получаются такие десятичные дроби, 5 класс. Примеры здесь будут очень кстати.

Пусть в знаменателях находятся числа: 40, 24 и 75. Разложение на простые множители для них будет такое:

  • 40=2·2·2·5;
  • 24=2·2·2·3;
  • 75=5·5·3.

В этих примерах только первая дробь может быть представлена в виде конечной.

Алгоритм перевода обыкновенной дроби в конечную десятичную

    Проверить разложение знаменателя на простые множители и убедиться в том, что оно будет состоять из 2 и 5.

    Добавить к этим числам столько 2 и 5, чтобы их стало равное количество. Они дадут значение дополнительного множителя.

    Произвести умножение знаменателя и числителя на это число. В результате получится обыкновенная дробь, под чертой у которой стоит 10 в некоторой степени.

Если в задаче эти действия выполняются со смешанным числом, то его сначала нужно представить в виде неправильной дроби. А уже потом действовать по описанному сценарию.

Представление обыкновенной дроби в виде округленной десятичной

Этот способ того, как дробь переводить в десятичную, кому-то покажется даже проще. Потому что в нем нет большого количества действий. Нужно только разделить значение числителя на знаменатель.

К любому числу с десятичной частью справа от запятой можно приписать бесконечное количество нулей. Этим свойством и нужно воспользоваться.

Сначала записать целую часть и поставить после нее запятую. Если дробь правильная, то написать ноль.

Потом полагается выполнить деление числителя на знаменатель. Так, чтобы количество цифр у них было одинаковым. То есть приписать справа у числителя нужное количество нолей.

Выполнять деление в столбик до тех пор, пока не будет набрано нужное количество цифр. Например, если округлить нужно будет до сотых, то в ответе их должно быть 3. В общем, цифр должно быть на одну больше, чем нужно получить в итоге.

Записать промежуточный ответ после запятой и округлить по правилам. Если последняя цифра - от 0 до 4, то ее нужно просто отбросить. А когда она равна 5-9, то стоящую перед ней нужно увеличить на единицу, отбросив последнюю.

Возврат от десятичной дроби к обыкновенной

В математике встречаются задачи, когда десятичные дроби удобнее представить в виде обыкновенных, в которых есть числитель со знаменателем. Можно вздохнуть с облегчением: эта операция возможна всегда.

Для этой процедуры нужно сделать следующее:

    записать целую часть, если она равна нулю, то ничего писать не надо;

    провести дробную черту;

    над ней записать цифры из правой части, если первыми идут нули, то их нужно зачеркнуть;

    под чертой написать единицу с таким количеством нолей, сколько цифр стоит после запятой в первоначальной дроби.

    Это все, что нужно сделать, чтобы перевести десятичную дробь в обыкновенную.

    Что можно делать с десятичными дробями?

    В математике это будут определенные действия с десятичными дробями, которые ранее выполнялись для других чисел.

    Ими являются:

      сравнение;

      сложение и вычитание;

      умножение и деление.

    Первое действие, сравнение, похоже на то, как это делалось для натуральных чисел. Чтобы определить, какое больше, нужно сравнивать разряды целой части. Если они окажутся равными, то переходят к дробной и так же по разрядам сравнивают их. То число, где окажется большая цифра в старшем разряде, и будет ответом.

    Сложение и вычитание десятичных дробей

    Это, пожалуй, самые простые действия. Потому что выполняются по правилам для натуральных чисел.

    Так, чтобы выполнить сложение десятичных дробей, их нужно записать друг под другом, разместив запятые в столбик. При такой записи слева от запятых оказываются целые части, а справа — дробные. И теперь нужно сложить цифры поразрядно, как это делается с натуральными числами, снеся вниз запятую. Начинать сложение нужно с самого маленького разряда дробной части числа. Если в правой половине не хватает цифр, то дописывают нули.

    При вычитании действуют так же. И здесь действует правило, которое описывает возможность занять единицу у старшего разряда. Если в уменьшаемой дроби после запятой меньше цифр, чем у вычитаемого, то в ней просто приписывают нули.

    Немного сложнее обстоит дело с заданиями, где нужно выполнить умножение и деление десятичных дробей.

    Как умножить десятичную дробь в разных примерах?

    Правило, по которому производится умножение десятичных дробей на натуральное число, такое:

      записать их в столбик, не обращая внимания на запятую;

      перемножить, как если бы они были натуральными;

      отделить запятой столько цифр, сколько их было в дробной части исходного числа.

    Частным случаем является пример, в котором натуральное число равно 10 в любой степени. Тогда для получения ответа нужно просто передвинуть запятую вправо на столько позиций, сколько нулей в другом множителе. Иными словами, при умножении на 10 запятая сдвигается на одну цифру, на 100 - их будет уже две, и так далее. Если цифр в дробной части не хватает, то нужно записать на пустых позициях нули.

    Правило, которым пользуются, когда в задании нужно произвести умножение десятичных дробей на другое такое же число:

      записать их друг под другом, не обращая внимания на запятые;

      умножить, как если бы они были натуральными;

      отделить запятой столько цифр, сколько их было в дробных частях обеих исходных дробях вместе.

    Частным случаем выделяются примеры, в которых один из множителей равен 0,1 или 0,01 и далее. В них нужно выполнить перемещение запятой влево на количество цифр в представленных множителях. То есть если умножается на 0,1, то запятая сдвигается на одну позицию.

    Как разделить десятичную дробь в разных заданиях?

    Деление десятичных дробей на натуральное число выполняется по такому правилу:

      записать их для деления в столбик, как если бы они были натуральными;

      делить по привычному правилу до тех пор, пока не закончится целая часть;

      поставить в ответ запятую;

      продолжить деление дробной составляющей до получения в остатке нуля;

      если нужно, то можно приписать нужное количество нулей.

    Если целая часть равна нулю, то и в ответе ее тоже не будет.

    Отдельно стоит деление на числа, равные десятке, сотне и так далее. В таких задачах нужно передвинуть запятую влево на количество нулей в делителе. Бывает, что цифр в целой части не хватает, тогда вместо них используют нули. Можно заметить, что эта операция подобна умножению на 0,1 и подобным ей числам.

    Чтобы выполнить деление десятичных дробей, нужно воспользоваться этим правилом:

      превратить делитель в натуральное число, а для этого перенести в нем запятую вправо до конца;

      выполнить перемещение запятой и в делимом на такое же число цифр;

      действовать по предыдущему сценарию.

    Выделяется деление на 0,1; 0,01 и прочие подобные числа. В таких примерах запятая сдвигается вправо на число цифр в дробной части. Если они закончились, то нужно приписать недостающее количество нулей. Стоит отметить, что это действие повторяет деление на 10 и подобные ему числа.

    Заключение: все дело в практике

    Ничто в учебе не дается легко и без усилий. Для надежного освоения нового материала требуются время и тренировка. Математика не исключение.

    Чтобы тема про десятичные дроби не вызывала затруднений, нужно решать с ними примеров как можно больше. Ведь было время, когда и сложение натуральных чисел ставило в тупик. А теперь все нормально.

    Поэтому, перефразируя известную фразу: решать, решать и еще раз решать. Тогда и задания с такими числами будут выполняться легко и непринужденно, как очередная головоломка.

    Кстати, и головоломки поначалу решаются сложно, а потом нужно делать привычные движения. Так же и в математических примерах: пройдя по одному пути несколько раз, потом уже не будешь задумываться над тем, куда повернуть.

Данный материал мы посвятим такой важной теме, как десятичные дроби. Сначала определимся с основными определениями, приведем примеры и остановимся на правилах десятичной записи, а также на том, что из себя представляют разряды десятичных дробей. Далее выделим основные виды: конечные и бесконечные, периодические и непериодические дроби. В финальной части мы покажем, как точки, соответствующие дробным числам, расположены на оси координат.

Yandex.RTB R-A-339285-1

Что такое десятичная запись дробных чисел

Так называемая десятичная запись дробных чисел может быть использована как для натуральных, так и для дробных чисел. Она выглядит как набор из двух и более цифр, между которыми есть запятая.

Десятичная запятая нужна для того, чтобы отделять целую часть от дробной. Как правило, последняя цифра десятичной дроби не бывает нулем, за исключением случаев, когда десятичная запятая стоит сразу после первого же нуля.

Какие можно привести примеры дробных чисел в десятичной записи? Это может быть 34 , 21 , 0 , 35035044 , 0 , 0001 , 11 231 552 , 9 и др.

В некоторых учебниках можно встретить использование точки вместо запятой (5 . 67 , 6789 . 1011 и др.) Это вариант считается равнозначным, но он более характерен для англоязычных источников.

Определение десятичных дробей

Основываясь на указанном выше понятии десятичной записи, мы можем сформулировать следующее определение десятичных дробей:

Определение 1

Десятичные дроби представляют собой дробные числа в десятичной записи.

Для чего нам нужна запись дробей в такой форме? Она дает нам некоторые преимущества перед обыкновенными, например, более компактную запись, особенно в тех случаях, когда в знаменателе стоят 1000 , 100 , 10 и др. или смешанное число. Например, вместо 6 10 мы можем указать 0 , 6 , вместо 25 10000 – 0 , 0023 , вместо 512 3 100 – 512 , 03 .

О том, как правильно представить в десятичном виде обыкновенные дроби с десятками, сотнями, тысячами в знаменателе, будет рассказано в рамках отдельного материала.

Как правильно читать десятичные дроби

Существуют некоторые правила чтения записей десятичных дробей. Так, те десятичные дроби, которым соответствуют их правильные обыкновенные эквиваленты, читаются почти так же, но с добавлением слов «ноль десятых» в начале. Так, запись 0 , 14 , которой соответствует 14 100 , читается как «ноль целых четырнадцать сотых».

Если же десятичной дроби можно поставить в соответствие смешанное число, то она читается тем же образом, как и это число. Так, если у нас есть дробь 56 , 002 , которой соответствует 56 2 1000 , мы читаем такую запись как «пятьдесят шесть целых две тысячных».

Значение цифры в записи десятичной дроби зависит от того, на каком месте она расположена (так же, как и в случае с натуральными числами). Так, в десятичной дроби 0 , 7 семерка – это десятые доли, в 0 , 0007 – десятитысячные, а в дроби 70 000 , 345 она означает семь десятков тысяч целых единиц. Таким образом, в десятичных дробях тоже существует понятие разряда числа.

Названия разрядов, расположенных до запятой, аналогичны тем, что существуют в натуральных числах. Названия тех, что расположены после, наглядно представлены в таблице:

Разберем пример.

Пример 1

У нас есть десятичная дробь 43 , 098 . У нее в разряде десятков находится четверка, в разряде единиц тройка, в разряде десятых – ноль, сотых – 9 , тысячных – 8 .

Принято различать разряды десятичных дробей по старшинству. Если мы движемся по цифрам слева направо, то мы будем идти от старших разрядов к младшим. Получается, что сотни старше десятков, а миллионные доли младше, чем сотые. Если взять ту конечную десятичную дробь, которую мы приводили в качестве примера выше, то в ней старшим, или высшим будет разряд сотен, а младшим, или низшим – разряд 10 -тысячных.

Любую десятичную дробь можно разложить по отдельным разрядам, то есть представить в виде суммы. Это действие выполняется так же, как и для натуральных чисел.

Пример 2

Попробуем разложить дробь 56 , 0455 по разрядам.

У нас получится:

56 , 0455 = 50 + 6 + 0 , 4 + 0 , 005 + 0 , 0005

Если мы вспомним свойства сложения, то сможем представить эту дробь и в других видах, например, как сумму 56 + 0 , 0455 , или 56 , 0055 + 0 , 4 и др.

Что такое конечные десятичные дроби

Все дроби, о которых мы говорили выше, являются конечными десятичными дробями. Это означает, что количество цифр, расположенное у них после запятой, является конечным. Выведем определение:

Определение 1

Конечные десятичные дроби представляют собой вид десятичных дробей, у которых после знака запятой стоит конечное число знаков.

Примерами таких дробей могут быть 0 , 367 , 3 , 7 , 55 , 102567958 , 231 032 , 49 и др.

Любую из этих дробей можно перевести либо в смешанное число (если значение их дробной части отличается от нуля), либо в обыкновенную дробь (при нулевой целой части). Тому, как это делается, мы посвятили отдельный материал. Здесь просто укажем пару примеров: так, конечную десятичную дробь 5 , 63 мы можем привести к виду 5 63 100 , а 0 , 2 соответствует 2 10 (или любая другая равная ей дробь, например, 4 20 или 1 5 .)

Но обратный процесс, т.е. запись обыкновенной дроби в десятичном виде, может быть выполнен не всегда. Так, 5 13 нельзя заменить на равную дробь с знаменателем 100 , 10 и др., значит, конечная десятичная дробь из нее не получится.

Основные виды бесконечных десятичных дробей: периодические и непериодические дроби

Мы указывали выше, что конечные дроби называются так потому, что после запятой у них стоит конечное число цифр. Однако оно вполне может быть и бесконечным, и в этом случае сами дроби также будут называться бесконечными.

Определение 2

Бесконечными десятичными дробями называются такие, у которых после запятой стоит бесконечное количество цифр.

Очевидно, что полностью такие числа записаны быть просто не могут, поэтому мы указываем лишь часть из них и дальше ставим многоточие. Это знак говорит о бесконечном продолжении последовательности знаков после запятой. Примерами бесконечных десятичных дробей могут быть 0 , 143346732 … , 3 , 1415989032 … , 153 , 0245005 … , 2 , 66666666666 … , 69 , 748768152 … . и т.д.

В «хвосте» такой дроби могут стоять не только случайные на первый взгляд последовательности цифр, но постоянное повторение одного и того же знака или группы знаков. Дроби с чередованием после десятичной запятой называются периодическими.

Определение 3

Периодическими десятичными дробями называются такие бесконечные десятичные дроби, у которых после запятой повторяется одна цифра или группа из нескольких цифр. Повторяющаяся часть называется периодом дроби.

К примеру, для дроби 3 , 444444 … . периодом будет цифра 4 , а для 76 , 134134134134 … – группа 134 .

Какое же минимальное количество знаков допустимо оставить в записи периодической дроби? Для периодических дробей достаточно будет записать весь период один раз в круглых скобках. Так, дробь 3 , 444444 … . правильно будет записать как 3 , (4) , а 76 , 134134134134 … – как 76 , (134) .

В целом записи с несколькими периодами в скобках будут иметь точно такой же смысл: к примеру, периодическая дробь 0 , 677777 – это то же самое, что 0 , 6 (7) и 0 , 6 (77) и т.д. Также допустимы записи вида 0 , 67777 (7) , 0 , 67 (7777) и др.

Во избежание ошибок введем однообразие обозначений. Условимся записывать только один период (максимально короткую последовательность цифр), который стоит ближе всего к десятичной запятой, и заключать его в круглые скобки.

То есть для указанной выше дроби основной будем считать запись 0 , 6 (7) , а, например, в случае с дробью 8 , 9134343434 будем писать 8 , 91 (34) .

Если знаменатель обыкновенной дроби содержит простые множители, не равные 5 и 2 , то при переводе в десятичную запись из них получатся бесконечные дроби.

В принципе, любую конечную дробь мы можем записать в виде периодической. Для этого нам просто нужно добавить справа бесконечно много нулей. Как это выглядит в записи? Допустим, у нас есть конечная дробь 45 , 32 . В периодическом виде она будет выглядеть как 45 , 32 (0) . Это действие возможно потому, что добавление нулей справа в любую десятичную дробь дает нам в результате равную ей дробь.

Отдельно следует остановиться на периодических дробях с периодом 9 , например, 4 , 89 (9) , 31 , 6 (9) . Они являются альтернативной записью схожих дробей с периодом 0 , поэтому их часто заменяют при письме именно дробями с нулевым периодом. При этом к значению следующего разряда добавляют единицу, а в круглых скобках указывают (0) . Равенство получившихся чисел легко проверить, представив их в виде обыкновенных дробей.

К примеру, дробь 8 , 31 (9) можно заменить на соответствующую ей дробь 8 , 32 (0) . Или 4 , (9) = 5 , (0) = 5 .

Бесконечные десятичные периодические дроби относятся к рациональным числам. Иначе говоря, любую периодическую дробь можно представить в виде обыкновенной, и наоборот.

Существуют и дроби, у которых после запятой бесконечно повторяющаяся последовательность отсутствует. В таком случае их называют непериодическими дробями.

Определение 4

К непериодическим десятичным дробям относятся те бесконечные десятичные дроби, в которых после запятой не содержится периода, т.е. повторяющейся группы цифр.

Иногда непериодические дроби выглядят очень похожими на периодические. Например, 9 , 03003000300003 … на первый взгляд кажется имеющей период, однако подробный анализ знаков после запятой подтверждает, что это все же непериодическая дробь. С такими числами надо быть очень внимательным.

Непериодические дроби относятся к иррациональным числам. В обыкновенные дроби их не переводят.

Основные действия с десятичными дробями

С десятичными дробями можно производить следующие действия: сравнение, вычитание, сложение, деление и умножение. Разберем каждое из них отдельно.

Сравнение десятичных дробей может быть сведено к сравнению обыкновенных дробей, которые соответствуют исходным десятичным. Но бесконечные непериодические дроби свести к такому виду нельзя, а перевод десятичных дробей в обыкновенные зачастую является трудоемкой задачей. Как же быстро произвести действие сравнения, если нам нужно сделать это по ходу решения задачи? Удобно сравнивать десятичные дроби по разрядам таким же образом, как мы сравниваем натуральные числа. Этому методу мы посвятим отдельную статью.

Чтобы складывать одни десятичные дроби с другими, удобно использовать метод сложения столбиком, как для натуральных чисел. Чтобы складывать периодические десятичные дроби, необходимо предварительно заменить их обыкновенными и считать по стандартной схеме. Если же по условиям задачи нам надо сложить бесконечные непериодические дроби, то нужно перед этим округлить их до некоторого разряда, а потом уже складывать. Чем меньше разряд, до которого мы округляем, тем выше будет точность вычисления. Для вычитания, умножения и деления бесконечных дробей предварительное округление также необходимо.

Нахождение разности десятичных дробей обратно действию сложения. По сути, с помощью вычитания мы можем найти такое число, сумма которого с вычитаемой дробью даст нам уменьшаемую. Подробнее об этом расскажем в рамках отдельного материала.

Умножение десятичных дробей производится так же, как и для натуральных чисел. Для этого тоже подходит метод вычисления столбиком. Это действие с периодическими дробями мы опять же сводим к умножению обыкновенных дробей по уже изученным правилам. Бесконечные дроби, как мы помним, надо округлить перед подсчетами.

Процесс деления десятичных дробей является обратным процессу умножения. При решении задач мы также пользуемся подсчетами в столбик.

Можно установить точное соответствие между конечной десятичной дробью и точкой на оси координат. Выясним, как отметить точку на оси, которая будет точно соответствовать необходимой десятичной дроби.

Мы уже изучали, как построить точки, соответствующие обыкновенным дробям, а ведь десятичные дроби можно привести к такому виду. Например, обыкновенная дробь 14 10 – это то же самое, что и 1 , 4 , поэтому соответствующая ей точка будет удалена от начала отсчета в положительном направлении ровно на такое же расстояние:

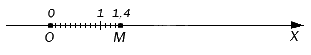
Можно обойтись без замены десятичной дроби на обыкновенную, а взять на основу метод разложения по разрядам. Так, если нам надо отметить точку, координата которой будет равна 15 , 4008 , то мы предварительно представим это число в виде суммы 15 + 0 , 4 + , 0008 . Для начала отложим от начала отсчета 15 целых единичных отрезков в положительном направлении, потом 4 десятых доли одного отрезка, а потом 8 десятитысячных долей одного отрезка. В итоге мы получим точку координат, которой соответствует дробь 15 , 4008 .

Для бесконечной десятичной дроби лучше пользоваться именно этим способом, поскольку он позволяет приблизиться к нужной точке сколь угодно близко. В некоторых случаях можно построить и точное соответствие бесконечной дроби на оси координат: так, 2 = 1 , 41421 . . . , и с этой дробью может быть соотнесена точка на координатном луче, удаленная от 0 на длину диагонали квадрата, сторона которого будет равна одному единичному отрезку.

Если мы находим не точку на оси, а десятичную дробь, соответствующую ей, то это действие называется десятичным измерением отрезка. Посмотрим, как правильно это сделать.

Допустим, нам нужно попасть от нуля в заданную точку на оси координат (или максимально приблизиться в случае с бесконечной дробью). Для этого мы постепенно откладываем единичные отрезки от начала координат, пока не попадем в нужную точку. После целых отрезков при необходимости отмеряем десятые, сотые и более мелкие доли, чтобы соответствие было максимально точным. В итоге мы получили десятичную дробь, которая соответствует заданной точке на оси координат.

Выше мы приводили рисунок с точкой M . Посмотрите на него еще раз: чтобы попасть в эту точку, нужно отмерить от нуля один единичный отрезок и четыре десятых доли от его, поскольку этой точке соответствует десятичная дробь 1 , 4 .

Если мы не можем попасть в точку в процессе десятичного измерения, то значит, что ей соответствует бесконечная десятичная дробь.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 242. Числовые поля

Понятие числа прошло длинный путь исторического развития. В главе II (см. ч. I) мы рассказали о том, как от простейших, натуральных чисел человек пришел к более сложным, действительным числам. Сейчас мы хотим вернуться к рассмотрению этого вопроса. Но при этом нам придется несколько отступить от того порядка, в котором исторически развивалось понятие числа.

Одним из простейших числовых множеств является множество натуральных чисел

В нем всегда выполнимы два основных алгебраических действия: сложение и умножение. Это означает, что, каковы бы ни были натуральные числа m и n , сумма их m + n , а также произведение m n являются непременно натуральными числами. При этом соблюдаются следующие пять законов:

1) коммутативный закон сложения:

m + n = n + m

2) ассоциативный закон сложения:

(m + n) + k = m + (n + k)

3) коммутативный закон умножения:

m n = n m

4) ассоциативный закон умножения:

(m n) k = m (n k) ;

5) дистрибутивный закон умножения относительно сложения:

(m + n) k = m k + n k .

Что касается вычитания и деления, то эти два действия в множестве натуральных чисел выполнимы не всегда. Так, ни одна из разностей 3-5 и 2-2, а также, ни одно из частных 3: 5 и 7: 4 нельзя выразить никаким натуральным числом.

Чтобы действие вычитания было выполнимым всегда, множество натуральных чисел нужно расширить путем присоединения к нему всех отрицательных целых чисел и нуля. В результате такого расширения мы приходим к множеству всех целых чисел:

3,-2,-1,0, 1,2,3.....

Числовое множество, в котором всегда выполнимы сложение и умножение, подчиненные указанным выше пяти законам, а также вычитание, называется кольцом. Таким образом, множество всех целых чисел образует кольцо .

Расширив множество всех натуральных чисел до множества всех целых чисел, мы добились тем самым, что действие вычитания стало выполнимым всегда. Но деление по-прежнему осталось, вообще говоря, невыполнимым. Чтобы устранить этот пробел, нужно расширить и множество всех целых чисел. Сделать это можно путем присоединения к нему всех обыкновенных дробей, то есть чисел вида m / n , где т и п - произвольные целые числа и п =/= 0. В результате такого расширения мы получаем множество всех рациональных чисел . Как было показано во второй главе, в этом числовом множестве всегда выполнимы действия сложения, умножения, вычитания и деления (кроме деления на нуль), причем первые два из них подчинены пяти основным законам сложения и умножения.

Множество чисел, в котором всегда выполнимы действия сложения и умножения, подчиненные пяти основным законам, а также действия вычитания и деления (кроме деления на нуль), называется полем. Множество всех рациональных чисел является простейшим числовым полем .

Уместно сразу же заметить, что множество всех иррациональных чисел поля не образует. Действительно, любое из четырех действий (сложение, умножение, вычитание и деление) над иррациональными числами может привести к числу рациональному. Так, например,

√2 + (- √2 ) = 0,

√2 √2 = 2

и т. д. А вот множество всех действительных чисел образует поле. Как указывалось во второй главе, действия сложения, умножения, вычитания и деления действительных чисел (кроме деления на нуль) не выводят нас за пределы действительных чисел, причем сложение и умножение подчинены пяти основным законам.

Приведем еще один, более сложный, пример числового поля. Рассмотрим все действительные числа вида r + s √2 , где r и s - рациональные числа.

Пусть а + b √2 и с + d √2 - произвольные два числа рассматриваемого вида. Тогда

(а + b √2 ) + (с + d √2 ) = (a + с ) + (b + d )√2

(а + b √2 ) - (с + d √2 ) = (a - с ) + (b - d )√2

(а + b √2 ) (с + d √2 ) = ac + ad √2 + bc √2 + 2 bd = (ac + 2bd ) + (ad + bc )√2 .

Предположим теперь, что число с + d √2 не равно нулю. Тогда, очевидно, и сопряженное ему число с - d √2 будет отлично от нуля (докажите это!). Поэтому можно написать:

Как мы видим, каждое из четырех действий (сложение, вычитание, умножение и деление) над числами вида r + s √2 приводит к числу того же самого вида. Ясно также, что сложение и умножение всех этих чисел подчинено каждому из пяти указанных выше законов. Поэтому совокупность всех чисел вида r + s √2 , где и r и s - рациональные числа, образует числовое поле.

Упражнения

1967. Образует ли кольцо:

а) множество всех четных чисел;

б) множество всех нечетных чисел;

в) множество всех чисел, кратных некоторому числу р ?

1968. Образует ли поле:

а) множество всех дробей со знаменателем 3;

б) множество всех дробей, знаменатели которых есть целые степени числа 3?

1969. Докажите, что множество всех конечных десятичных дробей образует кольцо, но не образует поле.

1970. Докажите, что любое числовое поле либо совпадает с множеством всех рациональных чисел, либо содержит в себе это множество.

1971. Докажите, что множество всех чисел вида а + b √3 , где а и b - рациональные числа, является полем. Содержит ли это поле:

а) все рациональные числа;

б) все иррациональные числа;

в) все действительные числа?

1967. а) Да; б) нет; в) да. 1968. а) Нет; б) нет.

Понятие равномощности множеств и его свойства позволяют выделить классы равномощных множеств. Интересно знать, как много существует неравномощных множеств и иметь в некотором смысле «эталонные множества», чтобы, сравнивая с ними другие, было легче устанавливать равномощность множеств или её отсутствие.

1. Конечных, но не равномощных множеств, бесконечно много. Их классов столько же, сколько натуральных чисел.

2. Бесконечных, но не равномощных множеств, также бесконечно много.

Возникает вопрос: есть ли среди бесконечных множеств множество наименьшей мощности? Да. Это счётные множества.

Определение 1. ПустьN - множество натуральных чисел. МножествоS называетсясчётным множеством, если оно равномощноN , то естьS N .

Мощность счётного множества имеет специальное обозначение: (первая буква алфавита иврит, читается «алеф-нуль»). Мы будем обозначать мощность счётного множества буквойа :

Примеры счётных множеств

1. 2 N ;

2. Q ;

3. Z ;

4. Множество квадратов натуральных чисел.

Основные свойства счётных множеств

Теорема 1. Для того чтобы множествоS было счётным необходимо и достаточно, чтобы его элементы можно было занумеровать в последовательность, члены которой попарно различны:

.

Доказательство:

1. Необходимость.

Пусть S - счётное множество, тогда существует биекцияf : N S . В этой биекции образ элементаn обозначима n , тем самым будут занумерованы все элементы множестваS , то есть
. Так как все элементы множестваS различны, то и все члены последовательности
попарно различны.

2. Достаточность.

Пусть
,а n попарно различны. Сопоставим элементуа n его номерn . Полученное соответствие изS вN является биекцией. Следовательно, по определениюS - счётное множество.

Теорема 2. Во всяком бесконечном множествеА имеется счётное подмножество.

Доказательство:

Возьмём во множестве А произвольный элемент. Множество
бесконечное (доказывается от противного). Из множества
выберем элемент. Множество
- бесконечное. Из множества
выбираем элементи так далее. Так какА – бесконечное множество, то этот процесс продолжим до бесконечности. В результате получим последовательность
. Так как во множествеА все элементы попарно различны, по теореме 1S - счётное множество.

Следствие. Счётная мощность является наименьшей из мощностей бесконечных множеств.

Доказательство:

Пусть А - произвольное бесконечное множество. По теореме 2 оно содержит счётное подмножествоS , то естьm (S )=а . Так какS  , тоm (S ) m (А) илиа m (А) .

Теорема3. Всякое бесконечное подмножествоВ счётного множестваS счётно:

В S ; m (S )=а m (В)=а.

Доказательство:

Так как В S , тоm (В) m (S )=а . Но по следствиюm (В) а. Таким образом,m (В) а иm (В) а. По теореме Кантора-Бернштейнаm (В)=а .

Теорема 4. Бесконечное множествоВ счётно, если существует сюрьекцияf какого-нибудь счётного множестваS наВ .

Доказательство:

Не умоляя общности доказательства можно считать, что S = N . По условиюf : N  - сюрьекция (В – это образN при отображенииf , то естьf (N )=В ). Возьмём любой элемент
,b – образ какого-либо натурального числа. При отображенииf его прообразом является некоторое множество натуральных чиселf -1 (b ) , состоящее из тех элементов, образ которых равенb , то естьf -1 (в)={ n N : f (n )= b } . В этом множестве существует наименьшее натуральное число. Рассмотрим множество
- бесконечное множество (От противного: пустьА конечно. Тогда для бесконечного числа элементов
существует один элемент
N , то есть одному элементуn N соответствует бесконечно много элементов
. Это означает, что соответствиеN  не является отображением. Получили противоречие с условием. Следовательно, предположение не верно.). Так какА N иА – бесконечное множество, то по теореме 3 множествоА счётно. Рассмотрим соответствие
, при котором
. Это соответствие является биекцией. Следовательно,А В иВ счётно.

Определение 2. Кортежем называется конечное множество элементов.

Теорема 5. МножествоК всевозможных кортежей, составленных из натуральных чисел, счётно.

Доказательство:

Пусть Р - множество всех простых чисел, расположенных в порядке возрастания:

Р=(р к ), р 1 =2, р 2 =3, р 3 =5,… .

Возьмём любой кортеж из натуральных чисел (n 1 , n 2 ,…, n k ) и поставим в соответствие ему число

N .

Например,

На основании теоремы о единственности разложения чисел на простые множители различным кортежам соответствуют различные натуральные числа, то есть если

То

.

Рассмотрим соответствие f : K А , гдеА – некоторое бесконечное подмножество множестваN , то естьА - счётно (по теореме 3). Указанное соответствие является биекцией. Так какА счётно и , тоK также счётно.

Определение 3. Декартовым произведением А 1 А 2 … А m называется множество, состоящее из кортежей
, где.

Теорема 6. Декартово произведение конечного числа счётных множеств счётно.

Доказательство:

Пусть А 1 ,А 2 ,…,А m А 1 А 2 … А m =А - счётное множество. Счётные множестваА k ,
,

…………………………………

Возьмём , поставим ему в соответствие кортеж из натуральных чисел
. Обозначим
. Указанное соответствие является биекциейf :А  1 . Но 1 – бесконечное подмножество счётного множестваиз теоремы 5. По теореме 3 1 счётно. Так какf - биекция, тоА счётно.

Теорема 7. Объединение конечной или счётной совокупности счётных множеств счётно.

Доказательство:

Пусть А 1 ,А 2 ,…,А m ,… - счётные множества. Докажем, что
- счётное множество.

1. Пусть
- объединение счётного числа счётных множеств. Счётные множестваА m представим в виде последовательностей

…………………………………

……………………………………

,

где
- это элемент множествас номером. Рассмотрим множествоN 2 = N ´N . Оно счётно по теореме 6. Возьмём любой элемент(p , q ) Î N 2 . Сопоставим ему элемент
. Так как любой элемент
принадлежит хотя бы одному из множествА p и имеет в нём определённый номерq , то указанное соответствие является сюрьекциейf : N 2 ®A . Так как множествоN 2 счётно, то по теореме 4 множествоА счётно.

2. Пусть
- объединение конечного числа счётных множеств. Положим

,

тогда
. По первой части теоремы множествоА счётно.

Теорема 8. МножествоQ рациональных чисел счётно.

Доказательство:

Представим множество Q в виде

Q = Q +
Q - ,

Q + ={m/n, m,n N , (m,n)=1},

={m/n, m,n },

Q +
,

,

где Q n - множество дробей видас фиксируемым знаменателем. Очевидно, чтоQ n , то естьQ n счётное множество. Тогда по теореме 7 также счётно. НоQ + является бесконечным подмножеством счётного множества . Тогда по теореме 3 множествоQ + счётно. В силу того, чтоQ + ~ Q - , заключаем, что множествоQ - счётно. По теореме 7 множествоQ + Q - счётно, тогда по теореме 1 множествоQ счётно.

Теорема 9. Объединение счётной совокупности конечных множеств конечно или счётно.

Доказательство:

Пусть
- конечные множества,
.

1. Множество А может быть конечным (например, если все множестваА k равны:
N ).

2. Рассмотрим случай, когда множество А - бесконечно. Пусть множествоА k имеетn k элементов. Присоединим к этому множеству все натуральные числа, большие чемn k , получим счётное множествоВ k . Проделаем это для всехk . Рассмотрим множество
. По теореме 7 множествоВ счётно. НоА  и является его бесконечным подмножеством. По теореме 3 множествоА счётно.

Теорема 10. Мощность бесконечного множества не изменяется, если к нему присоединить конечное или счётное множествоS .

Доказательство:

Случай конечного множества S не интересен, так как является следствием теоремы 1. Рассмотрим случай счётного множестваS . Не нарушая общности доказательства будем считать, что
=. По теореме 2 множествоВ можно представить в виде
, гдеS 1 - счётное множество множестваS . Тогда

Так как множества
иS 1 - счётные множества, то существует биекцияf :
S 1 . Рассмотрим отображение, определяемое следующим образом:

Это отображение является биекцией
. Следовательно,
, то есть
.

Определение 4. Если бесконечное множество не является счётным, то оно называетсянесчётным.

Теорема 11. Мощность несчётного множестваМ не изменяется, если из него удалить конечное или счётное подмножествоS .

Доказательство:

Пусть М – несчётное множество, тогдаМ \S – бесконечное множество (доказательство от противного). Тогда по теореме 10 .

Определение 5. Числоназываетсяалгебраическим, если оно является корнем некоторого многочлена с целыми коэффициентами.

Теорема 12. МножествоА всех алгебраических чисел счётно.

Доказательство:

Пусть М – множество всех многочленов с целыми коэффициентами,М n – множество многочленов с целыми коэффициентами и с фиксированной степеньюn . Возьмём любой многочлен
,
, из множестваМ n . Этому многочлену сопоставим кортеж из его коэффициентов(а n ,…,а 0 ) . Множество таких кортежей обозначимТ . Очевидно, чтоТ=(Z \{0}) Z n . Построенное соответствие является биекциейf : М n T . Так как множествоZ счётно, то по теореме 3 множествоZ \{0} также счётно. Следовательно, по теореме 6 множествоТ счётно. Так какf – биекция, тоМ n ~ T , то естьМ n счётно. Так как
и все множестваМ n счётны, то по теореме 7 множествоМ счётно. Итак, множество всех многочленов с целыми коэффициентами счётно и любой многочлен имеет конечное число корней. Следовательно, множествоА представляет собой объединение счётного числа конечных множеств. Так какА – бесконечное множество, то по теореме 9 оно счётно.

объединение равномощно .

Выделим в счетное подмножество ; остаток обозначим через . Тогда нам надо доказать, что равномощно (знак символизирует объединение непересекающихся множеств). Поскольку и оба счетны, между ними существует взаимно однозначное соответствие. Его легко продолжить до соответствия между и (каждый элемент множества соответствует сам себе).

35. Примените эту конструкцию и явно укажите соответствие между отрезком и полуинтервалом .

36. Теорема 3 показывает, что добавление счетного множества к бесконечному не меняет его мощности. Можно ли сказать то же самое про удаление? Докажите, что если бесконечно и не является счетным, а конечно или счетно, то равномощно .

37. Немецкий математик Р.Дедекинд предложил такое определение бесконечного множества : множество бесконечно, если оно равномощно некоторому своему подмножеству, не совпадающему со всем множеством. Покажите, что указанное Дедекиндом свойство действительно определяет бесконечные множества .

Добавляя конечные или счетные множества , легко понять, что прямая, все промежутки на прямой (отрезки, интервалы, полуинтервалы), лучи, их конечные или счетные объединения и т.п. равномощны друг другу.

38. Укажите взаимно однозначное соответствие между множеством и отрезком .

39. Докажите, что множество всех прямых на плоскости равномощно множеству всех точек на плоскости. (Указание: и точки, и прямые задаются парами чисел - за небольшими исключениями.)

40. Докажите, что полуплоскость (точки плоскости, лежащие по одну сторону от некоторой прямой ) равномощна плоскости. (Это верно независимо от того, включаем мы граничную прямую в полуплоскость или нет.)

Теорема 4 . Отрезок равномощен множеству всех бесконечных последовательностей нулей и единиц.

Доказательство . В самом деле, каждое число записывается в виде бесконечной двоичной дроби. Первый знак этой дроби равен или в зависимости от того, попадает ли число в левую или правую половину отрезка. Чтобы определить следующий знак, надо выбранную половину поделить снова пополам и посмотреть, куда попадет , и т.д.

Это же соответствие можно описать в другую сторону: последовательности соответствует число, являющееся суммой ряда

(В этом построении мы используем некоторые факты из математического анализа, что не удивительно - нас интересуют свойства действительных чисел.)

Описанное соответствие пока что не совсем взаимно однозначно: двоично-рациональные числа (дроби вида ) имеют два представления. Например, число можно записать как в виде , так и в виде Соответствие станет взаимно однозначным, если отбросить дроби с единицей в периоде (кроме дроби , которую надо оставить). Но таких дробей счетное число, поэтому на мощность это не повлияет.

Какая двоичная дробь соответствует числу ?

В этом доказательстве можно было бы использовать более привычные десятичные дроби вместо двоичных. Получилось бы, что отрезок равномощен множеству всех бесконечных последовательностей цифр . Чтобы перейти отсюда к последовательностям нулей и единиц, можно воспользоваться приемом, описанным ранее.

Теперь все готово для доказательства такого удивительного факта:

Теорема 5 . Квадрат (со внутренностью) равномощен отрезку.

Доказательство . Квадрат равномощен множеству пар действительных чисел, каждое из которых лежит на отрезке (метод координат). Мы уже знаем, что вместо чисел на отрезке можно говорить о последовательностях нулей и единиц. Осталось заметить, что паре последовательностей нулей и единиц можно поставить в соответствие последовательность-смесь и что это соответствие будет взаимно однозначным.

Этот результат был получен в 1877 году немецким математиком Георгом Кантором и удивил его самого, поскольку противоречил интуитивному ощущению " размерности" (квадрат двумерен, поэтому вроде бы должен содержать больше точек, чем одномерный отрезок ). Вот что Кантор писал Дедекинду (20 июня 1877 года), обсуждая вопрос о равномощности пространств разного числа измерений: " Как мне кажется, на этот вопрос следует ответить утвердительно, хотя на протяжении ряда лет я придерживался противоположного мнения".