Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. а в А В = 2 c
Доказательство: A B CD M N 1 2 A B CD M N 1 2 K O Пусть прямые АВ и СD параллельны, МN их секущая. Докажем, что накрест лежащие углы 1 и 2 равны между собой. Допустим, что 1 и 2 не равны. Проведем через точку О прямую КF. Тогда при точке О можно построить KON, накрест лежащий и равный 2. Но если KON = 2, то прямая КF будет параллельна СD. Получили, что через точку О проведены две прямые АВ и КF, параллельные прямой СD. Но этого не может быть. Мы пришли к противоречию, потому что допустили, что 1 и 2 не равны. Следовательно, наше допущение является неправильным и 1 должен быть равен 2, т. е. накрест лежащие углы равны. F
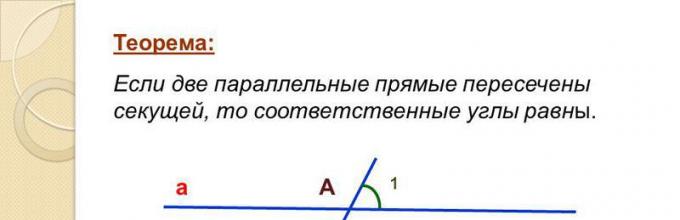
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равны. а в А В = 2
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. а в А В = 180°
Доказательство: Пусть параллельные прямые а и b пересечены секущей АВ, то соответственные 1 и 2 будут равны, 2 и 3 – смежные, поэтому = 180°. Из равенств 1 = 2 и = 180° следует, что = 180°. Теорема доказана. 2 а в А В 3 1
Решение: 1. Пусть Х – это 2, тогда 1 = (Х+70°), т.к. сумма углов 1 и 2 = 180°, в силу того, что они смежные. Составим уравнение: Х+ (Х+70°) = 180° 2Х = 110 ° Х = 55° (Угол 2) 2. Найдем 1. 55° + 70° = 125° 3. 1 = 3, т.к. они вертикальные. 3 = 5, т.к. они накрест лежащие. 125° 5 = 7, т.к. они вертикальные. 2 = 4, т.к. они вертикальные. 4 = 6, т.к. они накрест лежащие. 55° 6 = 8, т.к. они вертикальные. Задача 1: A B Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.
Решение: 1. 1= 2, т.к. они вертикальные, значит 2= 45° смежен с 2, поэтому 3+ 2=180°, и из этого следует, что 3= 180° - 45°= 135° =180°, т.к. они односторонние. 4 = 45°. Ответ: 4=45°; 3=135°. Задача 3: A B 2 Условие: две параллельные прямые А и B пересечены секущей С. Найти, чему будут равны 4 и 3, если 1=45°
Теорема: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. а в А В 1 2 1 = 2 c
Доказательство: A B C DM N 1 2 K O Пусть прямые АВ и СD параллельны, МN - их секущая. Докажем, что накрест лежащие углы 1 и 2 равны между собой. Допустим, что 1 и 2 не равны. Проведем через точку О прямую К F. Тогда при точке О можно построить KON , накрест лежащий и равный 2. Но если KON = 2, то прямая К F будет параллельна СD. Получили, что через точку О проведены две прямые АВ и К F, параллельные прямой СD. Но этого не может быть. Мы пришли к противоречию, потому что допустили, что 1 и 2 не равны. Следовательно, наше допущение является неправильным и 1 должен быть равен 2, т. е. накрест лежащие углы равны.
Теорема: Если две параллельные прямые пересечены секущей, то соответственные углы равн ы. а в А В 1 2 1 =
Доказательство: 2 а в А В 3 1 Пусть параллельные прямые а и b пересечены секущей АВ, то накрест лежащие 1 и 3 будут равны. 2 и 3 равны как вертикальные. Из равенств 1 = 3 и 2 = 3 следует, что 1 = 2. Теорема доказана
Теорема: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. а в А В 3 1 1 + 3 = 180°
Доказательство: Пусть параллельные прямые а и b пересечены секущей АВ, то соответственные 1 и 2 будут равны, 2 и 3 – смежные, поэтому 2 + 3 = 180 °. Из равенств 1 = 2 и 2 + 3 = 180 ° следует, что 1 + 3 = 180 °. Теорема доказана. 2 а в А В
Решение: 1. Пусть Х – это 2, тогда 1 = (Х+70°), т. к. сумма углов 1 и 2 = 180°, в силу того, что они смежные. Составим уравнение: Х+ (Х+70°) = 180° 2 Х = 110 ° Х = 55° (Угол 2) 2. Найдем 1. 55° + 70° = 125° 3. 1 = 3, т. к. они вертикальные. 3 = 5, т. к. они накрест лежащие. 125° 5 = 7, т. к. они вертикальные. 2 = 4, т. к. они вертикальные. 4 = 6, т. к. они накрест лежащие. 55° 6 = 8, т. к. они вертикальные. Задача № 1: A B 4 3 5 8 7 21 6 Условие: найдите все углы, образованные при пересечении двух параллельных A и B секущей C, если один из углов на 70° больше другого.
Решение: 1. Т. к. 4 = 45°, то 2 = 45°, потому что 2 = 4(как соответственные) 2. 3 смежен с 4, поэтому 3+ 4=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 1 = 3, т. к. они накрест лежащие. 1 = 135°. Ответ: 1=135°; 2=45°; 3=135°. Задача № 2: A B 1 Условие: на рисунке прямые А II B и C II D, 4=45°. Найти углы 1, 2, 3.
Решение: 1. 1= 2, т. к. они вертикальные, значит 2= 45°. 2. 3 смежен с 2, поэтому 3+ 2=180°, и из этого следует, что 3= 180° — 45°= 135°. 3. 4 + 3=180°, т. к. они односторонние. 4 = 45°. Ответ: 4=45°; 3=135°. Задача № 3: A B 2 Условие: две параллельные прямые А и B пересечены секущей С. Найти, чему будут равны 4 и 3, если 1=45°.
\[{\Large{\text{Центральные и вписанные углы}}}\]
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
Треугольник \(AOB\) – равнобедренный, \(AO = OB\) , \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\) , откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\) .
Теперь рассмотрим произвольный вписанный угол \(ABC\) . Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\) (для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\) , у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
\[{\Large{\text{Касательная к окружности}}}\]
Определения
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\) :
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\) .
Следствие
Центр окружности \(O\) лежит на биссектрисе угла \(AKB\) , образованного двумя касательными, проведенными из одной точки \(K\) .
\[{\Large{\text{Теоремы, связанные с углами}}}\]
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} - \buildrel\smile\over{CA})\) .
\(\angle DAB\) – внешний угол треугольника \(MAD\) , тогда \(\angle DAB = \angle DMB + \angle MDA\) , откуда \(\angle DMB = \angle DAB - \angle MDA\) , но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB - \angle MDA = \frac{1}{2}\buildrel\smile\over{BD} - \frac{1}{2}\buildrel\smile\over{CA} = \frac{1}{2}(\buildrel\smile\over{BD} - \buildrel\smile\over{CA})\) , что и требовалось доказать.
Теорема об угле между пересекающимися хордами
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]
Доказательство
\(\angle BMA = \angle CMD\) как вертикальные.
Из треугольника \(AMD\) : \(\angle AMD = 180^\circ - \angle BDA - \angle CAD = 180^\circ - \frac12\buildrel\smile\over{AB} - \frac12\buildrel\smile\over{CD}\) .
Но \(\angle AMD = 180^\circ - \angle CMD\) , откуда заключаем, что \[\angle CMD = \frac12\cdot\buildrel\smile\over{AB} + \frac12\cdot\buildrel\smile\over{CD} = \frac12(\buildrel\smile\over{AB} + \buildrel\smile\over{CD}).\]
Теорема об угле между хордой и касательной
Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.
Доказательство
Пусть прямая \(a\) касается окружности в точке \(A\) , \(AB\) – хорда этой окружности, \(O\) – её центр. Пусть прямая, содержащая \(OB\) , пересекает \(a\) в точке \(M\) . Докажем, что \(\angle BAM = \frac12\cdot \buildrel\smile\over{AB}\) .
Обозначим \(\angle OAB = \alpha\) . Так как \(OA\) и \(OB\) – радиусы, то \(OA = OB\) и \(\angle OBA = \angle OAB = \alpha\) . Таким образом, \(\buildrel\smile\over{AB} = \angle AOB = 180^\circ - 2\alpha = 2(90^\circ - \alpha)\) .
Так как \(OA\) – радиус, проведённый в точку касания, то \(OA\perp a\) , то есть \(\angle OAM = 90^\circ\) , следовательно, \(\angle BAM = 90^\circ - \angle OAB = 90^\circ - \alpha = \frac12\cdot\buildrel\smile\over{AB}\) .
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
1) Пусть \(AB=CD\) . Докажем, что меньшие полуокружности дуги .
По трем сторонам, следовательно, \(\angle AOB=\angle COD\) . Но т.к. \(\angle AOB, \angle COD\) - центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB}, \buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\) .
2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\) , то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\) . Следовательно, и \(AB=CD\) .
Теорема
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
Доказательство
1) Пусть \(AN=NB\) . Докажем, что \(OQ\perp AB\) .
Рассмотрим \(\triangle AOB\) : он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\) .
2) Пусть \(OQ\perp AB\) . Докажем, что \(AN=NB\) .
Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\) .
\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\) .
Рассмотрим треугольники \(ADE\) и \(CBE\) . В этих треугольниках углы \(1\) и \(2\) равны, так как они вписанные и опираются на одну и ту же дугу \(BD\) , а углы \(3\) и \(4\) равны как вертикальные. Треугольники \(ADE\) и \(CBE\) подобны (по первому признаку подобия треугольников).
Тогда \(\dfrac{AE}{EC} = \dfrac{DE}{BE}\) , откуда \(AE\cdot BE = CE\cdot DE\) .
Теорема о касательной и секущей
Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.
Доказательство
Пусть касательная проходит через точку \(M\) и касается окружности в точке \(A\) . Пусть секущая проходит через точку \(M\) и пересекает окружность в точках \(B\) и \(C\) так что \(MB < MC\) . Покажем, что \(MB\cdot MC = MA^2\) .
Рассмотрим треугольники \(MBA\) и \(MCA\) : \(\angle M\) – общий, \(\angle BCA = 0,5\cdot\buildrel\smile\over{AB}\) . По теореме об угле между касательной и секущей, \(\angle BAM = 0,5\cdot\buildrel\smile\over{AB} = \angle BCA\) . Таким образом, треугольники \(MBA\) и \(MCA\) подобны по двум углам.
Из подобия треугольников \(MBA\) и \(MCA\) имеем: \(\dfrac{MB}{MA} = \dfrac{MA}{MC}\) , что равносильно \(MB\cdot MC = MA^2\) .
Следствие
Произведение секущей, проведённой из точки \(O\) , на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\) .
Видеоурок о теоремах об углах между двумя параллельными прямыми и их секущей содержит материал, представляющий особенности строения теоремы, примеры формирования и доказательства обратных теорем, следствий из них. Задача данного видеоурока - углубить понятие теоремы, разложив ее на составляющие, рассмотрев понятие обратной теоремы, формировать умение строить теорему, обратную данной, следствий из теоремы, формировать умение доказывать утверждения.
Форма видеоурока позволяет удачно расставить акценты при демонстрации материала, облегчая понимание и запоминание материала. Тема данного видеоурока сложная и важная, поэтому использование наглядного пособия не только целесообразно, но и желательно. Он дает возможность повысить качество обучения. Анимированные эффекты улучшают представление учебного материала, приближают процесс обучения к традиционному, а использование видео освобождает учителя для углубления индивидуальной работы.
Видеоурок начинается с объявления его темы. В начале урока рассматривается разложение теоремы на составляющие для лучшего понимания ее строения и возможностей для дальнейшего исследования. На экране демонстрируется схема, демонстрирующая, что теорема состоит их условия и заключения. Понятие условия и заключения описывается на примере признака параллельности прямых, отметив, что часть утверждения является условием теоремы, а вывод - заключением.
Углубляя полученные знания о строении теоремы, ученикам дается понятие теоремы, обратной данной. Она образуется в результате замены - условие становится заключением, заключение - условием. Чтобы сформировать умение учеников строить теоремы, обратные данным, умение доказывать их, рассматриваются теоремы, обратные тем, которые рассмотрены в уроке 25 о признаках параллельности прямых.
На экране отображается теорема, обратная первой теореме, описывающей признак параллельный прямых. Поменяв местами условие и заключение, получаем утверждение, что если пересечены секущей какие-либо параллельные прямые, то образованные при этом накрест лежащие углы будут равными. Доказательство демонстрируется на рисунке, где изображены прямые а, b, а также секущая, проходящая через эти прямые в их точках M и N. На изображении отмечаются накрест лежащие углы ∠1 и ∠2. Необходимо доказать их равенство. Сначала в ходе доказательства делается предположение, что данные углы не являются равными. Для этого через точку М проводится некоторая прямая Р. Строится угол `∠PMN, являющийся накрест лежащим с углом ∠2 по отношению к MN. Углы `∠PMN и ∠2 по построению равны, следовательно МР║b. Вывод - через точку проведены две прямые, параллельные b. Однако это невозможно, потому что не соответствует аксиоме параллельных прямых. Сделанное предположение оказывается ошибочным, доказывая справедливость изначального утверждения. Теорема доказана.
Далее обращается внимание учеников на способ доказательства, который был использован в ходе рассуждений. Доказательство, в котором предполагается ошибочность доказываемого утверждения, называется в геометрии доказательством от противного. Данный способ часто используется для доказательства различных геометрических утверждений. В данном случае, предположив, неравенство накрест лежащих углов, в ходе рассуждений выявилось противоречие, что отрицает справедливость такого противоречия.
Ученикам напоминается, что подобный способ уже был использован ранее в доказательствах. Примером этому служит доказательство теоремы в уроке 12 о том, что две прямые, которые перпендикулярны третьей, не пересекаются, а также доказательства следствий в уроке 28 из аксиомы параллельности прямых.
Еще одно доказываемое следствие утверждает, что прямая перпендикулярна к обеим параллельным прямым, если она перпендикулярна к одной из них. На рисунке изображаются прямые а и b и перпендикулярная им прямая с. Перпендикулярность прямой c к а означает, что образуемый с ней угол равен 90°. Параллельность а и b, пересечение их прямой с означает, что прямая с пересекает b. Угол ∠2, образованный с прямой b, является накрест лежащим к углу ∠1. А так как по условию прямые параллельны, то данные углы равны. Соответственно, величина угла ∠2 также будет равна 90°. Это означает, прямая с оказалась перпендикулярной прямой b. Рассматриваемая теорема доказана.
Следующей доказывается теорема, обратная ко второму признаку параллельных прямых. Обратная теорема утверждает, при условии параллельности двух прямых образованные соответственные углы будут равными. Доказательство начинается с построения секущей с, параллельных между собой прямых а и b. Созданные при этом углы отмечаются на рисунке. Имеется пара соответственных углов, названные ∠1 и ∠2, также отмечен угол ∠3, который накрест лежащий углу ∠1. Параллельность а и b означает равенство ∠3=∠1 как накрест лежащих. Учитывая, что ∠3, ∠2 - вертикальные, они также равны. Следствием таких равенств является утверждение, что ∠1=∠2. Рассматриваемая теорема доказана.
Последняя доказываемая на данном уроке теорема - обратная последнему признаку параллельных прямых. Ее текст гласит, что в случае прохождения через параллельные прямые некоторой секущей, сумма образованных при этом односторонних углов равна величине в 180°. Ход доказательства демонстрируется на рисунке, где изображены прямые а и b, пересекающиеся с секущей с. Необходимо доказать, что величина суммы односторонних углов будет равняться 180°, то есть ∠4+∠1 = 180°. Из параллельности прямых а и b следует равенство соответственных углов ∠1 и ∠2. Смежность углов ∠4, ∠2 означает, что в сумме они составляют 180°. При этом углы ∠1= ∠2 - значит, ∠1 в сумме с углом ∠4 будет составлять 180°. Теорема доказана.
Для более глубокого понимания, как формируются и доказываются обратные теоремы, отдельно отмечается, что если теорема доказана и верна, то это не значит, что также верна будет обратная теорема. Чтобы это понять, приводится простой пример. Есть теорема о том, что все вертикальные углы равны. Обратная теорема звучит так, что все равные углы вертикальны, что не соответствует действительности. Ведь можно построить два равных угла, которые не будут вертикальны. Это можно увидеть на продемонстрированном рисунке.
Видеоурок «Теоремы об углах, образованных двумя параллельными прямыми и секущей» является наглядным пособием, которое может быть использовано учителем на уроке геометрии, а также успешно сформировать представление об обратных теоремах и следствиях, а также их доказательстве при самостоятельном изучении материала, быть полезным в дистанционном обучении.
