17.03.2019

Взаимное расположение прямой и окружности три случая. Учебный лист по геометрии "Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей" (7 класс). Приумножать их – мудрость

В данном уроке мы изучим различные варианты взаимодействия окружности и прямой. Напомним определения, широко используемые в этом случае. Прямой называется неопределяемая аксиоматическая геометрическая фигура, представляющая собой ровную прямую линию без начала и конца. Окружностью именуется множество точек, равноудаленно лежащих от общего центра (центра окружности), соединенных общей кривой. Иначе говоря, окружность - это правильная замкнутая кривая, обрисовывающая максимально возможную площадь.

Собственно говоря, существуют три варианта взаимного расположения окружности и прямой. В первом случае, прямая пролегает полностью вне заданной окружности, нигде её не пересекая и не затрагивая. Если же прямая затрагивает ровно одну определенную точку из множества на окружности, то эта линия именуется касательной, по отношению к данной окружности.

Касательная имеет одно важнейшее свойство. Радиус, проведенный к точке касания, является перпендикуляром к самой прямой. На видео представлена окружность с центром О, прямой А и точкой касания К. Так как эта точка в единственном числе, то прямая А касательна данной окружности. А угол при К, образованный радиусом и любой частью прямой, является прямым - равен 90 градусам. Стоит также отметить важную особенность - касательная имеет исключительно одну точку касания. Невозможно провести прямую так, чтобы касательно затронуть две точки на окружности.
Если же наша прямая А проходит через всю окружность, затрагивая её внутреннюю область, то это уже третий частный случай взаимодействия данных фигур. При этом, прямая проходит строго через две точки на окружности - скажем, В и С. Она именуется секущей окружности. Секущая всегда проходит только через две любые точки из множества на кривой. Так как точек в окружности множество, то реализуемо провести бесконечное число секущих (равно как и касательных) для заданной окружности.

Внутренняя часть секущей прямой, по сути отрезок ВС, является хордой для окружности. Если секущая проходит через центр окружности, то внутренняя ее часть представлена наибольшей хордой - диаметром. При этом, точки пересечения В и С находятся на наибольшем удалении друг от друга (по свойству диаметра). Легко понять, что противоположный частный случай - это секущая, образующая хорду с бесконечно малым значением, по сути, - это уже касательная.

В задачах часто встречается отрезок Р - он соединяет наиболее коротким путем подходящую точку на прямой и центр самой окружности. Иначе говоря, Р - это отрезок ТО, где Т - точка на прямой ВС. Этот отрезок является перпендикуляром для прямой, его продолжение до самой окружности - ее радиусом. Линейное значение этого отрезка можно вычислить через косинус угла, образованного радиусом и секущей прямой, с вершиной в точке сечения.

Возьмем произвольную окружность с центром в точке О и прямую a.
Если прямая a пройдет через точку O, то она пересечет данную окружность в двух точках K и L, которые являются концами диаметра, лежащего на прямой а.

Если прямая a не будет проходить через центр О окружности, то выполним вспомогательное построение и проведем прямую OH перпендикулярно прямой a и обозначим полученное расстояние от центра окружности до прямой a переменной rasstoyanie. Определим, сколько будет общих точек у прямой a и окружности в зависимости от соотношения между переменной rasstoyanie и radius.
Может быть 3 варианта:

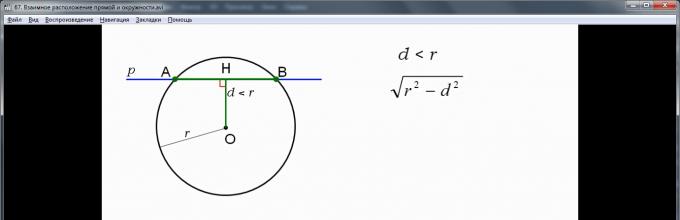
rasstoyanie < radius . В таком случае точка H будет лежать в середине круга, который ограничен данной окружностью.

Отложим на прямой а отрезок HD = r adius .

В OHD гипотенуза OD больше катета HD , поэтому OD > r adius . Следовательно, точка D лежит за кругом, который ограничен данной окружностью. Значит, один конец отрезка HD находится в середине круга, а другой – за кругом. Таким образом, на отрезке HD можно обозначить точку A , которая лежит на окружности, то есть OA = r adius .

Продлим луч HA и отложим на нем отрезок BН , который равен отрезку AН.

Получены 2 прямоугольных треугольника OHA и OHB , которые равны по двум катетам. Тогда их соответствующие стороны равны: OB = OA = r . Следовательно, B тоже является общей точкой окружности и прямой. Так как 3 точки окружности не могут лежать на одной прямой, то другие общие точки прямой a и окружности не существуют.
Таким образом, если расстояние между центром окружности и прямой меньше от радиуса окружности (rasstoyanie < r adius ), то у прямой и окружности 2 общие точки.

rasstoyanie = r adius . Поскольку OH = r adius , то точка H принадлежит окружности и, поэтому, является общей точкой для прямой a и окружности.

Для любых других точек прямой a (например, точки и M ) наклонная OM больше отрезка OH , то есть OM > OH = r adius , и следовательно точка M не принадлежит заданной окружности.
Следовательно, если расстояние между центром окружности и прямой равно радиусу окружности (rasstoyanie = r adius ), то у прямой и окружности лишь одна общая точка.

rasstoyanie > r adius . Так как OH > radius, то для любых точек прямой a (например, точки M ) выполняется неравенство OM > OH > r adius . Таким образом, точка M не принадлежит окружности.

Следовательно, если расстояние между центром окружности и прямой больше от радиуса окружности (rasstoyanie > r adius ), то у прямой и окружности нет общих точек.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ ГЕОМЕТРИЯ 8 класс по учебнику Л.А.Атанасяна

Как вы думаете, сколько общих точек могут иметь прямая и окружность? О

О Сначала вспомним как задаётся окружность Окружность (О, r) r – радиус r A B АВ – хорда С D CD - диаметр

Исследуем взаимное расположение прямой и окружности в первом случае: d – расстояние от центра окружности до прямой О А В Н d

Второй случай: О Н r одна общая точка d = r d – расстояние от центра окружности до прямой d

Третий случай: О H d r d > r d – расстояние от центра окружности до прямой не имеют общих точек

Сколько общих точек могут иметь прямая и окружность? d r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Касательная к окружности Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. O s = r M m

Выясните взаимное расположение прямой и окружности, если: r = 15 см, s = 11 см r = 6 см, s = 5 ,2 см r = 3,2 м, s = 4 ,7 м r = 7 см, s = 0,5 дм r = 4 см, s = 4 0 мм прямая – секущая прямая – секущая общих точек нет прямая – секущая прямая - касательная

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. m – касательная к окружности с центром О М – точка касания OM - радиус O M m

Свойство касательных, проходящих через одну точку: ▼ По свойству касательной ∆ АВО, ∆ АСО–прямоугольные ∆ АВО= ∆ АСО–по гипотенузе и катету: ОА – общая, ОВ=ОС – радиусы АВ=АС и ▲ О В С А 1 2 3 4 Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной. окружность с центром О радиуса OM m – прямая, которая проходит через точку М и m – касательная O M m

Решите № 633. Дано: OABC- квадрат AB = 6 см Окружность с центром O радиуса 5 см Найти: секущие из прямых OA , AB , BC , АС О А В С О

Решите № 638, 640. д/з: выучить конспект, № 631, 635

По теме: методические разработки, презентации и конспекты

Цель: закрепить умение определять взаимное расположение прямой и плоскости, проверить навыки решения задач, воспитывать чувство коллективизма. ...

взаимное расположение прямой и окружности. 8класс.

В презентацию помещены четыре устные задачи, решаемые по готовым чертежам. Цель: подготовить учащихся к изучению нового материала....

Взаимное расположение прямой и окружности. Взаимное расположение двух ркружностей.

Конспект и презентация к уроку по теме "Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей". Урок в 6 классе по учебнику "Математика - 6" под ред. Г.В. Дорофеев, И...

Пусть на плоскости даны окружность и некоторая прямая. Опустим на эту прямую перпендикуляр из центра окружности С; обозначим через основание этого перпендикуляра. Точка может занимать относительно окружности три возможных положения: а) лежать вне окружности, б) на окружности, в) внутри окружности. В зависимости от этого и прямая будет занимать относительно окружности одно из трех возможных различных положений, описываемых ниже.

а) Пусть основание перпендикуляра опущенного из центра С окружности на прямую а, лежит вне окружности (рис. 197). Тогда прямая не пересекает окружности, все ее точки лежат во внешней области. Действительно, в указанном случае по условию удалена от центра на расстояние, большее радиуса). Тем более для любой точки М прямой а имеем т. е. каждая точка данной прямой лежит вне круга.

б) Пусть основание перпендикуляра попадет на окружность (рис. 198). Тогда прямая а имеет с окружностью ровно одну общую точку . Действительно, если М - любая другая точка прямой, то (наклонные длиннее перпендикуляра) и точка М лежит во внешней области. Такая прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности в этой точке. Покажем, что и обратно, если прямая имеет с окружностью единственную общую точку, то радиус, проведенный в эту точку, перпендикулярен к данной прямой. Действительно, опустим из центра перпендикуляр на данную прямую. Если бы его основание лежало внутри окружности, то прямая имела бы с ней, как показано в в), две общие точки. Если бы оно лежало вне окружности, то в силу а) прямая не имела бы с окружностью общих точек.

Поэтому остается допустить, что перпендикуляр попадает в общую точку прямой и окружности - в точку их касания. Доказана важная

Теорема. Прямая, проходящая через точку окружности, тогда и только тогда касается окружности, когда она перпендикулярна к радиусу, проведенному в эту точку.

Заметим, что определение касательной к окружности, данное здесь, не переносится на другие кривые. Более общее определение касательной прямой к кривой линии связано с понятиями теории пределов и рассматривается подробно в курсе высшей математики. Здесь мы дадим о нем только общее понятие. Пусть даны окружность и на ней точка А (рис. 199).

Возьмем еще точку А на окружности и соединим обе точки прямой АА. Пусть точка А двигаясь по окружности, занимаетпоследовательно ряд новых положений приближаясь все больше к точке А. Прямая АА, вращаясь вокруг А, принимает ряд положений: при этом по мере сближения движущейся точки с точкой А прямая стремится к совпадению с касательной АТ. Поэтому можно говорить о касательной как о предельном положении секущей, проходящей через данную точку и точку кривой, неограниченно с ней сближающуюся. В такой форме определение касательной применимо к кривым весьма общего вида (рис. 200).

в) Пусть, наконец, точка лежит внутри окружности (рис. 201). Тогда . Будем рассматривать наклонные, проведенные к прямой а из центра С окружности, с основаниями удаляющимися от точки в любом из двух возможных направлений. Длина наклонной будет монотонно возрастать по мере удаления ее основания от точки это возрастание длины наклонной происходит постепенно («непрерывно») от значений, близких к до значений, сколь угодно больших, поэтому кажется ясным, что при некотором положении оснований наклонных длина их будет точно равна соответствующие точки К и L прямой будут лежать на окружности.

Составила учитель математики

МБОУ СШ №18 г. Красноярск

Андреева Инга Викторовна

Взаимное расположение прямой и окружности

О R – радиус

С D – диаметр

AB - хорда

Окружность с центром в точке О радиуса r
Прямая, которая не проходит через центр О
Расстояние от центра окружности до прямой обозначим буквой s

Возможны три случая:

1) s

меньше радиуса окружности, то прямая и окружность имеют две общие точки .

Прямая АВ называется секущей по отношению к окружности.

Возможны три случая:

2 ) s = r

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .

s = r

r Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек. sr r O" width="640"

Возможны три случая:

3 ) sr

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Касательная к окружности

Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

s = r