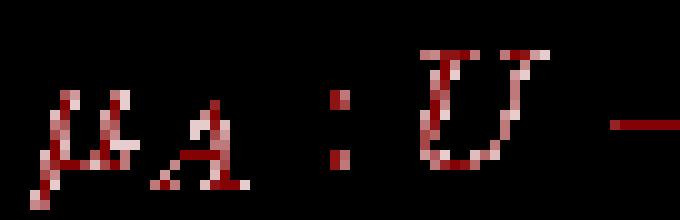(предпосылок) к новым суждениям - заключениям.

Правила преобразования исходной системы предпосылок в систему заключений называются правилами вывода или правилами проведения умозаключений . Если вид посылок и заключений указан явно, то вывод называется прямым . Если в посылках и заключении указаны лишь виды выводов, от одного из которых разрешается переходить к другому, то вывод называют косвенным .

Понятие вывода используется во многих формальных системах: в логике , математике , информатике , логическом программировании и др. В математической логике правила логического вывода задаются в исчисленн высказываний либо исчислении предикатов.

В информатике вывод умозаключений проводится с использованием правил, принципов и законов логического вывода на основе заданных фактов и правил с использованием методов и средств логического программирования.

Умозаключения (отдельные шаги вывода) разделяют:
1)по направлению логического следования на

дедуктивные (от общего к частному)
индуктивные (от частного к общему)
трансдуктивные (от общего к общему)

2)по достоверности вывода на

достоверные
правдоподобные

3)по числу посылок

непосредственные
опосредственные

Wikimedia Foundation . 2010 .

Логический атомизм
Логический круг

Смотреть что такое "Логический вывод" в других словарях:

логический вывод - — Тематики электросвязь, основные понятия EN inference … Справочник технического переводчика

ЕСТЕСТВЕННЫЙ ЛОГИЧЕСКИЙ ВЫВОД - формальный вывод, по возмвжности приближенный к содержательному рассуждению, привычному для математика и логика. Критерии естественности и качества вывода не уточняются полностью, но обычно имеются в виду выводы, осуществляемые по… … Математическая энциклопедия

ВЫВОД ЛОГИЧЕСКИЙ - ВЫВОД ЛОГИЧЕСКИЙ рассуждение, в котором осуществляется переход по правилам от высказывания или системы высказываний к высказыванию или системе высказываний. К логическому выводу обычно предъявляются (совместно или по отдельности)… … Философская энциклопедия

ВЫВОД - логический формальный вывод в исчислении, содержащем логические правила и имеющем в качестве основных выводимых объектов формулы (интерпретацией к рых являются суждения;см. Логические исчисления. Логико математические исчисления). Поскольку… … Математическая энциклопедия

ЛОГИЧЕСКИЙ - ЛОГИЧЕСКИЙ, логическая, логическое (книжн.). 1. прил. к логика. Логические категории. 2. (в качестве кратк. употр. логичен, логична, логично). Основанный на правильном умозаключении, отвечающий требованиям логики. Логический вывод. Логическое… … Толковый словарь Ушакова

Вывод - может употребляться в разных контекстах: Вывод проводник в составе электрического устройства, предназначенный для электрического соединения с другими устройствами Устройства ввода вывода класс устройств в типовой архитектуре ЭВМ Вывод результат… … Википедия

логический - прил., употр. сравн. часто Морфология: нар. логически 1. Логическим называют что либо, имеющее отношение к логике как науке. Логические категории. | Логические законы. 2. Логическим называют что либо согласующееся с законами логики, основанное на … Толковый словарь Дмитриева

вывод - сущ., м., употр. часто Морфология: (нет) чего? вывода, чему? выводу, (вижу) что? вывод, чем? выводом, о чём? о выводе; мн. что? выводы, (нет) чего? выводов, чему? выводам, (вижу) что? выводы, чем? выводами, о чём? о выводах 1. Когда вы приходите… … Толковый словарь Дмитриева

ЛОГИЧЕСКИЙ - (греч. logikos, от logos рассуждение). Согласный с логикою или основанный на законах мышления. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ЛОГИЧЕСКИЙ греч. logikos, от logos, рассуждение. Согласный или… … Словарь иностранных слов русского языка

вывод логический - ВЫВОД ЛОГИЧЕСКИЙ рассуждение, в котором по определенным правилам осуществляется переход от высказываний или системы высказываний к высказыванию или системе высказываний. К В. л. обычно предъявляются (разом или по отдельности) следующие… … Энциклопедия эпистемологии и философии науки

Книги

Искусственный интеллект. Современный подход. Руководство , Норвиг Питер. Первое издание этой книги стало классическим образцом литературы по искусственному интеллекту. Оно было принято в качестве учебного пособия больше чем в 600 университетах 60 стран мира и…

5 января 2011 в 01:28

Прямой нечеткий логический вывод

Алгоритмы

Введение

В 1965 г. в журнале «Information and Control» была опубликована работа Л.Заде под названием «Fuzzy sets». Это название переведено на русский язык как нечеткие множества . Побудительным мотивом стала необходимость описания таких явлений и понятий, которые имеют многозначным и неточный характер. Известные до этого математические методы, использовавшие классическую теорию множеств и двузначную логику, не позволяли решать проблемы этого типа.

При помощи нечетких множеств можно формально определить неточные и многозначные понятия, такие как «высокая температура» или «большой город». Для формулирования определения нечеткого множества необходимо задать так называемую област рассуждений. Например, когда мы оцениваем скорость автомобиля, мы ограничимся диапазоном X = , где Vmax - максимальная скорость, которую может развить автомобиль. Необходимо помнить, что X - четкое множество.

Основные понятия

Нечетким множеством A в некотором непустом пространстве X называется множество пар

Где

- функция принадлежности нечеткого множества A. Эта функция приписывает каждому элементу x степень его принадлежности нечеткому множеству A.

Продолжив предыдущий пример, рассмотрим три неточные формулировки:
- «Малая скорость автомобиля»;
- «Средняя скорость автомобиля»;
- «Большая скорость автомобиля».
На рисунке представлены нечеткие множества, соответствующие приведенным формулировкам, с помощью функций принадлежности.

В фиксированной точке X=40км/ч. функция принадлежности нечеткого множества «малая скорость автомобиля» принимает значением 0,5. Такое же значение принимает функция принадлежностинечеткого множества «средняя скорость автомобиля», тогда как для множества «большая скорость автомобиля» значение функции в этой точке равно 0.

Функция T двух переменных T: x -> называется T-нормой , если:
- является не возрастающей относительно обоих аргументов: T(a, c) < T(b, d) для a < b, c < d;
- является коммутативной: T(a, b) = T(b, a);
- удовлетворяет условию связности: T(T(a, b), c) = T(a, T(b, c));
- удовлетворяет граничным условиям: T(a, 0) = 0, T(a, 1) = a.

Прямой нечеткий вывод

Под нечетким выводом понимается процесс, при котором из нечетких посылок получают некоторые следствия, возможно, тоже нечеткие. Приближенные рассуждения лежат в основе способности человека понимать естественный язык, разбирать почерк, играть в игры, требующие умственных усилий, в общем, принимать решения в сложной и не полностью определенной среде. Эта способность рассуждений в качественных, неточных терминах отличает интеллект человека от интеллекта вычислительной машины.

Основным правилом вывода в традиционной логике является правило modus ponens, согласно которому мы судим об истинности высказывания B по истинности высказываний A и A -> B. Например, если A - высказывание «Степан - космонавт», B - высказывание «Степан летает в космос», то если истинны высказывания «Степан - космонавт» и «Если Степан - космнавт, то он летает в космос», то истинно и высказывание «Степан летает в космос».

Однако, в отличие от традиционной логики, главным инструментом нечеткой логики будет не правило modus ponens, а так называемое композиционное правило вывода, весьма частным случаем которого является правило modus ponens.

Предположим, что имеется кривая y=f(x) и задано значение x=a. Тогда из того, что y=f(x) и x=a, мы можем заключить, что y=b=f(a).

Обобщим теперь этот процесс, предположив, что a - интервал, а f(x) - функция, значения которой суть интервалы. В этом случае, чтобы найти интервал y=b, соответствующий интервалу a, мы сначала построим множество a" с основанием a и найдем его пересечение I с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось OY и получим желаемое значение y в виде интервала b. Таким образом, из того, что y=f(x) и x=A - нечеткое подмножество оси OX, мы получаем значение y в виде нечеткого подмножества B оси OY.

Пусть U и V - два универсальных множества с базовыми переменными u и v, соответственно. Пусть A и F - нечеткие подмножества множеств U и U x V. Тогда композиционное правило вывода утверждает, что из нечетких множеств A и F следует нечеткое множество B = A * F.

Пусть A и B - нечеткие высказывания и m(A), m(B) - соответствующие им функции принадлежности. Тогда импликации A -> B будет соответствовать некоторая функция принадлежности m(A -> B). По аналогии с традиционной логикой, можно предположить, что

Тогда

Однако, это не единственное обобщение оператора импликации, существуют и другие.

Реализация

Для реализации метода прямого нечеткого логического вывода нам понадобится выбрать оператор импликации и T-норму.
Пуская T-норма будет функция минимума:

а оператором импликации будет функция Гёделя:

Входные данные будут содержать знания (нечеткие множества) и правила (импликации), например:
A = {(x1, 0.0), (x2, 0.2), (x3, 0.7), (x4, 1.0)}.
B = {(x1, 0.7), (x2, 0.4), (x3, 1.0), (x4, 0.1)}.
A => B.

Импликация будет представлена в виде декартовой матрицы, каждый элемент которой рассчитывается с помощью выбранного оператора импликации (в данном примере - функции Гёделя):

def compute_impl (set1, set2):

"""
Computing implication
"""

relation = {}

for i in set1.items():

relation[i] = {}

for j in set2.items():

v1 = set1.value(i)

v2 = set2.value(j)

relation[i][j] = impl(v1, v2)

return relation

Для данных выше это будет:
Conclusion:
A => B.
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1

def conclusion (set, relation):

"""
Conclusion
"""

conl_set =

for i in relation:

l =

for j in relation[i]:

v_set = set .value(i)

v_impl = relation[i][j]

l.append(t_norm(v_set, v_impl))

value = max (l)

conl_set.append((i, value))

return conl_set

Результат:
B" = {(x1, 1.0), (x2, 0.7), (x3, 1.0), (x4, 0.7)}.

Источники

Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. - М.: Горячая линия - Телеком, 2006. - 452 с.: ил.
Zadeh L. A. Fuzzy Sets, Information and Control, 1965, vol. 8, s. 338-353

Основные понятия

Нечетким множеством A в некотором непустом пространстве X называется множество пар

Прямой нечеткий вывод

Реализация

def compute_impl (set1, set2):

"""
Computing implication
"""

relation = {}

for i in set1.items():

relation[i] = {}

for j in set2.items():

v1 = set1.value(i)

v2 = set2.value(j)

relation[i][j] = impl(v1, v2)

return relation

Для данных выше это будет:
Conclusion:
A => B.
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1

def conclusion (set, relation):

"""
Conclusion
"""

conl_set =

for i in relation:

l =

for j in relation[i]:

v_set = set .value(i)

v_impl = relation[i][j]

l.append(t_norm(v_set, v_impl))

value = max (l)

conl_set.append((i, value))

return conl_set

Результат:
B" = {(x1, 1.0), (x2, 0.7), (x3, 1.0), (x4, 0.7)}.

Источники

Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. - М.: Горячая линия - Телеком, 2006. - 452 с.: ил.
Zadeh L. A. Fuzzy Sets, Information and Control, 1965, vol. 8, s. 338-353

– рассуждение, в котором осуществляется переход по правилам от высказывания или системы высказываний к высказыванию или системе высказываний. К логическому выводу обычно предъявляются (совместно или по отдельности) следующие требования: 1) правила перехода должны воспроизводить отношение "следования логического" (ту или иную его разновидность); 2) переходы в логическом выводе должны осуществляться на основе учета только синтаксических характеристик высказываний или систем высказываний.
В современной логике понятие логического вывода определяется для формальных систем, в которых высказывания представлены формулами. Обычно выделяют три основных типа формальных систем: аксиоматические исчисления, исчисления натурального вывода, исчисления секвенций. Стандартное определение логического вывода (из множества формул Г) для аксиоматического исчисления S таково: логический вывод в S из множества формул Г есть такая последовательность Α 1 ... А n формул языка исчисления S , что для каждой A i (1 ≤i ≤n) выполняется, по крайней мере, одно из следующих трех условий: 1) A i есть формула из Г; 2) A i есть аксиома исчисления S ; 3) A i есть формула, получающаяся из предшествующей ей в последовательности А 1 ...А n формулы или из предшествующих ей в этой последовательности формул по одному из правил вывода исчисления S. Если α есть логический вывод в S из множества формул Г, то формулы из Г называются посылками a, a сам вывод α называется выводом в S из посылок Г; если при этом А есть последняя формула α, то α называется логическим выводом в S формулы А из посылок Г.Запись «Г ⊦ s A» означает, что существует логический вывод в S формулы А из посылок Г. Логический вывод в S из пустого множества формул называется доказательством в S. Запись «⊦ s A» означает, что существует доказательство в S формулы А. Формула А называется доказуемой в S , если ⊦A. В качестве примера рассмотрим аксиоматическое исчисление S 1 со стандартным определением вывода, являющееся вариантом классической "логики высказываний" . Алфавит этого исчисления содержит только пропозициональные переменные р 1 , р 2 , ... , р n , ..., логические связки ⊃, ⌉ и круглые скобки. Определение формулы в этом языке обычное. Аксиомы S 1 – это формулы следующих шести видов (и только эти формулы):
I. (A ⊃A ),
II. ((A ⊃B )⊃((B ⊃C )⊃(A ⊃C ))),
III. ((A ⊃(B ⊃С ))⊃(B ⊃(A ⊃С ))),
IV. (A ⊃(⌉B ))⊃(B ⊃(⌉A ))),
V. ((⌉(⌉A)⊃А ),
VI. (((A ⊃B )⊃A )⊃A ).
Единственное правило исчисления S 1 модус поненс: А ⊃B ⊦B.
Определение логического вывода для S 1 является очевидной конкретизацией определения, данного выше. Следующая последовательность формул Ф1– Ф6 является логическим выводом в S 1 формулы ((p 1 ⊃p 2) ⊃р 2) из посылок {p 1).
Ф1. ((p 1 ⊃p 2) ⊃(p 1 ⊃p 2),
Ф2. (((p 1 ⊃p 2) ⊃(p 1 ⊃p 2)) ⊃(p 1 ⊃((p 1 ⊃p 2) ⊃p 2))),
Ф3. (p 1 ⊃((p 1 ⊃p 2) ⊃p 2)),
Ф4. p 1 ,
Ф5. ((p 1 ⊃p 2) ⊃p 2).
Анализ: Ф1 есть аксиома вида 1, Ф2 есть аксиома вида III, ФЗ получена по правилу модус поненс из Ф1 и Ф2, Ф4 есть посылка, Ф5 получена по правилу модус поненс из Ф4 и ФЗ. Итак, {p 1 }⊦ s1 ((p 1 ⊃p 2) ⊃p 2). Рассмотрев последовательность формул Φ1, Φ2 Ф3, убеждаемся, что ⊦ s1 (p 1 ⊃p 2) ⊃p 2)).
В ряде случаев логический вывод определяется так, что на использование некоторых правил накладываются ограничения. Напр., в аксиоматических исчислениях, являющихся вариантами классической "логики предикатов" первого порядка и содержащих среди правил вывода только модус поненс и правило обобщения, логический вывод часто определяется так, что на использование правила обобщения накладывается ограничение: любое применение правилам обобщения в α таково, что переменная, по которой проводится обобщение в этом применении правила обобщения, не входит ни в одну посылку, предшествующую в α нижней формуле этого применения правила обобщения. Цель этого ограничения обеспечить ряд полезных с точки зрения логики свойств вывода (напр., выполнение для простых форм "дедукции теоремы" ). Существуют определения логического вывода (как для аксиоматических, так и для исчислений других типов), которые (1) задают логический вывод не только из множества посылок, но допускают другие формы организации посылок (напр., списки или последовательности), (2) структурируют вывод не только линейно, но, напр., в форме дерева, (3) имеют явно выраженный индуктивный характер; при этом индуктивное определение вывода может вестись как по одной переменной (напр., по длине вывода), так и по нескольким переменным (напр., по длине логического вывода и по числу его посылок), (4) содержат формализацию зависимости между формулами в логическом выводе, и многие другие определения логического вывода, обусловленные иными способами формализации и аксиоматизации классических и неклассических систем логики. О некоторых из них см. в ст.

Энциклопедия эпистемологии и философии науки

вывод логический

ВЫВОД ЛОГИЧЕСКИЙ -рассуждение, в котором по определенным правилам осуществляется переход от высказываний или системы высказываний к высказыванию или системе высказываний. К В. л. обычно предъявляются (разом или по отдельности) следующие требования: 1) правила перехода должны воспроизводить отношение логического следования (ту или иную его разновидность), 2) переходы в В. л. должны осуществляться на основе учета только синтаксических характеристик высказываний или систем высказываний.

В современной логике В. л. определяется для формальных систем, в которых высказывания представлены формулами. Обычно выделяют три основных типа формальных систем: аксиоматические исчисления, исчисления натурального вывода, исчисления секвенций.

Стандартное определение В. л. (из множества формул Г) для аксиоматического исчисления S таково: В. л. в S из множества формул Г есть такая последовательность А г..А п формул языка исчисления S, что для каждой А. (1 < i < п) выполняется, по крайней мере, одно из следующих трех условий: 1) А. есть формула из Г; 2) А. есть аксиома исчисления S; 3) А. есть формула, получающаяся из предшествующей ей в последовательности А,... А формулы или из предшествующих ей в этой последовательности формул по правилу вывода исчисления S. Если а есть В. л. в S из множества формул Г, то формулы из Г называются посылками а, а сам вывод называется В. л. в S из посылок Г; если при этом А есть последняя формула а, то а называется В. л. в S формулы А из посылок Г. Запись «Г |- А» означает, что существует В. л. в S формулы А из посылок Г. В. л. в S из пустого множества формул называется доказательством в S. Запись «|- А» означает, что существует доказательство в S формулы А. Формула А называется доказуемой в S, если ч А. В качестве примера рассмотрим аксиоматическое исчисление S со стандартным определением вывода, являющееся вариантом аксиоматизации классической логики высказываний. Алфавит языка L этого исчисления содержит только пропозициональные переменные р, р 2 ,..., Р п > - - - > логические связки з, -> и круглые скобки. Определение L-формулы (формулы в языке L) обычное:

1) пропозициональная переменная есть L-формула,

2) если А и В есть L-формулы, то (А з В), (- > А) есть L-формулы,

3) ничто другое не есть L-формула. Аксиомы Sj - это все L-формулы следующих шести

видов (и только этих видов):

II ((ADB)D((BDC)3(ADC))),

III ((AD(BDQ)D(BD(ADC))),

IV ((ADhB))D(BDhA))),

VI (((A s > В) з A) з A). Единственное правило исчисления Sj есть правило

модус поненс в L: А, (А о В) / В (где А и В есть L-формулы).

Определение В. л. для S является очевидной конкретизацией стандартного определения В. л., которое дано выше.

Последовательность ((р 1 з р 2) з (р, з р 2)), (((р, з р 2) з

(Р, => Р 2 » 3 (Р, => ((Р, э Р 2) э Р 2)))> (P i 3 ((Р, 3 Р 2) 3 Р 2)) > Pi" ((р, з р 2) з р 2) L-формул является В. л. в S, L-формулы ((р; з р 2) з р 2) из pj. Действительно, первый член этой последовательности есть аксиома вида I, второй член этой последовательности есть аксиома вида III, третий член этой последовательности получается из первого и второго членов этой последовательности по правилу модус поненс в L, четвертый член этой последовательности есть L-формула из, пятый член этой последовательности получается из четвертого и третьего членов этой последовательности по правилу модус поненс в L. Итак, р, (- 51 ((р,зр 2)зр 2).

В ряде случаев В. л. определяется так, что использование в нем некоторых правил ограничивается. Напр., для некоторых аксиоматических исчислений, являющихся вариантами аксиоматизации классической логики предикатов первого порядка и содержащих среди правил вывода правило обобщения, В. л. иногда определяется так, что на использование правила обобщения накладывается ограничение, запрещающее применение в В. л. правила обобщения по переменной, входящей хотя бы в одну посылку данного В. л.

Известны В. л. (как для аксиоматических исчислений, так и для исчислений других типов) не только из множеств формул, но и из других систем формул (напр., из последовательностей формул, из списков формул). Исследуются В. л., не имеющие линейной структуры (любой В. л., удовлетворяющий стандартному определению В. л., имеет линейную структуру, ибо является последовательностью формул), а имеющие, напр., древовидную структуру. Рассматриваются В. л., содержащие формализацию зависимостей между входящими в них формулами, и многие другие В. л. Наличие большого числа разновидностей В. л. обусловлено как множественностью логик, так и многообразием задач, решаемых при их формализации.

- логический - формальный вывод в исчислении, содержащем логические правила и имеющем в качестве основных выводимых объектов формулы...
Математическая энциклопедия
- формальный вывод, по возмвжности приближенный к содержательному рассуждению, привычному для математика и логика...
Математическая энциклопедия
- в древнерусском зодчестве крепостное сооружение, выступающее перед основным. * * * 1. Форт. 2. Печная труба...
Архитектурный словарь
- в логике - рассуждение, в ходе которого из некоторых исходных высказываний, называемых посылками, с помощью логических правил получают новое высказывание, называемое заключением...
Философская энциклопедия
- ВЫВОД ЛОГИЧЕСКИЙ -рассуждение, в котором по определенным правилам осуществляется переход от высказываний или системы высказываний к высказыванию или системе высказываний...
Энциклопедия эпистемологии и философии науки
- рассуждение, в ходе которого из к.-л. исходных суждений - посылок - с помощью логических правил получают заключение - новое суждение...
Словарь логики
- англ. conclusion/deduction; нем. Schlussfolgerung. Умозаключение, в ходе к-рого из к.-л. исходных суждений получается логически вытекающее суждение. см. АБДУКЦИЯ, ДЕДУКЦИЯ, ИНДУКЦИЯ...
Энциклопедия социологии
- English: Terminal Часть электротехнического изделия, предназначенная для электрического соединения его с другими изделиями Источник: Термины и определения в электроэнергетике...
Строительный словарь
- 1. Термин, связанный с переводом информации, содержащейся в основном запоминающем устройстве компьютера, в поддерживающее запоминающее устройство...
Словарь бизнес терминов
- или умозаключение - процесс мысли, которым мы убеждаемся в истинности известного суждения при посредстве других суждений...
Энциклопедический словарь Брокгауза и Евфрона
- в логике, рассуждение, в ходе которого из каких-либо исходных суждений), посылок или предпосылок В., получается суждение, логически вытекающее из посылок. См. Дедукция, Индукция...
Большая Советская энциклопедия
- переход от посылок к следствиям по правилам логики...
Большой энциклопедический словарь
- ВЫ́ВОД, -а, муж. 1. см. вывести 1. 2. Умозаключение, то, что выведено. Важный в. Сделать необходимые выводы. 3. Провод, устройство, выходящее или выводящее что-н. наружу. | прил. выводной, -ая, -ое...
Толковый словарь Ожегова
- вы́вод сущ., м., употр. часто Морфология: чего? вы́вода, чему? вы́воду, что? вы́вод, чем? вы́водом, о чём? о вы́воде; мн. что? вы́воды, чего? вы́водов, чему? вы́водам, что? вы́воды, чем? вы́водами, о чём? о вы́водах 1...
Толковый словарь Дмитриева
- см....
Сводная энциклопедия афоризмов
- Дать вывод. Сиб. Ответить кому-л. ФСС, 53; СРНГ 7, 257. Сделать вывод. Кар. . Обменяться подарками. СРГК 1, 254...
Большой словарь русских поговорок

"вывод логический" в книгах

5.4. Логический анализ

Из книги Восстановление бухгалтерского учета, или Как «реанимировать» фирму автора Уткина Светлана Анатольевна

5.4. Логический анализ Во избежание ошибок и неточностей при составлении формы № 1 «Бухгалтерский баланс» целесообразно проанализировать по Главной книге обороты и остатки по счетам. Сделать это довольно просто. Рассмотрим на примере. К примеру, вы составляете

Логический позитивизм

Из книги Тень и реальность автора Свами Сухотра

Логический позитивизм Течение, возникшее в XX в. как развитие эмпиризма и позитивизма. Его сутью является теория верификации, утверждающая, что единственно валидной истиной является то, что подтверждено современными научными методами. Чтобы выразить эту истину, язык

2.9. Логический квадрат

Из книги Логика. Учебное пособие автора Гусев Дмитрий Алексеевич

2.9. Логический квадрат Отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата, который был разработан еще средневековыми логиками. Как видим, вершины квадрата обозначают четыре вида простых суждений, а его стороны и

2. Логический позитивизм

Из книги Введение в философию автора Фролов Иван

2. Логический позитивизм В 1922 году на кафедре натуральной философии Венского университета, которую после смерти Э. Маха возглавил профессор М. Шлик, собралась группа молодых ученых, поставивших перед собой смелую цель - реформировать науку и философию. Эта группа вошла

2. Логический обвал

Из книги Философия. Книга третья. Метафизика автора Ясперс Карл Теодор

2. Логический обвал - То, что может быть продемонстрировано или что требуется доказать, есть конечное познание чего-то особенного. Экзистенция и трансценденция, в смысле этого бытия, не существуют. Если мы мыслим о них, то мысль принимает логические формы, которые

Логический позитивизм

Из книги История философии автора Скирбекк Гуннар

Логический позитивизм В период между первой и второй мировыми войнами были выдвинуты новые философские идеи. Многие из них были стимулированы развитием неклассической физики и стали предметом серьезного эпистемологического анализа со стороны логического позитивизма.

Логический крючок

Из книги Виктор Суворов врет! [Потопить «Ледокол»] автора Верхотуров Дмитрий Николаевич

Логический крючок В использовании этой «концепции» у Виктора Суворова есть занятный момент. Подробно и многословно «доказывается» только второй тезис, тогда как остальные тезисы только упоминаются, очень кратко и без обоснования. Все внимание сосредоточивается на его

1.1. Наш логический вывод и свидетельство Ливия

Из книги автора

1.1. Наш логический вывод и свидетельство Ливия Прежде чем обратиться к первоисточникам, вспомним эмпирико-статистические и астрономические результаты, отождествляющие Царский Рим со Второй и Третьей Римскими империями, а также с Великой = «Монгольской» Империей XIII–XVI

Логический закон

БСЭ

Логический позитивизм

Из книги Большая Советская Энциклопедия (ЛО) автора БСЭ

Логический элемент

Из книги Большая Советская Энциклопедия (ЛО) автора БСЭ

Логический контекст

Из книги Firebird РУКОВОДСТВО РАЗРАБОТЧИКА БАЗ ДАННЫХ автора Борри Хелен

Логический контекст Простой способ рассматривать транзакцию между START TRANSACTION и COMMIT или ROLLBACK - это смотреть на нее как на серию клиентских операций и взаимодействий клиента и сервера, которые точно отображают задачу. Это очень полезная модель для понимания того, как

Логический тип

Из книги Описание языка PascalABC.NET автора Коллектив РуБоард

Логический тип Значения логического типа boolean занимают 1 байт и принимают одно из двух значений, задаваемых предопределенными константами True (истина) и False (ложь).Для логического типа определены статические методы: boolean.Parse(s) - функция, конвертирующая строковое

26. Логический анализ

Из книги Упражнения в стиле автора Кено Раймон

26. Логический анализ Автобус.Площадка.Площадка автобуса. Это место.Полдень.Приблизительно.Приблизительно полдень. Это время.Пассажиры.Ссора.Ссора пассажиров. Это действие.Молодой человек.Шляпа. Длинная тощая шея.Молодой человек в шляпе с плетенной тесьмой вокруг. Это

Логический способ

Из книги Активные продажи 3.1: Начало автора Рысев Николай Юрьевич

Логический способ Каждое возражение можно логически отразить – представить аргументы, достойные интеллекта клиента, и перевернуть его воззрения.К: У вас слишком молодая аудитория.П: Молодость – это стремительность, желание, деньги, решительность. Как вы смотрите на