Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?
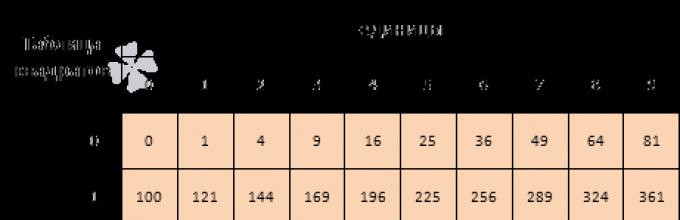
Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n
-ой степени из числа a
, при этом число a
содержится в таблице n
-ых степеней. По этой таблице находим число b
такое, что a=b n
. Тогда 
, следовательно, число b
будет искомым корнем n
-ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683
. Находим число 19 683
в таблице кубов, из нее находим, что это число является кубом числа 27
, следовательно, 
.
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3
. На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2
. Следовательно, 
.
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243
имеет вид 243=3 5
. Таким образом, 
.
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5
, а квадратный корень из знаменателя равен 13
. Тогда 
. На этом извлечение корня из обыкновенной дроби 25/169
завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000
. Тогда 
. Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13=
(2·3·13) 3 =78 3
и 1 000=10 3
, то 
и 
. Осталось лишь завершить вычисления 
.
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо 
. Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел
: чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: 
. Теперь смешанное число заменим обыкновенной дробью: 
. Применяем правило извлечения корня из обыкновенной дроби: 
. Осталось вычислить корни в числителе и знаменателе полученной дроби: 
.
Приведем краткую запись решения: 
.
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =0<5 , 10 2 =100>5 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 <5
, а 2 3 >5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 <5
, а 2,3 2 >5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =0<2 151,186 , 10 3 =1 000<2151,186 , 100 3 =1 000 000>2 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 <2 151,186
, а 20 3 >2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: 
.
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 - 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Рассмотрим сначала секущую АС, проведенную из внешней по отношению к данной окружности точки А (рис. 288). Из той же точки проведем касательную АТ. Будем называть отрезок между точкой А и ближайшей к ней точкой пересечения с окружностью внешней частью секущей (отрезок АВ на рис. 288), отрезок же АС до более далекой из двух точек пересечения - просто секущей. Отрезок касательной от А до точки касания также коротко называем касательной. Тогда справедлива
Теорема. Произведение секущей на ее внешнюю часть равно квадрату касательной.
Доказательство. Соединим точку . Треугольники ACT и ВТ А подобны, так как угол при вершине А у них общий, а углы ACT и равны, поскольку оба они измеряются половиной одной и той же дуги ТВ. Следовательно, Отсюда получаем требуемый результат:
Касательная равна среднему геометрическому между секущей, проведенной из той же точки, и ее внешней частью.
Следствие. Для любой секущей, проведенной через данную точку А, произведение ее длины на внешнюю часть постоянно:
Рассмотрим теперь хорды, пересекающиеся во внутренней точке. Справедливо утверждение:
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой (имеются в виду отрезки, на которые хорда разбивается точкой пересечения).
Так, на рис. 289 хорды АВ и CD пересекаются в точке М, и мы имеем Иначе говоря,
Для данной точки М произведение отрезков, на которые она разбивает любую проходящую через нее хорду, постоянно.
Для доказательства заметим, что треугольники МВС и MAD подобны: углы СМВ и DMA вертикальные, углы MAD и МСВ опираются на одну и ту же дугу. Отсюда находим
что и требовалось доказать.
Если данная точка М лежит на расстоянии l от центра, то, проведя через нее диаметр и рассматривая его как одну из хорд, найдем, что произведение отрезков диаметра, а значит, и любой другой хорды, равно Оно же равно квадрату минимальной полухорды (перпендикулярной к указанному диаметру), проходящей через М.
Теорема о постоянстве произведения отрезков хорды и теорема о постоянстве произведения секущей на ее внешнюю часть суть два случая одного и того же утверждения, различие состоит лишь в том, проводятся ли секущие через внешнюю или внутреннюю точку круга. Теперь можно указать еще один признак, отличающий вписанные четырехугольники:
Во всяком вписанном четырехугольнике произведения отрезное, на которые разбиваются диагонали точкой их пересечения, равны.
Необходимость условия очевидна, так как диагонали будут хордами описанной окружности. Можно показать, что это условие также и достаточно.
Теорема 111 . 1) Перпендикуляр, опущенный из какой-нибудь точки окружности на диаметр, среднепропорционален между частями диаметра. Этот перпендикуляр называется иногда ординатой.
2) Хорда, соединяющая конец диаметра с точкой окружности, среднепропорциональна между диаметром и отрезком, прилежащем хорде.
Дано. Опустим из какой-нибудь точки C окружности перпендикуляр CD на диаметр AB (черт. 169).
Требуется доказать, что 1) AD/CD = CD/DB, а также 2) AD/AC = AC/AB.
Доказательство . Соединим точку C с концами диаметра AB, тогда при точке C образуется прямой угол ACB, в котором отрезок CD есть перпендикуляр, опущенный из вершины прямого угла на гипотенузу.
На основании теоремы 100 имеет место пропорция:
на основании теоремы 101 пропорция:
AD/AC = AC/AB, DB/CB = CB/AB (1)
Следствие . Квадраты хорд относятся как соответствующие отрезки диаметра.
Доказательство . Из пропорции (1) следуют равенства:
AC 2 = AB · AD, CB 2 = AB · BD
откуда по разделении находим:
AC 2 /CB 2 = AD/DB.
Теорема 112 . Части пересекающихся хорд обратно пропорциональны между собой.
Даны две пересекающиеся хорды AB и CD (черт. 170).
Требуется доказать, что
т. е. большая часть первой хорды относится к большей части второй как меньшая часть второй хорды к меньшей части первой .
Доказательство . Соединим точку A с C и B с D, тогда образуются два подобных треугольника ACE и DBE, ибо углы при точке E равны как вертикальные, ∠CAB = ∠CDB как опирающиеся на концы дуги CB, ∠ACD = ∠ABD как опирающиеся на концы дуги AD.
Из подобия треугольников ACE и DBE вытекает пропорция:
BE/DE = CE/AE (a)
Из пропорции (a) вытекает равенство:
BE · AE = DE · CE
показывающее, что произведение отрезков одной равно произведению отрезков другой хорды.
Теорема 113 . Две секущие, проведенные из одной и той же точки вне окружности, обратно пропорциональны внешним своим частям.
Даны две секущие AB и AC, проведенные из точки A (черт 171).
Требуется доказать, что
т. е. первая секущая относится ко второй, как внешняя часть второй относится к внешней части первой секущей.
Доказательство . Соединим точки D с C, а B с E.
Два треугольника ∠ABE и ∠ADC подобны, ибо угол A общий, B = C как опирающиеся на концы одной и той же дуги DE, следовательно и ∠ADC = ∠AEB.
Из подобия треугольников ADC и ABE вытекает пропорция:
AC/AB = AD/AE (ЧТД).
Из этой же пропорции вытекает равенство
AC · AE = AB · AD
показывающее, что произведение секущей на ее внешний отрезок равно произведению другой секущей на ее отрезок (если секущие выходят из одной точки).
Теорема 114 . Касательная среднепропорциональна между целой секущей и внешней ее частью.
Дана касательная AB и секущая BC (черт. 172).
Требуется доказать, что
Доказательство . Соединим точку A с точками C и D.
Треугольники ABC и ABD подобны, ибо угол B общий, ∠BAD = ∠ACD, следовательно, ∠CAB = ∠ADB.
BC/AB = AB/BD (ЧТД).
Из этой пропорции вытекает равенство:
AB 2 = BC · BD
показывающее, что квадрат касательной равен произведению секущей на внешнюю ее часть .
Свойство сторон вписанного четырехугольника
Теорема 115 . Во всяком четырехугольнике, вписанном в круг, произведение диагоналей равно сумме произведений противоположных сторон.
Это предположение, известное под именем теоремы Птоломея, встречается в первый раз в сочинении Птоломея «Альагест» во II веке по Р. Х.
Дан вписанный четырехугольник ABCD (черт. 173) и проведены диагонали AC и BD.
Требуется доказать, что AC · BD = AB · CD + BC · AD.
Доказательство . Проведем прямую BE так, чтобы угол EBC равнялся углу ABD. Два треугольника ABD и BEC подобны, ибо ∠ABD = ∠CBE по построению, ∠ADB = ∠BCE как опирающиеся на одну и ту же дугу AB, следовательно,
Из подобия этих треугольников вытекает пропорция:
BC/BD = EC/AD (a)
Треугольники ABE и BCD подобны, ибо ∠ABE = ∠DBC по построению, ∠BAE = ∠BDC как опирающиеся на дугу BC, следовательно,
∠BEA = ∠BCD.
Из подобия этих треугольников вытекает пропорция:
AB/BD = AE/CD (b)
Из пропорций (a) и (b) вытекают равенства:
BC ·
AD = BD ·
EC
AB ·
CD = BD ·
AE
Сложив эти равенства, имеем:
BC · AD + AB · CD = BD · EC + BD · AE = BD (EC + AE)
Так как EC + AE = AC, то
BD · AC = BC · AD + AB · CD (ЧТД).
Теорема 116 . Во всяком вписанном четырехугольнике диагонали относятся как суммы произведений сторон, опирающихся на концы диагоналей.
Дан вписанный четырехугольник ABCD (черт. 174) и проведены диагонали AC и BD.
Требуется доказать, что
BD/AC = (AD · DC + AB · BC) / (BC · CD + AD · AB)
Доказательство . а) От точки B отложим дугу BE равную DC и соединим точку E с точками A, B, D.
Для вписанного четырехугольника ABED имеет место равенство:
AE · BD = AD · BE + AB · DE.
Так как BE = CD по построению, DE = BC, ибо ◡DE = ◡DC + ◡CE и ◡BC = ◡BE + ◡CE.
Заменив BE и DE их величинами, имеем равенство:
AE · BD = AD · CD + AB · BC (a)
b) Отложив от точки A дугу AF равную дуге BC и соединив точку F с точками A, D, C, имеем для четырехугольника AFCD равенство:
AC · DF = AF · CD + AD · CF
В этом равенстве AF = BC по построению, CF = AB (ибо ◡CF = ◡BC + ◡BF и ◡AB = ◡AF + ◡BF = ◡BC + ◡BF)
Заменяя величины AF и CF их величинами, найдем равенство:
AC · DF = BC · CD + AD · AB (b)
В равенствах (a) и (b) отрезки AE и DF равны, ибо
◡ADE = AD + DE = ◡AD + ◡BC = ◡AD + ◡AF = ◡DAF
Разделяя равенства (a) и (b), находим:
BC/AD = (AD · C D + AB · BC) / (BC · CD + AD · AB) (ЧТД).
Треугольник ABC – прямоугольный (рис. 11), C = 90°, СD перпендикулярна АВ, ВD и DА – проекции катетов ВС и АС на гипотенузу АВ. Теоремы: 1) высота, проведенная из вершины прямого угла на гипотенузу, есть средняя пропорциональная величина между проекциями катетов на гипотенузу, т.е. ; 2) каждый катет – средняя пропорциональная величина между гипотенузой и проекцией этого катета на гипотенузу, т. е. , .
Теорема Пифагора. Квадрат гипотенузы равен сумме квадратов катетов.
|
|
Теорема. Если через точку, взятую внутри
круга, проведены диаметр и произвольная хорда,
то произведение длин отрезков диаметра рав-
но произведению длин отрезков хорды, т.е. (рис. 12).
|
Следствие. Произведения длин отрезков пересекающихся хорд равны, т.е.
Теорема. Если из точки вне круга проведены касательная и се-кущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной, т.е. (рис. 13).
|
Определения. Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего этому углу катета к гипотенузе, косинусом – отношение прилежащего катета к гипотенузе, тангенсом отношение противолежащего катета к прилежащему, котангенсом – отношение прилежащего катета к противолежащему.
Из точки А вне окружности проведены касательная и секущая. Расстояние от А до точки касания 16 см, а от А до одной из точек пересечения секущей с окружностью 32 см. Найдите радиус окружности, если секущая удалена от ее центра на 5 см.
|
На рис. 14 АВ – касательная к окружности с центром O, AD – се-кущая. OK перпендикулярна DC, АВ = 16 см, АD = 32 см, OК = 5 см. По теореме о касательной и секущей или , АС = 8 см. см. По теореме о хордах, пересекающихся внутри круга, , но DK = KC, так как EP – диаметр, перпендикулярный хорде DС. Получим . Заменим в этом равенстве ЕК на , КР на , DК на 12, получим: OE = 13 см – искомый радиус.
104. Стороны прямоугольника 30 и 40 см. Найдите расстояние
от вершины прямоугольника до диагонали, не проходящей через эту вершину.
105. Периметр ромба равен 1 м. Одна диагональ длиннее другой на
1 дм. Вычислите диагонали ромба.
В круге по разные стороны от центра проведены параллельные хорды длиной 36 и 48 мм, расстояние между ними 42 мм. Вычислите радиус круга.
Катеты прямоугольного треугольника относятся как 5: 6, гипотенуза 122 см. Найдите отрезки гипотенузы, отсекаемые высотой.
Касательная и секущая, проведенные из одной точки к окружности, взаимно перпендикулярны. Касательная равна 12, внутренняя часть секущей равна 10. Найдите радиус окружности.
К окружности с радиусом 7 см проведены две касательные из одной точки, удаленной от центра на 25 см. Найдите расстояние между точками касания.
Ширина кольца, образованного двумя концентрическими окружностями, равна 8 дм, хорда большей окружности, касательная к меньшей, равна 4 м. Найдите радиусы окружностей.
Радиус окружности 7 см. Из точки, удаленной от центра на
9 см, проведена секущая так, что она делится окружностью на равные части. Найдите длину этой секущей.
Касательная к окружности равна 20 см, а наибольшая секущая, проведенная из той же точки, равна 50 см. Найдите радиус.
Из одной точки к окружности проведены касательная и секущая, длина которой а, а её внутренний отрезок больше внешнего на длину касательной. Найдите длину касательной.
В круг радиусом R вписан равнобедренный треугольник, у которого сумма высоты и основания равна диаметру круга. Найдите высоту треугольника.
В равнобедренном треугольнике основание и боковая сторона равны соответственно 48 и 30 дм. Вычислите радиусы кругов, описанного и вписанного, и расстояние между их центрами.
