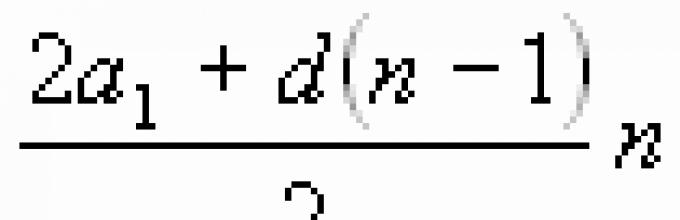- Обобщение и систематизация знаний учащихся по данной теме.
- Ознакомление учащихся с историческим материалом.
Оборудование: плакат к игре “Прогрессио – движение вперед”.
Все учащиеся разбиты на пять групп + совет мудрецов
Закончился двадцатый век.
Куда стремится человек?
Изучены космос и море,
Строенье звезд и вся Земля.
Но математиков зовет
Известный лозунг:
“Прогрессио – движение вперед”.
Сегодня у нас в классе состоится совет – совет Мудрецов. Мудрецы – ученики, сидящие в классе по группам. И Мудрецы, сидящие за этим столом.
Узнаёте ли вы их?
За столом сидят: Архимед, Гаусс, Магницкий.
Кто формулу суммы квадратов нашел?
И верной дорогой к прогрессу пришел?
Математик и физик. Я – Архимед.
О жизни моей ходит много легенд.
О! Я – Карл Гаусс! Нашел моментально сумму всех натуральных чисел от 1 до 100, будучи учеником начальной школы.
Магницкий. Господа! Имею честь представится. Я Леонтий Филиппович Магницкий – создатель первого учебника “Арифметика”.
Учитель. Скажите, ребята, почему эти ученые вдруг собрались вместе за одним столом? Какой вопрос математики объединяет их? Если вы не догодались, то внимательно посмотрите сценку.
Древняя индийская легенда
В классе появляется индусский царь со слугой.
Царь. Я, индусский царь Шерам, научился игре в шахматы и восхищен ее остроумием и разнообразием в ней положений. Слуга, позовим изобретателя Сету. Я желаю достойно наградить тебя, Сета, за прекрасную игру, которую ты придумал. Назови награду, которая тебя удовлетворит, и ты ее получишь.
Сета. Повелитель. Прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно
Царь. Простое пшеничное зерно?
Сета. Да, повелитель За вторую клетку прикажи выдать 2 зерна, за третью – 4, за четвертую – 8, за пятую – 16, и так до 64-й клетки.
Царь Шерам рассмеялся.
Учитель. О мудрецы 9– го класса, давайте посоветуемся. Стоит ли царю смеятся?
На доске запись: 1,2,4,8,16,….. S 64 – ?
Учащиеся решают. b 1= 1, q=2, n=64, S 64 =2 64 – 1.
Учитель. Как велико это число? Кто может это обяснить?
Архимед. Наимудрейшие! Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря, и океаны, и горы, и пустыню, и Арктику с Антарктидой, и получить удовлетворительный урожай, то, пожалуй, лет за пять он смог бы рассчитаться.
Гаусс. Математика – это точная наука. (Записывает на доске 18 446 744 073 709 551 615). 18 квинтильонов 446 квадрильонов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615.
Магницкий. Господа Мудрецы 9-го класса! Мои современники сказали бы так, что S 64 18,5 10 18 . Правда, я вам признаюсь, что в моем учебнике “Арифметика”, изданном 200 лет назад, по которому целых полвека учились дети, много задач по теме “Прогрессии”, но иные из них я сам решал с большим трудом, так как еще не нашел всех формул, связывающих входящие в них величины.
Под скрип пера о лист бумаги.
Заполните сии листы!
Да помогут вам наши начинанья!
Раздаются загатовки листов для проверки знаний теории, т. е. восстанавливается опорный конспект по теме “Прогрессии”.
Ученики заполняют таблицу. На доске появляется следующая таблица:
Прогрессии |
Арифметическая a n |
Геометрическая b n |
|
Определение |
b n+1 =b n q (q0,q1) |
||
Формула n первых членов |
a n =a 1 + (n-1)d |
||
Сумма n первых членов прогрессии |
S n = |
S n =
И поиск их был нами оценен. “Математика – царица наук, арифметика – царица математики”
|
Арифметическая и геометрическая прогрессии
Теоретические сведения
Теоретические сведения
Арифметическая прогрессия |
Геометрическая прогрессия |
|
Определение |
Арифметической прогрессией a n называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d (d - разность прогрессий) |
Геометрической прогрессией b n называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число q (q - знаменатель прогрессии) |
Рекуррентная формула |
Для любого натурального n
|
Для любого натурального n
|
Формула n-ого члена |
a n = a 1 + d (n – 1) |
b n = b 1 ∙ q n - 1 , b n ≠ 0 |
| Характеристическое свойство |  |
|
| Сумма n-первых членов |  |
 |
Примеры заданий с комментариями
Задание 1
В арифметической прогрессии (a n ) a 1 = -6, a 2
По формуле n-ого члена:
a 22 = a 1 + d (22 - 1) = a 1 + 21 d
По условию:
a 1 = -6, значит a 22 = -6 + 21 d .
Необходимо найти разность прогрессий:
d = a 2 – a 1 = -8 – (-6) = -2
a 22 = -6 + 21 ∙ (-2) = - 48.
Ответ : a 22 = -48.
Задание 2
Найдите пятый член геометрической прогрессии: -3; 6;....
1-й способ (с помощью формулы n -члена)
По формуле n-ого члена геометрической прогрессии:
b 5 = b 1 ∙ q 5 - 1 = b 1 ∙ q 4 .
Так как b 1 = -3,
2-й способ (с помощью рекуррентной формулы)
Так как знаменатель прогрессии равен -2 (q = -2), то:
b 3 = 6 ∙ (-2) = -12;
b 4 = -12 ∙ (-2) = 24;
b 5 = 24 ∙ (-2) = -48.
Ответ : b 5 = -48.
Задание 3
В арифметической прогрессии (a n ) a 74 = 34; a 76 = 156. Найдите семьдесят пятый член этой прогрессии.
Для арифметической прогрессии характеристическое свойство имеет вид ![]() .
.
Из этого следует:
![]() .
.
Подставим данные в формулу:
![]()
Ответ : 95.
Задание 4
В арифметической прогрессии (a n ) a n = 3n - 4. Найдите сумму семнадцати первых членов.
Для нахождения суммы n-первых членов арифметической прогрессии используют две формулы:
![]() .
.
Какую из них в данном случае удобнее применять?
По условию известна формула n-ого члена исходной прогрессии (a n ) a n = 3n - 4. Можно найти сразу и a 1 , и a 16 без нахождения d . Поэтому воспользуемся первой формулой.

Ответ : 368.
Задание 5
В арифметической прогрессии(a n ) a 1 = -6; a 2 = -8. Найдите двадцать второй член прогрессии.
По формуле n-ого члена:
a 22 = a 1 + d (22 – 1) = a 1 + 21d .
По условию, если a 1 = -6, то a 22 = -6 + 21d . Необходимо найти разность прогрессий:
d = a 2 – a 1 = -8 – (-6) = -2
a 22 = -6 + 21 ∙ (-2) = -48.
Ответ : a 22 = -48.
Задание 6
Записаны несколько последовательных членов геометрической прогрессии:
![]()
Найдите член прогрессии, обозначенный буквой x .
При решении воспользуемся формулой n-го члена b n = b 1 ∙ q n - 1 для геометрических прогрессий. Первый член прогрессии. Чтобы найти знаменатель прогрессии q необходимо взять любой из данных членов прогрессии и разделить на предыдущий. В нашем примере можно взять и разделить на. Получим, что q = 3. Вместо n в формулу подставим 3, так как необходимо найти третий член, заданной геометрической прогрессии.
Подставив найденные значения в формулу, получим:
![]() .
.
Ответ : .
Задание 7
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие a 27 > 9:
Так как заданное условие должно выполняться для 27-го члена прогрессии, подставим 27 вместо n в каждую из четырех прогрессий. В 4-й прогрессии получим:
![]() .
.
Ответ : 4.
Задание 8
В арифметической прогрессии a 1 = 3, d = -1,5. Укажите наибольшее значение n , для которого выполняется неравенство a n > -6.
Понятие числовой последовательности подразумевает соответствие каждому натуральному числу некоторого действительного значения. Такой ряд чисел может быть как произвольным, так и обладать определенными свойствами – прогрессия. В последнем случае каждый последующий элемент (член) последовательности можно вычислить с помощью предыдущего.
Арифметическая прогрессия – последовательность числовых значений, в которой ее соседние члены разнятся между собой на одинаковое число (подобным свойством обладают все элементы ряда, начиная со 2-ого). Данное число – разница между предыдущим и последующим членом – постоянно и называется разностью прогрессии.
Разность прогрессии: определение
Рассмотрим последовательность, состоящую из j значений A = a(1), a(2), a(3), a(4) … a(j), j принадлежит множеству натуральных чисел N. Арифметическая прогрессия, согласно своего определения, – последовательность, в которой a(3) – a(2) = a(4) – a(3) = a(5) – a(4) = … = a(j) – a(j-1) = d. Величина d – искомая разность данной прогрессии.
d = a(j) – a(j-1).
Выделяют:
- Возрастающую прогрессию, в таком случае d > 0. Пример: 4, 8, 12, 16, 20, …
- Убывающую прогрессию, тогда d < 0. Пример: 18, 13, 8, 3, -2, …
Разность прогрессии и ее произвольные элементы
Если известны 2 произвольных члена прогрессии (i-ый, k-ый), то установить разность для данной последовательности можно на базе соотношения:
a(i) = a(k) + (i – k)*d, значит d = (a(i) – a(k))/(i-k).
Разность прогрессии и ее первый член
Данное выражение поможет определить неизвестную величину лишь в случаях, когда известен номер элемента последовательности.
Разность прогрессии и ее сумма
Сумма прогрессии – это сумма ее членов. Для вычисления суммарного значения ее первых j элементов воспользуйтесь соответствующей формулой:
S(j) =((a(1) + a(j))/2)*j, но т.к. a(j) = a(1) + d(j – 1), то S(j) = ((a(1) + a(1) + d(j – 1))/2)*j=((2a(1) + d(– 1))/2)*j.