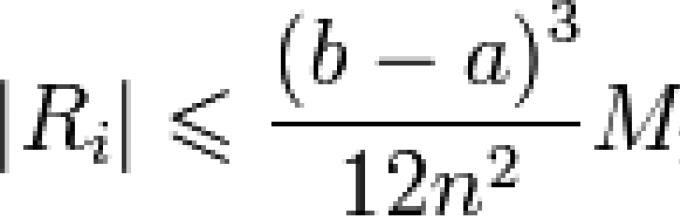Ранее мы рассматривали определенный интеграл как разность значений первообразной для подынтегральной функции. При этом предполагалось, что подынтегральная функция имеет первообразную на промежутке интегрирования.
В случае, когда первообразная выражается через элементарные функции, мы можем быть уверенными в ее существовании. Но если такого выражения нет, то вопрос о существовании первообразной остается открытым, и мы не знаем, существует ли соответствующий определенный интеграл.
Геометрические соображения подсказывают, что хотя, например, для функции y=e^{-x^2} нельзя выразить первообразную через элементарные функции, интеграл \textstyle{\int\limits_{a}^{b}e^{-x^2}\,dx} существует и равен площади фигуры, ограниченной осью абсцисс, графиком функции y=e^{-x^2} и прямыми x=a,~ x=b (рис. 6). Но при более строгом анализе выясняется, что само понятие площади нуждается в обосновании, а потому нельзя опираться на него, решая вопросы существования первообразной и определенного интеграла.
Докажем, что любая функция, непрерывная на отрезке имеет на этом отрезке первообразную , и, следовательно, для нее существует определенный интеграл по этому отрезку. Для этого нам понадобится иной подход к понятию определенного интеграла, не опирающийся на предположение о существовании первообразной.
Установим сначала некоторые свойства определенного интеграла , понимаемого как разность значений первообразной.
Оценки определенных интегралов
Теорема 1. Пусть функции y=f(x) ограничена на отрезке , а m=\min_{x\in}f(x) и M=\max_{x\in}f(x) , соответственно, наименьшее и наибольшее значения функции y=f(x) на , причем на этом отрезке функция y=f(x) имеет первообразную. Тогда
m(b-a)\leqslant \int\limits_{a}^{b}f(x)\,dx\leqslant M(b-a).
Доказательство. Пусть F(x) - одна из первообразных для функции y=f(x) на отрезке . Тогда
\int\limits_{a}^{b}f(x)\,dx=\Bigl.{F(x)}\Bigr|_{a}^{b}=F(b)-F(a).
По теореме Лагранжа F(b)-F(a)=F"(c)(b-a)
, где a
По условию для всех значений x из отрезка выполняется неравенство m\leqslant f(x)\leqslant M , поэтому m\leqslant f(c)\leqslant M и, следовательно,
m(b-a)\leqslant f(c)(b-a)\leqslant M(b-a) , то есть m(b-a)\leqslant \int\limits_{a}^{b}f(x)\,dx\leqslant M(b-a) ,
что и требовалось доказать.
Двойное неравенство (1) дает лишь весьма грубую оценку для значения определенного интеграла. Например, на отрезке значения функции y=x^2 заключены между 1 и 25, а потому имеют место неравенства
4=1\cdot(5-1)\leqslant \int\limits_{1}^{5}x^2\,dx\leqslant 25\cdot(5-1)=100.
Чтобы получить более точную оценку, разбивают отрезок
на несколько частей точками a=x_0
m_k\cdot\Delta x_k\leqslant \int\limits_{x_k}^{x_{k+1}} f(x)\,dx\leqslant M_k\cdot \Delta x_k\,
где через \Delta x_k обозначена разность (x_{k+1}-x_k) , т. е. длина отрезка . Записывая эти неравенства для всех значений k от 0 до n-1 и складывая их, получим:
\sum_{k=0}^{n-1}(m_k\cdot\Delta x_k) \leqslant \sum_{k=0}^{n-1} \int\limits_{x_k}^{x_{k+1}}f(x)\,dx\leqslant \sum_{k=0}^{n-1} (M_k\cdot \Delta x_k),
Но по аддитивному свойству определенного интеграла сумма интегралов по всем частям отрезка равна интегралу по этому отрезку, т. е.
\sum_{k=0}^{n-1} \int\limits_{x_k}^{x_{k+1}}f(x)\,dx= \int\limits_a}^{b}f(x)\,dx\,.
Значит,
\sum_{k=0}^{n-1}(m_k\cdot\Delta x_k) \leqslant \sum_{k=0}^{n-1} \int\limits_{a}^{b}f(x)\,dx\leqslant \sum_{k=0}^{n-1} (M_k\cdot \Delta x_k)
Например, если разбить отрезок на 10 равных частей, каждая из которых имеет длину 0,4, то на частичном отрезке выполняется неравенство
(1+0,\!4k)^2\leqslant x^2\leqslant \bigl(1+0,\!4(k+1)\bigr)^2
Поэтому имеем:
0,\!4\sum_{k=0}^{9}(1+0,\!4k)^2\leqslant \int\limits_{1}^{5}x^2\,dx\leqslant 0,\!4\sum_{k=0}^{9}\bigl(1+0,\!4(k+1)\bigr)^2.
Вычисляя, получаем: 36,\!64\leqslant \int\limits_{1}^{5} x^2\,dx\leqslant 46,\!24 . Эта оценка гораздо точнее полученной ранее 4\leqslant \int\limits_{1}^{5}x^2\,dx\leqslant100 .
Чтобы получить еще более точную оценку интеграла, надо разбить отрезок не на 10, а, скажем, на 100 или 1000 частей и сосчитать соответствующие суммы. Разумеется, данный интеграл проще вычислить с помощью первообразной:
\int\limits_{1}^{5}x^2\,dx= \left.{\frac{x^3}{3}}\right|_{1}^{5}= \frac{1}{3}(125-1)= \frac{124}{3}\,.
Но если выражение для первообразной нам неизвестно, то неравенства (2) дают возможность оценить значение интеграла снизу и сверху.
Определенный интеграл как разделяющее число
Числа m_k и M_k , входящие в неравенство (2), могли выбираться произвольно, лишь бы на каждом из отрезков выполнялось неравенство m_k\leqslant f(x)\leqslant M_k . Наиболее точная оценка интеграла при данном разбиении отрезка получится, если взять M_k наименьшим, а m_k наибольшим из всех возможных значений. Это значит, что в качестве m_k надо взять точную нижнюю границу значений функции y=f(x) на отрезке , а в качестве M_k - точную верхнюю границу этих значений на том же отрезке:
m_k=\inf_{x\in}f(x),\qquad M_k=\sup_{x\in}f(x).
Если y=f(x) - ограниченная функция на отрезке , то она ограничена и на каждом из отрезков , а потому для нее определены по равенствам (3) числа m_k и M_k,~ 0\leqslant k\leqslant n-1 . При таком выборе чисел m_k и M_k суммы \textstyle{\sum\limits_{k=0}^{n-1}m_k\Delta x_k} и \textstyle{\sum\limits_{k=0}^{n-1}M_k\Delta x_k} называют, соответственно, нижней и верхней интегральными суммами Дарбу для функции y=-f(x) при данном разбиении P:
a=x_0 отрезка
. Будем обозначать эти суммы соответственно s_{fP}
и S_{fP}
, а если функция y=f(x)
фиксирована, то просто s_P
и S_P
. Неравенство (2) означает, что если ограниченная на отрезке
функция y=f(x)
имеет на этом отрезке первообразную, то определенный интеграл разделяет числовые множества \{s_p\}
и \{S_P\}
, состоящие соответственно из всех нижних и верхних сумм Дарбу для всевозможных разбиений P
отрезка
. Вообще говоря, может случиться, что число, разделяющее эти два множества, не единственно. Но ниже мы увидим, что для наиболее важных классов функций (в частности, для непрерывных функций) оно единственно. Это позволяет ввести новое определение для \textstyle{\int\limits_{a}^{b} f(x)\,dx}
, не опирающееся на понятие первообразной, а использующее лишь суммы Дарбу. Определение.
Функция y=f(x)
, ограниченная на отрезке
, называется интегрируемой на этом отрезке, если существует единственное число \ell
, разделяющее множества нижних и верхних сумм Дарбу, образованных для всевозможных разбиений отрезка
. Если функция y=f(x)
интегрируема на отрезке
, то единственное число, разделяющее эти множества, называют определенным интегралом этой функции по отрезку
и означают . Мы определили интеграл \textstyle{\int\limits_{a}^{b} f(x)\,dx}
для случая, когда ab
, то положим \int\limits_{a}^{b}f(x)\,dx= -\int\limits_{b}^{a}f(x)\,dx\,.
Это определение естественно, так как при изменении направления промежутка интегрирования все разности \Delta x_k=x_{k+1}-x_k
меняют знак, а тогда меняют знаки и суммы Дарбу и, тем самым, разделяющее их число, т.е. интеграл. Так как при a=b
все \Delta x_k
обращаются в нуль, то положим \int\limits_{b}^{a}f(x)\,dx=0.
Мы получили два определения понятия определенного интеграла: как разности значений первообразной и как разделяющего числа для сумм Дарбу. Эти определения в наиболее важных случаях приводят к одному и тому же результату: Теорема 2.
Если функция y=f(x)
ограничена на отрезке
и имеет на нем первообразную y=F(x)
, причем существует единственное число, разделяющее нижние и верхние суммы Дарбу, то это число равно F(b)-F(a)
.
Доказательство.
Мы доказали выше, что число F(a)-F(b)
разделяет множества \{s_P\}
и \{S_P\}
. Так как по условию разделяющее число однозначно определено, то оно совпадает с F(b)-F(a)
. Начиная с этого момента мы будем применять обозначение \textstyle{\int\limits_{a}^{b}f(x)\,dx}
лишь для единственного числа, разделяющего множества \{s_P\}
и \{S_P\}
. Из доказанной теоремы следует, что при этом не возникает противоречия с тем пониманием этого обозначения, которым мы пользовались выше. Для того чтобы данное ранее определение интеграла имело смысл, надо доказать, что множество верхних сумм Дарбу действительно расположено справа от множества нижних сумм Дарбу. Лемма 1.
Для каждого разбиения P
соответствующая нижняя сумма Дарбу не превосходит верхней суммы Дарбу, s_P\leqslant S_P
.
Доказательство.
Рассмотрим некоторое разбиение P
отрезка
: a=x_0 Очевидно, что для любого k
и для любого выбранного разбиения P
выполняется неравенство s_P\leqslant S_P
. Следовательно, m_k\cdot\Delta x_k\leqslant M_k\cdot\Delta x_k
, и потому s_P= \sum_{k=0}^{n-1}(m_k\cdot\Delta x_k)\leqslant \sum_{k=0}^{n-1}(M_k\cdot\Delta x_k)=S_P.
Неравенство (4) справедливо лишь для фиксированного разбиения P
. Поэтому пока еще нельзя утверждать, что нижняя сумма Дарбу одного разбиения не может превзойти верхнюю сумму Дарбу другого разбиения. Для доказательства этого утверждения нам понадобится следующая лемма: Лемма 2.
От добавления новой точки деления нижняя сумма Дарбу не может уменьшиться, а верхняя сумма не может увеличиться.
Доказательство.
Выберем некоторое разбиение P
отрезка
и добавим к нему новую точку деления {x^{\ast}}
. Обозначим новое разбиение P^{\ast}
. Разбиение P^{\ast}
является измельчением разбиения P
, т.е. каждая точка разбиения P
является, одновременно и точкой разбиения P^{\ast}
. Пусть точка {x^{\ast}}
попала на отрезок \colon\, x_k Слагаемому m_k(x_{k+1}-m_{k})
первоначальной нижней суммы Дарбу в новой нижней сумме Дарбу соответствуют два слагаемых: m_{k}^{\ast}(x^{\ast}-x_k)+ m_{k}^{\ast\ast}(x_{k+1}-x^{\ast}).
При этом m_k\leqslant m_{k}^{\ast}
и m_k\leqslant m_{k}^{\ast\ast}
, так как m_k
- точная нижняя граница значений функции f(x)
на всем отрезке
, а m_{k}^{\ast}
и m_{k}^{\ast\ast}
лишь на его частях
и
соответственно. Оценим снизу сумму полученных слагаемых: \begin{aligned} m_{k}^{\ast}\bigl(x^{\ast}-x_{k}\bigr)+ m_{k}^{\ast\ast}\bigl(x_{k+1}-x^{\ast}\bigr) \geqslant & \,\,m_k \bigl(x^{\ast}-x_k)+m_k(x_{k+1}-x^{\ast}\bigr)=\\ &=m_k\bigl(x^{\ast}-x_k+x_{k+1}-x^{\ast}\bigr)=\\ &=m_k\bigl(x_{k+1}-x_k\bigr).\end{aligned}
Так как остальные слагаемые и в старой и в новой нижних суммах Дарбу остались неизменными, то нижняя сумма Дарбу от добавления новой точки деления не уменьшилась, s_P\leqslant S_P
. Доказанное утверждение остается справедливым и при добавлении любого конечного числа точек к разбиению P
. Аналогично доказывается утверждение о верхней сумме Дарбу: S_{P^{\ast}}\leqslant S_{P}
. Перейдем к сравнению сумм Дарбу для любых двух разбиений. Лемма 3.
Ни одна нижняя сумма Дарбу не превосходит любой верхней суммы Дарбу (хотя бы отвечающей другому разбиению отрезка
).
Доказательство.
Рассмотрим два произвольных разбиения P_1
и P_2
отрезка
и образуем третье разбиение P_3
, состоящее из всех точек разбиений P_1
и P_2
. Таким образом, разбиение P_3
является измельчением как разбиения P_1
, так и разбиения P_2
(рис. 7). Обозначим нижние и верхние суммы Дарбу для этих разбиений соответственно s_1,~S_1.~s_2,~S_2
и докажем, что s_1\leqslant S_2
. Так как P_3
- измельчение разбиения P_1
, то s_1\leqslant s_3
. Далее, s_3\leqslant S_3
, поскольку суммы s_3
и S_3
соответствуют одному и тому же разбиению. Наконец, S_3\leqslant S_2
, так как P_3
является измельчением разбиения P_2
. Таким образом, s_1\leqslant s_3\leqslant S_3\leqslant S_2
, т.е. s_1\leqslant S_2
, что и требовалось доказать. Из леммы 3 следует, что числовое множество X=\{s_P\}
нижних сумм Дарбу лежит левее числового множества Y=\{S_P\}
верхних сумм Дарбу.
В силу теоремы о существовании разделяющего числа для двух числовых множеств1, найдется хотя бы одно число /, разделяющее множества X
и Y
, т.е. такое, что для любого разбиения отрезка
выполняется двойное неравенство: s_P= \sum_{k=0}^{n-1}\bigl(m_k\cdot\Delta x_k\bigr) \leqslant I\leqslant \sum_{k=0}^{n-1}\bigl(M_k\cdot\Delta x_k\bigr)=S_P.
Если это число единственно, то \textstyle{I= \int\limits_{a}^{b} f(x)\,dx}
. Приведем пример, показывающий, что такое число I
, вообще говоря, не является однозначно определенным. Напомним, что функцией Дирихле называют функцию y=D(x)
на отрезке
, определяемую равенствами: D(x)= \begin{cases}0,& \text{if}~~ x~~\text{is irrational number};\\1,& \text{if}~~ x~~ \text{is rational number}.\end{cases}
Какой бы отрезок
мы ни взяли, на нем найдутся и рациональные, и иррациональные точки, т.е. и точки, где D(x)=0
, и точки, где D(x)=1
. Поэтому для любого разбиения отрезка
все значения m_k
равны нулю, а все значения M_k
равны единице. Но тогда все нижние суммы Дарбу \textstyle{\sum\limits_{k=0}^{n-1}\bigl(m_k\cdot\Delta x_k\bigr)}
равны нулю, а все верхние суммы Дарбу \textstyle{\sum\limits_{k=0}^{n-1}\bigl(M_k\cdot\Delta x_k\bigr)}
равны единице, Метод трапеций
Основная статья:
Метод трапеций
Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций. Площадь трапеции на каждом отрезке: Погрешность аппроксимации на каждом отрезке: Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины : Погрешность формулы трапеций: Метод Симпсона.
Рассмотрим два шага интегрирования (h
= const = x i+1 – x i
), то есть три узла x 0 , x 1 , x 2
, через которые проведем параболу, воспользовавшись уравнением Ньютона: Пусть z = x - x 0
, Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу: . Здесь [править]Увеличение точности
Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла. Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них. При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для аналитических функций для любого численного метода. Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге. Применение правила Рунге
править]Оценка точности вычисления определённого интеграла
Интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном 2n. Погрешность вычисления значения интеграла при числе шагов, равном 2n, определяется по формуле Рунге: Особенности поведения погрешности.
Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R
результатов численного расчета в зависимост Уточняющая формула Ромберга.
Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h
. Прикладное значение теоремы о среднем
заключается в возможности получения качественной оценки значения определенного интеграла без его вычисления. Формулируем
: если функция непрерывна на интервале , то внутри этого интервала найдется такая точка , что Эта формула вполне пригодна для прикидочной оценки интеграла от сложной или громоздкой функции. Единственным моментом, который делает формулу приближенной
, является необходимость самостоятельного выбора
точки . Если принять наиболее простой путь - середину интервала интегрирования (как предлагается в ряде учебников), то ошибка может быть весьма значительной. Для получения более точного результата рекомендуем
провести расчет в следующей последовательности: Построить график функции на интервале ; Провести верхнюю границу прямоугольника таким образом, чтобы отсекаемые части графика функции были примерно равны по площади
(именно так показано на вышеприведенном рисунке - два криволинейных треугольника практически одинаковы); Определить из рисунка ; Воспользоваться теоремой о среднем. В качестве примера вычислим простой интеграл : Точное значение ; Для середины интервала Построив график с проведением верхней стороны прямоугольника в соответствии с рекомендациями, получим , откуда и приближенное значение . Вполне удовлетворительный результат, погрешность составляет 0,75%. Точность расчетов с помощью теоремы о среднем существенно зависит, как было показано, от визуального назначения
по графику точки . Действительно, выбрав, в том же примере, точки или , можно получить другие значения интеграла, причем погрешность может и увеличиться. Субъективные факторы, масштаб графика и качество рисования сильно влияют на результат. Это неприемлемо
в ответственных расчетах, поэтому теорема о среднем применяется только для быстрой качественной
оценки интеграла. В этом разделе рассмотрим один из самых популярных способов приближенного интегрирования - формулу трапеций
. Основная идея построения этой формулы исходит из того, что кривую можно приближенно заменить ломаной линией, как показано на рисунке. Примем, для определенности (и в соответствии с рисунком), что интервал интегрирования разбит на равные
(это необязательно, но очень удобно) части. Длина каждой из этих частей вычисляется по формуле и называется шагом
. Абсциссы точек разбиения, если задано , определятся по формуле , где . По известным абсциссам легко вычислить ординаты . Таким образом, Это и есть формула трапеций для случая . Отметим, что первое слагаемое в скобках является полусуммой начальной и конечной ординат, к которой прибавляются все промежуточные ординаты. Для произвольного числа разбиений интервала интегрирования общая формула трапеций
имеет вид:квадратурных формул
: прямоугольников, Симпсона, Гаусса и т.д. Они строятся на той же идее представления криволинейной трапеции элементарными площадями различной формы, поэтому, после освоения формулы трапеций, разобраться в аналогичных формулах не составит особого труда. Многие формулы не так просты, как формула трапеций, но позволяют получить результат высокой точности при малом числе разбиений . С помощью формулы трапеций (или аналогичных) можно вычислять, с нужной на практике точностью, как "неберущиеся" интегралы, так и интегралы от сложных или громоздких функций. Определённым интегралом
от непрерывной функции f
(x
) на конечном отрезке [a
, b
] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом
(Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F
(b
) - F
(a
)). Числа a
и b
называются соответственно нижним и верхним пределами интегрирования, а отрезок [a
, b
] – отрезком интегрирования. Таким образом, если F
(x
) – какая-нибудь первообразная функция для f
(x
), то, согласно определению, Равенство (38) называется формулой Ньютона-Лейбница
. Разность F
(b
) – F
(a
) кратко записывают так: Поэтому формулу Ньютона-Лейбница будем записывать и так: Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F
(x
) и Ф(х
) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х
) = F
(x
) + C
. Поэтому Тем самым установлено, что на отрезке [a
, b
] приращения всех первообразных функции f
(x
) совпадают. Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная
С
из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела
b
, далее - значение
нижнего предела
a
и вычисляется разность
F(b) - F(a)
. Полученное число и будет
определённым интегралом.
. При a
= b
по определению принимается Пример 1.
Решение. Сначала найдём неопределённый интеграл: Применяя формулу Ньютона-Лейбница к первообразной (при С
= 0), получим Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39). Пример 2.
Вычислить определённый интеграл Решение. Используя формулу Теорема 2.
Величина определённого интеграла не зависит от обозначения переменной интегрирования
, т.е. Пусть F
(x
) – первообразная для f
(x
). Для f
(t
) первообразной служит та же функция F
(t
), в которой лишь иначе обозначена независимая переменная. Следовательно, На основании формулы (39) последнее равенство означает равенство интегралов Теорема 3.
Постоянный множитель можно выносить за знак определённого интеграла
, т.е. Теорема 4.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций
, т.е. Теорема 5.
Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям
, т.е. если Теорема 6.
При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак
, т.е. Теорема 7
(теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его
, т.е. Теорема 8.
Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9.
Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать
, т.е. Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов. Пример 5.
Вычислить определённый интеграл Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим Пусть f
(x
) – непрерывная на отрезке [a
, b
] функция, а F
(x
) – её первообразная. Рассмотрим определённый интеграл а через t
обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х
меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х
, которую обозначим через Ф
(х
), т.е. Докажем, что функция Ф
(х
) является первообразной для f
(x
) = f
(t
). Действительно, дифференцируя Ф
(х
), получим так как F
(x
) – первообразная для f
(x
), а F
(a
) – постояная величина. Функция Ф
(х
) – одна из бесконечного множества первообразных для f
(x
), а именно та, которая при x
= a
обращается в нуль. Это утверждение получается, если в равенстве (48) положить x
= a
и воспользоваться теоремой 1 предыдущего параграфа. где, по определению, F
(x
) – первообразная для f
(x
). Если в подынтегральном выражении произвести замену переменной то в соответствии с формулой (16) можно записать В этом выражении первообразная функция для В самом деле, её производная, согласно правилу дифференцирования сложной функции
, равна Пусть α и β – значения переменной t
, при которых функция принимает соответственно значения a
и b
, т.е. Но, согласно формуле Ньютона-Лейбница, разность F
(b
) – F
(a
) естьСвойства нижних и верхних сумм Дарбу
что и требовалось доказать.
![]() где
где ![]()
 где
где ![]() где
где ![]()
 Подынтегральная функция f(x)
заменяется интерполяционным полиномом второй степениP(x)
– параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).
Подынтегральная функция f(x)
заменяется интерполяционным полиномом второй степениP(x)
– параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).
тогда
Для равномерной сетки
и четного числа шагов n
формула Симпсона принимает вид:![]() , а
, а  в предположении непрерывности четвертой производной подынтегральной функции.
в предположении непрерывности четвертой производной подынтегральной функции.
, для формул прямоугольников и трапеций , а для формулы Симпсона .
Таким образом, интеграл вычисляется для последовательных значений числа шагов , где n 0 - начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения N будет выполнено условие , где ε - заданная точность. и от числа n
разбиений интервала (то есть при шаг . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R min
, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R
.
и от числа n
разбиений интервала (то есть при шаг . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R min
, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R
.
Обозначим интеграл с числом разбиений n
= 1 как ![]() .
.
Уменьшив шаг в два раза, получим ![]() .
.
Если последовательно уменьшать шаг в 2 n раз, получим рекуррентное соотношение для расчета . .
.
![]() получим и приближенное значение , т.е. явно неточный результат;
получим и приближенное значение , т.е. явно неточный результат;Формула трапеций


![]() (38)
(38)![]() (39)
(39)
![]()
![]()
![]()
Свойства определённого интеграла
![]() (40)
(40)![]()
![]() (41)
(41)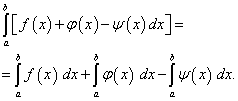 (42)
(42)![]() (43)
(43)![]() (44)
(44)![]() (45)
(45)
![]() (46)
(46)![]()

Определённый интеграл с переменным верхним пределом
![]() (47)
(47)![]() (48)
(48)
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
![]()