Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы - буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через
фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и директрисой (рис. 19). В этой системе координат данная парабола будет определяться уравнением
у 2 = 2рх. (1)
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
Фокальный радиус произвольной точки М(х; у) параболы (т. е. длина отрезка FM) может быть вычислен по формуле
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит, в правой полуплоскости.
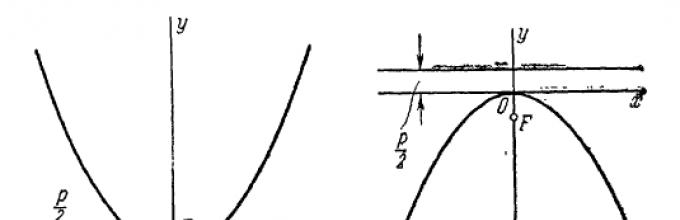
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат - с вершиной, но парабола лежит в левой полуплоскости (рис. 20), то ее уравнение будет иметь вид
у 2 = -2рх. (2)
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
если она лежит в верхней полуплоскости (рис. 21), и
Если в нижней полуплоскости (рис. 22),
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
583. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1) парабола расположена в правой полуплоскости симметрично относительно оси Ох, и ее параметр p = 3;
2) парабола расположена в левой полуплоскости симметрично относительно оси Ох, и ее параметр Р = 0,5;
3) парабола расположена в верхней полуплоскости симметрично относительно оси Оу, и ее параметр p = 1/4
4) парабола расположена в нижней полуплоскости симметрично относительно оси Оу, и ее параметр р = 3.
584. Определить величину параметра и расположение относительно координатных осей следующих парабол:
1) y 2 = 6x; 2) х 2 = 5у; 3) у 2 = - 4х; 4) х 2 = - у.
585. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:
1) парабола расположена симметрично относительно оси Ох и проходит через точку А (9; 6);
2) парабола расположена симметрично относительно оси Ох и проходит через точку В (-1;3);
3) парабола расположена симметрично относительно оси О у и проходит через точку С(1; 1).
4) парабола расположена симметрично относительно оси Оу и проходит через точку D(4;- 8).
586. Стальной трос подвешен за два конца; точки крепления расположены на одинаковой высоте; расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.
587. Составить уравнение параболы, которая имеет фокус E(0;-3) и проходит через начало координат, зная, что ее осью служит ось Оу.
588. Установить, какие линии определяются следующими уравнениями:
1) y = + 2√х; 2) у = + √ (- х); 3) у = - 3 √(- 2х);
4) y = - 2 √x; 5) x = +√(5y) 6) x = - 5√(- y);
7) х = - √(3y); 8) х = + 4√(- y);
589. Найти фокус F и уравнение директрисы параболы у 2 = 24x.
590. Вычислить фокальный радиус точки М параболы у 2 = 20х, если абсцисса точки М равна 7.
591. Вычислить фокальный радиус точки М параболы у 2 = 12х, если ордината точки М равна 6.
592. На параболе у 2 = 16x найти точки, фокальный радиус которых равен 13.
593. Составить уравнение параболы, если дан фокус F(-7;0) и уравнение директрисы х - 7 = 0.
594. Составить уравнение параболы, зная, что ее вершина совпадает с точкой (α;β), параметр равен р, ось параллельна оси Ох и парабола простирается в бесконечность:
1) в положительном направлении оси Ох;
2) в отрицательном направлении оси Ох.
595. Составить уравнение параболы, зная, что ее вершина совпадает с точкой (α;β), параметр равен р, ось параллельна оси Оу и парабола простирается в бесконечность:
1) в положительном направлении оси Оу (т. е. парабола является восходящей);
2) в отрицательном направлении оси Оу (т. е. па-рабола является нисходящей).
596. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины А, величину параметра р и уравнение директрисы: 1) y 2 = 4х - 8; 2) у 2 = 4 - 6х; 3) х 2 = 6у + 2; 4) х 2 - 2 - у.
597. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершины A и величину параметра p: 1) у = 1/4 х 2 + х + 2; 2) у = 4х 2 - 8х + 7; 3) y =-1/6 х 2 + 2х - 7.
598. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты ее вершина А и величину параметра р:1) х = 2у 2 - 12y + 14;
2) x = - 1/4y 2 + y; 3) х = -у 2 + 2у - 1.
599. Установить, какие линии определяются следую-щими уравнениями:
1) у = 3 - 4 √(х - 1); 2) х = -4 + 3√(y + 5);
3) х = 2 - √(6 - 2у); 4) y = - 5 + √(-Зх - 21).
Изобразить эти линии на чертеже.
600. Составить уравнение параболы, если даны ее фокус F(7; 2) и директриса х - 5 = 0
601. Составить уравнение параболы, если даны ее фокус F(4;3) и директриса у + 1 = 0.
602. Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса х - у - 1 = 0.
603. Даны вершина параболы A(6;-3) и уравнение ее директрисы 3x - 5у + 1 = 0, Найти фокус F этой параболы.
604. Даны вершина параболы A(-2; - 1) и урав-нение ее директрисы х + 2у - 1 = 0. Составить уравнение этой параболы.
605. Определить точки пересечения прямой x + y - 3 = 0 и параболы х 2 = 4у.
606. Определить точки пересечения прямой Зх + 4у - 12 = 0 и параболы у 2 = - 9х.
607. Определить точки пересечения прямой Зх - 2у + 6 = 0 и параболы у 2 = 6х.
608. В следующих случаях определить, как расположена данная прямая относительно данной параболы - пересекает ли, касается или проходит вне ее: 1) х - y + 2 = 0, у 2 = 8х; 2) 8х + 3y - 15 = 0, х 2 = -3у; 3) 5х -у - 15 = 0, у 2 = - 5х.
609. Определить, при каких значениях углового коэффициента k прямая y = kx + 2 1) пересекает параболу у 2 = 4х; 2) касается ее; 3) проходит вне этой параболы.
610. Вывести условие, при котором прямая у = kх + b касается параболы у 2 = 2рх.
611. Доказать, что к параболе у 2 = 2рх можно провести одну и только одну касательную с угловым коэффициентом k ≠ 0.
612. Составить уравнение касательной к параболе у 2 = 2рх в ее точке M 1 (х 1 ; у 1).
613. Составить уравнение прямой, которая касается параболы у 2 = 8х и параллельна прямой 2х + 2у - 3 = 0.
614. Составить уравнение прямой, которая касается параболы х 2 = 16у и перпендикулярна к прямой 2х+ + 4у + 7 = 0.
615. Провести касательную к параболе у 2 = 12х параллельно прямой Зх - 2y + 30 = 0 и вычислить расстояние d между этой касательной и данной прямой.
616. На параболе у 2 = 64х найти точку М 1 , ближайшую к прямой 4х + Зy - 14 = 0, и вычислить расстояние d от точки M 1 до этой прямой.
617. Составить уравнения касательных к параболе у 2 = Збх, проведенных из точки A(2; 9).
618. К параболе у 2 = 2рх проведена касательная. Доказать, что вершина этой параболы лежит посредине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.
619. Из точки А (5; 9) проведены касательные к параболе у 2 = 10х. Составить уравнение хорды, соединяющей точки касания.
620. Из точки Р(-3;12) проведены касательные к параболе у 2 = 10х. Вычислить расстояние d от точки Р до хорды параболы, соединяющей точки касания.
621. Определить точки пересечения эллипса x 2 /100 + y 2 /225 = 1 и параболы у 2 = 24x. х*
622. Определить точки пересечения гиперболы x 2 /20 - y 2 /5 = -1 и параболы у 2 = Зх
623. Определить точки пересечения двух парабол: y = х 2 - 2х+ 1, х == у 2 - 6у + 7.
624. Доказать, что прямая, касающаяся параболы в некоторой точке М, составляет равные углы с фокальным радиусом точки М и с лучом, который, исходя из М, идет параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.
625. Из фокуса параболы у 2 = 12х под острым углом α к оси Ох направлен луч света. Известно, что tgα = 3/4. Дойдя до параболы, луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.
626. Доказать, что две параболы, имеющие общую ось и общий фокус, расположенный между их вершинами, пересекаются под прямым углом.
627. Доказать, что если две параболы со взаимно перпендикулярными осями пересекаются в четырех точках, то эти точки лежат на одной окружности.
Параболой называется множество точек плоскости, равноудаленных от данной точки F этой плоскости, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Построим уравнение параболы.
Пусть
ось О
x
проходит через фокус F
параболы и
перпендикулярен директрисе, а ось Оу
проходит посередине между фокусом и
директрисой. Обозначим через p
–
расстояние
между фокусом и директрисой. Тогда
,
а уравнение директрисы
.
Ч
Пусть
– произвольная точка параболы. Пусть
– фокальный радиус точкиM
.
d
–
расстояние от точки М
до
директрисы. Тогда
По
определению параболы
.
Следовательно
Возведем это уравнение в квадрат
(20)
– каноническое уравнение параболы , симметричной относительно оси О x и проходящей через начало координат.
Точка (0; 0) – вершина параболы.
Если р > 0 ( р < 0), то парабола (20) расположена правее (левее) оси Оу .
Так
как для параболы
,
а для эллипса и гиперболы
,
то, следовательно, эксцентриситет
параболы равен 1 (
= 1).
Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением
х 2 = 2q y (21)
Фокус
этой параболы находится в точке
.
Уравнение ее директрисы
.
Фокальный радиус ее точкиМ
(х
,
у
)
выражается формулой
.
Если q > 0 (q < 0), то ветви параболы (21) расположены выше (ниже) оси Ох .
Рассмотрим примеры.
ПРИМЕР 1.
Найти координаты центра и радиус окружности, определяемой уравнением
х 2 + у 2 – 4х + 6у – 3 = 0.
Решение.
Выделим полные квадраты в данном уравнении:
х 2 + у 2 – 4х + 6у – 3 = (х 2 – 4х + 4) – 4 + (у 2 + 6у + 9) – 9 – 3 = 0
(х – 2) 2 + (у + 3) 2 = 16.
Учитывая уравнение окружности (1), имеем, что ее центр находится в точке с координатами (2; –3), а радиус равен 4.
ПРИМЕР 2.
Эллипс,
симметричный относительно осей координат,
фокусы которого находятся на оси Ох
,
проходит через точку М
(–4;
)
и имеет эксцентриситет
.
Написать уравнение эллипса и найти
фокальные радиусы точкиМ
.
Решение.
Каноническое
уравнение эллипса имеет вид
Так как эллипс проходит через точку М , то ее координаты должны удовлетворять этому уравнению
Фокусы находятся на оси Ох , следовательно
Объединив полученные два уравнения в систему, найдем а 2 и в 2:
Следовательно, уравнение данного эллипса имеет вид:
Фокальные
радиусы точки М
определим по формулам (8): х
= –4,
,
.
r
1
= а
+ х
=
=
8 – 3 = 5,
r
2
= а
– х
=
=
8 + 3 = 11.
ПРИМЕР 3.
Определить траекторию точки М , которая при своем движении остается вдвое ближе к точке F (–1; 0), чем к прямой х = –4.
Решение.
Пусть
М
(х
,
у
).
Тогда MN
= 2 MF
, MN
= –4
– x
, MF
= = 
,
–
(4 + х
)
=
.
Возведем в квадрат: (4 + х ) 2 = 4 ((х + 1) 2 + у 2),
Таким образом, точка М (х , у ) движется по эллипсу.
ПРИМЕР 4.
Написать
уравнение гиперболы, имеющей вершины
в фокусах, а фокусы – в вершинах эллипса
.
Решение.
Из уравнения данного эллипса имеем: а = 5; в = 3, а > в .
Следовательно, Поэтому, вершинами эллипса будут точки (5; 0), (0; 3), а фокусами точки F 1 (–с ; 0) = (–4; 0), F 2 (4; 0).
Так как фокусы эллипса находятся на оси Ох (а > в ), то вершины (5; 0) будут фокусами гиперболы. Каноническое уравнение гиперболы, имеющей фокусы на оси Ох , имеет вид (13)
,
причем F 1 (–5 ; 0), F 2 (5; 0) – фокусы данной гиперболы, т. е. с 1 = 5. Найдем а 1 и в 1 .
Так как вершины данной гиперболы находятся в фокусах эллипса, то а 1 = с = 4. Следовательно:
Таким образом, уравнение гиперболы имеет вид
ПРИМЕР 5.
Составить уравнение геометрического места точек, одинаково удаленных от точки F (2; 0) и от прямой у = 2. Найти вершину параболы, точки пересечения ее с осью Ох .
Р
Пусть точка М (х , у ) – принадлежит данному множеству точек.
Следовательно
FM
= NM
,
FM
=
= 
,NM
= 2 – у
,
2 – у
=
=
.
Возведем в квадрат:
– парабола, ветви которой направлены вниз.
Найдем точки пересечения данной параболы с осью Ох .
у
= 0
х
1
= 0; х
2
= 4.
Т. е. это будут точки (0; 0); (4; 0).
Вершина
параболы будет в точке с абсциссой х
= 2
=
= 2 – 1 = 1, т. е.
Вершиной параболы будет точка (2; 1).
ПРИМЕР 6.
На параболе у 2 = 6х найти точку, фокальный радиус которой равен 4,5.
Решение.
Так
как у
2
= 2рх
2р
= 6, р
= 3.
= =
Значиту
2
= 6 · 3 = 18
у
= 
=
.
(3; 
)
– две таких точки.
Лекция 2. КВАДРАТИЧНЫЕ ФОРМЫ
Рассмотрим многочлен ах 2 + bх + с, где а, b, с — числа (коэффициенты), причем а . Его обычно называют квадратным трехчленом; при этом одночлен ах 2 называют старшим членом квадратного трехчлена, а коэффициент а — старшим коэффициентом.
Функцию у = ах 2 + bх + с, где а, b, с — произвольные числа, причем а , называют квадратичной функцией. Это название можно объяснить тем, что старший член трехчлена ах 2 +bх + с содержит х в квадрате.
Опираясь на результаты, полученные выше, мы с вами сможем построить график любой квадратичной функции. Один такой график мы построили в конце предыдущего параграфа, воспользовавшись методом выделения полного квадрата. Рассмотрим еще один пример.
Пример 1. Построить график функции у = - bх 2 - 6х + 1.
Решение. Выделим полный квадрат в квадратном трехчлене -bх 2 - 6х + 1. Имеем
-Зх 2 - вх + 1 = -3(х 2 + 2х) + 1 = -3((х 2 + 2х + 1) - 1) + 1 = - 3 ((x + I) 2 - 1) + 1 = - 3 (х + I) 2 + 3 + 1 = - 3 (х + I) 2 + 4.
Для построения графика функции у = -3(х + I) 2 + 4 перейдем к вспомогательной системе координат с началом в точке (-1; 4) (пунктирные прямые х = -1 и у = 4 на рис. 61).
Привяжем функцию у = - Зх 2 к новой системе координат.
С этой целью выберем контрольные точки для функции у = - Зх 2 , например: (0; 0), (1; -3), (-1; -3), (2; -12), (-2; -12), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 61). По этим точкам построим параболу — получим требуемый график (рис. 62).
Итак, применив метод выделения полного квадрата, мы преобразовали квадратный трехчлен к виду а(х + I) 2 + m и использовали алгоритм 2 из §12 (заметим, что с равным успехом мы могли бы использовать и алгоритм 1 — кому что нравится). Оказалось что графиком функции у = -Зх 2 - 6x = 1 является парабола которая получается из параболы у = -Зх 2 параллельным переносом А в конце предыдущего параграфа мы установили, что графиком функции
у = х 2 - 4x+ 5 так же является парабола; она получается из параболы у = х 2 параллельным переносом. Оказывается график любой квадратичной функции
у = ах2+ bх + с можно получить из параболы у = ах 2 параллельным переносом, причем для доказательства этого факта используется та же идея — выделение полного квадрата.
Доказательство. Воспользуемся методом выделения полного квадрата. Имеем
Итак, нам удалось преобразовать квадратный трехчлен ах 2 + bх + с к виду а(х + I) 2 + m ,где
Чтобы построить график функции у = а(х + I) 2 + m, нужно выполнить параллельный перенос параболы у = ах2 так, чтобы вершина параболы оказалась в точке (-l; m) (рис. 63). Теорема доказана.
Обратите внимание на следующее важное обстоятельство: из проведенного доказательства следует, что вершиной параболы у = ах 2 + bх + с служит точка (-l; m). Осью параболы является прямая х = -l, т. е.
Итак, осью параболы у = ах 2 + bх + с служит прямая ; абсцисса х 0 вершины параболы у = ах 2 + bх + с вычисляется по формуле
Формулу для ординаты вершины параболы запоминать не нужно (речь идет о формуле у 0 = m, т.е. 
Во-первых, она довольно громоздкая, а во-вторых, если известна абсцисса х 0 , то ординату у 0 всегда можно вычислить по формуле
y 0 = f(х 0), где f(х) =ax 2 + bx = c,
Пример 2. Не выполняя построения графика функцииy = - 3x 2 - 6 = 1 ответить на следующие вопросы:
а) Какая прямая служит осью параболы?
б) Каковы координаты вершины параболы?
в) Куда (вверх или вниз) направлены ветви параболы?
Решение, а) Здесь а = - 3, b = - 6. Уравнение оси параболы 
б) Абсцисса х 0 вершины параболы нам уже известна: х 0 = - 1. Ординату у 0 найдем по формуле у 0 = f(x 0), где f(x) = -bх 2 - 6х + 1.
Имеем
У о = f(x о) = f(- 1) = - 3(- I) 2 - 6(- 1) + 1 = 4.
Итак, вершиной параболы служит точка (- 1; 4).
в) Парабола у = - 3х 2 - 6х + 1 получается параллельным переносом параболы у = -Зх 2 . Ветви параболы у = -Зх 2 направлены вниз (поскольку коэффициент при х 2 отрицателен), значит, и у параболы у = - Зх 2 - 6х + 1 ветви направлены вниз.
Замечание.
Сравните примеры 1 и 2. Речь в них идет об одной и той же параболе, но в примере 1 мы ее построили, а в примере 2 строить параболу было
не нужно. Проверьте по рис. 62 правильность ответов на вопросы примера 2. Для любой функции вида у = ах 2 + bх + с можно ответить на поставленные в примере 2 вопросы, не строя параболу — график функции. Легче всего ответить на вопрос, куда направлены ветви параболы:
ветви параболы у = ах 2 + bх + с направлены вверх, если а > 0, и вниз, если а < 0.
Несколько сложнее найти уравнение оси параболы: (сложнее, поскольку приходится немного посчитать). И еще сложнее (требуется больше вычислений) находятся координаты вершины параболы: абсциссой является число а ордината у 0 вычисляется по формуле у 0 = f(x 0), где f(x) = ах 2 + bх + с, 4ас-b 2
или по формуле 
ПримерЗ.
Построить график функции у = 2х 2 - 6х + 1.
Решение. Графиком функции является парабола с ветвями, направленными вверх, поскольку старший коэффициент 2 —
положительное число. Найдем координаты вершины параболы.
Имеем а = 2, b = -6;
y 0 =f(x 0) = f (1,5), где f(x) = 2х 2 -6х + 1. Значит, у 0 = f(1,5) = 2 . 1,5 2 - 6 . 1,5 + 1 = -3,5.
На рис. 64 отмечена точка (1,5; - 3,5) — вершина искомой параболы, проведена ось параболы. Чтобы построить саму параболу, поступим так: возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 0 и х = 3; вычислим значения функции в этих точках, учтя, что f (0) =f(3). Имеем f(0) = 1, значит, и f(3) = 1. Точки (0; 1) и (3; 1) отмечены на рис. 64. А теперь, зная три точки, построим искомую параболу (рис. 65)
Фактически мы получили алгоритм построения графика квадратичной функции. Оформим его.
Алгоритм построения параболы у = ах2 + bх + с
1. Найти координаты вершины параболы, построить на координатной плоскости соответствующую точку, провести ось
параболы.
2. Отметить на оси х две точки, симметричные относительно оси параболы (чаще всего в качестве одной из таких точек берут точку х = 0), найти значения
функции в этих точках; построить на координатной плоскости соответствующие точки.
3. Через полученные три точки провести параболу (в случае необходимости берут еще пару точек, симметричных от-
носительно оси параболы, и строят параболу по пяти точкам).
Пример 4.
Найти наименьшее и наибольшее значенияфункции у = - 2х 2 + 8x - 5 на отрезке .
Решение.
Первый этап.
Построим параболу, служащую графиком заданной функции. Воспользуемся алгоритмом.
1) Имеем 
Значит, вершиной параболы служит точка (2; 3), а осью параболы — прямая х = 2 (рис. 66).
2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 0 и х = 4. Имеем f(0) =f(4) = = -5; построим на координатной плоскости точки (0; - 5) и (4; - 5) (рис. 66). 
3) Через точки (2; 3), (0; -5), (4; -5) проводим параболу (рис. 67).
Второй этап.
Выделим часть построенного графика на отрезке . Замечаем (см. выделенную часть параболы на рис. 67), что у наим. = - 5 (достигается при х = 0), а y наиб. = 3 (достигается при х = 2).
Здравствуйте. В данной статье я попытаюсь показать вам возможные способы решения квадратных уравнений с помощью графиков .
Допустим, надо решить уравнение х 2 ‒ 2х ‒ 3 = 0. На этом примере мы рассмотрим варианты решения квадратного уравнения графически.
1) Можно представить наше уравнение в виде х 2 = 2х + 3. Далее построим в одной системе координат графики функций у = х 2 и у = 2х + 3. График у = х 2 представлен на рисунке 1, а оба графика на рисунке 2.
Рисунок 1 
Рисунок 2
Графики пересекаются в двух точках, наше уравнение имеет решение х = – 1 и х = 3.
2) А ведь можно представить уравнение и по - другому, например х 2 ‒ 2х = 3 и построить в одной системе координат графики функций у = х 2 ‒ 2х и у =3. Вы их можете увидеть на рисунках 3 и 4. На рисунке 3 изображен график у = х 2 ‒ 2х, а на рисунке 4 оба графика у = х 2 ‒ 2х и у =3.
Рисунок 3 
Рисунок 4
Как мы видим, эти два графика так же пересекаются в двух точках, где х = -1 и х = 3. Значит ответ: - 1; 3.
3) Есть и другой вариант представления этого уравнения х 2 ‒ 3 = 2х. И снова строим графики функций у = х 2 ‒ 3 и у = 2х в одной системе координат. Первый у = х 2 ‒ 3 на рисунке 5 и оба графика на рисунке 6.
Рисунок 5 
Рисунок 6
Ответ: - 1; 3.
4) Можно построить параболу у = х 2 ‒ 2х ‒ 3.
Вершина параболы х 0 = - b/2а = 2/2=1, у 0 = 1 2 ‒ 2·1 ‒ 3 = 1 – 2 – 3 = ‒ 4. Это точка (1; ‒ 4). Тогда наша парабола симметрична относительно прямой х =1. Если взять две точки симметричные относительно прямой х = 1 например: х = - 2 и х = 4, то мы получим две точки через которые проходят ветви графика.
Если х = -2, то у =(- 2) 2 ‒ 2(-2) ‒ 3 = 4 + 4 – 3 = 5.
Аналогично х =4, у = 4 2 ‒ 2 · 4 ‒ 3= 16 – 8 – 3 = 5. Полученные точки (-2; 5); (1; 4) и (4; 5) отмечаем в на плоскости и проводим параболу рисунок 7.
Рисунок 7
Парабола пересекает ось абсцисс в точках – 1 и 3. Это и есть корни уравнения х 2 ‒ 2х ‒ 3 = 0.
Ответ: – 1 и 3.
5) А можно выделить квадрат двучлена:
х 2 ‒ 2х ‒ 3= 0
(х 2 ‒ 2х + 1) ‒1 ‒ 3= 0
(х -1) 2 - 4 = 0
Затем построить в одной системе координат графики функций у = (х - 1) 2 и у = 4. Первый график у = (х - 1) 2 на рисунке 8, а оба графика у = (х - 1) 2 и у = 4 на рисунке 9.
Рисунок 8 
Рисунок 9
Они также пересекаются в двух точках, в которых х = -1 , х = 3.
Ответ: - 1; 3.
6) Так как х = 0 не является корнем уравнения х 2 ‒ 2х ‒ 3 = 0 (иначе выполнялось бы равенство 0 2 – 2· 0 –3 = 0), то можно все члены уравнения разделить на х. В результате мы получим уравнение х – 2 – 3/х = 0. Перенесем 3/х вправо и получаем уравнение х – 2 = 3/х Тогда можно построить в одной системе координат графики функций у = 3/х и у = х – 2.
На рисунке 10 изображен график функции у = 3/х, а на рисунке 11 оба графика функций у = 3/х и у = х – 2.
Рисунок 10 
Рисунок 11
Они также пересекаются в двух точках, в которых х = -1 , х = 3.
Ответ: - 1; 3.
Если вы были внимательны, то обратили внимание, что каким бы образом вы не представили бы уравнение в виде двух функций, у вас всегда будет один и тот же ответ (разуметься, что вы не допустите ошибок при переносе выражений из одной части уравнения в другую и при построении графиков). Поэтому, решая графически уравнение, выбирайте способ представления функций графики которых вам легче построить. И еще одно замечание если корни уравнения не целые числа, то ответ получится не точным.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |
