В этой статье мы покажем, как даются определения синуса, косинуса, тангенса и котангенса угла и числа в тригонометрии . Здесь же мы поговорим об обозначениях, приведем примеры записей, дадим графические иллюстрации. В заключение проведем параллель между определениями синуса, косинуса, тангенса и котангенса в тригонометрии и геометрии.
Навигация по странице.
Определение синуса, косинуса, тангенса и котангенса
Проследим за тем, как формируются представление о синусе, косинусе, тангенсе и котангенсе в школьном курсе математики. На уроках геометрии дается определение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. А позже изучается тригонометрия, где говорится о синусе, косинусе, тангенсе и котангенсе угла поворота и числа. Приведем все эти определения, приведем примеры и дадим необходимые комментарии.
Острого угла в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin , cos , tg и ctg соответственно.
Например, если АВС – прямоугольный треугольник с прямым углом С , то синус острого угла A равен отношению противолежащего катета BC к гипотенузе AB , то есть, sin∠A=BC/AB .
Эти определения позволяют вычислять значения синуса, косинуса, тангенса и котангенса острого угла по известным длинам сторон прямоугольного треугольника, а также по известным значениям синуса, косинуса, тангенса, котангенса и длине одной из сторон находить длины других сторон. Например, если бы мы знали, что в прямоугольном треугольнике катет AC равен 3 , а гипотенуза AB равна 7 , то мы могли бы вычислить значение косинуса острого угла A по определению: cos∠A=AC/AB=3/7 .
Угла поворота
В тригонометрии на угол начинают смотреть более широко - вводят понятие угла поворота . Величина угла поворота, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов, угол поворота в градусах (и в радианах) может выражаться каким угодно действительным числом от −∞ до +∞ .
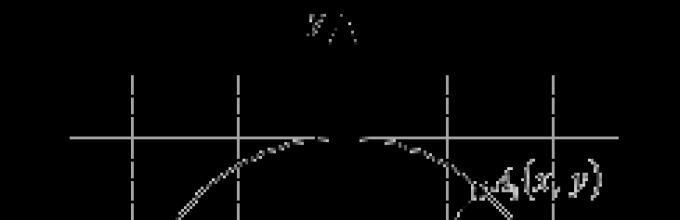
В этом свете дают определения синуса, косинуса, тангенса и котангенса уже не острого угла, а угла произвольной величины - угла поворота. Они даются через координаты x и y точки A 1 , в которую переходит так называемая начальная точка A(1, 0) после ее поворота на угол α вокруг точки O – начала прямоугольной декартовой системы координат и центра единичной окружности .
Определение.
Синус угла поворота α - это ордината точки A 1 , то есть, sinα=y .
Определение.
Косинусом угла поворота α называют абсциссу точки A 1 , то есть, cosα=x .
Определение.
Тангенс угла поворота α - это отношение ординаты точки A 1 к ее абсциссе, то есть, tgα=y/x .
Определение.
Котангенсом угла поворота α называют отношение абсциссы точки A 1 к ее ординате, то есть, ctgα=x/y .
Синус и косинус определены для любого угла α , так как мы всегда можем определить абсциссу и ординату точки, которая получается в результате поворота начальной точки на угол α . А тангенс и котангенс определены не для любого угла. Тангенс не определен для таких углов α , при которых начальная точка переходит в точку с нулевой абсциссой (0, 1) или (0, −1) , а это имеет место при углах 90°+180°·k , k∈Z (π/2+π·k рад). Действительно, при таких углах поворота выражение tgα=y/x не имеет смысла, так как в нем присутствует деление на нуль. Что же касается котангенса, то он не определен для таких углов α , при которых начальная точка переходит к в точку с нулевой ординатой (1, 0) или (−1, 0) , а это имеет место для углов 180°·k , k∈Z (π·k рад).
Итак, синус и косинус определены для любых углов поворота, тангенс определен для всех углов, кроме 90°+180°·k , k∈Z (π/2+π·k рад), а котангенс – для всех углов, кроме 180°·k , k∈Z (π·k рад).
В определениях фигурируют уже известные нам обозначения sin , cos , tg и ctg , они используются и для обозначения синуса, косинуса, тангенса и котангенса угла поворота (иногда можно встретить обозначения tan и cot , отвечающие тангенсу и котангенсу). Так синус угла поворота 30 градусов можно записать как sin30° , записям tg(−24°17′) и ctgα отвечают тангенс угла поворота −24 градуса 17 минут и котангенс угла поворота α . Напомним, что при записи радианной меры угла обозначение «рад» часто опускают. Например, косинус угла поворота в три пи рад обычно обозначают cos3·π .
В заключение этого пункта стоит заметить, что в разговоре про синус, косинус, тангенс и котангенс угла поворота часто опускают словосочетание «угол поворота» или слово «поворота». То есть, вместо фразы «синус угла поворота альфа» обычно используют фразу «синус угла альфа» или еще короче – «синус альфа». Это же касается и косинуса, и тангенса, и котангенса.
Также скажем, что определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике согласуются с только что данными определениями синуса, косинуса, тангенса и котангенса угла поворота величиной от 0 до 90 градусов. Это мы обоснуем .
Числа
Определение.
Синусом, косинусом, тангенсом и котангенсом числа t называют число, равное синусу, косинусу, тангенсу и котангенсу угла поворота в t радианов соответственно.
Например, косинус числа 8·π по определению есть число, равное косинусу угла в 8·π рад. А косинус угла в 8·π рад равен единице, поэтому, косинус числа 8·π равен 1 .
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Он состоит в том, что каждому действительному числу t ставится в соответствие точка единичной окружности с центром в начале прямоугольной системы координат, и синус, косинус, тангенс и котангенс определяются через координаты этой точки. Остановимся на этом подробнее.
Покажем, как устанавливается соответствие между действительными числами и точками окружности:
- числу 0 ставится в соответствие начальная точка A(1, 0) ;
- положительному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении против часовой стрелки и пройдем путь длиной t ;
- отрицательному числу t ставится в соответствие точка единичной окружности, в которую мы попадем, если будем двигаться по окружности из начальной точки в направлении по часовой стрелке и пройдем путь длиной |t| .
Теперь переходим к определениями синуса, косинуса, тангенса и котангенса числа t . Допустим, что числу t соответствует точка окружности A 1 (x, y) (например, числу &pi/2; отвечает точка A 1 (0, 1) ).
Определение.
Синусом числа t называют ординату точки единичной окружности, соответствующей числу t , то есть, sint=y .
Определение.
Косинусом числа t называют абсциссу точки единичной окружности, отвечающей числу t , то есть, cost=x .
Определение.
Тангенсом числа t называют отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t , то есть, tgt=y/x . В другой равносильной формулировке тангенс числа t – это отношение синуса этого числа к косинусу, то есть, tgt=sint/cost .
Определение.
Котангенсом числа t называют отношение абсциссы к ординате точки единичной окружности, соответствующей числу t , то есть, ctgt=x/y . Другая формулировка такова: тангенс числа t – это отношение косинуса числа t к синусу числа t : ctgt=cost/sint .
Здесь отметим, что только что данные определения согласуются с определением, данным в начале этого пункта. Действительно, точка единичной окружности, соответствующая числу t , совпадает с точкой, полученной в результате поворота начальной точки на угол в t радианов.
Еще стоит прояснить такой момент. Допустим, перед нами запись sin3 . Как понять, о синусе числа 3 или о синусе угла поворота в 3 радиана идет речь? Обычно это ясно из контекста, в противном случае это скорее всего не имеет принципиального значения.
Тригонометрические функции углового и числового аргумента
Согласно данным в предыдущем пункте определениям, каждому углу поворота α соответствуют вполне определенное значение sinα , как и значение cosα . Кроме того, всем углам поворота, отличным от 90°+180°·k , k∈Z (π/2+π·k рад) отвечают значения tgα , а отличным от 180°·k , k∈Z (π·k рад) – значения ctgα . Поэтому sinα , cosα , tgα и ctgα - это функции угла α . Другими словами – это функции углового аргумента.
Аналогично можно говорить и про функции синус, косинус, тангенс и котангенс числового аргумента. Действительно, каждому действительному числу t отвечает вполне определенное значение sint , как и cost . Кроме того, всем числам, отличным от π/2+π·k , k∈Z соответствуют значения tgt , а числам π·k , k∈Z - значения ctgt .
Функции синус, косинус, тангенс и котангенс называют основными тригонометрическими функциями .
Из контекста обычно понятно, с тригонометрическими функциями углового аргумента или числового аргумента мы имеем дело. В противном случае мы можем считать независимую переменную как мерой угла (угловым аргументом), так и числовым аргументом.
Однако, в школе в основном изучаются числовые функции, то есть, функции, аргументы которых, как и соответствующие им значения функции, являются числами. Поэтому, если речь идет именно о функциях, то целесообразно считать тригонометрические функции функциями числовых аргументов.
Связь определений из геометрии и тригонометрии
Если рассматривать угол поворота α величиной от 0 до 90 градусов, то данные в контексте тригонометрии определения синуса, косинуса, тангенса и котангенса угла поворота полностью согласуются с определениями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, которые даются в курсе геометрии. Обоснуем это.
Изобразим в прямоугольной декартовой системе координат Oxy единичную окружность. Отметим начальную точку A(1, 0) . Повернем ее на угол α величиной от 0 до 90 градусов, получим точку A 1 (x, y) . Опустим из точки А 1 на ось Ox перпендикуляр A 1 H .

Легко видеть, что в прямоугольном треугольнике угол A 1 OH равен углу поворота α , длина прилежащего к этому углу катета OH равна абсциссе точки A 1 , то есть, |OH|=x , длина противолежащего к углу катета A 1 H равна ординате точки A 1 , то есть, |A 1 H|=y , а длина гипотенузы OA 1 равна единице, так как она является радиусом единичной окружности. Тогда по определению из геометрии синус острого угла α в прямоугольном треугольнике A 1 OH равен отношению противолежащего катета к гипотенузе, то есть, sinα=|A 1 H|/|OA 1 |=y/1=y . А по определению из тригонометрии синус угла поворота α равен ординате точки A 1 , то есть, sinα=y . Отсюда видно, что определение синуса острого угла в прямоугольном треугольнике эквивалентно определению синуса угла поворота α при α от 0 до 90 градусов.
Аналогично можно показать, что и определения косинуса, тангенса и котангенса острого угла α согласуются с определениями косинуса, тангенса и котангенса угла поворота α .
Список литературы.
- Геометрия. 7-9 классы : учеб. для общеобразоват. учреждений / [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. - 20-е изд. М.: Просвещение, 2010. - 384 с.: ил. - ISBN 978-5-09-023915-8.
- Погорелов А. В. Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/ А. В. Погорелов. - 2-е изд - М.: Просвещение, 2001. - 224 с.: ил. - ISBN 5-09-010803-X.
- Алгебра и элементарные функции : Учебное пособие для учащихся 9 класса средней школы / Е. С. Кочетков, Е. С. Кочеткова; Под редакцией доктора физико-математических наук О. Н. Головина.- 4-е изд. М.: Просвещение, 1969.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Мордкович А. Г. Алгебра и начала анализа. 10 класс. В 2 ч. Ч. 1: учебник для общеобразовательных учреждений (профильный уровень)/ А. Г. Мордкович, П. В. Семенов. - 4-е изд., доп. - М.: Мнемозина, 2007. - 424 с.: ил. ISBN 978-5-346-00792-0.
- Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни /[Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. - 3-е изд. - И.: Просвещение, 2010.- 368 с.: ил.- ISBN 978-5-09-022771-1.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - 3-е изд. - М.: Просвещение, 1993. - 351 с.: ил. - ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
1. Общие положения
1.1. С целью поддержания деловой репутации и обеспечения выполнения норм федерального законодательства ФГАУ ГНИИ ИТТ «Информика» (далее – Компания) считает важнейшей задачей обеспечение легитимности обработки и безопасности персональных данных субъектов в бизнес-процессах Компании.
1.2. Для решения данной задачи в Компании введена, функционирует и проходит периодический пересмотр (контроль) система защиты персональных данных.
1.3. Обработка персональных данных в Компании основана на следующих принципах:
Законности целей и способов обработки персональных данных и добросовестности;
Соответствия целей обработки персональных данных целям, заранее определенным и заявленным при сборе персональных данных, а также полномочиям Компании;
Соответствия объема и характера обрабатываемых персональных данных, способов обработки персональных данных целям обработки персональных данных;
Достоверности персональных данных, их актуальности и достаточности для целей обработки, недопустимости обработки избыточных по отношению к целям сбора персональных данных;
Легитимности организационных и технических мер по обеспечению безопасности персональных данных;
Непрерывности повышения уровня знаний работников Компании в сфере обеспечения безопасности персональных данных при их обработке;
Стремления к постоянному совершенствованию системы защиты персональных данных.
2. Цели обработки персональных данных
2.1. В соответствии с принципами обработки персональных данных, в Компании определены состав и цели обработки.
Цели обработки персональных данных:
Заключение, сопровождение, изменение, расторжение трудовых договоров, которые являются основанием для возникновения или прекращения трудовых отношений между Компанией и ее работниками;
Предоставление портала, сервисов личного кабинета для учеников, родителей и учителей;
Хранение результатов обучения;
Исполнение обязательств, предусмотренных федеральным законодательством и иными нормативными правовыми актами;
3. Правила обработки персональных данных
3.1. В Компании осуществляется обработка только тех персональных данных, которые представлены в утвержденном Перечне персональных данных, обрабатываемых в ФГАУ ГНИИ ИТТ «Информика»
3.2. В Компании не допускается обработка следующих категорий персональных данных:
Расовая принадлежность;
Политические взгляды;
Философские убеждения;
О состоянии здоровья;
Состояние интимной жизни;
Национальная принадлежность;
Религиозные убеждения.
3.3. В Компании не обрабатываются биометрические персональные данные (сведения, которые характеризуют физиологические и биологические особенности человека, на основании которых можно установить его личность).
3.4. В Компании не осуществляется трансграничная передача персональных данных (передача персональных данных на территорию иностранного государства органу власти иностранного государства, иностранному физическому лицу или иностранному юридическому лицу).
3.5. В Компании запрещено принятие решений относительно субъектов персональных данных на основании исключительно автоматизированной обработки их персональных данных.
3.6. В Компании не осуществляется обработка данных о судимости субъектов.
3.7. Компания не размещает персональные данные субъекта в общедоступных источниках без его предварительного согласия.
4. Реализованные требования по обеспечению безопасности персональных данных
4.1. С целью обеспечения безопасности персональных данных при их обработке в Компании реализуются требования следующих нормативных документов РФ в области обработки и обеспечения безопасности персональных данных:
Федеральный закон от 27.07.2006 г. № 152-ФЗ «О персональных данных»;
Постановление Правительства Российской Федерации от 1 ноября 2012 г. N 1119 "Об утверждении требований к защите персональных данных при их обработке в информационных системах персональных данных";
Постановление Правительства Российской Федерации от 15.09.2008 г. №687 «Об утверждении Положения об особенностях обработки персональных данных, осуществляемой без использования средств автоматизации»;
Приказ ФСТЭК России от 18.02.2013 N 21 "Об утверждении Состава и содержания организационных и технических мер по обеспечению безопасности персональных данных при их обработке в информационных системах персональных данных";
Базовая модель угроз безопасности персональных данных при их обработке в информационных системах персональных данных (утверждена заместителем директора ФСТЭК России 15.02.2008 г.);
Методика определения актуальных угроз безопасности персональных данных при их обработке в информационных системах персональных данных (утверждена заместителем директора ФСТЭК России 14.02.2008 г.).
4.2. Компания проводит оценку вреда, который может быть причинен субъектам персональных данных и определяет угрозы безопасности персональных данных. В соответствии с выявленными актуальными угрозами Компания применяет необходимые и достаточные организационные и технические меры, включающие в себя использование средств защиты информации, обнаружение фактов несанкционированного доступа, восстановление персональных данных, установление правил доступа к персональным данным, а также контроль и оценку эффективности применяемых мер.
4.3. В Компании назначены лица, ответственные за организацию обработки и обеспечения безопасности персональных данных.
4.4. Руководство Компании осознает необходимость и заинтересовано в обеспечении должного как с точки зрения требований нормативных документов РФ, так и обоснованного с точки зрения оценки рисков для бизнеса уровня безопасности персональных данных, обрабатываемых в рамках выполнения основной деятельности Компании.
Чтобы изучить основные термины и свойства такого важного раздела геометрии, как тригонометрия, необходимо тщательно отметить особенности прямоугольного треугольника, а также определения его элементов.
Прямоугольным называется треугольник, у которого один из углов равен 90 градусам, соответственно, сумма двух других равна 90 - из свойства всех треугольников об общей сумме углов. Обычно этот прямой угол обозначается буквой С. На видео представлен прямоугольный треугольник АВС с углом С = 90 градусов. Сторона, лежащая напротив прямого угла, именуется гипотенузой треугольника, а две другие стороны - его катетами. В нашем случае, АВ - это гипотенуза, а АС и ВС - катеты прямоугольного треугольника АВС.

Главными тригонометрическими показателями являются синус, косинус и тангенс угла. Сразу же важно отметить, что эти понятия характеризуют абсолютно любой плоский угол по отдельности или в составе любого многоугольника. Однако, задаются они всегда через прямоугольный треугольник.
Синусом угла называется соотношение противолежащего катета к гипотенузе. Разумеется, если угол простой и отдельный, либо же является частью иной фигуры, синус задается только после дорисовки направляющих и образования полноценного прямоугольного треугольника. На представленной иллюстрации, sin АВС (В) = АС/АВ. Для вычисления синуса достаточно поделить линейные размеры отрезков, но их размерность в тригонометрии не имеет значения, поэтому, синус и все иные показатели этого ряда являются безразмерными значениями.

Косинусом угла называют соотношение прилежащего катета к гипотенузе. В нашем случае сos АВС (В) = СВ/АВ. Тангенсом угла называют соотношение противолежащего катета к прилежащему, т.е. tg АВС (В) = АС/СВ. Размерность и вычисления аналогичны таковым у синуса. Кроме того существует ещё понятие котангенса и нескольких других тригонометрических показателей, однако они все имеют второстепенную роль.
В нашем треугольнике АВС можно вычислить синус, косинус и тангенс для иного угла:
sin САВ (А) = СВ/АВ
cos САВ (А) = СА/АВ
tg САВ (А) = СВ/СА
Основное тригонометрическое равенство, которое мы рассмотрим более подробно, вытекает из определений синуса и косинуса, а также из знаменитой теоремы Пифагора. Для того, чтобы вывести тождество, необходимо вспомнить теорему прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Иначе говоря, АВ2 = АС2 + СВ2 для треугольника АВС при прямом угле С. Используя определения синуса, косинуса, и теорему Пифагора, получим для угла А:
sin В = АС/АВ
cos В = СВ/АВ
АВ2 = АС2 + СВ2
sin 2 В + cos 2 В = (АС/АВ) 2 + (СВ/АВ) 2 = АС 2 /АВ 2 + СВ 2 /АВ 2 = (АС 2 + СВ 2)/АВ 2 = АВ 2 /АВ 2 = 1
Таким образом, sin 2 В + cos 2 В = 1. Это и есть главное тригонометрическое тождество, которое можно обозначить в словесном виде: сумма квадратов синуса и косинуса одного угла равна единице.

Предположим, что у нас есть несколько прямоугольных треугольников разной величины, но при условии, что один из их углов равен у всех. Если у треугольника равны между собой два угла, то равен и третий (по свойству постоянной суммы углов), а сами треугольники являются подобными между собой. У подобных треугольников, по определению, стороны соотносятся пропорционально. Эта пропорция сохраняется и в соотношениях для определения тригонометрических показателей. Поэтому синус, косинус, тангенс и другие показатели тригонометрии равны для любого прямоугольного треугольника, да и вообще, являются постоянной характеристикой. Значения эти зависят исключительно от градусной меры самого угла.
Вспомним школьный курс математики и поговорим о том, что такое тангенс и как найти тангенс угла. Сначала определим, что называется тангенсом. В прямоугольном треугольнике тангенсом острого угла является отношение противолежащего катета к прилежащему. Прилежащим катетом является тот, который участвует в образовании угла, противолежащим — тот, который расположен напротив угла.
Также тангенсом острого угла является отношение синуса этого угла к его косинусу. Для понимания напомним, что является синусом и косинусом угла. Синусом острого угла в прямоугольном треугольнике является отношение противолежащего катета к гипотенузе, косинус — это отношение прилежащего катета к гипотенузе.
Есть еще котангенс, он противоположен тангенсу. Котангенсом является отношение прилежащего катета к противолежащему и соответственно отношение косинуса угла к его синусу.
Синус, косинус, тангенс и котангенс являются тригонометрическими функциями угла, они показывают соотношения между углами и сторонами треугольника, помогают вычислять стороны треугольника.
Вычисляем тангенс острого угла
Как найти тангенс в треугольнике? Чтобы не тратить время на поиски тангенса, можно найти специальные таблицы, где указаны тригонометрические функции многих углов. В школьных задачках по геометрии очень распространены определенные углы, и значения их синусов, косинусов, тангенсов и котангенсов учителя просят запомнить. Мы предлагаем вам небольшую табличку с нужными значениями эти углов.
Если же угол, тангенс которого нужно найти, не представлен в этой таблице, то можно воспользоваться двумя формулами, которые мы и представили выше в словесной форме.
Первый способ вычислить тангенс угла — это поделить длину противолежащего катета на длину прилежащего. Допустим, противолежащий катет равен 4, а прилежащий 8. Чтобы найти тангенс, надо 4:8. Тангенс угла будет равен ½ или 0,5.
Второй способ вычисления тангенса — это поделить значение синуса данного угла на значение его косинуса. Например, нам дан угол в 45 градусов. Его sin = корень из двух, поделенный на два; его cos равен тому же числу. Теперь делим синус на косинус и получаем тангенс, равный единице.
Бывает, что нужно воспользоваться именно этой формулой, но известен только один элемент — или синус, или косинус. В таком случае будет полезно вспомнить формулу
sin2 α + cos2 α = 1. Это основное тригонометрическое тождество. Выражая неизвестный элемент через известный, можно выяснить его значение. А зная синус и косинус, найти тангенс уже нетрудно.
А если геометрия — это явно не ваше призвание, но сделать домашнее задание все же нужно, то можно воспользоваться онлайн-калькулятором расчета тангенса угла .
Мы рассказали вам на простых примерах, как находить тангенс. Однако условия задач бывают труднее и не всегда можно быстро выяснить все необходимые данные. В этом случае вам поможет теорема Пифагора и различные тригонометрические функции.





 Назад
Вперёд
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- ввести понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника;
- показать, как используются синус, косинус и тангенс при решении задач;
- развитие умений наблюдать, сравнивать, анализировать и делать вывод.
Ход урока
Актуализация знаний (определение основной проблемы урока)
Проводится в форме фронтального опроса.
Учитель. На доске вы видите краткую запись 6 задач < Рисунок 1>. Вспомните, какие из этих задач вы уже умеете решать? Решите эти задачи. Сформулируйте соответствующие теоремы.

Рисунок 1
Учащиеся:
Задача 1. Ответ: 5. В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
Задача 2. Ответ: 41°. Сумма внутренних углов треугольника равна 180°.
Задача 3. Ответ: 10 . Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Задачи 4-6 мы не можем решить.
Учитель. А почему вы не сумеете решить задачи 4-6? Какой вопрос возникает?
Учащиеся. Мы не знаем, что такое tgB, sinA, cosB.
Учитель. sinА, cosB, tgB читается: “синус угла А”, “косинус угла В” и “тангенс угла В”. Мы сегодня узнаем, что означает каждое из этих выражений, и научимся решать задачи типа 4-6.
Введение нового материала
Проводится в форме эвристической беседы.
Учитель. Начертите прямоугольные треугольники с катетами 3 и 4, 6 и 8. Обозначьте их АВС и А 1 В 1 С 1 так, чтобы В и В 1 были углами, противолежащими катетам 4 и 8, а прямыми углами были С, С 1 . Равны ли углы В и В 1 ? Почему?
Учащиеся . Равны, потому что треугольники подобны. AC: BC = A 1 C 1: B 1 C 1 (3: 4 = 6: 8) и углы между ними прямые.<Рисунок 2>
Учитель . Равенства каких ещё отношений следуют из подобия треугольников АВС и А 1 В 1 С 1 ?
Учащиеся . ВС: АВ = В 1 С 1: А 1 В 1 , АС: АВ = А 1 С 1: А 1 В 1 .

Учитель . АС: АВ = А 1 С 1: А 1 В 1 = sinB = sinB 1.
ВС: АВ = В 1 С 1: А 1 В 1 = cosB = cosB 1 . AC: BC = A 1 C 1: B 1 C 1 = tgB = tgB 1 . Катет АС является противолежащим углу В, а катет ВС - прилежащим к этому углу. Сформулируйте определения синуса, косинуса и тангенса.
Учащиеся . Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Учитель . Запишите сами синус, косинус и тангенс угла А (слайд 1). Получились формулы (1), (2), (3) :
(1)
Итак, мы узнали что такое синус, косинус и тангенс острого угла прямоугольного треугольника. Вообще, понятия синуса косинуса и тангенса имеют длительную историю. Изучая зависимость между сторонами и углами треугольника, древние учёные нашли способы вычислений различных элементов треугольника. Эти знания, главным образом, использовались для решения задач практической астрономии, для определения недоступных расстояний.
Закрепление
Учитель . Решим задачу №591 (а,б) .
Задание выводится на экран (слайд 2). Задание “а” решается на доске с полным объяснением; “б” – самостоятельно с последующей проверкой друг друга.
Найдите синус, косинус и тангенс углов А и В треугольника АВС с прямым углом С, если: а) ВС = 8, АВ = 17; б) ВС = 21, АС = 20.
Решение. а) = . = , по теореме Пифагора найдём АС = 15,
= ; б) , по теореме Пифагора найдём АВ = 29, . . .Учитель. А теперь вернёмся к задачам 4–6 <Рисунок 1>. Давайте обсудим, что известно в задачах 4–6 и что требуется найти?
Задача 4. Что известно? Что надо найти?
Учащиеся . Известны ВС = 7 и tg В = 3,5. Надо найти АС.
Учитель . Что такое tg В?
Учащиеся . .
Учитель . Работаем с формулой. Формула состоит из трёх компонентов. Назовите их. Какие компоненты известны? Какой компонент неизвестен? Можете найти? Найдите.
Учащиеся . АС = ВС * tg B = 7 * 3,5 = 24,5
Учитель . По этому образцу решите задачи 5 и 6 <Рисунок 1>. 1 ученик работает на закрытой доске
Учитель .
1. Расскажите, удалось ли вам найти требуемые неизвестные?
2. Каков был порядок ваших действий?
3. Может быть есть другие решения?
Учащиеся .1. Да. Легко. По образцу. Задача 5. Ответ: 10. Задача 6. Ответ: 2,5
2. Сначала синус и косинус соответствующих углов заменяем по определению соответствующими отношениями, затем в полученных пропорциях проставляем известные данные, после этого находим искомые неизвестные.
Учитель . Какой общий вывод можно сделать после решения задач 4–6? Какие новые задачи мы научились решать в прямоугольном треугольнике? Подумайте и сформулируйте ваш вывод.
Учащиеся . Если в прямоугольном треугольнике известны одна сторона и отношение этой стороны к одной из других сторон, либо одна сторона и отношение одной из других сторон к известной стороне (либо синус, либо косинус, либо тангенс), то можно найти эту вторую сторону.
Решение задач.
А теперь попробуйте решить эти задачи 7–9 <Рисунок 3>.

Рисунок 3
Учащиеся . Мы не знаем, как их решать.
Учитель . Вернёмся к задаче 1 <Рисунок 1>. Изменим условие задачи. Пусть NK = 5, NM = 10. Найти угол М.
Учащиеся. Угол М равен 30°, так как катет противолежащий углу М равен половине гипотенузы.
Учитель . То есть получается, что если синус угла равен 0,5, то угол равен 30°. А теперь решим задачи №592 (а,в,д)
№592. Постройте угол a , если: а) в) д) .
Решение .
а) На сторонах прямого угла отложим отрезки длиной 1 и 2, соединим концы отрезков. В полученном треугольнике угол, лежащий против катета 1, и есть искомый угол a ;
в) 0,2 = . На одной стороне прямого угла от его вершины отложим отрезок длины 1. Построим окружность радиуса 5 с центром в конце отложенного отрезка. Точку пересечения окружности со второй стороной прямого угла соединим с концом отложенного на первой стороне угла отрезка. В полученном треугольнике угол, прилежащий катету длины 1, и есть угол a ; (слайд 4)
д) На одной стороне прямого угла от его вершины отложим отрезок длины 1. Построим окружность радиуса 2 с центром в конце отложенного отрезка. Точку пересечения окружности со второй стороной прямого угла соединим с концом отложенного на первой стороне угла отрезка. В полученном треугольнике угол, противолежащий катету длины 1, и есть искомый угол a .(слайд 5)
Вы построили углы, а значит, вы нашли углы. Их можно измерить и оформить в виде таблицы.
Аналогично можно решить задачи 7-9 <Рисунок 3>
Подведение итогов
Учитель. Ответьте на вопросы:
1. Что называется синусом, косинусом и тангенсом прямого угла в прямоугольном треугольнике?
2. В прямоугольном треугольнике 6 элементов. Какие новые задачи вы сегодня научились решать? Каков при этом порядок ваших действий? Проверьте свои умения правильно выполнять эти действия (Раздаются индивидуальные карточки).
Примерное содержание карточек: 1. В треугольнике АВС угол С прямой, ВС = 2, Найдите АВ. 2. В треугольнике АВС угол С прямой, АС = 8, . Найдите АВ. 3. В треугольнике АВС угол С равен 90°, АС = 6, . Найдите ВС.
Учащиеся сверяют свою работу с готовыми решениями на соответствующих карточках.
Задания на дом: вопрос 15 на стр.159; №591(в,г),592(б,г,е) (слайд 6)
Использованная литература
- Геометрия. 7–9 классы: учеб. для общеобразовательных организаций / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – 2-е изд. – М.: Просвещение, 2014.