Цели урока:
1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;
2) научить строить среднюю линию трапеции;
3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;
4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;
5) развивать логическое мышление, память, внимание.
Ход урока
1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:
а) определение трапеции; виды трапеций;
б) определение средней линии треугольника;
в) свойство средней линии треугольника;
г) признак средней линии треугольника.
2. Изучение нового материала.
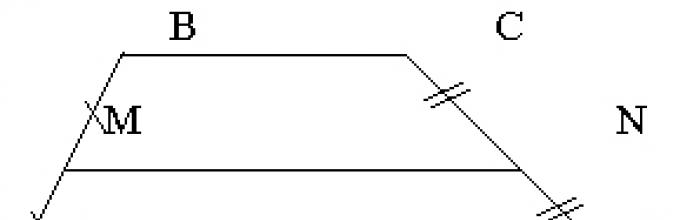
а) На доске изображена трапеция ABCD.
б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.
Ученики изображают трапецию ABCD в тетради.
в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.
д) Записывают определение средней линии трапеции, изображая её в тетради.
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.
Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Дано: ABCD – трапеция,
MN – средняя линия ABCD
Доказать , что:
1. BC || MN || AD.
2. MN = (AD + BC).
Можно выписать некоторые следствия, вытекающие из условия теоремы:
AM = MB, CN = ND, BC || AD.
На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?
Запишем дополнительное построение для одного из случаев.
Проведём прямую BN, пересекающую продолжение стороны AD в точке K.

Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия ABD, а дальше можно будет воспользоваться свойством средней линии треугольника и доказать необходимое.
Доказательство:
1. Рассмотрим BNC и DNK, в них:
а) CNB =DNK (свойство вертикальных углов);
б) BCN = NDK (свойство внутренних накрест лежащих углов);
в) CN = ND (по следствию из условия теоремы).
Значит BNC =DNK (по стороне и двум прилежащим к ней углам).
Что и требовалось доказать.
Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).
Необходимо сказать и о других возможных способ доказательства этой теоремы:
1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.

2. Провести CF || BA и рассмотреть параллелограмм ABCF и DCF.

3. Провести EF || BA и рассмотреть равенство FND и ENC.

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.
з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.
Средняя линия треугольника. Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была , в которой сии факты я предлагал просто запомнить, теперь подробнее…
Что такое средняя линия треугольника и каковы её свойства?
Определение. Средняя линия треугольника – это отрезок, соединяющий середины сторон треугольника.

Понятно, что средних линий в треугольнике три. Покажем их:

Без всяких доказательств вы уже, наверное, заметили, что все четыре образованные треугольника равны. Это так, но подробнее об этом поговорим далее.
Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

Доказательство:
1. Давайте рассмотрим треугольники BMN и BAC. По условию у нас BM=MA, BN=NC. Можем записать:

Следовательно треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А то что:
По признаку параллельности прямых MN||AC.
2. Также из подобия треугольников следует, что
То есть MN в два раза меньше. Доказано!
Решим типичную задачу.
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC. Найти периметр треугольника ABC, если MN=12, MK=10, KN=8.
Решение. Конечно, прежде всего следует проверить существование треугольника MNK (а значит и существование треугольника АВС). Сумма двух меньших сторон должна быть более третьей стороны, записываем 10+8>12. Выполнятся, следовательно треугольник существует.
Построим эскиз:

Таким образом периметр треугольника АВС равен 24+20+16=60.
*Теперь подробнее о треугольниках полученных при построении всех трёх средних линий. Их равенство легко доказывается. Посмотрите:

Равны они по трём сторонам. Конечно, и другие признаки здесь применимы. Получаем, что
Как это свойство используется в заданиях включённых в состав экзамена? Особо хочется заострить внимание на задачах по стереометрии. Есть такие типы, в которых речь идет о треугольной призме.
Например, сказано что плоскость проходит через середины сторон основания и она параллельна третьему ребру основания. Ставятся вопросы о изменении площади поверхности призмы, её объёма и другие.
Так вот. Зная и понимая информацию изложенную выше вы сразу же определите, что эта плоскость отсекает от основания указанной призмы одну четвёртую часть и задачу решите устно. Вот с такими задачами.
На этом всё! Всего доброго!
Скачать материал статьи
С уважением, Александр Крутицких.
Понятие средней линии треугольника
Введем понятие средней линии треугольника.
Определение 1
Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).
Рисунок 1. Средняя линия треугольника
Теорема о средней линии треугольника
Теорема 1
Средняя линия треугольника параллельна одной из его сторон и равна её половине.
Доказательство.
Пусть нам дан треугольник $ABC$. $MN$ - средняя линия (как на рисунке 2).

Рисунок 2. Иллюстрация теоремы 1
Так как $\frac{AM}{AB}=\frac{BN}{BC}=\frac{1}{2}$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит
Также, отсюда следует, что $\angle A=\angle BMN$, значит $MN||AC$.
Теорема доказана.
Следствия из теоремы о средней линии треугольника
Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.
Доказательство.
Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).

Рисунок 3. Иллюстрация следствия 1
По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда
Аналогично доказывается, что
Теорема доказана.
Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac{1}{2}$.
Доказательство.
Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ (рис. 4)

Рисунок 4. Иллюстрация следствия 2
Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ - средняя линия, то
Угол $C$ - общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=\frac{1}{2}$.
Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ {\ A}_1C_1,\ B_1C_1$ -- средние линии треугольника, то
Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=\frac{1}{2}$.
Теорема доказана.
Примеры задачи на понятие средней линии треугольника
Пример 1
Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника , вершины которого лежат в серединах сторон данного треугольника.
Решение.
Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны -- средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.
Ответ: $20$ см.
Пример 2
Дан треугольник $ABC$. Точки $N\ и\ M$ -- середины сторон $BC$ и $AB$ соответственно (Рис. 5).

Рисунок 5.
Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.
Решение.
Так как $N\ и\ M$ -- середины сторон $BC$ и $AB$, то $MN$ -- средняя линия. Значит
По теореме 1, $AC=2MN$. Получаем:
Автомобиль проехал первую половину пути со скоростью υ 1 = 40 км/ч, вторую – со скоростью υ 2 = 60 км/ч. Найти среднюю скорость υ ср на всем пройденном пути.
Автомобиль ехал первую половину времени со скоростью υ 1 = 40 км/ч, вторую – со скоростью υ 2 = 60 км/ч. Найти среднюю скорость υ ср за все время движения.
Первую четверть пути мотоциклист двигался со скоростью 40 км/ч, оставшуюся часть пути – со скоростью 60 км/ч. Чему равна средняя скорость движения мотоциклиста на всём пути?
Точка движется по прямой в одну сторону. На рисунке показан график пройденного ею пути S от времени t . Найдите с помощью этого графика среднюю скорость υ ср за 16 секунд движения.
Когда хвост ползущего Удава поравнялся с пальмой, под которой сидела Мартышка, она, решив измерить длину Удава, побежала вдоль него и положила банан рядом с его головой. Затем Мартышка побежала обратно и положила второй банан рядом с кончиком хвоста Удава. Потом пришел Попугай и измерил расстояния от пальмы до каждого из бананов, которые оказались равными 16 и 48 попугаев. Найдите длину Удава в попугаях, а также определите, во сколько раз быстрее бегает Мартышка, чем ползает Удав.
По графикам а х =а х (t) для прямолинейного движения материальной точки построить графики зависимости υ х =υ х (t) , считая, что в начальный момент времени t = 0 скорость точки равна нулю.

Графики зависимости проекции скорости для прямолинейного движения некоторого тела от времени t изображены на рисунке. Начертить графики зависимости проекции ускорения а х , координаты тела х и пройденного пути S от времени в течение первых четырех секунд.

На рисунке даны графики зависимости от времени скоростей для двух точек, движущихся по одной прямой из одного и того же начального положения. В какой момент времени Т точки встретятся? Построить графики зависимости координат тел от времени.

Автобус, двигаясь прямолинейно со скоростью υ = 18 км/ч, проехал мимо остановки. Человек, стоявший на остановке, побежал за автобусом, двигаясь равноускоренно. С каким ускорением а должен бежать человек, чтобы догнать автобус на расстоянии S = 100 м от остановки? Какую скорость υ 1 будет иметь человек в этот момент?
Человек движется вдоль прямой дороги со скоростью υ 1 = 3,6 км/ч. Его обгоняет автомобиль, движущийся со скоростью υ 2 = 72 км/ч. Спустя время t 1 = 1 мин после этого автомобиль начинает тормозить с постоянным ускорением а = 2 м/с 2 до полной остановки. Определить расстояние S между человеком и автомобилем через t 2 = 5 мин после обгона.
1. Из пункта a в пункт Bодновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27
Документ... автомобиля . Первый проехал с постоянной скоростью весь путь . Второй проехал первую половину пути со скоростью 36 км/ч, а вторую половину пути проехал со скоростью , на 24 км/ч большей скорости первого ...
Прототипы из пункта a в пункт Bодновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со ск
ДокументДва автомобиля . Первый проехал с постоянной скоростью весь путь . Второй проехал первую половину пути со скоростью , меньшей скорости первого на 13 км/ч, а вторую половину пути - со скоростью 78 ...
- Документ
400 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь ? 3. Автомобиль проехал первую половину пути со скоростью 50 км/ч, а вторую - со скоростью 80 ...
-
С ними всё понятно, решаются довольно быстро. Но на одной задаче хотелось бы остановиться и уделить ей особое внимание. Почему? При её решении ребята ошибаются и довольно часто, опрометчиво думая что решается она устно. Посмотрите условие:
Первую половину пути автомобиль проехал со скоростью 70 км/ч, а вторую половину – со скоростью 90 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Каков ответ? Так и напрашивается – 80, не правда ли? И многие выдают именно такой результат. То есть делят сумму скоростей на 2. Это неверно!!!
Решение: Для того чтобы найти среднюю скорость необходимо всё пройденное расстояние разделить на сумму отрезков времени соответствующих каждому пройденному участку пути. Для двух участков пути формула такова:

Расстояние нам не дано. Примем его за S км. Тогда время затраченное на первую половину пути будет равно:
 Время затраченное на вторую половину пути равно:
Время затраченное на вторую половину пути равно: Таким образом:
Таким образом:
Ответ: 78,75
Решение в общем виде: если принять скорость на первой половине пути как V 1 , а на второй как V 2 , то получим что средняя скорость будет равна:

А теперь такая задача!
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61 км/ч, а вторую половину времени – со скоростью 87 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о двух участках пути. Среднюю скорость будем вычислять по формуле:

Пусть на весь путь автомобиль затратил t часов.
Тогда за первую половину времени со скоростью 61 км/ч автомобиль прошёл 0,5t∙61 километров, а за вторую половину времени 0,5t∙87 километров, значит:
*Вариант второй.
Пусть S 1 первый участок пути, S 2 это второй участок пути, тогда
 По условию
По условию
Вот в этом случае средняя скорость равна полусумме скоростей. Обратили внимание на отличие в условиях?
ЗАДАЧА 1: «Первую половину пути автомобиль ехал со скоростью 70 км/ч, а вторую половину – со скоростью 90 км/ч.»
ЗАДАЧА 2: «Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61 км/ч, а вторую половину времени – со скоростью 87 км/ч.»
В первой говорится о половинах пути, а во второй о половинах времени. Отложите эти моменты в памяти.
Кстати, задача про путешественника, который преодолел море и вернулся обратно относится к первому типу.
Теперь решите для закрепления материала.
Рыбак переплыл на катере реку со скоростью 60 км/ч. Обратно он переехал её по мосту на автомобиле со скоростью 140 км/ч. Найдите среднюю скорость рыбака на протяжении всего пути. Ответ дайте в км/ч.
Решение: Расстояние одинаково туда и обратно. Пусть расстояние между берегами равно S км. Тогда время затраченное на катере равно S/60 часов, а время затраченное на обратный путь равно S/140 часов.
Расстояние которое преодолел рыбак равно 2S км (туда и обратно). Тогда средняя скорость равна:
На этом всё. Успехов вам!
С уважением, Александр.