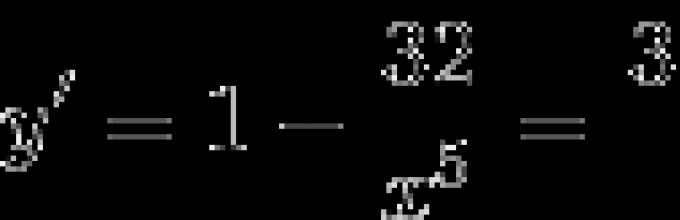С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word . Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f" 0 (x *) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:F" 0 (x *) = 0
f"" 0 (x *) > 0
То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F" 0 (x *) = 0
f"" 0 (x *) < 0
То точка x * - локальный (глобальный) максимум.
Пример №1
. Найти наибольшее и наименьшее значения функции:
на отрезке .
Решение.
![]()
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1
Пример №2
. С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; ![]() , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
, значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
Пример №3
. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Значение функции в точке max явл наибольшим лишь в некоторой окрестности этой точки и совсем не обязательно явл. наибольшим значением во всей области определения ф-ии. То же самое можно сказать и о минимуме. В этом случае их назыв часто локальными (местными) max и min в отличии от абсолютных, т.е. - наибольшее и наименьшее знач. во всей обл определения. Если функция f(x) задана на а,в и непрерывна на нем, то она достигает на нем в каких либо точках своего наибольшего и наименьшего значений. Как их найти? Если на а,в есть несколько max, то наиб. значение внутри (если оно достигается) совпадает с одним из них. В то же время наибольшее значение для всего а,в функция может достичь и на одном из концов.
Правило..
Нужно сравнить между собой все min и граничные значения f(а) и f(в). Наименьшее значение и будет наименьшим значением функции на а,в. Обычно поступают при нахождении наиб. и наим. значений проще:
Находят все критические точки внутри сегмента а,в, вычисляют значения функции в них (не определяя есть ли в них экстремум), 2) вычисляют значение функции на концах f(а) и f(в), 3)сравнивают полученные значения между собой: наименьшее значение из этих значений и будет наименьшим значением функции, наибольшее- наибольшим на а,в.
Пример:
Наити наиб. и наименьшее значение функции у=на-1,2,
1.ищем критические точки на (-1,2).
У"= =0,
2х+2х 3 -2х 3 =0,
2х=0,
=0,
2х+2х 3 -2х 3 =0,
2х=0,
 =0.
Других нет.
=0.
Других нет.
2. f(-1)=1/2, f(2)=4/5.
f(0)=0, наименьшее значение, f(2)=4/5.- наибольшее на
Нужно
заметить следующее. В прикладных задачах
наиболее часто встречается случай,
когда между а и в функция у=f(x)
им. только одну критическую точку. В
этом случае без сравнения с граничными
значениями ясно, что если в т.
 max,
то это и есть наибольшее значение функции
на а,в,
если это min,
то это и есть наименьшее значение на
а,в.
Это важно в тех случаях, когда в выражение
функции входят буквенные выражения и
оказывается более просто исследовать
на экстремум, чем сравнивать значения
на концах.
max,
то это и есть наибольшее значение функции
на а,в,
если это min,
то это и есть наименьшее значение на
а,в.
Это важно в тех случаях, когда в выражение
функции входят буквенные выражения и
оказывается более просто исследовать
на экстремум, чем сравнивать значения
на концах.
Важно отметить, что все сказанное о нахождении наиб и наим значений применимо и к (а,в) и к бесконечному промежутку , только в этом случае не берут во внимание значения на концах.
§4.Напрвление вогнутости кривой и точки перегиба
Пусть
функция у=f(x)
им. в т. конечную производную. Тогда она им. в
этой точке касательную, уравнение
которой есть у-
конечную производную. Тогда она им. в
этой точке касательную, уравнение
которой есть у- =f
"(
=f
"( )(х-
)(х- )
или у=f(
)
или у=f( )+(х-
)+(х- )
) .
.
В
некоторой окрестности ( -
-
график функции может располагаться по
разному: либо выше касательной, либо
ниже, либо с обеих сторон.
график функции может располагаться по
разному: либо выше касательной, либо
ниже, либо с обеих сторон.
Определение.
Говорят,
что в т.М( ,
, )
кривая у=f(x)
вогнута вниз или просто вогнута (вогнута
вверх или выпукла), если для всех х из
некоторой окрестности (
)
кривая у=f(x)
вогнута вниз или просто вогнута (вогнута
вверх или выпукла), если для всех х из
некоторой окрестности ( -
-
точки
точки
 все точки кривой расположены выше
касательной (ниже касательной).
все точки кривой расположены выше
касательной (ниже касательной).
Если в т.М кривая переходит с одной стороны касательной на другую, то т.М назыв. точкой перегиба кривой.
В т.М1- кривая вогнута, М2-выпуклая, М3-перегиб.
В точке перегиба кривая меняет выпуклость на вогнутость или наоборот. Точка перегиба- пограничная между участками выпуклости и вогнутости кривой.
Определение
точки перегиба остается в силе и в
случае, когда касательная к кривой
у=f(x)
перпенд. оси ох, те в т. производнаяf
"(
производнаяf
"( )=,
и т.
)=,
и т. не явл. точкой возврата кривой. В отличии
от случаев (указанных на чертеже),
не явл. точкой возврата кривой. В отличии
от случаев (указанных на чертеже),
 x
x
x
x
где
т. и х точками перегиба не явл-ся.
и х точками перегиба не явл-ся.
Найдем
условия, при которых им. место определенное
направление вогнутости или перегиб
кривой. у=f(x)
в произвольной т.х= .
.
Пусть,
например, кривая в т.М( ,
, )
выпуклая. Тогда она располагается в
некоторой окрестности (
)
выпуклая. Тогда она располагается в
некоторой окрестности ( -
-
этой точки ниже касательной у=f(
этой точки ниже касательной у=f( )+f
"(
)+f
"( )(х-
)(х- ).
Рассмотрим вспомогательную ф-ию(х)=
f(х)-f(
).
Рассмотрим вспомогательную ф-ию(х)=
f(х)-f( )-f
"(
)-f
"( )(х-
)(х- ).
В т.
).
В т. (
( )=0,
в-окрестности
т.
)=0,
в-окрестности
т.
 .
Отсюда следует, что в точке
.
Отсюда следует, что в точке функция
функция имеетmax.
Значит в точке
имеетmax.
Значит в точке
 ""(
""( ).
Но ""(
).
Но ""( )=f
""(х) и потому в т.
)=f
""(х) и потому в т. f
""(
f
""( ).
).
Таким
образом, чтобы в т.х0 кривая у=f(x)
была выпуклой необходимо, чтобы f
""( ).
Если же в т.х0 f
""(
).
Если же в т.х0 f
""( ),
то в т.
),
то в т. -max
и кривая, значит, выпуклая. Условие f
""(
-max
и кривая, значит, выпуклая. Условие f
""( )
достаточное для выпуклости в т.
)
достаточное для выпуклости в т. .
.
Рассуждая
совершенно аналогично, получим, что
условие f
""( )
необходимое для вогнутости в т.х0, а
условие f
""(
)
необходимое для вогнутости в т.х0, а
условие f
""( )
достаточное для вогнутости.
)
достаточное для вогнутости.
Вывод:
если
в т. вторая производная положительнаf
""(
вторая производная положительнаf
""( ),
то кривая выгнута в этой точке, если в
т.
),
то кривая выгнута в этой точке, если в
т. вторая производная отрицательнаf
""(
вторая производная отрицательнаf
""( ),
то кривая выпуклая в этой точке.
),
то кривая выпуклая в этой точке.
Удобно правило "чашечки":

В
точках перегиба нет определенной
вогнутости или выпуклости, а потому они
могут быть лишь в точках, где f
""( )=0.
Но условиеf
""(
)=0.
Но условиеf
""( )
еще не обеспечивает точно, что
)
еще не обеспечивает точно, что - точка перегиба. Например, для кривых
у=х 4
и у=-х 4 ,
в т.
- точка перегиба. Например, для кривых
у=х 4
и у=-х 4 ,
в т. f
""(
f
""( )=0,
однако в ней первая кривая вогнута,
вторая выпукла.
)=0,
однако в ней первая кривая вогнута,
вторая выпукла.

Вывод:
условие f
""( )=0
явл. необходимым условием существования
перегиба в т.
)=0
явл. необходимым условием существования
перегиба в т. .
Но, как видели, т. перегиба могут быть
и там, где вторая производнаяf""(
.
Но, как видели, т. перегиба могут быть
и там, где вторая производнаяf""( )=
ил не существует вовсе.
)=
ил не существует вовсе.
Достаточным
условием перегиба кривой в т. явл. смена знака второй производнойf
""(
явл. смена знака второй производнойf
""( )
при переходе через т.
)
при переходе через т. .
При этом, если 2-ая производная меняет
при переходе через т.
.
При этом, если 2-ая производная меняет
при переходе через т. знак с + на - , то в т.
знак с + на - , то в т. перегиб со сменой вогнутости на
выпуклость, Еслиf
""(
перегиб со сменой вогнутости на
выпуклость, Еслиf
""( )
меняет знак с - на + при переходе через
т.
)
меняет знак с - на + при переходе через
т. ,
то в т.
,
то в т. перегиб со сменой выпуклости на
вогнутость..
перегиб со сменой выпуклости на
вогнутость..
Определение . Если кривая вогнута (выпукла) в каждой точке некоторого промежутка, то она назыв. вогнутой (выпуклой) на этом промежутке.
Исследование функции у=f(x) на выпуклость, вогнутость, точки перегиба проводят по следующему плану:
1.Находят все точки подозрительные на перегиб, для чего:
а) находят второю производную, приравнивают ее к нулю и находят действительные корни полученного уравнения,
б)находят точки, где конечная производная f ""(x) не сущ-ет,
2.Исследуют f ""(х) на изменение знака при переходе через каждую подозрительную на перегиб точку. Если знак меняется- перегиб есть, если нет-то нет.
Для тех точек,где f ""(х0) кривая вогнута, где наоборот -выпукла. Так же как и в случае экстремумов, если точек подозрительных на перегиб конечное число, пользуются методом интервалов.
Определение.
Если кривая выпукла (вогнута) в каждой точке некоторого промежутка, она назыв. выпуклой (вогнутой) на этом промежутке.
Пример
Исследовать на вып., вогнутость, т. перегиба ф-ию у=х 4 -6х 2 +5. Обл. опред. Х=.
1.найдем у"=4х 3 -12х, у""=12х 2 -12=12(х 2 -1), у""=0, х 2 -1=0, х 1,2 =-т. подозрительные на перегиб, других нет.
Вся обл. опред. разбивается на интервалы (--1),(-1,1),(1, , в каждой из них f ""(х) им. постоянный знак, т.к. непрерывна в них. Легко видеть, что в (--1) +, в (-1,1) -, и в (1, +. Отсюда ясно, что в т. -1 и 1 перегиб, причем в (-1) график функции вогнутый, в (-1,1) выпуклый, в (1, - вогнутый.

ПЛАН ЗАНЯТИЯ № 100
Дисциплина Математика
Специальность
Курс 1 группа C 153
Тема занятия: Наибольшее и наименьшее значение функций
Тип урока: урок закрепления знаний и формирование умений и навыков
Вид занятия: практическое занятие
Цели :
– обучающая: Составить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке. Провести первичное закрепление и первичный контроль усвоения алгоритма;
– развивающая: Развивать логическое мышление, вычислительные навыки;
– воспитательная: содействовать воспитанию у студентов самостоятельности, самопознания, самосозидания и самореализации.
Задачи:
Должен знать: нахождение наибольшего и наименьшего значений функции
Должен уметь: применять полученные знания на практике
Формируемые компетенции :
– общие: ОК 1-9
– профессиональные: ПК 1.1. – ПК 4.3.
Обеспечение занятия: карточки, ОК
Внутридисциплинарные связи: занятие по теме «Наибольшее и наименьшее значения функции» связано с такими темами как: «Определение производной ее геометрический и физический смысл», «Производные основных элементарных функций», «Вторая производная, ее физический смысл», «Нахождение скорости и ускорения с помощью производной», «Дифференцирование сложных функций», «Признак постоянства, возрастание и убывание функции», «Экстремумы функции. Исследование функции на экстремум», «Исследование функции с помощью производной», «Применение производной к построению графиков», «Применение производной к исследованию и построению функций», «Выпуклость графика функции, точки перегиба», «Решение упражнений по теме: «Производная и ее приложение»
Методы обучения: активные: словесные, наглядные
Ход занятия
Организация занятия (3 мин. ).
Сообщение темы и целей занятия. (4 мин .)
Актуализация опорных знаний как переход к освоению новых знаний. (7мин .)
Для изучения новой темы нам необходимо повторить пройденный материал. Сделаете вы это, выполнив устно следующие задания. В тетрадь запишите только ответы к каждому пункту. (3мин.)
По графику функции у=f(x) найдите:
1.Область определения функции.
2. Абсциссы точек, в которых f`(x)=0
3. Абсциссы точек, в которых f`(x) не существует.
4. Наибольшее значение функции. (Унаиб.).
5. Наименьшее значение функции (Унаим.).
Преподаватель: Какие точки называются стационарными?
Обучающийся: Стационарными называются точки, в которых производная функции f / (x)=0.
Преподаватель: Чтобы найти стационарные точки надо: найти производную функции f / (x) и решить уравнение f / (x)=0
Сообщение и усвоение новых знаний с закреплением полученных знаний. (41 мин .)
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у= f (x ) на отрезке [ a ; b ]
найти f "(x);
найти точки, в которых f "(x)=0 или f "(x) не существует, и отобрать из них те, что лежат внутри отрезка ;
вычислить значения функции y=f "(x) в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке , которые можно обозначить так: max y(x) и min y(x).
Пример.
Найдем наибольшее и наименьшее значения функции на отрезке .
Найдем критические точки.
Так как производная функции определена для любого х , решим уравнение
Закрепление нового материала. Решение задач.
1 Вариант.
Найдите У наиб. и У наим. Функции у=2-8x+6 на отрезке[-1;4]
Отбери точки, принадлежащие отрезку [-1;4]
3. Найди у(-1)
2 Вариант.
Найдите У наиб. и У наим. Функции у=+4x-3 на отрезке
Найди стационарные точки, решив уравнение у´=0
Отбери точки, принадлежащие отрезку [-3;2]
3. Найди у(-3)
И в отобранных точках на втором шаге
Отбери среди найденных значений наибольшее и наименьшее.
Решение задания из учебника

Вариант 1. Определите наибольшее и наименьшее значения функции у= х 2 + 4x на отрезке [-3;6].
Варианты ответа:
а) min y(x)= -12, max y(x)= -5; б) min y(x)= -4, max y(x)= 60; в) min y(x)= -12, max y(x)= 4
[-3;6] [-3;6] [-3;6] [-3;6] [-3;6] [-3;6]
Вариант 2. Определите наибольшее и наименьшее значения функции у= х 2 -2х на отрезке .
Варианты ответа:
а) min y(x)= -1, max y(x)= -3/4; б) min y(x)= -1, max y(x)= 8; в) min y(x)= -3/4, max y(x)= -1
Вариант 3. Определите наибольшее и наименьшее значения функции у= 3х 2 + 6x на отрезке [-2;2].
Варианты ответа:
а) min y(x)= -4, max y(x)= 0; б) min y(x)= -20, max y(x)= 0; в) min y(x)= -3, max y(x)= 24
[-2;2] [-2;2] [-2;2] [-2;2] [-2;2] [-2;2]
Вариант 4. Определите наибольшее и наименьшее значения функции у= 2х 2 - 2х на отрезке [-1;3].
Варианты ответа:
а) min y(x)= -0,5, max y(x)= 12; б) min y(x)= 4, max y(x)= 5; в) min y(x)= 0, max y(x)= 5
[-1;3] [-1;3] [-1;3] [-1;3] [-1;3] [-1;3]
Подведение итогов занятия. (5 мин .)
Чем мы занимались сегодня на уроке?
Что понравилось, какие виды деятельности?
Анализ работы студентов, выставление оценок
Рефлексия занятия. (5 мин.)
Продолжите предложения:
Я сегодня узнал…
Мне была интересна задача…
Самая сложная задача для меня заключалась…
Мне занятие понравилось….
Мне занятие не понравилось…
Задание для внеаудиторной самостоятельной работы. (5 мин. )
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования... Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X
, который является или всей областью определения функции или частью области определения. Сам интервал X
может быть отрезком , открытым интервалом ![]() , бесконечным промежутком .
, бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x) .
Навигация по странице.
Наибольшее и наименьшее значение функции - определения, иллюстрации.
Кратко остановимся на основных определениях.
Наибольшим значением функции
![]() , что для любого
, что для любого ![]() справедливо неравенство .
справедливо неравенство .
Наименьшим значением функции
y=f(x)
на промежутке X
называют такое значение ![]() , что для любого
, что для любого ![]() справедливо неравенство .
справедливо неравенство .
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:"Всегда ли можно определить наибольшее (наименьшее) значение функции"? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На отрезке

На первом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .
Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на . В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее - в точке с абсциссой, соответствующей правой границе интервала.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале

На четвертом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри открытого интервала (-6;6) .
На интервале , о наибольшем значении никаких выводов сделать нельзя.
На бесконечности

В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение (min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .
На интервале функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2 справа значения функции стремятся к минус бесконечности (прямая x=2 является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3 . Графическая иллюстрация этого примера приведена на рисунке №8.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке .
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
- Находим область определения функции и проверяем, содержится ли в ней весь отрезок .
- Находим все точки, в которых не существует первая производная и которые содержатся в отрезке (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
- Определяем все стационарные точки, попадающие в отрезок . Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
- Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b .
- Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Пример.
Найти наибольшее и наименьшее значение функции
- на отрезке ;
- на отрезке [-4;-1] .
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.
Находим производную функции по :
Очевидно, производная функции существует во всех точках отрезков и [-4;-1] .
Стационарные точки определим из уравнения . Единственным действительным корнем является x=2 . Эта стационарная точка попадает в первый отрезок .
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1
, x=2
и x=4
:
Следовательно, наибольшее значение функции ![]() достигается при x=1
, а наименьшее значение
достигается при x=1
, а наименьшее значение  – при x=2
.
– при x=2
.
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1]
(так как он не содержит ни одной стационарной точки):