График функции y =f(x) называется выпуклым на интервале (a; b) , если он расположен ниже любой своей касательной на этом интервале.
График функции y =f(x) называется вогнутым на интервале (a; b) , если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c) .
Примеры.

Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема . Пусть y =f(x) дифференцируема на (a; b) . Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ""(x ) < 0, то график функции на этом интервале выпуклый, если же f ""(x ) > 0 – вогнутый.
Доказательство . Предположим для определенности, что f ""(x ) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M 0 с абсциссой x 0 Î (a ; b ) и проведем через точку M 0 касательную. Ее уравнение . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.

Итак, уравнение кривой имеет вид y = f(x) . Обозначим ординату касательной, соответствующую абсциссе x . Тогда . Следовательно, разность ординат кривой и касательной при одном и том же значении x будет .
Разность f(x) – f(x 0) преобразуем по теореме Лагранжа , где c между x и x 0 .
Таким образом,
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: , где c 1 между c 0 и x 0 . По условию теоремы f ""(x ) < 0. Определим знак произведения второго и третьего сомножителей.
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x 0 Î (a ; b ), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Примеры .

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба .
Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.
Теорема . Пусть кривая определяется уравнением y = f(x) . Если f ""(x 0) = 0 или f ""(x 0) не существует и при переходе через значение x = x 0 производная f ""(x ) меняет знак, то точка графика функции с абсциссой x = x 0 есть точка перегиба.
Доказательство . Пусть f ""(x ) < 0 при x < x 0 и f ""(x ) > 0 при x > x 0 . Тогда при x < x 0 кривая выпукла, а при x > x 0 – вогнута. Следовательно, точка A , лежащая на кривой, с абсциссой x 0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ""(x ) > 0 при x < x 0 и f ""(x ) < 0 при x > x 0 .

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.
Примеры. Найти точки перегиба и определить интервалы выпуклости и вогнутости кривых.
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
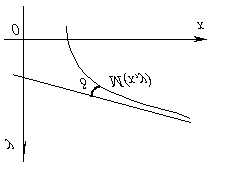

Прямая называется асимптотой графика функции y = f(x) , если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая может приближаться к своей асимптоте, оставаясь с одной стороны от нее или с разных сторон, бесконечное множество раз пересекая асимптоту и переходя с одной ее стороны на другую.
Если обозначим через d расстояние от точки M кривой до асимптоты, то ясно, что d стремится к нулю при удалении точки M в бесконечность.
Будем в дальнейшем различать асимптоты вертикальные и наклонные.
ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ
Пусть при x
→ x 0
с какой-либо стороны функция y
= f(x)
неограниченно возрастает по абсолютной
величине, т.е. или или ![]() . Тогда из определения асимптоты следует, что прямая x
= x 0
является асимптотой. Очевидно и обратное,
если прямая x
= x 0
является асимптотой, т. о. .
. Тогда из определения асимптоты следует, что прямая x
= x 0
является асимптотой. Очевидно и обратное,
если прямая x
= x 0
является асимптотой, т. о. .

Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x → x 0 – 0 или x → x 0 + 0, x = x 0
Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x 0 , при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x 0 .
Примеры.
НАКЛОННЫЕ АСИМПТОТЫ
Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b . Наша задача найти коэффициенты k и b .

Теорема
. Прямая y
= kx
+ b
служит наклонной
асимптотой при x
→ +∞
для графика функции y
= f(x)
тогда и только тогда,
когда ![]() . Аналогичное утверждение верно и при x
→ –∞.
. Аналогичное утверждение верно и при x
→ –∞.
Доказательство . Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию . Обозначим через φ угол наклона асимптоты к оси Ox . Тогда из ΔMNP следует, что . Так как φ постоянный угол (φ ≠ π/2), то , но
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word . Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе .
Правила ввода функций :
Направление выпуклости графика функции. Точки перегиба
Определение : Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.Определение
: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.

Определение : Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x) , характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение:
Точка графика функции y=f(x) , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.

Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x) , в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x) .
- Найти критические точки II рода функции y=f(x) , т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x) . Если при этом критическая точка x 0 разделяет промежутки выпуклости противоположных направлений, то x 0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1
. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x 2 –x 3 .
Решение: Находим f ‘(x) = 12x – 3x 2 , f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0 . x=2 .

f(2) = 6*2 2 – 2 3 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞) ; функция выпукла вниз при x∈(-∞; 2) ; точка перегиба (2;16) .
Пример 2 . Имеет ли точки перегиба функция: f(x)=x 3 -6x 2 +2x-1
Пример 3 . Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x 3 -6x 2 +12x+4
Инструкция
Точки перегиба функции должны принадлежать области ее определения, которую нужно найти в первую очередь. График функции – это линия, которая может быть непрерывной или иметь разрывы, монотонно убывать или возрастать, иметь минимальные или максимальные точки (асимптоты), быть выпуклой или вогнутой. Резкая смена двух последних состояний и называется перегибом.
Необходимое условие существования перегиба функции состоит в равенстве второй нулю. Таким образом, дважды продифференцировав функцию и приравняв получившееся выражение нулю, можно найти абсциссы возможных точек перегиба .
Это условие следует из определения свойств выпуклости и вогнутости графика функции , т.е. отрицательному и положительному значению второй производной. В точке перегиба резкая смена этих свойств, значит, производная переходит нулевую отметку. Однако равенства нулю еще недостаточно для того, чтобы обозначить перегиб.
Существует два достаточных того, что найденная на предыдущем этапе абсцисса принадлежит точке перегиба :Через эту точку можно провести касательную к функции . Вторая производная имеет разные знаки справа и слева от предполагаемой точки перегиба . Таким образом, ее существование в самой точке необязательно, достаточно определить, что в ней она меняет знак.Вторая производная функции равна нулю, а третья – нет.
Решение.Найдите . В данном случае ограничений нет, следовательно, ею является все пространство действительных чисел. Вычислите первую производную:у’ = 3 ∛(х - 5) + (3 х + 3)/∛(х - 5)².
Обратите внимание на . Из него следует, что область определения производной ограничена. Точка х = 5 является выколотой, а значит, через нее может проходить касательная, что отчасти соответствует первому признаку достаточности перегиба .
Определите для получившегося выражения при х → 5 – 0 и х → 5 + 0. Они равны -∞ и +∞. Вы доказали, что через точку х=5 проходит вертикальная касательная. Эта точка может оказаться точкой перегиба , но сначала вычислите вторую производную:У’’ = 1/∛(х - 5)² + 3/∛(х - 5)² – 2/3 (3 х + 3)/∛(х - 5)^5 = (2 х – 22)/∛(х - 5)^5.
Опустите знаменатель, поскольку точку х = 5 вы уже учли. Решите уравнение 2 х – 22 = 0. Оно имеет единственный корень х = 11.Последний этап – подтверждение того, что точки х = 5 и х = 11 являются точками перегиба . Проанализируйте поведение второй производной в их окрестностях. Очевидно, что в точке х = 5 она меняет знак с «+» на «-», а в точке х = 11 – наоборот. Вывод: обе точки являются точками перегиба . Выполнено первое достаточное условие.









