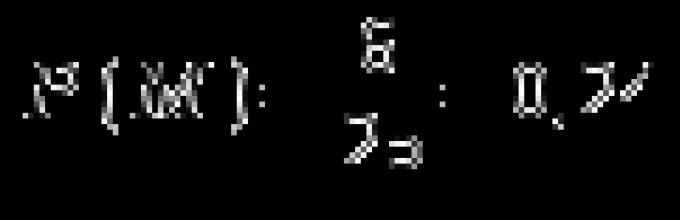Конспект урока
по теме: Случайные события и их вероятности
Цель урока: познакомить студентов с понятиями: события достоверные, невозможные, случайные, абсолютная частота, относительная частота, с классическим определением вероятности, формулой вычисления вероятности событий.
Задачи урока: формирование навыков решения задач на характеристику событий и классическое нахождение вероятности событий; развить у студента умения отличать равновероятные возможности от не равновероятных; воспитание воли, трудолюбия.
Оборудование: мультимедийная доска
Ход урока:
Организационный момент
Актуализация знаний учащихся
О теории вероятности
В повседневной жизни, в практической и научной деятельности часто наблюдаются те или иные явления, проводят определенные эксперименты. В процессе наблюдения или эксперимента приходится встречаться с некоторыми случайными событиями, то есть такими событиями, которые могут произойти или не произойти. Например, поражение мишени или промах при выстреле - случайные события. Выигрыш команды во встрече с соперником, проигрыш или ничейный результат - это тоже случайные события. Закономерности случайных событий изучает специальный раздел математики, который называется теорией вероятностей.
Каждый из нас не отделен от окружающего мира глухой стеной, да и в своей жизни мы ежедневно сталкиваемся с вероятностными ситуациями. Проблема выбора наилучшего из нескольких вариантов решения, оценка степени риска и шансов на успех, представление о справедливости и несправедливости в играх и в реальных жизненных ситуациях - все это, несомненно, находится в сфере реальных интересов личности. Подготовку человека к таким проблемам во всем мире осуществляет школьный курс математики, и в частности ее раздел ""математическая статистика"". Математическая статистика - это раздел математики, который изучает методы обработки и классификации статистических данных для получения научно - обоснованных выводов и принятия решений. В связи с тем, что статистические данные зависят от случайных факторов, математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой.
Еще первобытный вождь понимал, что у десятка охотников вероятность поразить копьем зверя гораздо больше, чем у одного. Поэтому о охотились тогда коллективно. Необоснованно было бы думать. Что такие древние полководцы, как Александр Македонский или Дмитрий Донской, готовясь к сражению, уповали только на доблесть и искусство воинов. Несомненно, они на основании наблюдений и опыта военного руководства умели как-то оценить вероятность своего возвращения со щитом или на щите, знали, когда принимать бой, когда уклониться от него. Они не были рабами случая, но вместе с тем они были еще очень далеки от теории вероятностей. Позднее, с опытом, человек все чаще и чаще стал взвешивать события, классифицировать их исходы как невозможные, возможные и достоверные. Он заметил, что случайность не так уж редко управляют объективные закономерности.
Зарождение теории вероятностей произошло в поисках ответа на вопрос: как часто наступает то или иное событие в большей серии испытаний со случайными исходами, которые происходят в одинаковых условиях.
Изучение нового материала
Событие называется случайным, если при одних и тех же условиях оно может как произойти, так и не произойти
Например, «При подбрасывании игрального кубика выпадет 6 очков»
Говоря о любом случайном событии, мы всегда имеем в виду наличие определенных условий, без которых об этом событии вообще не имеет смысла говорить. Этот комплекс условий называют случайным опытом или случайным экспериментом.
В дальнейшем мы будем называть случайным любое событие, связанное со случайным экспериментом.
Достоверное событие, которое происходят при каждом таком эксперименте.
Невозможное событие, которое никогда не могут произойти.
Предметом теории вероятности является изучение вероятных закономерностей массовых однородных случайных событий.
Рассмотрим несколько примеров случайных экспериментов:
Опыт 1. П одбрасывание монеты. В результате такого эксперимента монета может упасть на одну из двух сторон - «орел» или «решка».
Опыт 2. Подбрасывание кубика. Речь в нем идет об игральном кубике, на гранях которого выбиты точки, символизирующие количество очков от 1 до 6.
Опыт 3. Выбор перчаток. В коробке лежит 3 пары одинаковых перчаток, из нее, не глядя, вытаскивают две перчатки.
Кроме случайного события, с опытом связано еще одно важное понятие - элементарный исход. Исходом (или элементарным исходом, элементарным событием ) называется один из взаимоисключающих друг друга вариантов, которым может завершиться случайный эксперимент.
Определим число возможных исходов в каждом из опытов:
Опыт 1 - 2 исхода: «орел» и «решка»
Опыт 2 - 6 исходов: 1, 2, 3, 4, 5, 6
Сколько исходов в 3-м опыте? (2 исхода: «перчатки на одну рук» и «перчатки на разные руки»)
В опыте 3 можно предложить более детальное описание исходов: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки». А можно - перенумеровать все шесть перчаток и тогда число исходов возрастет до 15.
Неэлементарное событие будет состоять из некоторого множества исходов, которые называются благоприятными для этого события. Благоприятны они в том смысле, что приводят к наступлению данного события.
Определение: Абсолютной частотой случайного события А в серии из n случайных опытов называется число, которое показывает, сколько раз в этой серии произошло событие А
Провели испытания:
Бросили 100 раз игральный кубик. При бросании игрального куба на его верхней грани
кубика выпадает очки:
Исходы испытания: 1. Выпадает одно очко.
2. Выпадает два очка.
3. Выпадает три очка.
4. Выпадает четыре очка.
5. Выпадает пять очков.
6. Выпадает шесть очков.
Случайное событие: - выпадет шесть очков.
Частота события: - в данной серии экспериментов «шестёрка» выпала 17 раз
Относительной частотой - отношение частоты к общему числу испытаний. (в нашем случае )
Т. е. относительной частотой случайного события А в серии из n случайных опытов называется число, которое показывает, какая доля опытов в этой серии завершилась наступлением события А.
Рассмотрим событие В, которое означает выпадение на кубе числа очков, кратного 3. Это событие происходит лишь при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков, т.е. для события В благоприятными являются два исхода из шести равновозможных исходов.
Отношения числа благоприятных исходов к числу всех равновозможных исходов в рассматриваемом примере равно 2/6. Это отношение вероятностью события В и пишут Р(В) = 2/6.
Обозначение Р происходит от французского слова probabilite, что означает «вероятность».
Если все исходы какого-либо испытания равновозможные, то вероятность события в этом испытании равна отношению числа благоприятных для него исходов к числу всех равновозможных исходов.
Задача . Из 25 экзаменационных билетов по геометрии ученик успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?
Решение.
Общее число равновозможных исходов при выборе билетов на экзамене 25. пусть М - событие, заключающееся в том, что ученику достанется на экзамене билет, к которому он не подготовился. Число благоприятных для события М исходов равно 25 - (11 + 8), т. е. 6. Значит,
![]() .
.
Задача. Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередном бросании в сумме выпадет 8 очков, то выигрывает Антон, а если в сумме выпадет 7 очков, то выигрывает Игорь. Можно ли считать, что шансы выиграть в этой игре у мальчиков одинаковы?
Решение. При бросании кубиков на белом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов числа очков, выпавших на черном кубике. Все исходы этого испытания приведены в таблице:
(1; 1)
(2; 1)
(3; 1)
(4; 1)
(5; 1)
(6; 1)
(1; 2)
(2; 2)
(3; 2)
(4; 2)
(5; 2)
(6; 2)
(1; 3)
(2; 3)
(3; 3)
(4; 3)
(5; 3)
(6; 3)
(1; 4)
(2; 4)
(3; 4)
(4; 4)
(5; 4)
(6; 4)
(1; 5)
(2; 5)
(3; 5)
(4; 5)
(5; 5)
(6; 5)
(1; 6)
(2; 6)
(3; 6)
(4; 6)
(5; 6)
(6; 6)
В каждой паре на первом месте записано число очков, выпавших на белом кубике, а на втором месте - число очков, выпавших на черном кубике. Указанные исходы испытания равновозможны. Общее число равновозможных исходов равно 36. Пусть событие А означает, что при бросании кубиков в сумме выпало 8 очков, а событие В означает, что в сумме выпало 7 очков.
Для события А благоприятными являются 5 исходов: (2; 6), (3; 5), (4; 4), (5; 3), (6; 2).
Для события В благоприятными являются 6 исходов:
(1; 6), (2; 5), (3; 4), (4; 3), (5; 2), (6; 1).
Отсюда , .
Поэтому шансов выиграть у Игоря больше, чем у Антона.
Закрепление нового материала.
Решить следующие задачи:
Для новогодней лотереи отпечатали 1500 билетов, из которых 120 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным?
Какова вероятность того, что при бросании игрального кубика выпадет 1 очко? более 3 очков?
Ученик записал в тетради произвольно двузначное число. Какова вероятность того, что сумма цифр этого числа окажется равной 6?
В коробке лежит 10 шаров, из них 5 черных, 2 белых, остальные – красные. Какова вероятность вытащить черный шар? вытащить не красный шар?
Андрей и Олег договорились, что если при бросании двух игральных кубиков в сумме выпадет число очков кратное 5, то выигрывает Андрей, а если в сумме выпадет число очков, кратное 6, то выигрывает Олег. Справедлива ли эта игра? У кого из мальчиков больше шансов выиграть? Какова вероятность выигрыша каждого мальчика?
5. Итоги урока.
6. Домашнее задание.
Задача 1. В урне находятся 3 синих, 8 красных и 9 белых шаров одинакового размера и веса, неразличимых на ощупь. Шары тщательно перемешаны. Какова вероятность появления синего, красного и белого шаров при одном вынимании шара из урны?
Задача 2. Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а Лена – билет, который участвует в розыгрыше трех призов на 70000. У кого больше шансов выиграть?
Если вас интересует вопрос заголовка, вы наверняка студент или школьник, столкнувшийся с новым для себя предметом. Задачи теории вероятностей сейчас решают и школьники пятых классов продвинутых школ, и старшеклассники перед ЕГЭ, и студенты буквально всех специальностей — от географов до математиков. Что же это за предмет такой, и как к нему подойти?
Вероятность. Что это?
Теория вероятностей , как следует из названия, имеет дело с вероятностями. Нас окружают множество вещей и явлений, о которых, как бы ни была развита наука, нельзя сделать точных прогнозов. Мы не знаем, какую карту вытянем из колоды наугад или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, можем строить прогнозы и вычислять вероятности этих случайных событий.
Таким образом, мы сталкиваемся с основным понятием случайного события — явления, поведение которого невозможно предсказать, опыта, результат которого заранее невозможно вычислить и т.п. Именно вероятности событий вычисляются в типовых задачах. Вероятность — это некоторая, строго говоря, функция, принимающая значения от 0 до 1 и характеризующая данное случайное событие. 0 — событие практически невозможно, 1 — событие практически достоверно, 0,5 (или «50 на 50») — с равной вероятностью событие произойдет или нет.
Алгоритм решения типовых задач на нахождение вероятности
Подробнее с основами теории вероятностей можно ознакомиться, например, в онлайн учебнике. А теперь не будем ходить вокруг да около, и сформулируем примерную схему , по которой следует решать стандартные учебные задачи на вычисление вероятности случайного события, а затем ниже на примерах проиллюстрируем ее применение.
- Внимательно прочитать задачу и понять, что именно происходит (что из какого ящика вытаскивается, что где лежало, сколько приборов работает и т.п.)
- Найти основной вопрос задачи вроде «вычислить вероятность того, что …» и вот это многоточие записать в виде события, вероятность которого надо найти.
- Событие записано. Теперь надо понять, к какой «схеме» теории вероятностей относится задача, чтобы правильно выбрать формулы для решения.
Вероятность
Ответьте на тестовые вопросы типа:
- происходит одно испытание (например, выбрасывание двух костей) или несколько (например, проверка 10 приборов);
- если испытаний несколько, зависимы ли результаты одного от других (зависимость или независимость событий);
- событие происходит в единственной ситуации или задача говорит о нескольких возможных гипотезах (например, шар вынимается из любого ящика из трех, или из конкретного).
Чем больше опыт решения задач, тем легче будет определить, какие формулы подходят.
- Выбрана формула (или несколько) для решения. Записываем все данные задачи и подставляем в данную формулу.
- Вуаля, вероятность найдена.
Готовые решения задач по любым разделам теории вероятностей, более 10000 примеров! Найди свою задачу:
Как решать задачи: классическая вероятность
Пример 1. В группе из 30 студентов на контрольной работе 6 студентов получили «5», 10 студентов – «4», 9 студентов – «3», остальные – «2». Найти вероятность того, что 3 студента, вызванные к доске, получили по контрольной работе «2».
Начинаем решение по пунктам, описанным выше.
- В задаче речь идет о выборе 3 студентов из группы, которые удовлетворяют определенным условиям.
- Вводим основное событие $X$ = (Все 3 студента, вызванные к доске, получили по контрольной работе «2»).
- Так как в задаче происходит только одно испытание и оно связано с отбором/выбором по определенному условию, речь идет о классическом определении вероятности. Запишем формулу: $P=m/n$, где $m$ – число исходов, благоприятствующих осуществлению события $X$, а $n$ – число всех равновозможных элементарных исходов.
- Теперь необходимо найти значения $m$ и $n$ для этой задачи. Сначала найдем число всех возможных исходов — число способов выбрать 3 студентов из 30. Так как порядок выбора не имеет значения, это число сочетаний из 30 по 3: $$n=C_{30}^3=\frac{30!}{3!27!}=\frac{28\cdot 29 \cdot 30}{1\cdot 2 \cdot 3}=4060.$$ Найдем число способов вызвать только студентов, получивших «2». Всего таких студентов было $30-6-10-9=5$ человек, поэтому $$m=C_{5}^3=\frac{5!}{3!2!}=\frac{4 \cdot 5}{1\cdot 2}=10.$$
- Получаем вероятность: $$P(X)=\frac{m}{n}=\frac{10}{4060}=0,002.$$ Задача решена.
Еще примеры: Решенные задачи на классическое определение вероятности.
Как решать задачи: формула Бернулли
Пример 2. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз?
Снова по схеме решения задач на вероятность рассматриваем данную задачу:
- В задаче идет речь о серии одинаковых испытаний — бросаний монеты.
- Вводим основное событие $X$ = (При 8 бросаниях монеты герб выпадет 5 раз).
- Так как в задаче происходит несколько испытаний, и вероятность появления события (герба) одинакова в каждом испытании, речь идет о схеме Бернулли. Запишем формулу Бернулли, которая описывает вероятность того, что из $n$ бросков монет герб выпадет ровно $k$ раз: $$ P_{n}(k)=C_n^k \cdot p^k \cdot (1-p)^{n-k}.$$
- Записываем данные из условия задачи: $n=8, p=0,5$ (вероятность выпадения герба в каждом броске равна 0,5) и $k=5$
- Подставляем и получаем вероятность: $$ P(X)=P_{8}(5)=C_8^5 \cdot 0,5^5 \cdot (1-0,5)^{8-5}=\frac{8!}{5!3!}\cdot 0,5^8=\frac{6\cdot 7 \cdot 8}{1\cdot 2 \cdot 3} \cdot 0,5^8= 0,219.$$ Задача решена.
Еще примеры: Решенные задачи на формулу Бернулли, решебник задач по теории вероятности.
И это все? Конечно, нет.
Выше мы упомянули только малую часть тем и формул теории вероятностей, для более подробного изучения вы можете посмотреть учебник онлайн на данном сайте (или скачать классические учебники по ТВ), ознакомиться со статьями по решению вероятностных задач, бесплатными примерами, воспользоваться онлайн калькуляторами. Удачи!
Спасибо, что читаете и делитесь с другими
Другие полезные статьи по теории вероятностей
Статьи о решении математических задач
Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием . Результат, исход испытания называется событием .
Пример 1 . Сдача экзамена — это испытание; получение определенной отметки — событие. Выстрел — это испытание; попадание в определенную область мишени — событие. Бросание игрального кубика — это испытание; появление того или иного числа очков на брошенной игральной кости — событие.
Виды случайных событий
События называются несовместными , если появление одного из них исключает появления других событий в одном и том же испытании.
Пример 2 :
- несовместные события : день и ночь, человек читает и человек спит, число иррациональное и четное;
- совместные события : идет дождь и идет снег, человек ест и человек читает, число целое и четное.
Несколько событий образуют полную группу (пространство исходов) , если в результате испытания появиться хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие.
Пример 3 .
Урок алгебры » Случайные события. Вероятность случайного события.»
При сдаче зачета возможны следующие исходы: «зачтено», «не зачтено», «не явился»; при подбрасывании монеты – «орел», «решка».
Пример 4 . Пусть в урне содержится 6 одинаковых шаров, причем 2 из них — красные, 3 — синие и 1 — белый. Какова возможность вынуть наудачу из урны цветной шар? Можно ли охарактеризовать эту возможность числом?
Оказывается можно. Это число и называется вероятностью события А (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события .
Каждый из возможных результатов испытания (в примере 4, испытание состоит в извлечении шара из урны) называется элементарным исходом .
Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. В примере 4 благоприятствуют событию А (появление цветного шара) 5 исходов.
События называются равновозможными , если есть основания считать, что не одно из них не является более возможным, чем другое.
Пример 5 . Появление того или иного числа очков на брошенном игральном кубике – равновозможные события.
Вероятностью P(A) события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Вероятность P(A) события А определяется по формуле
где m – число элементарных исходов, благоприятствующих A ; n – число всех возможных элементарных исходов испытания.
В примере 4 всего элементарных исходов 6 ; из них 5 благоприятствуют событию А . Следовательно, вероятность того что взятый шар окажется цветным, равна P(A) = 5/6 .
Пример 6 . Определить вероятность выпадения нечётного числа очков на кости.
Решение. При бросании кости событие A – «выпало нечётное число очков» можно записать как подмножество {1, 3, 5} пространства исходов {1, 2, 3, 4, 5, 6} (рис. 1).

Число всех равновозможных исходов n = 6, а число благоприятных событию A – m = 3. Следовательно,

Пример 7 . В урне находится 7 шаров: 2 белых, 4 черных и 1 красный. Вынимается один шар наугад. Какова вероятность того, что вынутый шар будет чёрным?
Решение. Занумеруем шары. Пусть, например, шары с номерами 1 и 2 – белые, с номерами 3, 4, 5 и 6 – чёрные, а красному шару присвоим номер 7 .
Так как мы можем вынуть только один из семи шаров, то общее число равновозможных исходов равно семи (n = 7 ). Из них 4 исхода – появление шаров с номерами 3, 4, 5 и 6 – приведут к тому, что вынутый шар будет чёрным (m = 4 ). Тем самым, вероятность события А , состоящего в появлении чёрного шара, равна
Вычислите вероятность того, что вынутый шар будет белым.
Пример 8 .
Вычислить вероятность выпадения в сумме 10 очков при бросании пары костей.
Решение.
Рассмотрим все равновозможные исходы в результате бросания двух костей (их число равно 36
— рекомендуем записать в виде таблицы). Выпадение в сумме 10
очков (событие А
) возможно в трёх случаях – 4
очка на первой кости и 6
на второй, 5
очков на первой и 5
на второй, 6
очков на первой и 4
на второй. Поэтому вероятность события А (выпадения в сумме 10
очков) равна 
Свойство 1 . Вероятность достоверного события А равна единице: Р(А) = 1 .
Свойство 2 . Вероятность невозможного события А равна нулю: Р(А) = 0 .
Свойство 3 . Вероятность случайного события есть положительное число, заключенное между нулем и единицей :
0 £ P (A) £ 1.
Пример 9 . Так как вероятность выпадения 13 очков при бросании пары костей – невозможное событие, его вероятность равна нулю .
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно. Кроме этого, часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. По этой причине, наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение .
Статистическое определение вероятности
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.
Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
где m – число появлений события А , n – общее число испытаний.
Классическая вероятность вычисляется до опыта, а относительная частота – после опыта .
Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости .
Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.
Таким образом, при достаточно большом количестве испытаний в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
Пример 10
. Естествоиспытатель К. Пирсон терпеливо подбрасывал монету и после каждого бросания не ленился записывать полученный результат. Проделав эту операцию 24 000 раз, он обнаружил, что герб выпадал в 12 012 случаях. Вычисляя относительную частоту выпадения герба, он получил  , что практически равно 1/2.
, что практически равно 1/2.
Многих интересует вопрос: возможно ли повлиять на случайные события, выявить какую-либо закономерность событий, получить тот результат, который желателен. Все явления, которые окружают нас, происходят и изменяются с какой-то долей случайности, неопределенности.
Со случайными событиями мы встречаемся чаще, чем это принято считать. Случайные факторы лежат в основе окружающей среды, экономики, политики, социальной и общественной жизни, они определяют течение любого процесса массового обслуживания - торговли, телефонной связи, транспортных услуг и медицинской помощи. Задача управления различного рода процессами, которая наиболее остро стоит перед современным обществом, состоит в том, чтобы научиться ориентироваться в мире случайностей и активно действовать, опираясь на скрытые специфические закономерности.
Все явления окружающей нас действительности можно рассматривать с точки зрения вероятности их наступления. Когда студент идет на экзамен, вероятность получения им хорошей оценки зависит от нескольких причин: подготовленности студента, удачно выбранного билета, самочувствия, настроя.
Экономиста может интересовать вероятность того, что цены на товар не вырастут, если не снизится объем его производства, или вероятность того, что застрахованный автомобиль не попадет в аварию.
Все эти события являются случайными и могут наступить или нет с некоторой долей неопределенности. Количественной мерой такой неопределенности является вероятность наступления случайного события, под которой понимают число, которое выражает степень уверенности в наступлении того или иного случайного события.
Случайными событиями называют возможные результаты единичной операции, или испытания .
Под испытанием следует понимать процесс, включающий в себя определенные условия и приводящий к одному из нескольких возможных исходов .
Например: испытание - бросание монеты, случайное событие - выпадение герба. Испытание - рождение ребенка, случайное событие - пол ребенка - мужской.
Исходом опыта может быть результат наблюдения, измерения, оценки.
Случайное событие может состоять из нескольких элементарных событий.
Единичный, отдельный исход испытания называется элементарным событием.
Событие называется случайным, если в результате испытания (опыта) оно может произойти, а может и не произойти.
Например, стрелок, производящий выстрел, может попасть или не попасть в цель. В этом случае испытание - это выстрел, а возможные элементарные исходы - попадание или непопадание в цель. Футбольная команда может участвовать в матче - это испытание, в результате которого могут наступить исходы, или элементарные события: выигрыш, проигрыш или ничья.
Оценка студента на экзамене - это случайное событие, которое состоит из элементарных событий: получение оценки «отлично», получение оценки «хорошо», получение оценки «удовлетворительно», получение оценки «неудовлетворительно».
Элементарные события можно классифицировать по мере их неопределенности как достоверные, невозможные и случайные.
Достовернымназывают событие, которое обязательно произойдет при определенном комплексе условий .
Например, если в ящике находятся только стандартные детали, то извлечение из него стандартной детали есть событие достоверное. Достоверным является и то, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Событие, которое не может произойти в результате данного испытания, называется невозможным .
Если в ящике все детали стандартные, то извлечение из него нестандартной детали есть событие невозможное. Квадрат вещественного числа не может быть отрицательным. Достоверные и невозможные события, вообще говоря, не являются случайными.
Случайные события. Вероятность (стр. 1)
Фундаментом для научного подхода к поиску ответов на вопросы подобного рода является теория вероятностей.
Зарождение теории вероятностей и формирование первых понятий этой ветви математики произошло в середине 17 века, когда Паскаль, Ферма, Бернулли попытались осуществить анализ задач связанных с азартными играми новыми методами. Скоро стало ясно, что возникающая теория найдет широкий круг применения для решения многих задач возникающих в различных сферах деятельности человека .
Производя достаточно большое количество опытов или испытаний, можно определить, как часто появляется событие, и вычислить вероятность его наступления. Вероятность, определенную таким образом, называют статистической или послеопытной. В некоторых случаях можно определить доопытную вероятность, которую называют классической.
Вероятностью появления события А называют отношение числа исходов, благоприятствующих появлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов. Обозначим число благоприятствующих событию А исходов через М, а число всех возможных исходов N. тогда для определения вероятности можно использовать формулу Р (А) = М/N .
Я провела эксперимент: попробовала вытащить из 15 шариков, 2 из которых красные, остальные зеленые, произвольным образом 2 шарика. Пыталась определить вероятность того, что оба шарика окажутся красными; оба шарика будут зелеными; один шарик будет красный, другой зеленый.
Предположенный перед проведением эксперимента результат оправдался: наиболее возможным исходом является вытаскивание 2 зеленых шариков, наименее возможным исходом является вытаскивание 2 красных шариков.
При сравнении практической и теоретической вероятности, обнаружилось довольно большое расхождение, причиной которого является малое количество проведенных испытаний.
Для получения более точного результата желательно проводить как можно больше испытаний, рассматривать всевозможные исходы испытаний и благоприятные исходы. Не забывать, что проверить это всегда можно и теоретически. При этом вероятности до проведения опыта и после проведения должны совпадать.
Проведя исследование по данному вопросу, я пришла к выводу: теория вероятности не влияет на случайные события, она только позволяет выяснить степень его наступления, а вероятность, посчитанная во время эксперимента, тем точнее, чем больше проведено испытаний.
Литература:
- Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами / А. И. Кибзун. - М.: Физматлит, 2002. - 224 с.
- Кочетков Е. С., Смерчинская С. О., Соколов В. В. Теория вероятностей и математическая статистика. - М.: ФОРУМ: ИНФРА-М, 2006. - 240 с.
- Письменный Д. Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. - М.: Айрис-пресс, 2007. - 288 с.
Спасибо, что читаете и делитесь с другими
Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным , если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу , если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события $А$, если появление этого события влечет за собой появление события $А$.
Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8).
Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара.
Вероятностью события $A$ называют отношение числа $m$ благоприятствующих этому событию исходов к общему числу $n$ всех равновозможных несовместных элементарных исходов, образующих полную группу $$P(A)=\frac{m}{n}. \quad(1)$$
Свойство 1.
Вероятность достоверного события равна единице
Свойство 2.
Вероятность невозможного события равна нулю.
Свойство 3.
Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству $0 \le P(A) \le 1$ .
Онлайн-калькуляторы
Большой пласт задач, решаемых с помощью формулы (1) относится к теме гипергеометрической вероятности. Ниже по ссылкам вы можете найти описание популярных задач и онлайн-калькуляторы для их решений:
- Задача про шары (в урне находится $k$ белых и $n$ черных шаров, вынимают $m$ шаров…)
- Задача про детали (в ящике находится $k$ стандартных и $n$ бракованных деталей, вынимают $m$ деталей…)
- Задача про лотерейные билеты (в лотерее участвуют $k$ выигрышных и $n$ безвыигрышных билета, куплено $m$ билетов…)
Примеры решений задач на классическую вероятность
Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m =n =10. Следовательно, Р (А )=1. Событие А достоверное .. Количество элементарных исходов (количество карт)
Искомая вероятность  .
.
Формулы по теории вероятности онлайн
В данном разделе вы найдете формулы по теории вероятностей в онлайн-варианте (скачать можно на странице Таблицы и формулы по теории вероятностей). Если слово подчеркнуто, щелкнув на ссылке, вы перейдете к подробному описанию термина, примерам или вычислению на онлайн-калькуляторе. Используйте эти возможности!
А также для изучения тервера у нас есть:
Спасибо, что читаете и делитесь с другими
I. Случайные события. Основные формулы онлайн
1. Основные формулы комбинаторики
Число перестановок $$P_n = n!
Учебник по теории вероятностей
1\cdot 2 \cdot 3 \cdot … \cdot (n-1) \cdot n$$
Число размещений $$A_m^n = n \cdot (n-1) \cdot … \cdot (n-m+1)$$
Число сочетаний $$C_n^m =\frac{A_n^m}{P_m}=\frac{n!}{m! \cdot (n-m)!}$$
2. Классическое определение вероятности
$$P(A) = \frac{m}{n},$$ где $m$ — число благоприятствующих событию $A$ исходов, $n$ — число всех элементарных равновозможных исходов.
Подробнее о классической вероятности см. в онлайн-учебнике и калькуляторах решений.
3. Вероятность суммы событий
Теорема сложения вероятностей несовместных событий:
$$ P(A+B) = P(A)+P(B) $$
Теорема сложения вероятностей совместных событий:
$$ P(A+B) = P(A)+P(B)-P(AB) $$
Примеры решений и теория по алгебре событий тут.
4. Вероятность произведения событий
Теорема умножения вероятностей независимых событий:
$$ P(A\cdot B) =P(A)\cdot P(B) $$
Теорема умножения вероятностей зависимых событий:
$$ P(A\cdot B) =P(A)\cdot P(B|A),\\ P(A\cdot B) =P(B)\cdot P(A|B). $$
$P(A|B)$ — условная вероятность события $A$ при условии, что произошло событие $B$,
$P(B|A)$ — условная вероятность события $B$ при условии, что произошло событие $A$.
Подробнее об условной вероятности.
5. Формула полной вероятности
$$ P(A)=\sum_{k=1}^{n} P(H_k)\cdot P(A|H_k), $$
6. Формула Байеса (Бейеса). Вычисление апостериорных вероятностей гипотез
$$ P(H_m|A) =\frac{P(H_m)\cdot P(A|H_m)}{P(A)} = \frac{P(H_m)\cdot P(A|H_m)}{\sum\limits_{k=1}^{n} P(H_k)\cdot P(A|H_k)}, $$
где $H_1, H_2, …, H_n$ — полная группа гипотез.
Примеры и теория на эту тему.
7. Формула Бернулли
$$ P_n(k)=C_n^k \cdot p^k \cdot (1-p)^{n-k} = \frac{n!}{k! \cdot (n-k)!}\cdot p^k \cdot (1-p)^{n-k} $$ вероятность появления события ровно $k$ раз в $n$ независимых испытаниях, $p$ — вероятность появления события при одном испытании.
Еще полезное по формуле Бернулли теория и примеры, онлайн-калькуляторы.
8. Наивероятнейшее число наступления события
Наивероятнейшее число $k_0$ появления события при $n$ независимых испытаниях (где $p$ — вероятность появления события при одном испытании):
$$ np-(1-p) \le k_0 \le np+p. $$
Вычислить наивероятнейшее значение онлайн.
9. Локальная формула Лапласа
$$ P_n(k) = \frac{1}{\sqrt{npq}} \varphi\left(\frac{k-np}{\sqrt{npq}} \right) $$
вероятность появления события ровно $k$ раз при $n$ независимых испытаниях, $p$ — вероятность появления события при одном испытании, $q=1-p$.
Значения функции $\varphi(x)$ берутся из таблицы.
10. Интегральная формула Лапласа
$$ P_n(m_1, m_2) = \Phi\left(\frac{m_2-np}{\sqrt{npq}} \right)-\Phi\left(\frac{m_1-np}{\sqrt{npq}} \right) $$
вероятность появления события не менее $m_1$ и не более $m_2$ раз при $n$ независимых испытаниях, $p$ — вероятность появления события при одном испытании, $q=1-p$.
Значения функции $\Phi(x)$ берутся из таблицы.
Теория и примеры на формулы Муавра-Лапласа.
11. Оценка отклонения относительной частоты от постоянной вероятности $p$
$$ P\left(\left| \frac{m}{n} -p\right| \le \varepsilon\right) = 2 \Phi\left(\varepsilon\cdot \frac{n}{\sqrt{p(1-p)}} \right) $$
$\varepsilon$ — величина отклонения, $p$ — вероятность появления события.
Решенные задачи по теории вероятностей
Нужна готовая задача по терверу? Найдите на сайте-решебнике:
Каталог формул по теории вероятности онлайн
Полный список страниц с формулами:
Спасибо, что читаете и делитесь с другими
Учебник по теории вероятности: содержание
Глава 1. Случайные события. Вычисление вероятности
1.1. Элементы комбинаторики
1.2. Классическое определение вероятности
1.3. Геометрическое определение вероятности
1.4. Сложение и умножение вероятностей
1.5. Условная вероятность
1.6. Формула полной вероятности и формула Байеса
1.7. Независимые испытания. Формула Бернулли
1.8. Наивероятнейшее число успехов
1.9. Формула Пуассона
1.10. Теоремы Муавра-Лапласа
1.1. Элементы комбинаторики
Рассмотрим некоторое множество Х , состоящее из n элементов . Будем выбирать из этого множества различные упорядоченные подмножества из k элементов.
Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х .
Если выбор элементов множества из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле (размещения с повторениями ).
Если
же выбор делается без возвращения, т.е.
каждый элемент множества Х
можно
выбирать только один раз, то количество
размещений из n
по k
обозначается и
определяется равенством
(размещения без повторений ).
Пример.
Пусть
даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить
сколько трехзначных чисел можно составить
из этих цифр.
Решение.
Если
цифры могут повторяться, то количество
трехзначных чисел будет ![]() .
Если цифры не повторяются, то
.
Если цифры не повторяются, то ![]() .
.
Пример. Студенты института изучают в каждом семестре по десять дисциплин. В расписание занятий включаются каждый день по 3 дисциплины. Сколько различных расписаний может составить диспетчерская?
Решение
.
Расписание на каждый день может отличаться
либо предметами, либо порядком расположения
этих предметов, поэтому имеем размещения: ![]()
Частный
случай размещения
при n
=k
называется перестановкой
из n
элементов.
Число всех перестановок из n
элементов
равно
.
Пример . 30 книг стоит на книжной полке, из них 27 различных книг и одного автора три книги. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом?
Решение. Будем считать три книги одного автора за одну книгу, тогда число перестановок будет . А три книги можно переставлять между собой способами, тогда по правилу произведения имеем, что искомое число способов равно: *=3!*28!
Пусть
теперь из множества Х
выбирается
неупорядоченное подмножество (порядок
элементов в подмножестве не имеет
значения). Сочетаниями
из n
элементов
по k
называются
подмножества из k
элементов,
отличающиеся друг от друга хотя бы одним
элементом. Общее число всех сочетаний
из n
по k
обозначается и
равно![]() .
.
Справедливы равенства: , , .
Пример. В группе из 27 студентов нужно выбрать трех дежурных. Сколькими способами можно это сделать?
Решение.
Так
как порядок студентов не важен, используем
формулу для числа сочетаний: ![]() .
.
При решении задач комбинаторики используют следующие правила:
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.
Пример. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка?
Решение. Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами выбор туфель. По принципу умножения получается 4*5*3=60 нарядов (комбинаций).
1.2. Классическое определение вероятности
Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным , если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу , если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А , если появление этого события влечет за собой появление события А .
Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара.
Вероятностью
события
A
называют
отношение числа m благоприятствующих
этому событию исходов к общему числу n
всех равновозможных несовместных
элементарных исходов, образующих полную
группу
Свойство
1.
Вероятность
достоверного события равна единице
Свойство
2.
Вероятность
невозможного события равна нулю.
Свойство
3.
Вероятность
случайного события есть положительное
число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству .
Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаевm =n =10. Следовательно, Р (А )=1. Событие А достоверное .
Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?
Решение.
Вынуть
два шара из десяти можно следующим
числом способов: ![]() .
.
Число
случаев, когда среди этих двух шаров
будут два белых, равно ![]() .
.
Искомая
вероятность ![]() .
.
Пример. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?
Решение. Так как синих шаров в урне нет, то m =0, n =15. Следовательно, искомая вероятность р =0. Событие, заключающееся в вынимании синего шара, невозможное .
Пример. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?
Решение
.
Количество элементарных исходов
(количество карт) n
=36.
Событие А
=
(Появление карты червовой масти). Число
случаев, благоприятствующих появлению
события А
, m
=9.
Следовательно,![]() .
.
Пример. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.
Решение.
Общее
число возможных исходов равно числу
способов, которыми можно отобрать 7
человек из 10, т.е. ![]() .
.
Найдем
число исходов, благоприятствующих
интересующему нас событию: трех женщин
можно выбрать из четырех способами;
при этом остальные четыре человека
должны быть мужчинами, их можно
отобрать способами.
Следовательно, число благоприятствующих
исходов равно ![]() .
.
Искомая
вероятность  .
.
1.3. Геометрическое определение вероятности
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая
вероятность
события
А определяется отношением:
,
где
m(G), m(A) – геометрические меры (длины,
площади или объемы) всего пространства
элементарных исходов и события А.
Пример. На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r (). Найти вероятность того, что круг пересечет некоторую полосу.
Решение.
В
качестве элементарного исхода этого
испытания будем считать расстояние x
от
центра круга до осевой линии ближайшей
к кругу полосы. Тогда все пространство
элементарных исходов – это отрезок ![]() .
Пересечение круга с полосой произойдет
в том случае, если его центр попадет в
полосу, т.е. ,
или будет находится от края полосы на
расстоянии меньшем чем радиус, т.е. .
.
Пересечение круга с полосой произойдет
в том случае, если его центр попадет в
полосу, т.е. ,
или будет находится от края полосы на
расстоянии меньшем чем радиус, т.е. .
Для искомой вероятности получаем: .
1.4. Сложение и умножение вероятностей
Событие А называется частным случаем события В , если при наступлении А наступает и В . То, что А является частным случаем В , записываем .
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В .
Суммой событий А и В называется событие А + В , которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двухнесовместных событий равна сумме вероятностей этих событий.
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
![]() .
.
Если случайные события образуют полную группу несовместных событий, то имеет место равенство
Произведением событий А и В называется событие АВ , которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными , если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
События событий А и В называются независимыми , если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В , если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности (см. следующий раздел).
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение.
Обозначим
события: А
–
вынули белый шар из первого ящика,
;
Вынули черный шар из первого ящика,
;
В
–
белый шар из второго ящика,
;
Черный шар из второго ящика,
.
Нам
нужно, чтобы произошло одно из
событий или .
По теореме об умножении вероятностей
, .
Тогда
искомая вероятность по теореме сложения
будет
.
Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка, ;
В – попадание второго стрелка, .
Тогда -
промах первого, ![]() ;
;
Промах второго, ![]() .
.
Найдем нужные вероятности.
а) АВ – двойное попадание,
б) – двойной промах, .
в) А +В – хотя бы одно попадание,
г) – одно попадание,
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Если события имеют одинаковую вероятность , то формула принимает простой вид:
![]() .
.
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p 1 = 0,8;p 2 = 0,7; p 3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события (попадание первого орудия), (попадание второго орудия) и (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям , и (т. е. вероятности промахов), соответственно равны:
![]() ,
, ![]() ,
, ![]()
Искомая вероятность .
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События "машина работает" и "машина не работает" (в данный момент) - противоположные, поэтому сумма их вероятностей равна единице:
Отсюда вероятность того, что машина в данный момент не работает, равна
Искомая вероятность
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула .
Приняв
во внимание, что, по условию, ![]() (следовательно, ),
получим
(следовательно, ),
получим
Прологарифмируем это неравенство по основанию 10:

Итак, , т.е. стрелок должен произвести не менее 5 выстрелов.
1.5. Условная вероятность
Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной ; если же налагаются и другие дополнительные условия, то вероятность события называют условной . Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А .
Условной
вероятностью
![]() (два
обозначения) называют вероятность
события В
,
вычисленную в предположении, что
событие А
уже
наступило.
(два
обозначения) называют вероятность
события В
,
вычисленную в предположении, что
событие А
уже
наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
В
частности, отсюда получаем ![]() .
.
Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.
Решение.
Очевидно,
что вероятность события А
,
если событие В
произошло,
будет ![]() .
.
Вероятность
события А
при
условии, что событие В
не
произошло, будет
.
Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение . После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность .
Этот
же результат можно получить по формуле
.
Действительно,
вероятность появления белого шара при
первом испытании
.
Найдем
вероятность того,
что в первом испытании появится черный
шар, а во втором - белый. Общее число
исходов - совместного появления двух
шаров, безразлично какого цвета, равно
числу размещений .
Из этого числа исходов
событию благоприятствуют исходов.
Следовательно, ![]() .
.
Искомая
условная вероятность ![]()
Результаты совпали.
Пример. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?
Решение . Пусть А - событие, состоящее в том, что на линию вышел трамвай маршрута №1, В - маршрута №2.
Рассмотрим
все события, которые могут при этом быть
(в условиях нашей задачи): ![]() .
Из них нас будут интересовать только
первое и третье, когда вторым выйдет
трамвай маршрута №1.
.
Из них нас будут интересовать только
первое и третье, когда вторым выйдет
трамвай маршрута №1.
Так как все эти события совместны, то:
![]() ;
;
![]() ;
;
отсюда
искомая вероятность
Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?
Решение . Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А - появление первой карты такой масти, В - появление второй карты той же масти. Событие В зависит от события А , т.к. его вероятность меняется от того, произошло или нет событие А . Поэтому придется воспользоваться теоремой умножения в ее общей форме:
![]() ,
,
где ![]() (после
вынимания первой карты осталось 35 карт,
из них той же масти, что и первая - 8).
(после
вынимания первой карты осталось 35 карт,
из них той же масти, что и первая - 8).
Получаем
.
События,
состоящие в том, что будут вынуты две
карты масти «пики», масти «треф» и т.д.,
несовместны друг с другом. Следовательно,
для нахождения вероятности их объединения
воспользуемся теоремой сложения:![]() .
.
1.6. Формула полной вероятности и формула Байеса
Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий , то вероятность события А вычисляется по формуле
Эта формула называется формулой полной вероятности .
Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами . Тогда по формуле полной вероятности
Если событие А произошло, то это может изменить вероятности гипотез .
По теореме умножения вероятностей
![]() .
.
Аналогично, для остальных гипотез
![]()
Полученная формула называется формулой Байеса (формулой Бейеса ). Вероятности гипотез называются апостериорными вероятностями , тогда как -априорными вероятностями .
Пример. В магаз поступила новая продукция с 3х предприятий.20%-продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
А 1 - на линию огня вызван первый стрелок,
А 2 - на линию огня вызван второй стрелок,
А 1 - на линию огня вызван третий стрелок.
Так
как вызов на линию огня любого стрелка
равновозможен, то ![]()
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

по формуле Байеса находим вероятность гипотезы после опыта:
Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.
а) Каков процент брака на конвейере?
б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?
Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – взятая наудачу деталь обработана на -ом станке, .
Условные вероятности (в условии задачи они даны в форме процентов):
Зависимости между производительностями станков означают следующее:
А так как гипотезы образуют полную группу, то .
Решив полученную систему уравнений, найдем: .
а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.
б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
1.7. Независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли .
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак,
пусть в результате испытания возможны два
исхода
:
либо появится событие А
,
либо противоположное ему событие.
Проведем n испытаний Бернулли. Это
означает, что все n испытаний независимы;
вероятность появления события А
в
каждом отдельно взятом или единичном
испытании постоянна и от испытания к
испытанию не изменяется (т.е. испытания
проводятся в одинаковых условиях).
Обозначим вероятность появления
события А
в
единичном испытании буквой р, т.е. ,
а вероятность противоположного события
(событие А
не
наступило) - буквой ![]() .
.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражаетсяформулой Бернулли
Распределение числа успехов (появлений события) носит название биномиального распределения .
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение.
Событие А
–
достали белый шар. Тогда вероятности
, .
По
формуле Бернулли требуемая вероятность
равна ![]() .
.
Пример. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение.
Вероятность
рождения девочки
,
тогда .
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Следовательно, искомая вероятность
![]() .
.
Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Решение.
Здесь
опыт заключается в проверке каждой из
30 деталей на качество. Событие А -
«появление нестандартной детали», его
вероятность ,
тогда .
Отсюда по формуле Бернулли находим
.
Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:

Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них .
Решение. Событие В – ровно n испытаний до k -го появления события А – есть произведение двух следующий событий:
D – в n -ом испытании А произошло;
С – в первых (n–1) -ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
Надо заметить, что использование биномиального закона зачастую связано с вычислительными трудностями. Поэтому с возрастанием значений n и m становится целесообразным применение приближенных формул (Пуассона, Муавра-Лапласа), которые будут рассмотрены в следующих разделах.
1.8. Наивероятнейшее число успехов
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид:
Так как , то эти границы отличаются на 1. Поэтому , являющееся целым числом, может принимать либо одно значение, когда целое число () , то есть когда (а отсюда и ) нецелое число, либо два значения, когда целое число.
Пример. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь . Поэтому имеем неравенства:
![]()
Следовательно, .
Пример. Данные длительной проверки качества выпускаемых стандартных деталей показали, что в среднем брак составляет 7,5%. Определить наиболее вероятное число вполне исправных деталей в партии из 39 штук.
Решение.
Обозначая
вероятность выпуска исправной детали
через ,
будем иметь ![]() и
и ![]() (получение
бракованной детали и получение исправной
детали - события противоположные). Так
как здесь n=
39,
то искомое число можно найти из неравенств:
(получение
бракованной детали и получение исправной
детали - события противоположные). Так
как здесь n=
39,
то искомое число можно найти из неравенств:
Отсюда наивероятнейшее число исправных деталей равно 36 или 37.
Неравенства для наивероятнейшего числа успехов позволяют решить и обратную задачу: по данному и известному значению р определить общее число n всех испытаний.
Пример. При каком числе выстрелов наивероятнейшее число попаданий равно 16, если вероятность попадания в отдельном выстреле составляет 0,7? Т А к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли). ., находим, вероятности выводится по ... 45 Сама теория достаточно сложна и подробно излагается лишь в специальных учебниках по корпоративным...
Менеджмент учебник санкт-петербург издательство «союз»
Учебник... по аппарату построения (форма); – по характеру моделируемых объектов содержание ). По ... вероятности во всех случаях, то учебники по теории вероятностей (а заодно и данная глава ... Теория вероятностей утверждает, что случайные события , ... вычислений . ...
Приказ № от 2014 г. Рабочая программа по математике класс: 5 (базовый уровень)
Рабочая программаА. Г. Математика. 6 кл. Учебники по содержанию и по стилю выстроены так, чтобы... Глава 6. 4 2 2 - Введение в вероятность . §53 Достоверные, невозможные и случайные события Вероятность наступления событий . Достоверные, невозможные и случайные события ...
Проект основной образовательной программы мкоу бутурлиновская сош №1 Бутурлиновского муниципального района Воронежской области на 2012-2017гг
Основная образовательная программа... Случайные события и вероятность . Понятие о случайном опыте и случайном событии . Частота случайного события . Статистический подход к понятию вероятности . Вероятности противоположных событий . Достоверные и невозможные события . Равновозможность событий ...
Будем полагать, что результатом реального опыта (эксперимента) может быть один или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом .
Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу).
Случайными событиями (событиями), будем называть подмножества пространства элементарных событий W .
Пример 1. Подбросим монету один раз. Монета может упасть цифрой вверх - элементарное событие w ц (или w 1), или гербом - элементарное событие w Г (или w 2). Соответствующее пространство элементарных событий W состоит из двух элементарных событий:
W = {w ц,w Г } или W = {w 1 ,w 2 }.
Пример 2. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w 1 , w 2 , w 3 , w 4 , w 5 , w 6 }, где w i - выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2 ,w 4 ,w 6 }, A W .
Пример 3. На отрезке наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий W = - множество действительных чисел на единичном отрезке.
В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом.
Пространством элементарных событий называют произвольное множество W , W ={w }. Элементы w этого множества W называют элементарными событиями.
Понятия элементарное событие, событие, пространство элементарных событий , являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство W .
Событие W называется достоверным событием.
Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда .
Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е. W = {w 1 , w 2 , w 3 , w 4 , w 5 , w 6 }, где w i - выпадение i очков, - достоверное событие.
Невозможным событием называется пустое множество .
Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда .
Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда .
Пример 5. Бросаем один раз игральную кость. Выпадение более шести очков - невозможное событие .
Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Обозначается , .
Пример 6. Бросаем один раз игральную кость. Событие A тогда событие - выпадение нечетного числа очков. Здесь W = {w 1 , w 2 , w 3 ,w 4 , w 5 ,w 6 }, где w i - выпадение i очков, A = {w 2 ,w 4 ,w 6 }, = .
Несовместными событиями называются события
A и B , для которых A B = .Пример 7. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, событие B - выпадение числа очков, меньшего двух. Событие A B состоит в выпадении четного числа очков, меньшего двух. Это невозможно, A = {w 2 ,w 4 ,w 6 }, B = {w 1 }, A B = , т.е. события A и B - несовместны.
Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.
Пример 8. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = {w 1 , w 2 , w 3 , w 4 , w 5 , w 6 }, где элементарное событие w i - выпадение i очков. Событие A - выпадение четного числа очков, A B B = {w 5 , w 6 }.
Событие A + B = {w 2 ,w 4 , w 5 , w 6 } состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A , либо событие B. Очевидно, что A + B W .
Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB .
Пример 9. Бросаем один раз игральную кость. В этом опыте пространство элементарных событий W = { w 1 , w 2 , w 3 ,w 4 , w 5 ,w 6 }, где элементарное событие w i - выпадение i очков. Событие A - выпадение четного числа очков, A = {w 2 ,w 4 ,w 6 }, событие B - выпадение числа очков, большего четырех, B = {w 5 , w 6 }.
Событие A B состоит в том, что выпало четное число очков, большее четырех, т.е. произошли оба события, и событие A и событие B, A B = {w 6 } A B W .
Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A , но не принадлежащих B. Обозначается A\B .
Пример 10. Бросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = {w 2 ,w 4 ,w 6 }, событие B - выпадение числа очков, большего четырех, B = {w 5 , w 6 }. Событие A\ B = {w 2 ,w 4 } состоит в том, что выпало четное число очков, не превышающее четырех, т.е. произошло событие A и не произошло событие B, A\B W .
Очевидно, что
A + A = A, AA = A, ![]() .
.
Нетрудно доказать равенства:
, (A+B )C= AC + BC .
Определения суммы и произведения событий переносятся на бесконечные последовательности событий:
![]() , событие, состоящее
из элементарных событий, каждое из которых
принадлежит хотя бы одному из;
, событие, состоящее
из элементарных событий, каждое из которых
принадлежит хотя бы одному из;
![]() , событие, состоящее
из элементарных событий, каждое из которых
принадлежит одновременно всем .
, событие, состоящее
из элементарных событий, каждое из которых
принадлежит одновременно всем .
Пусть W - произвольное пространство элементарных событий, а - такая совокупность случайных событий, для которой справедливо: W , AB, A+B и A\B, если A и B.
Числовая функция P, определенная на совокупности событий , называется вероятностью, если: (A ) 0 для любого A из ; (W ) = 1;
Тройку называют вероятностным пространством .
Классическое определение вероятности
Вероятностью события А Р(A) называется отношение числа благоприятствующих этому событию исходов m к общему числу всех единственно возможных и равновозможных элементарных исходов n, Р(A)=.
Задача1
Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.
Решение:
Для начала найдем вероятность того, что ни одному из студентов не достанется билет с простыми вопросами.
Эта вероятность равна ![]()
Первая дробь показывает вероятность того, что первому студенту достался билет со сложными вопросами (их 17 из 20)
Вторая дробь показывает вероятность того, что второму студенту достался билет со сложными вопросами (их осталось 16 из 19)
Третья дробь показывает вероятность того, что третьему студенту достался билет со сложными вопросами (их осталось 15 из 18)
И так далее до пятого студента. Вероятности перемножаются т.к. по условию требуется одновременное выполнение этих условий.
Чтобы получить вероятность того, что хотя бы одному из студентов достанется билет с простыми вопросами надо вычесть полученную выше вероятность из единицы.
Ответ: 0,6009.
Задача2
Из множества всех последовательностей длины 10, состоящих из цифр 0; 1; 2; 3, наудачу выбирается одна. Какова вероятность того, что выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности.
Решение
Вероятность события A – «Выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности», согласно классическому определению, равна P (A ) = , где n – полное число равновероятных исходов; m – число исходов, благоприятствующих событию A .
Число способов заполнить 10 позиций в последовательности цифрами 0; 1; 2; 3 составляет, с учетом возможности повторения цифр, n = 410 = 220 = 1048576.
Число способов разместить 5 нулей на 10 позициях в последовательности при условии, что нули обязательно находятся на первом и десятом месте в последовательности, равно числу способов разместить три нуля на восьми свободных позициях в последовательности и равно числу сочетаний из 8 элементов по 3: = = 56.
Оставшиеся 8 – 3 = 5 позиций в последовательности будут заполнены цифрами 1; 2; 3. Число способов осуществить это, с учетом возможности повторения, равно 35 = 243.
Т.о., число исходов, благоприятствующих событию A
, равно m
= ×35 = 56×243 = 13608.
Искомая вероятность события A
равна:
P
(A
) = = 0,013.
Ответ:
P(A) = = 0,013.
Задача 3.
Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь без брака.
Решение.
В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т. к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны, единственно возможны. Таким образом, Событие - появилась деталь без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно 97 . Итак, Тогда ![]()
Задача 4.
Код банковского сейфа состоит из 6 цифр. Найти вероятность того, что наудачу выбранный код содержит различные цифры? Решение.
Так как на каждом из шести мест в шестизначном шифре может стоять любая из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех различных шестизначных номеров по правилу произведения будет . Номера, в которых все цифры различны, - это размещения из 10 элементов (10 цифр) по 6. Поэтому число благоприятствующих исходов . Искомая вероятность равна

Задача 5.
Между шестью фирмами (А, Б, В, Г, Д, Е), занимающимися продажей компьютерной техники, проводится жеребьевка на предмет очередности предъявления своей продукции на выставке потенциальным потребителям. Какова вероятность того, что очередь будет выстроена по порядку, т. е. А, Б, В, Г, Д, Е?
Решение.
Исход испытания - случайное расположение фирм в очереди. Число всех возможных исходов равно числу всех перестановок из шести элементов (фирм), т.е.Число исходов, благоприятствующих событию : m=
1, если очередь выстроена по порядку. Тогда ![]()
Задача 6.
В компании 10 акционеров, из них трое имеют привилегированные акции. На собрание акционеров явилось 6 человек. Найти вероятность того, что среди явившихся акционеров:
а) все трое акционеров с привилегированными акциями отсутствуют;
б) двое присутствуют и один не явился.
Решение
а) испытанием является отбор 6 человек из 10 акционеров. Число всех исходов испытания равно числу сочетаний из 10 по 6, т. е.![]()
Пусть событие - среди шести человек нет ни одного с привилегированными акциями. Исход, благоприятствующий событию ,- отбор шести человек среди семи акционеров, не имеющих привилегированных акций. Число всех исходов, благоприятствующих событию А
, будет ![]()
Искомая вероятность ![]()
б) пусть событие - среди шести явившихся акционеров двое с привилегированными акциями, а остальные четыре – с общими акциями. Число всех исходов, Число способов выбора двух человек из необходимых трех ![]() Число способов выбора оставшихся четырех акционеров среди семи с общими акциями
Число способов выбора оставшихся четырех акционеров среди семи с общими акциями ![]() Тогда число всех способов отбора по правилу произведения
Тогда число всех способов отбора по правилу произведения
Искомая вероятность равна ![]()