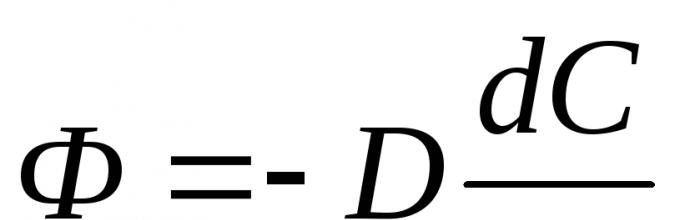Для описания пассивного транспорта – диффузии ионов в биофизике используется электродиффузионная теория, в соответствии с которой суммарный поток ионов через мембрану при пассивном транспорте определяется 2-мя факторами: неравномерностью их распределения (градиентом концентрации) и воздействием электрического поля (электрическим градиентом). Плотность потока ионов для разбавленных растворов определяется по уравнению Нернста-Планка:

где: Ф - поток вещества, u - подвижность иона, молекулы, R - универсальная газовая постоянная (8,314 Дж/моль*К), Т - температура по шкале К 0 , dC/dx - концентрационный градиент, С - концентрация в молях, Z - величина заряда иона, F - число Фарадея (96500 Кл/моль), dφ /dx - градиент потенциала.

Знаки минус перед градиентами показывают, что градиент концентрации вызывает перенос вещества от мест с большей концентрацией в места с меньшей; а градиент потенциала вызывает перенос положительных зарядов от мест с большим потенциалом к местам с меньшим.

Для описания диффузии незаряженных частиц используют уравнение Фика:

В этом виде уравнение Фика определяет поток незаряженных частиц через единичную площадь в случае, если не существует перегородки (мембраны), которая может затруднять перенос, где:

D D - коэффициент диффузии,- градиент концентрации

Для клеточной мембраны: dx = L - толщина мембраны, dC = С i - С e , где С i и С e -концентрация частиц внутри и снару­жи клетки. В уравнение Фика для клетки добавляется коэффици­ент К (коэффициент распределения), который определяет соотно­шение концентрации частиц между средой и мембраной и в ко­нечном итоге скорость переноса. Учитывая это, уравнение Фика для клеточной мембраны представляется в виде:

DK / L = Р - называют эффективным коэффициентом прони­цаемости, тогда Ф = - Р (С e - Сi)

6. Механизм активного транспорта ионов К+ и Na + через мембрану. Основные этапы работы K , Na - АТФ-азы. Энергозатраты противоградиентного переноса (формула).

Ионы Na и К определяют водно-электролитный обмен организма. В норме в живых клетках животных существует асимметрия концентраций этих ионов внутри (i) и снаружи (e) клетки. Концентрация К больше внутри клетки, концентрация Na больше снаружи. Клеточная мембрана одинаково проницаема для обоих ионов. Поэтому для поддержания асимметрии осуществляется противоградиентный перенос при помощи Na, К - АТФ-азы или Na-К насоса, за счёт энергии, освобождающейся при гидролизе АТФ.

АТФ +Н2О = АДФ + Ф н + ∆G, где Ф н – неорганический фосфат.

Основные этапы работы АТФ-азы:

1) Присоединение 3 ионов Na и фосфорилирование фермента внутри клетки.

2) Транслокация №1 –перенос центра связывания ионов Na наружу.

3) Отсоединение 3 ионов Na и замена их на 2 иона К.

4) Отщепление остатков фосфорной кислоты.

5) Транслокация №2 – перенос центра связывания ионов К внутрь клетки.

6) Отсоединение 2 ионов К и присоединение 3 ионов Na, затем фосфорилирование фермента.

Перенос 2 ионов К внутрь клетки и выброс 3 ионов Na наружу приводит в итоге к переносу одного дополнительного положительного заряда из цитоплазмы на поверхность мембраны. Поэтому внутриклеточное содержимое имеет знак (-), а внеклеточное (+). В целом, энергия, которая освобождается при гидролизе АТФ для осуществления активного транспорта Na + и К + , определяется формулой:

где первое слагаемое определяет энергию для противоградиентного переноса двух ионов К второе – энергию для противоградиентного переноса трёх ионов Na, третье – энергию на преодоление сил электрического поля, возникающего на мембране за счёт активного транспорта.

ДИФФУЗИИ УРАВНЕНИЕ - дифференциальное уравнение с частными производными 2-го порядка, описывающее процесс диффузии в случае, когда перенос вещества вызван лишь градиентом его концентрации (в отличие от термодиффузии и т. п.). Д. у. чаще всего записывают в виде

где и(x, t) - концентрация вещества в точке среды в момент времени t, D - коэф. , q - коэф. поглощения, a F - интенсивность источников вещества. Величины D, q и F обычно являются ф-циями x и t , а также могут зависеть от концентрации и(x, t) . B последнем случае ур-ние (1) становится нелинейным. В коэфф. диффузии D является тензорным полем.

Наиб. полно исследовано линейное Д. у., когда коэф. диффузии D и поглощения q - пост. величины. В этом случае ур-ние (1) является ур-нием параболич. типа, для к-poro в матем. разработаны разл. методы решения: метод разделения переменных, метод источников или функций Грина (см. также Винеровский функциональный интеграл) , метод интегр. преобразований и т. д. Для выделения единств. решения линейного ур-ния (1) необходимо также задать нач. и граничные условия (если диффундирующее вещество заполняет конечный объём V , огранич. боковой поверхностью S ). Обычно рассматривают след. линейные граничные условия для Д. у.: 1) на границе S поддерживается заданное распределение вещества u 0 (x, t): на S поддерживается заданная потока вещества, входящего в V через S:

где - внутр. нормаль к поверхности S; 3) S полупроницаема, и диффузия во внеш. среду с заданной концентрацией и 0 (x, t )через S происходит по линейному закону

Простейшее Д. у.

с нач. условием имеет решение вида

фундам. решение Д. у. (2).

Методы решения Д. у. с перем. коэф. диффузии менее развиты. В нек-рых частных случаях, напр. если D зависит только от концентрации и , можно аналитически найти точные решения Д. у. с перем. D .

Нелинейные матем. модели диффузии и (ур-ние и граничные условия) условно делят на след. классы: 1) от концентрации и зависят D или q (нелинейность 1-го рода); 2) нелинейность содержится в граничных условиях (нелинейность 2-го рода); 3) нелинейность возникает вследствие зависимости мощностей внутр. источников F от концентрации и (нелинейность 3-го рода, см. Диссипативные структуры ).

Одномерные нелинейные Д. у. можно решить разл. приближёнными аналитич. методами. Двухмерные и трёхмерные нелинейные Д. у. при сложной конфигурации границ области и сложных законах изменения характеристик среды, внеш. и внутр. источников вещества, перем. границ области, где происходит диффузия, поддаются решению только числ. методами с применением ЭВМ. С матем. точки зрения Д. у., являясь частным случаем дифференц. ур-ния, описывающего процесс установления равновесного распределения, совпадает с ур-нием теплопроводности и аналогично Навъе - Стокса уравнению для ламинарного потока несжимаемой жидкости и т. д.

Лит.: Владимиров В. С., Уравнения математической физики, 4 изд., M., 1981; Коздоба Л. A., Методы решения нелинейных задач теплопроводности, M., 1975; Pайченко А. И., Математическая теория диффузии в приложениях, К., 1981; Crank J., The mathematics of diffusion, 2 ed., Oxf., 1975. С. Я . Азаков .

В гл. ХIII, § 2, 6, мы исследовали интегральное уравнение (56) для теплопроводности и диффузии. Из метода его вывода ясно, что это уравнепие применимо и в более общем случае, рассматриваемом в этом пункте. Мы увидим, что в действительности оно имеет еще более общее значение. В самом деле, согласно принципу, изложенному в гл. ХIII, § 2, 3, функции, входящие в это уравнение, можно рассматривать как некоторые вероятности. Поэтому, если состояние некоторой физической системы определяется переменной зависящей от времени статистическим образом, т. е. совершающей некоторого рода броуновское движение, то это движение опять-таки будет описываться интегральным уравнением (51).

Если есть вероятность того, что система в момент времени находится между вероятность того, что система в течение времени переходит из начального положения, лежащего между конечное положение, лежащее между то удовлетворяет линейному интегральному уравнению:

ядро которого вообще говоря, несимметрично.

В случае обыкновенного броуновского движения, при отсутствии внешних сил, ядро симметрично относительно и имеет вид, определенный в гл. ХIII, §2, (56а). Там же указано решение "уравнения (8) в этом случае. Чтобы найти решение в общем случае, целесообразно преобразовать интегральное уравнение (8) в дифференциальное уравнепие следующим способом.

Введем сначала в уравнепие (8) вместо новую переменную представляющую собой смещение системы за время Тогда уравнение (8) примет вид:

где выражение очевидно, равно вероятности того, что система сместится за время из начального положения х на расстояние между и Примем теперь, что очень мало, и разложим левую часть (9) по степеням

с точностью до членов первого порядка, а правую часть по степеням у. Тогда мы получим

где величины имеют значение:

Из определения функции как вероятности непосредственно следует, что Предположим теперь, что существуют предельные значения:

Тогда из (10) получается дифференциальное уравнение для функции

где есть оператор

Это уравнение называется в статистическоё физике дифференциальным уравнением Фоккера-Планка Оно имеет самые разнообразные применения.

Если механическая система испытывает беспорядочные флуктуации иод действием внешних сил, с одной стороны, и вследствие теплового движения молекул - с другой, как это имеет место при обыкновенном броуновском движении, то функция согласно (11) и (12), есть средняя скорость приобретаемая частицами под действием внешних сил. Далее, в этом случае а все при тождественно равны нулю. Таким, образом, (13) переходит в обобщенное уравнение диффузии (6), где есть коэффициент диффузии. Согласно (11) и (12):

т. е. равно среднему квадрату смещения, деленному на соотношение, которое мы уже встречали в гл. XIII, § 2, (23) под названием формулы Эйнштейна.

Если внешние силы отсутствуют, т. е. если функция в (8) симметрична относительно то функция согласно (12), тождественно равна нулю, и (13) переходит в обыкновенное дифференциальное уравнение диффузии гл. XIII, § 1 (22). Поэтому всякая функция, определяемая интегральным уравнением (50) гл. § 2, должна одновременно удовлетворять уравнению (22) гл.

Если же внешние силы не равны нулю, то можно найти стационарное решение и уравнения Фоккера-Планка, соответствующее состоянию, устанавливающемуся через достаточно большой промежуток времени независимо от начального состояния. В этом случае и есть вероятность пребывания системы в промежутке между или относительное число тождественных систем, находящихся в этом интервале, если в начальный момент они были распределены

Явлением диффузии называется процесс установления внутри фаз равновесного распределения концентраций.

Результатом диффузии при постоянной температуре является выравнивание химических потенциалов. В однофазной системе при постоянной температуре и при отсутствии внешних сил диффузия выравнивает концентрацию компонента фазы во всей системе. Если на систему действуют внешние силы или поддерживается градиент температуры, то в результате диффузии устанавливаются градиенты концентраций отдельных компонентов (термодиффузия, электродиффузия и другие процессы).

Уравнение диффузии в одномерном случае

Уравнение диффузии в одномерном случае () в двухкомпонентной системе - это первый закон Фика:

где dm – масса первого компонента, которая переносится за время dt через элементарную площадку dS в направлении нормали x к рассматриваемой площадке в сторону убывания плотности первого компонента, – градиент плотности, D – коэффициент диффузии.

Если в однокомпонентной системе выделить группу молекул, выравнивание концентрации выделенных частиц по объёму сосуда называется самодиффузией. Самодиффузия тоже описывается уравнением диффузии (первым законом Фика), в котором коэффициент D- называется коэффициентом самодиффузии.

Уравнение диффузии в трехмерном случае

В случае трехмерной диффузии изменение концентрации с течением времени при постоянной температуре и отсутствии внешних сил описывается дифференциальным уравнением диффузии:

где D- коэффициент диффузии, t- время. Если D не зависит от концентрации, то уравнение диффузии будет иметь вид:

Уравнение (3) еще называют вторым законом Фика, где - дифференциальный оператор Лапласа.

В том случае, если перенос вещества вызван лишь градиентом его концентрации уравнение диффузии можно записать и в следующем виде:

где c(x, t) - концентрация вещества в точке среды в момент времени t, D – коэффициент диффузии, q - коэффициент поглощения, a F - интенсивность источников вещества. Величины D, q и F обычно являются функциями координат и времени, а также могут зависеть от концентрации с(x, t). B последнем случае, уравнение диффузии (4) становится нелинейным. В анизотропной среде коэффициент диффузии D является тензорным полем. В случае, когда величины D и q постоянны уравнение (4) является уравнением параболического типа. Для такого типа уравнений в математической физике разработаны методы решения. Допущение о постоянстве коэффициента диффузии справедливо в большинстве случаев реализуемых на практике. Уравнения диффузии не содержат ни каких сведений о механизмах этого процесса. Основная цель решения уравнения - найти распределение примеси c(x,t) после диффузии в течение определенного времени при различных условиях осуществления процесса.

Решение уравнения диффузии

Для выделения единственного решения для уравнения (4) необходимо задать начальные и граничные условия. Обычно, рассматривают следующие граничные условия:

1) на границе поверхности S поддерживается заданное распределение вещества

2)на границе поверхности S поддерживается заданная плотность потока вещества, входящего в V через границу S:

где n – внутренняя нормаль к поверхности S

3) S- полупроницаема, и диффузия во внешнюю среду с заданной концентрацией через поверхность S происходит по линейному закону:

В простейшем случае, когда диффузия происходит только вдоль одной прямой и c=c(x,t)уравнение (3) запишется в виде:

с начальным условием:

Тогда уравнение (5) имеет решение вида:

Текущая координата интегрирования.

Выражение (6) называется фундаментальным решением уравнения диффузии в случае (5).

Примеры решения задач

ПРИМЕР 1

Задание	Найти массу газа ( с молярной плотностью прошедшего вследствие диффузии через площадку за время , если градиент плотности в направлении, перпендикулярном площадке, равен . Температура газа T, средняя длинна свободного пробега молекулы .
Решение	Запишем первый закон Фика в терминах условий задачи: Знак минус означает, направление вектора плотности. Возьмем модуль от правой части выражения (1.1): Зная, что , где - средняя длина свободного пробега молекулы, - средняя скорость молекулы газа и она равна: . Соответственно преобразуем (1.2), найдем искомую массу газа:
Ответ	Искомая масса газа может быть найдена по формуле:

Процессов в твердых телах.

Определение диффузии. Первое и второе уравнения Фика.

Определим диффузию как процесс переноса вещества из одной части системы в другую, происходящий под действием градиента концентрации. Отметим, однако, что градиент концентрации – важная, но не единственная причина, вызывающая перенос вещества в системе.

При свободной диффузии не взаимодействующих между собой частиц (в отсутствии приложенных внешних сил) в однородном и изотропном твердом теле поток диффузионных частиц https://pandia.ru/text/80/099/images/image002_18.gif" width="53" height="25 src="> (для одномерного случая). Связь между ними определяется первым законом Фика:

где - коэффициент диффузии атомов. Из выражения (10.1) можем определить коэффициент диффузии как скорость, с которой система способна при заданных условиях сделать нулевой разность концентраций. Знак “минус” в выражении означает, что поток атомов направлен из области с большей концентрацией в область с меньшей концентрацией. Для трехмерной задачи первое уравнение Фика имеет вид:

где - оператор Набла, который записывается .

В случае независимости коэффициента диффузии от концентрации легирующих частиц, применение закона сохранения вещества при диффузии в форме уравнения непрерывности для потока частиц позволяет перейти ко второму уравнению Фика, устанавливающему связь между концентрацией диффундирующих частиц в различных точках тела и временем диффузии:

Для трехмерного случая:

https://pandia.ru/text/80/099/images/image010_8.gif" width="88" height="48">, (10.4)

где - оператор Лапласа, который записывается .

Второй закон Фика, как закон сохранения вещества, можно записать в форме уравнения непрерывности:

. (10.5)

Размерность плотности потока вещества зависит от размерности концентрации..gif" width="219" height="48">.

Одним из основных параметров диффузии является коэффициент диффузии, вводимый как коэффициент пропорциональности между потоком и градиентом концентрации вещества в уравнении (10.1). В зависимости от условий проведения диффузионного опыта, различают несколько типов коэффициента диффузии.

1. Для описания взаимной диффузии при контакте двух образцов неограниченно растворимых один в одном, пользуются понятием коэффициента взаимной диффузии https://pandia.ru/text/80/099/images/image017_4.gif" width="21 height=25" height="25">, равным коэффициенту взаимной диффузии, если собственные коэффициенты диффузии компонентов равны между собой, т. е..gif" width="17" height="19 src="> и ).

3. Кроме того, подвижность - того компонента сплава может быть охарактеризована порциальными коэффициентами диффузии , которые вводятся следующим образом:

. (10.6)

Порциальные коэффициенты можно определить как для собственной, так и для взаимной диффузии. Все введенные до сих пор коэффициенты являются коэффициентами гитеродиффузии (химической диффузии), т. е. такой диффузии, которая имеет место при наличии только градиента концентрации.

Диффузия в реальных кристаллах происходит вследствие четырех основных механизмов:

1. Для идеальных кристаллов процесс диффузии предполагает простой обмен местами между соседними атомами вещества. В этом случае необходимо затратить значительную энергию (порядка энергии связи между соседними атомами решетки).

2. Для примесей внедрения характерно перемещение атомов по междоузлиям из-за наличия в системе некоторой концентрации дефектов.

3. При вакансионном механизме диффузии один из соседних атомов занимает близлежащую вакансию. Вакансии могут образовываться вследствие того, что некоторые атомы, совершающие тепловые колебания около положения равновесия, могут иметь энергию, значительно превышающую среднюю энергию связи. Такие атомы уходят из узлов решетки в междуузельное пространство, образуя вакансию. Такая вакансия перемещается в кристалле путем последовательного заполнения ее другими атомами.

4. Возможна также диффузия по междоузлиям путем вытеснения, когда атом выталкивает одного из ближайших соседей в междоузлие, а сам занимает его место в решетке.

Таким образом, мы видим, что в твердых телах благодаря тепловому движению происходит непрерывное перемешивание частиц..gif" width="120" height="52">, (10.7)

где - энергия активации диффузии; - постоянная, равная по порядку величины периоду собственных колебаний атомов в узлах решетки https://pandia.ru/text/80/099/images/image029_2.gif" width="109" height="25 src=">, где - энергия активации при https://pandia.ru/text/80/099/images/image032_1.gif" width="15" height="20"> зависит от характера колебаний атомов.

В большинстве случаев коэффициент диффузии в твердых телах увеличивается с ростом температуры по закону, имеющему вид уравнения Аррениуса:

, (10.8)

где - предэкспоненциальный множитель (фактор), численно равный коэффициенту диффузии при бесконечно большой температуре.

Процессы взаимной диффузии в поликристаллических пленках металлов приводят к образованию интерметаллидов. При этом можно выделить следующие изменения их свойств:

1. Образуются металлические слои, структура которых имеет большое количество дефектов, через которые возможна диффузия примесей и газов.

2. Электронные характеристики пленок металлов из-за образования твердых растворов металлов и соединений изменяются.

3. Меняется толщина и состав переходного слоя.

4. Возможно развитие неоднородностей в слоях металлов и в переходном слое из-за неравномерности взаимной диффузии металлов через границу раздела.

Отмеченные выше процессы приводят к деградации электрических параметров и зависят от количества продиффундированного в структуру вещества. Поэтому особенно важно уметь находить зависимости распределения концентрации диффундирующих примесей в структурах от времени и температуры процесса диффузии. Это можно сделать, решив второе уравнение Фика или уравнение диффузии.

Уравнение диффузии представляет собой дифференциальное уравнение в частных производных и для его решения необходимо сформулировать начальные и граничные условия, которым должна удовлетворять концентрация и первоначальное распределение диффундирующего вещества. Эти условия определяют на основе анализа конкретной ситуации, в которой происходит процесс диффузии. Здесь важно отметить, что внутри твердого тела концентрация является непрерывной функцией координат и времени, а ее первая производная по времени и первая и вторая производные по координатам , и DIV_ADBLOCK165">

Начальное распределение концентрации может быть произвольным, но чаще всего эта функция постоянна либо равна нулю. Что касается граничных условий (условий на поверхности), то обычно в задачах диффузии задана либо концентрация на поверхности , либо поток https://pandia.ru/text/80/099/images/image042.gif" width="45" height="20"> переходы, глубина которых контролируется с точностью до долей микрометра.

Контрольные вопросы

1. Что такое диффузия?

2. Как записывается первое уравнение Фика?

3. Как записывается второе уравнение Фика?

4. Что такое коэффициент диффузии?

5. Какие различают типы коэффициентов диффузии?

6. Как записывается зависимость изменения коэффициента диффузии от температуры в твердом теле?

7. Как процессы взаимной диффузии и образование при этом интерметаллидов изменяют свойства пленок металлов?

8. Как можно задавать начальное распределение концентрации и граничные условия (условия на поверхности) при решении уравнения диффузии?