Архимед (287 г. до н. э. -- 212г. до н. э.) -- древнегреческий математик, физик и инженер из Сиракуз (остров Сицилия). Он сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений.
Архимедова спираль была открыта Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.
Архимедову спираль использовали в древности, как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга.
В III веке да нашей эры Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов, расположенных ниже. Позже на основе винта Архимеда создали шнек («улитку»). Его очень известная разновидность - винтовой ротор в мясорубке. Шнек используют в механизмах для перемешивания материалов различной консистенции.
Определение спирали Архимеда
Кривую можно рассматривать как траекторию точки, равномерно движущейся по лучу, исходящему из полюса, в то время как этот луч равномерно вращается вокруг полюса.
Представим себе циферблат часов с длинной стрелкой. Стрелка движется по окружности циферблата. А по стрелке в это время перемещается с постоянной скоростью маленький жучок. Траектория движения жучка представляет собой спираль Архимеда.
Построение спирали Архимеда
Чтобы понять, как получается спираль Архимеда, отметим на чертеже точку, которая является центром спирали Архимеда.
Построим из центра спирали окружность, радиус которой равен шагу спирали. Шаг спирали Архимеда равен расстоянию, которое проходит точка по поверхности круга за один его полный оборот.
Разделим окружность на несколько равных частей с помощью прямых линий. На первой линии откладываем одно деление, на второй-два деления, на третьей-три деления и т. д. Затем чертим соответствующее число дуг из центра окружности, проходящих через первое деление,2-ое и т. д.
Расстояния витков правой спирали, считая по лучу, равны,а расстояния соседних витков, равны.
Уравнение Архимедовой спирали имеет вид:
где - радиус-вектор,- угол вращения,- шаг спирали.
Полярный угол мы отсчитываем от полярной оси, считая его положительным против часовой стрелки.
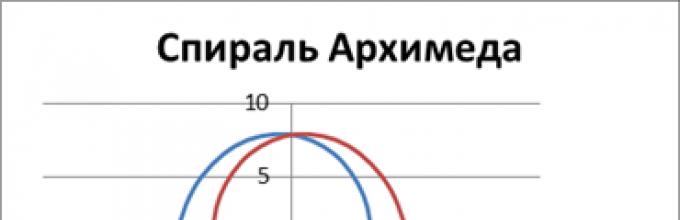
При вращении луча против часовой стрелки получается правая спираль (синяя линия) при вращении -- по часовой стрелке -- левая спираль (красная линия).
Полярный радиус-вектор мы будем брать как положительным, так и отрицательным; в первом случае его откладывают в направлении, определяемом углом, а во втором в противоположном направлении.

I.Вычислим площадь, описываемую полярным радиусом спирали при одном его обороте, если началу движения соответствует,




Если мы найдем площадь круга радиуса,то получим
Вообразим бесконечно длинную секундную стрелку, по которой, начиная от центра циферблата, неутомимо бежит маленький жучок с постоянной скоростью v см/с. Через минуту жучок будет на расстоянии 60v см от центра, через две - 120v и т.д. Вообще, через t секунд после начала пробега расстояние жучка от центра будет равно vt см. За это время стрелка повернется на угол, содержащий 6 t° (ведь за одну секунду она успевает повернуться на угол 360°:60 = 6°). Поэтому положение жучка на плоскости циферблата через любое число t секунд после начала движения находится так. Нужно отложить от начального положения стрелки в направлении ее вращения угол а, содержащий 6t°, и отмерить от центра вдоль нового положения стрелки расстояние r = vt см. Тут мы и настигнем жучка.
Очевидно, что соотношение между углом поворота a стрелки (в градусах) и пройденным расстоянием r (в сантиметрах) будет такое:
Иными словами, r прямо пропорционально a, причем коэффициент пропорциональности k = v/6.
Приладим к нашему бегуну маленькую, но неистощимую баночку с черной краской и допустим, что краска, вытекая через крошечное отверстие, оставляет на бумаге след от уносимого вместе со стрелкой жучка. Тогда на бумаге будет постепенно вырисовываться кривая, впервые изученная Архимедом (287 - 212 до н.э.). В его честь она называется спиралью Архимеда. Нужно только сказать, что у Архимеда не было речи ни о секундной стрелке (тогда и часов с пружиной не было: их изобрели только в XVII в.), ни о жучке. Мы ввели их здесь для наглядности.
Спираль Архимеда состоит из бесконечно многих витков. Она начинается в центре циферблата, и все более и более удаляется от него по мере того, как растет число оборотов. Вы, наверное, слышали, что с помощью циркуля и линейки невозможно разделить на три равные части наудачу взятый угол (в частных случаях, когда угол содержит, например, 180°, 135° или 90°, эта задача легко решается). А вот если пользоваться аккуратно начерченной архимедовой спиралью, то любой угол можно разделить на какое угодно число равных частей.
Разделим, например, угол АОВ на три равные части. Если считать, что стрелка повернулась как раз на этот угол, то жучок, будет находиться в точке N на стороне угла. Но когда угол поворота был втрое меньше, то и жучок был втрое ближе к центру О. Чтобы найти это его положение, разделим сначала отрезок ON на три равные части. Это можно сделать с помощью циркуля и линейки. Получим отрезок ON 1 , длина которого втрое меньше, чем ON. Чтобы вернуть жучка на спираль, нужно сделать засечку этой кривой радиусом ON 1 (снова циркуль!). Получим точку М. Угол АОМ и будет втрое меньше угла AON.
Самого Архимеда занимали, однако, другие, более трудные задачи, которые он сам поставил и решил: 1) найти площадь фигуры, ограниченной первым витком спирали (на рис. 11. она заштрихована); 2) получить способ построения касательной к спирали в какой-либо ее точке N.
Замечательно, что обе задачи представляют собой самые ранние примеры задач, относящихся к математическому анализу. Начиная с XVII в., площади фигур вычисляются математиками с Помощью интеграла, а касательные проводятся с помощью производных. Поэтому Архимеда можно назвать предшественником математического анализа.
Для первой из названных задач мы просто укажем результат, полученный Архимедом: площадь фигуры составляет точно 1/3 площади круга радиуса О А. Для второй задачи можно показать ход ее решения, несколько упростив при этом рассуждения самого Архимеда. Все дело в том, что скорость, с которой жучок описывает спираль, в каждой точке N направлена по касательной к спирали в этой точке. Если будем знать, как направлена эта скорость, то и касательную построим.
Но движение жучка в точке N складывается из двух различных движений (рис. 13.): одно - по направлению стрелки со скоростью v см/с, а другое - вращательное по окружности с центром в О и радиусом ОN. Чтобы представить последнее, допустим, что жучок замер на мгновенье в точке N. Тогда он будет уноситься вместе со стрелкой по окружности радиуса ON. Скорость последнего вращательного движения направлена по касательной к окружности. А какова ее величина? Если бы жучок мог описать полную окружность радиуса ON, то за 60 секунд он проделал бы путь, равный 2л ON [см]. Так как скорость при этом оставалась бы постоянной по величине, то для ее отыскания нужно разделить путь на время. Получим:
(2 л ON)/60 = (л ON)/30
Теперь, когда мы знаем обе составляющие скорости в точке N: одну по направлению ON, равную v см/с, и другую, к ней перпендикулярную, равную
(л ON)/30 см/с, остается сложить их по правилу параллелограмма. Диагональ представит скорость составного движения к вместе с тем определит направление касательной NT к спирали в данной точке.
Сакральная геометрия. Энергетические коды гармонии Прокопенко Иоланта
Последовательность Фибоначчи и спираль Архимеда
Плотная пища жен Фибоначчи
Только на пользу им шла, не иначе.
Весили жены, согласно молве,
Каждая – как предыдущие две.
Джеймс Линдон
Числовой ряд Фибоначчи – загадочная последовательность, воспетая в романах Дэна Брауна. В чем же уникальность и необычность этого ряда чисел? Почему несколько цифр, ставшие в ряд, привлекают так много внимания?
Числа Фибоначчи – это элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Числовой ряд Фибоначчи выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т. д.
Эта последовательность была известна в Древней Индии, ее широко использовали в стихосложении. Чуть позже ее использовал на Западе в своем труде «Liber Abaci» (1202) Леонардо Пизанский, более известный как Фибоначчи. Он рассматривал развитие идеальной популяции кроликов со следующей точки зрения:
– Изначально имеется пара кроликов (1 новая пара кроликов);
– В первом месяце пара производит на свет еще одну пару (1 новая пара кроликов);
– Во втором месяце каждая пара производит на свет еще по одной паре. Первая пара погибает (2 новые пары кроликов);
– В третьем месяце вторая пара и две новые пары кроликов порождают на свет три новые пары. Старая пара погибает (3 новые пары кроликов), и т.д.
Фибоначчи определил закономерным тот факт, кто каждая пара кроликов за всю жизнь порождает еще две пары, а затем погибает.
К чему мы об этом говорим? Казалось бы, ничего нового Фибоначчи не открыл, он напомнил миру о таком явлении, как золотое сечение (см. главу «Золотое сечение. Божественная пропорция»).
Однако числа Фибоначчи с легкостью можно найти в природе, в жизни, которая нас окружает. Будто все в мире построено одним великим архитектором. Числа Фибоначчи можно найти на стебле любого растения или в количестве лепестков.
Распределение листков тысячелистника по последовательности Фибоначчи
Последовательность Фибоначчи тесно связана с определением спирали Архимеда. Спираль Архимеда – спираль с равномерным увеличением шага и витка. Рассмотрим «золотой прямоугольник».

«Золотой прямоугольник»
Как видим, части в нем располагаются согласно вышеупомянутой последовательности. К тому же, если провести линии через углы этих квадратов в порядке возрастания, то мы получим не что иное, как уже известную спираль Архимеда.

Спираль Архимеда
В природе существует множество примеров того, как гармонично может воплощаться последовательность Фибоначчи. (Семена подсолнуха, сосновые шишки, ячейки ананаса, лепестки цветов.)
Молекулу ДНК человека составляют две переплетенные вертикально спирали длиной 34 и шириной 21. Недаром Гёте называл спираль «кривой жизни», ведь 21 и 34 – это цифры, следующие друг за другом в последовательности Фибоначчи.

Расположение семян подсолнуха

Паутина, построенная по принципу спирали Архимеда

Ракушка улитки, построенная по принципу спирали Архимеда

ДНК человека, построенная по принципу последовательности Фибоначчи
Числа Фибоначчи встречаются и в космосе, ведь Млечный путь и многие другие галактики построены по модели спирали Архимеда.

Млечный путь, одна из самых крупных спиралей Архимеда
Из книги Женщина-ягуар и мудрость дерева бабочек автора Эндрюс ЛиннГлава 8. Кальдера и священная спираль Мы ищем не отдыха – преображенья. Мы проходим друг в друга, как в двери. Мы сливаемся, скрещиваемся, уходим и возвращаемся, как волны, из сердцевины яблока, глаза мандалы, пустоты в цветке розы, безграничного круга с центром в
Из книги Тайны древних цивилизаций. Энциклопедия самых интригующих загадок прошлого автора Джеймс ПитерСПИРАЛЬ ГЛАСТОНБЕРИ ***В 1944 году ирландский бизнесмен Джеффри Расселл увидел необыкновенно яркий сон. Проснувшись, он немедленно перенес на бумагу образ, все еще стоявший у него перед глазами. Это был спиральный символ, состоящий из одной линии, закрученной в семь витков.
Из книги Проклятые книги автора Бержье ЖакДВОЙНАЯ СПИРАЛЬ Книжку профессора Джеймса Д. Уотсона «Двойная спираль» легко найти в любом книжном магазине. Его французский перевод был выпущен издательством «Robert Laffont». Существуют также несколько английских изданий в твёрдом переплёте и карманное издание в мягкой
Из книги Учебник по колдовству автора Каннингем СкоттГлава 9 Спираль перерождений Реинкарнация является самым спорным духовным явлением нашего времени. Реинкарнация - один из наиболее ценных уроков колдовства. Знание о том, что эта жизнь только одна из многих, и что, когда физическое тело умирает, мы не прекращаем своего
Из книги Тайны древних цивилизаций автора Джеймс ПитерСПИРАЛЬ ГЛАСТОНБЕРИ *** В 1944 году ирландский бизнесмен Джеффри Расселл увидел необыкновенно яркий сон. Проснувшись, он немедленно перенес на бумагу образ, все еще стоявший у него перед глазами. Это был спиральный символ, состоящий из одной линии, закрученной в семь витков.
Из книги В этой книге нет ни слова правды, но именно так все и происходит автора Фрисселл БобСпираль Вернемся же к квадрату, в который можно вписать человеческое тело, с вертикалью, делящей его пополам, и диагональю. Воспользуйтесь циркулем, чтобы повернуть диагональ, и завершите прямоугольник, продлив две оставшихся линии до их пересечения. Таким образом вы
Из книги Древняя Тайна Цветка Жизни. Том 1 автора Мельхиседек ДрунвалоСпираль Фибоначчи Математик средневековья Леонардо Фибоначчи открыл определенный порядок, или последовательность, в которой происходит рост растений. Вот эта последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Я уже упоминал о ней при обсуждении роста растений.
Из книги Четыре касты. Кто вы? автора Похабов Алексей8 Согласование полярностей бинарной последовательности и последовательности Фибоначчи Последовательность Фибоначчи и Спираль ФибоначчиДля того, чтобы понять, почему эти восемь спиралей вокруг Канона да Винчи не являются спиралями Золотого Сечения, и для понимания
Из книги Абсолютное исцеление. Системные и информационно-энергетические загадки нашего здоровья автора Гладков Сергей МихайловичГлава 4 Спираль качеств Если мы говорим о том, как стать Магом, то надо понимать следующее: эволюция человека происходит по чёткой последовательности. Нет прыжков из касты купцов в касту Магов. По ступеням придётся подниматься, наступая на каждую.Проблема в том, что нас
Из книги Математика для мистиков. Тайны сакральной геометрии автора Шессо РеннаИндивидуальная спираль исцеления Как бы нам ни хотелось найти «совершенную» систему питания, созданную кем-либо из великих, эти надежды, увы, несбыточны. Я много времени потратил, испытывая различные «системы», пока не понял: совершенная система – та, которую вы
Из книги Сакральная геометрия. Энергетические коды гармонии автора Прокопенко ИолантаГлава № 9 Фибоначчи, золотое сечение и пентакль Последовательность Фибоначчи - не просто случайная числовая схема, придуманная этим итальянским математиком. Она является плодом осмысления пространственных отношений, имеющих место в природе и впоследствии получившими
Из книги Большая книга тайных знаний. Нумерология. Графология. Хиромантия. Астрология. Гадания автора Шварц ТеодорСпираль. Виток материи жизни Спиральность – одна из характерных признаков всех организмов, как проявление самой сущности жизни. И. Гёте Амбивалентный, неоднозначный сакральный символ. Спираль одновременно воплощает в себе символику жизни и смерти, развития на
Из книги Свободный разум. Практики для тела, души и духа автора Кацудзо НишиСпираль Архимеда и закон октав Искусство – и я имею в виду подлинное, доброе искусство – зиждется, помимо всего прочего, на принципах баланса, динамики, местоположения и композиции. Эти элементы должны находиться в гармонии, взаимодействовать друг с другом, чтобы
Из книги автораПостроение спирали Архимеда Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.На первом луче путем проведения дуги радиусом
Из книги автораПоследовательность Фибоначчи С историей золотого сечения связано имя математика Леонардо из Пизы, известного под именем Фибоначчи (сын Боначчи). Он был самым знаменитым математиком Средневековья. В 1202 году вышел в свет его труд «Книга об абаке» (счетной доске), где были
Из книги автораМедитация на спираль Медитация со спиралью потребует времени, проводить ее надо в течение часа. Лучше для медитации выбрать утренние или дневные часы выходного дня. Создайте в комнате для медитирования полумрак, зажгите свечу. Сядьте прямо и постарайтесь отбросить все
Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).
Что такое спираль Архимеда?
Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны . В машиностроении спирали используются при проектировании пружин , косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.
Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons .
В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.
Уравнение спирали Архимеда в полярной системе координат записывается, как:
где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 \pi b . Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью . Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.
Задание параметризированной геометрии спирали Архимеда
Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.
Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:
\begin{align*} x_{component}=rcos(\theta) \\ y_{component}=rsin(\theta) \end{align*}
После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:
\begin{align*} x_{component}=(a+b\theta)cos(\theta) \\ y_{component}=(a+b\theta)sin(\theta) \end{align*}
В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final} , соответственно, и количество витков n . Показатель роста спирали b находится, как:
b=\frac{a_{final}-a_{initial}}{2 \pi n}
Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f , соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 \pi n . Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.
Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):
\begin{align*} X_{fun}=(a+bs)cos(s) \\ Y_{fun}=(a+bs)sin(s) \\ \end{align*}

Выражение для X-компоненты уравнения спирали Архимеда, заданное
аналитической функцией.
Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0 , до его конечного значения, theta_f=2 \pi n .

Настройки для Parametric Curve (Параметрической кривой).
Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.
До этого момента параметрами нашей кривой были начальный (a_{initial} ) и конечный (a_{final} ) радиусы и количество витков n . Теперь мы хотим добавить ещё один – толщину спирали.
Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 \pi b . Что эквивалентно \frac{a_{final}-a_{initial}}{n} . Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap .

Расстояние между витками определяется толщиной спирали и величиной зазора.
\begin{align*} distance=\frac{a_{initial}-a_{final}}{n} \\ gap=distance-thick \end{align*}
После этого выражаем показатель роста спирали через толщину:
\begin{align*} distance=2\pi b \\ b=\frac{gap+thick}{2\pi} \end{align*}
Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:
\begin{align*} \theta_{final}=2 \pi n \\ a_{final}=\text{total distance}+a_{initial} \\ a_{final}=2 \pi bn+a_{initial} \\ n=\frac{a_{final}-a_{initial}}{2 \pi b} \\ \theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\ \theta_{final}=\frac{a_{final}-a_{initial}}{b} \end{align*}
Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0 .
Дублирование кривой спирали дважды со смещением на -\frac{thick}{2} и +\frac{thick}{2} по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения \pm\frac{thick}{2} на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:
n_x=-\frac{dy}{ds} \quad \text{and} \quad n_y=\frac{dx}{ds}
где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:
\sqrt{(dx/ds)^2+(dy/ds)^2 }
Обновленные параметрические уравнения спирали Архимеда со смещением:
\begin{align*} x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\ y_{component}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \end{align*}
Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:
\begin{align*} N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\ N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }} \end{align*}
где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_{fun} и Y_{fun} в первом примере. Внутри функции используется оператор производной, d(f(x),x) , как показано на скриншоте ниже.

Примеры оператора производной, который используется в
аналитической функции
Функции X_{fun} , Y_{fun} , N_x , и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:
\begin{align*} x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\ y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2} \end{align*}
Так и с другой:
\begin{align*} x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\ y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2} \end{align*}

Выражения для второй смещённой параметрической кривой.
Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_{fun} , Y_{fun} , N_x , и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:
\begin{align*} X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\ Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2} \end{align*}
Уравнения кривой на конце:
\begin{align*} X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\ Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2} \end{align*}
В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid , создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.
Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics
В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.
Дополнительные ресурсы по проектированию и расчёту спиралей
- Для улучшения навыков моделирования спиралей, ознакомьтесь со следующими учебными моделями:
- Познакомьтесь с опытом одного из наших пользователей:
Инструкция
Отметьте на чертеже точку, которая является центром спирали Архимеда . Обозначьте центр буквой O.

Полярные координаты ρ=ρ(φ) следует вводить, используя фокус, как центр. Тогда можно положить ρ=r2 и после незначительных преобразований получите для правых участков эллипса и параболы полярные уравнения (см. рис. 3). При этом а – большая полуось эллипса (мнимая для гиперболы), с – абсцисса фокуса, про параметр b – на рисунке.

Приведенная на формулах рисунка 2 величина ε называется эксцентриситетом. Из формул рисунка 3 следует, что все прочие величины с ней как-либо связаны. И действительно, поскольку ε связана со всеми главными кривыми второго порядка, то на ее основе и можно принимать основные решения. А именно, если ε1 – гипербола. ε=1 – . Это имеет и более глубокий смысл. В куда как крайне сложном курсе «Уравнения математической » дифференциальных уравнений с частными производными производится на этой же основе.
Источники:
- Psi coma. Автор Как Просто. Как привести к каноническому виду уравнение.
- Psi coma. Автор Как Просто. Как привести уравнение к каноническому виду.
Жизнь современной представительницы прекрасного пола не ограничивается лишь семьей и детьми. Большую часть времени занимает работа. Чтобы успеть справиться со всеми своими многочисленными обязанностями, женщине нужно строго планировать свое время, свои нагрузки и, в том числе, количество детей и время их появления. Решить эти задачи помогают современные средства контрацепции.

Вы сможете спокойно кормить грудью, не думая о составе таблеток, которые с молоком могут попасть в его организм. В сравнении со презервативом, который относится к так называемому «барьерному методу», спираль неожиданно не порвется, сделав вас обладательницей еще одного малыша.
Когда же можно после родов? Чаще - через шесть-восемь недель после рождения ребенка, когда врач убедится, что ваш организм в необходимой степени восстановился и каких-либо противопоказаний нет. После сечения спираль ставится только через 6 месяцев.
Как действует спираль
Действие внутриматочной спирали основано на том, что она не позволяет яйцеклетке закрепиться в . Спирали бывают разные по форме - кольцевидные, т-образные и т.д. Их форма должна препятствовать выпадению этого устройства из полости матки. Необходимый противозачаточный эффект спирали достигается за счет ионов меди или другого вещества, которое находится на ее стержне.
На некоторых спиралях вместо меди используется серебро, прополис или золото. Это более дорогие средства защиты, но у них есть дополнительный противовоспалительный эффект. Существуют и гормоносодержащие спирали. Они предотвращают обильные болезненные менструации, которые могут быть после установки этого устройства.
Гормоносодержащие спирали придется менять через 1 год, когда в них истощается запас прогестерона, а спирали с медью - через 2-3 года.
Через несколько лет спираль заменяют на новую. Устанавливается она в последние дни менструации. В первый месяц после установки желательно ограничивать физические нагрузки.
Решать, ставить спираль после родов или нет, может только врач-гинеколог, причем очень опытный. Доверяться непрофессиональному врачу нельзя.
Продолжительность действия спирали указана на упаковке, она зависит от используемого активного вещества на стержне и иногда достигает 8 лет.
При отсутствии должного опыта у врача в лучшем случае вы столкнетесь с болями после , выделениями, в худшем - с выпадением этого устройства, развитием воспалительных явлений или даже опухолями.
В каждом конкретном случае вопрос об установке спирали после родов решается индивидуально с учетом пожеланий женщины и заключения врача о целесообразности использования этого средства контрацепции. В любой момент устройство можно извлечь, чтобы сделать возможным рождение еще одного желанного ребенка.