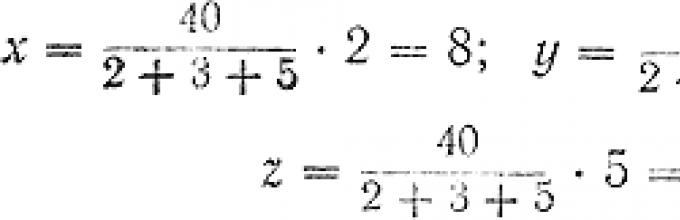§ 138. Деление числа на части прямо пропорционально данным числам.
Задача. В саду на двух участках посажено 224 штуки рассады клубники. Определить, сколько штук рассады посажено на каждом участке, если площадь первого участка 8 кв. м, а площадь второго 24 кв. м. (На каждом квадратном метре земли сажают рассаду в среднем поровну.)
Будем решать эту задачу так. Сначала определим площадь двух участков вместе:
8 + 24 = 32 (кв. м).
Итак, площадь двух участков вместе 32 кв. м. Определим теперь, сколько штук рассады приходится на 1 кв. м:
224: 32 = 7 (штук).
Зная сколько рассады приходится на 1 кв. м, мы легко вычислим число штук рассады на 8 кв. м и на 24 кв.. м, т. е. ответим на вопрос задачи:
7 8 = 56 (штук);
7 24 = 168 (штук).
Подумаем теперь, какие величины входят в нашу задачу и как они связаны между собой. В условие задачи входят две величины: 1) количество штук рассады, 2) площадь участка. Эти две величины прямо пропорциональны одна другой, потому что, чем больше площадь участка, тем больше на нём можно посадить рассады. Расположим числа, с которыми мы имели дело в задаче, так, чтобы их удобно было сравнивать:
8 кв. м - 56 штук
24 кв. м - 168 штук
Из этой таблички видно, что второй участок втрое больше первого и рассады на нём в три раза больше, чем на первом.
Итак, в этой задаче мы разделили число штук рассады пропорционально площадям двух участков. Это и есть одна из возможных задач на пропорциональное деление. Как же решаются такие задачи? В задаче требовалось число 224 разделить на две части, пропорциональные числам 8 и 24, т. е. разделить это число на такие две части, которые относились бы между собой так же, как 8: 24. Обозначим величину первой части буквой х , а второй части - у и напишем отношение этих частей:
Для нахождения этих частей были выполнены следующие действия. Число 224 разделили на сумму чисел 8 и 24 и затем найденное частное последовательно умножили сначала на 8, а потом на 24, т. е.
Словами эти равенства можно высказать так: чтобы разделить некоторое число на части пропорционально данным числам, надо разделить его на сумму этих чисел и полученное частное последовательно умножить на каждое из этих чисел.
Рассмотрим другую задачу: «За три куска мыла одного и того же сорта заплатили 40 руб, Сколько заплатили за каждый из них, если первый кусок весил 2 кг, второй 3 кг и третий 5 кг?»
В этой задаче требуется разделить 40 руб. на 3 части пропорционально весу отдельных кусков мыла. Обозначим стоимость первого куска буквой х , второго куска - у и третьего - z .
Воспользуемся правилом, выведенным при решении первой задачи. Согласно этому правилу для нахождения искомых чисел необходимо число, подлежащее делению, разделить на сумму данных чисел и полученное частное умножить последовательно на каждое из них. Следовательно:

Таким образом, первый кусок мыла стоит 8 руб., второй 12 руб. и третий 20 руб. Найденные числа рублей х, у, z находятся между собой в таких же отношениях, как и данные в задаче числа весовых единиц, т. е.
х: у: z = 8: 12: 20 = 2: 3: 5.
Рассмотрим теперь задачу с отвлечёнными числами. Разделить число 180 на три части пропорционально числам 3; 5; 7. Иными словами: в этой задаче требуется разложить число 180 на такие три слагаемых, чтобы первое относилось ко второму, как 3 к 5, второе относилось к третьему, как 5 к 7 и, наконец, первое к третьему, как 3 к 7. Сокращённо это можно написать так:
х: у: z = 3: 5: 7,
где х, у, z обозначают соответственно первое, второе и третье число.
Применяя указанное выше правило, можем написать:

Полученные три числа удовлетворяют условию задачи: они в сумме составляют 180, т. е.
36 + 60 + 84 = 180 и 3: 5: 7 = 36: 60: 84.
Мы решили три задачи на пропорциональное деление. Покажем теперь другие способы решения таких задач.
Задача 1. Определить квартирную плату за каждую из двух комнат (8 кв. м и 24 кв. м), если за обе вместе нужно заплатить 64 руб.
Обозначим плату за 1 кв. м буквой х ; тогда за первую комнату нужно будет заплатить 8x , а за вторую - 24x . Значит, за обе комнаты вместе надо заплатить 8х + 24х , что составляет 64 руб. Следовательно, можно записать равенство:
8х + 24х = 64.
32x = 64;
х = 64: 32 = 2 (руб.).
2 8 = 16 (руб.);
2 24 = 48 (руб.).
Задача 2. Найти стоимость каждого из трёх пакетов муки, если все три пакета стоят 40 руб., а вес первого 2 кг, второго 3 кг и третьего 5 кг.
Обозначим цену одного килограмма буквой х , тогда:
2 кг будут стоить 2х;
3 кг » » 3х ;
5 кг » » 5х ;
а вся мука будет стоить:
2х + 3х + 5х = 40.
10х = 40; х = 40: 10 = 4 (руб.).
После этого легко определить стоимость каждого пакета;
2х = 2 4 = 8 (руб.);
3х = 3 4 = 12 (руб.);
5х = 5 4 = 20 (руб.).
Задача 3. Разделить число 1 800 на три слагаемых пропорционально числам: 3, 5 и 7.
Рассуждаем так: в первом слагаемом 3 части, во втором 5 и в третьем 7.
Обозначая величину одной части буквой х , можно написать:
3х + 5х + 7х =1 800.
15х = 1 800; х = 1 800: 15 = 120.
Следовательно:
3х = 3 120 = 360;
5х = 5 120 = 600;
7х = 7 120=840.
Решим теперь задачу, в которой "некоторое число придётся разделить на четыре части пропорционально дробным числам.
Задача. Разделить 968 на четыре части пропорционально числам: 2 / 3 , 3 / 4 , 2 / 5 и 3 / 8 .Это значит, что надо найти четыре таких числа (х, у, z, t ), отношения которых были бы равны соответствующим отношениям данных чисел, т. е.

а сумма x + y + z + t = 968.
Заменим отношения дробных чисел отношениями целых чисел, для чего приведём эти дроби к общему знаменателю:

Отбрасывая общий знаменатель 40, получим: 60: 30: 16: 15. Вычислим последовательно каждое из искомых чисел:

§ 139. Деление числа на части обратно пропорционально данным числам.
Теперь перейдём к решению задач, в которых придётся некоторое число делить обратно пропорционально данным числам.
Задача. В двух полевых бригадах 70 колхозников. Каждой бригаде поручено обработать одинаковые участки. Сколько колхозников в каждой бригаде, если первая бригада выполнила работу в 6 дней, а вторая - в 8 дней? (Предполагается, что все колхозники работают с одинаковой производительностью труда.)
Очевидно, мы не имеем права делить число колхозников на две части пропорционально времени, которое каждая бригада употребила на работу, так как та бригада, которая быстрее окончила свою работу, была, по-видимому, более многочисленная, чем другая. Поэтому решать эту задачу так же, как мы решали предыдущие задачи, нельзя.
Будем рассуждать следующим образом. Первая бригада колхозников окончила свою работу в 6 дней; значит, в один день она выполняла 1 / 6 часть всей работы; вторая бригада окончила такую же работу в 8 дней, значит в один день она выполняла 1 / 8 всей работы.
Сравним теперь работу, которую выполняет в день первая бригаду с работой, выполняемой в день второй бригадой. Эти работы выражаются дробями 1 / 6 и 1 / 8 . Первая дробь больше второй. Значит, первая бригада в один день может делать больше, чем вторая. А так как все колхозники работают с одинаковой производительностью труда, то, значит, в первой бригаде больше колхозников, чем во второй. Таким образом, число колхозников в каждой бригаде пропорционально той работе, которую каждая бригада может выполнить. Значит, данное в задаче число 70 мы должны разделить на две части пропорционально числам: 1 / 6 и 1 / 8 . С задачами такого типа мы уже знакомы. Приведя дроби 1 / 6 и 1 / 8 к общему знаменателю, мы найдём числа, пропорционально которым следует разделить число 70:

т. е. число 70 нужно разделить на две части пропорционально числам 4 и 3. Обозначим число колхозников первой бригады буквой х , а второй - буквой у и вычислим:
Итак, в первой бригаде было 40 человек, а во второй 30. Рассмотрим теперь метод решения этой задачи. В условие задачи входят три числа: 70 (человек), 6 (дней) и 8 (дней). В процессе решения мы ввели еще два числа: 1 / 6 и 1 / 8 , и пропорционально этим дробям разделили число 70 на две части. Очевидно, что число 6 и число 1 / 6 взаимно обратны. Так же взаимно сбратны числа 8 и 1 / 8 .
Для решения задачи требуется разделить 70 рабочих на две неравные бригады, исходя из количества времени (дней), затраченного ими на работу. Это время выражается числами 6 (дней) и 8 (дней). Вместо этих двух чисел мы берём обратные им числа 1 / 6 и 1 / 8 и пропорционально им делим число 70.
Такая замена сделана нами потому, что число работников не прямо, а обратно пропорционально времени, затраченному на работу. О такой задаче принято говорить, что в ней число 70 разделено на две части обратно пропорционально числам 6 и 8, т. е. в ней первая часть относится ко второй не как 6 к 8, а как 8 к 6.
Итак, чтобы разделить число на части обратно пропорционально данным числам, нужно это число разделить прямо пропорционально обратным числам.
Задача. Разделить 65 на три части обратно пропорционально числам: 2, 3, 4.
Мы теперь знаем, что разделить число на части обратно пропорционально нескольким числам - это значит разделить его на столько же частей прямо пропорционально обратным числам.
Напишем числа, обратные данным в задаче:
данные числа 2, 3, 4;
обратные числа 1 / 2 , 1 / 3 , 1 / 4 .
Пропорционально этим последним и нужно разделить число 65. Приведём дроби к общему знаменателю:
а потом освободимся от него:
Значит, число 65 нужно разделить на три части пропорционально числам 6: 4: 3.
Обозначим первую часть буквой х , вторую часть буквой у , третью часть буквой z . Тогда
{module Адаптивный блок Адсенс в начале статьи}
ЗАДАЧИ НА ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ
4 КЛАСС
Задачи на пропорциональное деление получили свое название по способу их решения. Чтобы дать ответ на вопрос задачи необходимо составить некоторую пропорцию и рассчитать как соотносятся между собой искомые величины.
Рассмотрим решение задачи на пропорциональное деление на примере:
Задача: Двое рабочих заработали 9000 рублей. Один работал 2 недели, а другой 8 недель. Сколько денег заработал каждый?
Решение: Исходя из условия задачи, можно найти как оплачивается одна неделя такой работы:
9000 ÷ (8 + 2) = 900 рублей за неделю.
900 · 2 = 1800 рублей - один рабочий;
900 · 8 = 7200 рублей - другой рабочий.
Ответ: 1800 и 7200.
Примеры задач на пропорциональное деление:
1) Двое рабочих получили 8000 рублей. Как они разделят свой заработок, если один работал 6 недель, а другой 4 недели?
2) 25 м проволоки весят 700 г. Взяли два мотка проволоки. В одном мотке 30 м проволоки, а в другом на 15 м больше. Сколько весит каждый моток?
3) Для приготовления торфоперегнойных горшков берут на 7 частей земли 2 части торфа. Сколько нужно взять земли на 200 кг торфа?
4) Две школы выписали на 960 рублей клубничной рассады. Одна школа взяла 3 ящика, а другая 5 ящиков. Сколько должна заплатить каждая школа за рассаду клубники?
5) Два грузовика перевезли 77 т груза, сделав одинаковое число рейсов. Сколько тонн груза перевёз каждый грузовик, если один грузовик перевозил за рейс 3 т, а другой - 4 т?
6) Двое рабочих выписали из питомника 26 яблонь. Как они должны разделить яблони, если один дал на покупку 500 рублей, а другой 800 рублей?
7) Сколько граммов резинового клея получится из 50 г каучука, если для приготовления клея берут на одну часть каучука 9 частей очищенного бензина?
8) Двое рабочих заработали 8400 рублей. Первый работал 5 недель, а второй 7 недель. Сколько денег заработал каждый рабочий?
9) Две бригады работали одинаковое время и заработали вместе 810 рублей. Как они должны разделить этот заработок, если в одной бригаде было 4 человека, а в другой 5?
10) Клуб купил одинаковое число лыж и коньков. Пара коньков стоит 6 долларов, а пара лыж 9 долларов. Сколько стоят отдельно коньки и лыжи, если за всю покупку заплатили 900 долларов?
11) Для приготовления жидкого столярного клея берут 15 частей плиточного клея и 17 частей воды. Сколько нужно взять плиточного клея для изготовления 640 г жидкого столярного клея?
12) На 118 рублей купили одинаковое число пальто для мальчиков и девочек. Сколько куплено тех и других, если каждое пальто для мальчиков стоило 31 марку, а для девочек 28 марок?
13) Колхоз привёз одинаковое количество ящиков яблок и груш. Каждый ящик груш весил 50 кг, а ящик яблок 40 кг. Все фрукты вместе весили 810 кг. Сколько килограммов тех и других фруктов отдельно привезли?
14) В двух кусках 24 м сукна. Один кусок стоит 240 долларов, а другой 480 долларов. Сколько метров сукна в каждом куске?
15) "Москвич" на 100 км пути расходует 9 л бензина, "Волга" - 13 л. Обеим машинам отпущено 66 л бензина на 300 км пути. Сколько литров бензина отпущено каждой машине?
{module Адаптивный блок Адсенс в конце статьи}
Пропорция – равенство двух отношений: a/b = c/d (a, d – крайние члены пропорции; b, c – средние члены пропорции).
Основное свойство пропорции: ad = bc.
Две взаимно зависимых величины называютсяпропорциональными, если отношение их величин сохраняется неизменным. Это постоянное отношение пропорциональных величин называется коэффициентом пропорциональности. Например, в пропорции 0,04/4 = 0,12/12 коэффициент пропорциональности равен k = 0,01.
Если две величины связаны между собой так, что увеличение (уменьшение) одной (во столько же раз) увеличивает (уменьшает) пропорционально и другую величину, то такие величины прямо пропорциональны. Примерами прямой пропорциональности являются зависимость пройденного пути от времени (при постоянной скорости), периметра квадрата от длинны его стороны. Если зависимость величин прямо пропорциональна, то их значения составляют пропорцию х 1 /х 2 = у 1 /у 2 .
Если две величины связаны между собой так, что увеличение (уменьшение) одной (во столько же раз) уменьшает (увеличивает) пропорционально и другую величину, то такие величины обратно пропорциональны. Пример обратной пропорциональности: зависимость скорости от времени (при постоянном значении пройденного пути), производительности труда от времени затраченного на выполнение определенной работы (при одинаковом объеме работы). Если зависимость величин обратно пропорциональна, то их значения составляют пропорцию х 1 /х 2 = у 2 /у 1 .
Решая задачи на пропорциональную зависимость, важно разбить решение на такие этапы :
1. Условие задачи записать в виде схемы.
2. Определить тип зависимости между величинами.
3. Прямо пропорциональная зависимость обозначается одинаково направленными стрелками. Обратно пропорциональная зависимость – стрелками противоположно направленными.
4. Обозначить неизвестное через х, записать пропорцию и найти неизвестный член.
Рассмотрим решение нескольких задач на пропорциональную зависимость.
Задача 1.
За некоторое время велосипедист проехал 5 км со скоростью 10 км/ч. Какое расстояние он проедет за то же время, увеличив свою скорость в полтора раза?
Решение.
При постоянном значении времени пройденный путь и скорость величины прямо пропорциональные. Поэтому с увеличением скорости в полтора раза, значение пути тоже увеличится в столько же раз.
Значит, он проедет 5 · 1,5 = 7,5 (км).
Ответ: 7,5 км.
Задача 2.
На некотором участке газопровода трубы длинной 4 м заменили на трубы длинной 5 м. Сколько нужно новых труб для замены 100 старых?
Решение.
Так как увеличение длинны труб приведет к уменьшению их количества на одном и том же участке газопровода, то зависимость обратно пропорциональная. Составим схему по условию.
Запишем пропорцию: 4/5 = х/100.
Откуда, х = (4 · 100)/5 = 80 (труб).
Ответ: 80 труб.
Как видим, если в условии задачи рассматриваются две величины, то решение достаточно простое, главное правильно определить вид зависимости. Но как быть, если рассматривается зависимость между тремя величинами?
Задача 3.
За 5 дней 3 маляра окрашивают 60 окон. За сколько дней 2 маляра покрасят 48 окон?

Решение.
Примем количество рабочих за постоянную величину
(то есть работу выполняют постоянно 3 маляра) и рассмотрим зависимость между двумя величинами. Так как для покраски меньшего числа окон потребуется меньше дней при одном и том же количестве рабочих, то зависимость прямая.
Запишем пропорцию: 5/х = 60/48.
Откуда, х = (5 · 48)/60 = 4 (дня) – за столько дней покрасят 48 окон 3 маляра.
Для того, чтобы найти за сколько дней покрасят эти же 48 окон 2 маляра, составим таблицу, учитывая что постоянной величиной есть количество окон
. Так как для меньшего числа рабочих потребуется больше дней для выполнения одного и того же задания, то зависимость обратная.
Пропорция будет такой: 4/х = 2/3.
Откуда, х = (4 · 3)/2 = 6 (дней) – за столько дней покрасят 48 окон 2 маляра.
Ответ: 6 дней.
Потребность разделить величину или число в данном отношении часто возникает в практической жизни человека, например, во время приготовления блюд, разделения прибыли между партнерами по бизнесу и т.п. Поэтому важно владеть навыками решения задач на пропорциональное деление. Рассмотрим несколько примеров.
Задача 4.
Три компаньона вложили в организацию предприятия соответственно 280, 320 и 360 долларов. Прибыль, которую они получили, составила 2400 долларов. Сколько денег из прибыли получить каждый компаньон, если прибыль распределяется пропорционально вкладу каждого?
Решение.
Обозначим части прибыли, которые они должны получить, соответственно:
а: в: с = 280: 320: 360.
Упростим отношение:
а: в: с = 280: 320: 360 = 28: 32: 36 = 7: 8: 9.
Так как величины пропорциональны, то пусть х – коэффициент пропорциональности (одна часть прибыли). Тогда, а = 7х, в = 8х, с = 9х. Сумма частей должна равняться прибыли, тогда уравнение будет иметь вид:
7х + 8х + 9х = 2400.
Откуда х = 100 (дол). Следовательно, первый компаньон должен получить из прибыли:
7 · 100 = 700 (дол), второй 8 · 100 = 800 (дол), а третий 9 · 100 = 900 (дол).
Ответ: 700, 800, 900.
Задача 5.
Периметр треугольника АВС равен 32,5 см. Найти стороны треугольника, если АВ относится к ВС как 3: 4, а ВС относится к АС как 2: 3.
Решение.
Трудность заключается в том, что дано отношение не трех сторон, а первой ко второй и второй к третьей. Рассмотрим эти отношения:
АВ: ВС = 3: 4
ВС: АС = 2: 3.
Уравняем количество частей стороны ВС в первом и втором равенствах. Для этого второе отношение умножим на 2. Получим,
АВ: ВС = 3: 4
ВС: АС = 4: 6.
Теперь можем записать отношение трех сторон АВ: ВС: АС = 3: 4: 6. Тогда АВ = 3х, ВС = 4х, АС = 6х, где х – коэффициент пропорциональности.
Решая уравнение 3х + 4х + 6х = 32,5, получаем, что х = 2,5 (см).
Следовательно, стороны треугольника: АВ = 3 · 2,5 = 7,5 (см); ВС = 4 · 2,5 = 10 (см); АС = 6 · 2,5 = 15 (см).
Ответ: 7,5; 10; 15.
Задачи на пропорциональную зависимость развивают логическое мышление, учат анализировать и находить связи между величинами, а задачи на пропорциональное деление имеют широкое практическое применение, поэтому умение решать и те и другие просто необходимо.
Остались вопросы? Не знаете, как решать задачи на пропорциональную зависимость?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Характерные особенности такого вида задач:
1) В начальных классах решаются задачи на пропорциональное деление только с прямо пропорциональной зависимостью величин.
2) В начальных классах задачи на пропорциональное деление решаются только способом нахождения значения постоянной величины.
Подготовка:
1) Работа над величинами.
2) Связь между величинами.
3) Наблюдение за зависимостью между величинами.
4) Хорошее овладение способами решения задач на нахождение четвёртого пропорционального.
Ознакомление: первые задачи на пропорциональное деление иллюстрируются или инсценируются. Переход к ознакомлению можно осуществлять от задач на нахождение четвёртого пропорционального.
| Вид задачи | На пропорциональное деление |
| Условие | В магазин привезли 6 ящиков картофеля и 4 таких же ящика свёклы. Всего в магазин привезли 120 кг овощей. Сколько килограммов картофеля и сколько килограммов свёклы привезли в магазин? |
| Краткая запись условия | 120 кг |
| Разбор задачи | Аналитический способ разбора (от вопроса к данным): 1) Что известно в задаче? 2) Что нужно узнать в задаче? 3) Можем ли мы сразу ответить, сколько килограммов картофеля привезли в магазин? (Нет.) 4) Что для этого нужно узнать? (Массу одного ящика и количества ящиков.) 5) Количество ящиков известно, а как можно найти массу одного ящика? (Общую массу разделить на общее количество ящиков.) 6) Как найдём общее количество ящиков? (К 6 прибавим 4.) 7) Узнав массу одного ящика, как найдём массу всего картофеля? (Массу одного ящика умножим на количество ящиков с картофелем.) 8) Как узнать массу всей свёклы? (Массу одного ящика умножим на количество ящиков со свёклой.) 9) Как можно другим способом узнать массу всей свёклы? (Из общей массы вычесть массу картофеля.) |
| Запись решения | Запись решения по действиям с пояснением: 1) 6 + 4 = 10 (ящ.) – привезли всего. 2) 120: 10 = 12 (кг) – масса одного ящика. 3) 12 ∙ 6 = 72 (кг) – привезли картофеля. 4) 12 ∙ 4 = 48 (кг) – привезли свёклы. Ответ: 72 кг и 48 кг. |
| Закрепление:задания на составление задач данного вида с акцентированием на жизненную ситуацию. Решение задач на нахождение неизвестных по двум разностям В качестве подготовительных упражнений к ведению задач этого типа полезно предлагать задачи-вопросы и простые задачи повышенной трудности, которые помогут детям уяснить соответствие между двумя разностями, например: 1) Сестра купила 5 одинаковых тетрадей, а брат 8 таких же тетрадей. Кто из них больше уплатил денег? Почему? За сколько тетрадей брат уплатил столько же денег, сколько уплатила сестра? 2) Брат и сестра купили тетради по одинаковой цене. Брат купил на 3 тетради больше, чем сестра, и уплатил на 6 рублей больше, чем сестра. Сколько стоила 1 тетрадь? Выполняя предметную иллюстрацию, надо показать детям, что брат купил столько же тетрадей, сколько сестра, и ещё 3 тетради и уплатил денег столько же, сколько сестра, и ещё 6 рублей. Отсюда можно заключить, что 3 тетради стоят 6 рублей, значит, можно узнать, сколько стоит 1 тетрадь. Такие упражнения надо включать с различными группами пропорциональных величин. Методика работы по ознакомлению с задачами на нахождение неизвестных по двум разностям аналогична методике введения задач на пропорциональное деление. | |
| Вид задачи | На нахождение неизвестных по двум разностям |
| Условие | В магазин привезли 6 ящиков картофеля и 4 таких же ящика свёклы, причём картофеля привезли на 24 кг больше, чем свёклы. Сколько килограммов картофеля и сколько килограммов свёклы привезли в магазин? |
| Краткая запись условия | на 24 кг больше. Из этой наглядной записи хорошо видно, что 24 кг картофеля находится в 2 ящиках. |
| Разбор задачи | Синтетический способ разбора (от данных к вопросу): 1) Что известно в задаче? 2) Что нужно узнать в задаче? 3) Почему картофеля оказалось в магазине на 24 кг больше? (Потому, что ящиков с картофелем было больше.) 4) На сколько ящиков больше? (На 2.) 5) Какой вывод из этого можно сделать? (Что 24 кг картофеля находится в 2 ящиках.) 6) Зная это, как найти массу одного ящика с картофелем? (Нужно 24 кг разделить на 2.) 7) Как теперь найти массу картофеля и массу свёклы? (Массу одного ящика умножить на количество ящиков.) |
| Запись решения | Запись решения с предварительной постановкой вопросов: 1) На сколько ящиков картофеля привезли больше, чем свёклы? 6 – 4 = 2 (ящ.) 2) Какова масса одного ящика с овощами? 24: 2 = 12 (кг) 3) Сколько килограммов картофеля привезли в магазин? 12 ∙ 6 = 72 (кг) 4) Сколько килограммов картофеля привезли в магазин? 12 ∙ 4 = 48 (кг) Ответ: 72 кг картофеля и 48 кг свёклы. |
Проверка решения выполняется способом установления соответствия между числами, полученными в ответе, и данными в условии задачи: узнаем, действительно ли картофеля привезли на 24 кг больше чем свёклы: 72 – 48 = 24; значит, можно считать, что задача решена правильно.
Для закрепления умения решать задачи предлагаются:
Готовые задачина нахождение неизвестных по двум разностям I вида с различными группами пропорциональных величин и проводятся различные упражнения творческого характера;
Задачи на нахождение неизвестных по двум разностям II вида;
Упражнения на преобразование задач.
Задачи, связанные с движением , т. е. задачи с величинами: скорость, время, расстояние, рассматриваются в 4 классе.
Подготовительная работа к решению задач, связанных с движением, предусматривает обобщение представлений детей о движении, знакомство с новой величиной – скоростью, раскрытие связей между величинами: скорость, время, расстояние.
С целью обобщения представлений детей о движении полезно провести специальную экскурсию по наблюдению за движением транспорта, после чего провести наблюдение в условиях класса, где движение будут демонстрировать сами дети. На экскурсии и во время работы в классе пронаблюдать за движением одного тела и двух тел относительно друг друга. Так, одно тело (трамвай, машина, человек и т.п.) может двигаться быстрее имедленнее, может остановиться, может двигаться по прямой или кривой. Два тела могут двигаться в одном направлении, а могут двигаться в противоположных направлениях: либо приближаясь одно к другому (двигаясь навстречу одно к другому), либо удаляясь одно от другого. Наблюдая указанные ситуации в условиях класса, надо показать детям, как выполняются чертежи: расстояние принято обозначать отрезком; место (пункт) отправления, встречи, прибытия и т.п. обозначают либо точкой на отрезке и соответствующей буквой, либо чёрточкой, либо флажком; направление движения указывают стрелкой. Например, встречное движение двух тел изображается так:
А ├────────┼────────┤В
Здесь отрезок обозначает расстояние, которое должны пройти тела до встречи, флажок – место встречи, точки А и В – пункты выхода тел, стрелки – направление движения. Полезно выполнять и обратные упражнения: по данному чертежу выполнять соответствующее движение.
При ознакомлении со скоростью целесообразно так организовать работу, чтобы учащиеся нашли скорость своего движения пешком. Для этого можно начертить во дворе, в спортзале или коридоре «замкнутую дорожку». На дорожке надо отметить расстояния по 10 м, чтобы удобнее было находить, какой путь прошёл каждый ученик. Учитель предлагает детям идти по дорожке, например, в течение 4 мин. Учащиеся сами легко найдут по десятиметровым отметкам пройденное расстояние. На уроке каждый из детей может вычислить, какое расстояние он проходит за 1 мин. Учитель сообщает, что расстояние, которое прошёл ученик за минуту, называют его скоростью. Ученики называют свои скорости. Затем учитель называет скорости некоторых видов транспорта. Эти данные учащиеся могут записать в своих справочниках и использовать в дальнейшем при составлении задач.
Раскрытие связей между величинами : скорость – время – расстояние ведётся по такой же методике, как и раскрытие связей между другими пропорциональными величинами. В результате решения соответствующих простых задач ученики должны усвоить такие связи: если известны расстояние и время движения, то можно найти скорость действием деления; если известны скорость и время движения, то можно найти расстояние действием умножения; если известны расстояние и скорость, то можно найти время движения действием деления.
Далее, опираясь на эти знания, дети будут решать составные задачи, в том числе задачи на нахождение четвёртого пропорционального, на пропорциональное деление, на нахождение неизвестных по двум разностям с величинами: скорость, время, расстояние. При работе над этими задачами надо чаще использовать иллюстрации в виде чертежа, так как чертёж помогает правильно представить жизненную ситуацию, отражённую в задаче.
Так же как и при решении задач других видов, следует включать упражнения творческого характера на преобразование и составление задач.
Одновременно с решением задач названных видов в 4 классе вводятся задачи на встречное движение и движение в противоположных направлениях. Каждая из этих задач имеет три вида в зависимости от данных и искомого:
I вид – даны скорость каждого из тел и время движения, искомое – расстояние;
II вид – даны скорость каждого из тел и расстояние, искомое – время движения;
III вид – даны расстояние, время движения и скорость одного из тел, искомое – скорость другого тела.
В целях подготовки к введению задач на встречное движение очень важно сформировать правильные представления об одновременном движении двух тел: дети должны хорошо уяснить, что если два тела вышли одновременно навстречу друг другу, то до встречи они будут находиться в пути одинаковое время и при этом оба пройдут всё расстояние между пунктами, из которых они вышли. Чтобы дети осознали это, следует включать задачи-вопросы, аналогичные следующим:
1) Из двух городов одновременно отплыли навстречу друг другу два теплохода и встретились через 3 ч. Сколько времени был в пути до встречи каждый теплоход?
2) Из посёлка в город вышел пешеход и в это время из города навстречу ему выехал велосипедист, который встретил пешехода через 40 мин. Сколько времени был в пути до встречи пешеход?
Теперь можно ознакомить детей с решением задач на встречное движение, причём целесообразно на одном уроке ввести все три вида, получая новые задачи путём преобразования данной в обратные. Такой приём позволяет детям самостоятельно найти решение, поскольку задача нового вида будет получена из задачи, уже решённой детьми. Раскроем это на конкретном примере.
Учитель читает задачу: «Из двух поселков выехали одновременно навстречу друг другу два велосипедиста и встретились через 2 ч. Один ехал со скоростью 15 км в час, а второй со скоростью 18 км в час. Найти расстояние между поселками».
Что известно о движении велосипедистов? Что надо узнать? Пусть это будет посёлок, из которого выехал первый велосипедист. (Учитель вставляет в наборное полотно карточку с римской цифрой «I»). А это посёлок, из которого выехал второй велосипедист. (Вставляет карточку.) Двое из вас будут велосипедистами. (Выходят два ученика.) С какой скоростью ехал первый? (15 км в час.) Это твоя скорость. (Даёт карточку, на которой написано число 15.) Это твоя скорость. (Даёт второму ученику карточку.) Сколько времени они будут двигаться до встречи? (2 ч.) Начинайте двигаться. Прошел час. (Дети вставляют одновременно свои карточки в наборное полотно.) Прошёл второй час. (Дети вставляют карточки.) Встретились ли велосипедисты? (Да.) Почему? (Шли до встречи по 2 ч.) Обозначу место встречи флажком. (Вставляет флажок.) Что надо узнать? (Всё расстояние.) Обозначу вопросительным знаком. Получается иллюстрация:
| I |
| ? |
| II |
После такого разбора учащиеся сами находят два способа решения. Решения надо записать с пояснениями сначала отдельными действиями, а позднее можно записать выражение или уравнение.
Первый способ:
1) 35 ∙ 2 = 30 (км) – проехал первый велосипедист;
2) 18 ∙ 2 = 36 (км) – проехал второй велосипедист;
3) 30 + 36 = 66 (км) – расстояние между поселками.
Второй способ:
1) 15 + 18 = 33 (км) – сближались велосипедисты в час;
2) 33 ∙ 2 = 66 (км) – расстояние между поселками.
Если дети затруднятся в решении вторым способом, надо вновь проиллюстрировать движение: прошел час – сблизились на 33км, ещё час – ещё сблизились на 33 км, т.е. велосипедисты проехали 2раза по 33 км.
Учитель на доске, а дети в тетрадях выполняют чертёж к решённой задаче:
15км/ч 2 ч 18 км/ч
I ├────────┼────────┤II
Выясняется, который из велосипедистов прошёл до встречи большее расстояние и почему.
Учитель изменяет условие задачи, используя тот же чертёж:
15км/ч? ч 18 км/ч
I ├────────┼────────┤II
Дети составляют задачу по этому чертежу, затем задача коллективно разбирается, после чего записывается решение с пояснениями:
1) 15+18=33 (км) – сближались велосипедисты в час;
2) 66:33=2 (ч) – время движения до встречи.
Условие задачи ещё раз изменяется:
Км/ч 2 ч 18 км/ч
I ├────────┼────────┤II
Ученики составляют задачу, после чего коллективно разбираются два способа решения:
Первый способ:
1) 18 ∙ 2 = 36 (км) – проехал до встречи второй велосипедист;
2) 66 – 36 = 30 (км) – проехал до встречи первый велосипедист;
3) 30: 2 = 15 (км/ч) – скорость первого велосипедиста.
Ответ: 15 км в час.
Второй способ:
1) 66: 2 = 33 (км) – сближались велосипедисты в час;
2) 33 – 18 = 15 (км/ч) – скорость первого велосипедиста.
Ответ: 15 км в час.
На последующих уроках проводится работа по закреплению умения решать задачи рассмотренных видов. С этой целью включаются готовые задачи на встречное движение, при этом учащиеся сами выполняют чертёж, выясняя предварительно, ближе к какому пункту произойдёт встреча. Как и при работе над другими задачами, следует выполнять различные упражнения творческого характера.
Аналогичным образом ведётся работа над задачами на движение в противоположных направлениях.
Методика ознакомления с действием деление
Основы формирования у младших школьных представлений о смысле деления служит теоретико-множественный подход к трактовке частного, суть которого сведется к разбиению конечного множества на равномощные, попарно непересекающиеся подмножества. Такой подход более доступен учащимся, так как предполагает использование жизненного опыта ребенка по УМК школа России. Раскрытие смысла деления происходит через деление по содержанию.
«12 роз поставили в вазы, по 3 розы. Сколько потребовалось ваз? » Задача решается практически.
Задача решена, ответ найден, но записать решение ребенок не может.
Учитель говорит: Есть ли какие-то предметы деления на равные части, раскладывают поровну, то действие можно записать с помощью деления: 12:3=4(в). Показывает запись(:) и обозначение.
На следующем этапе рассматривается деление на равные части, через решение обратной задачи. Тип задачи такой: «12 роз поставили в 4 вазы поровну. Сколько роз в каждой вазе?»
Чтобы роз было поровну, будем ставить их по 1 в вазу. Для этого сразу возьмем 4 розы и так далее.
Данный фрагмент показывает связь деления на равные части с делением по содержанию. Деление на равные части включает в себя деление по содержанию, а именно деление по одному 12:4=3(р)
На отдельных уроках решаются два вида задач, задачи решаются практически или через схематических рисунок.
П: 12 кусков сахара нужно разложить по 3 в стаканы. Сколько потребуется стаканов? Решаем задачу практически(сахар, стаканы). В тетради делаем рисунок (схематически).
Замечание: у учащихся не должно сформироваться представление о том, что есть два действия деления. Они должны понимать: делим мы по содержанию или на равные части, но если делимое и делитель совпадают, то есть равны он частные будут равны.)
Ознакомление с компонентами деления происходили аналогично компонентам умножения.
Опираясь на смысл деления на действия с предметными множествами устанавливается взаимосвязь между компонентами и результатом деления. Учитель на доске располагает 8 по 2 и предлагает составить задачу на деление.
8:2=4 (делимое:делитель= частное)
Отсюда формулируется правила:
1.Чтобы найти делетиль, нужно делимое разделить на частное.
В четырех группах по 2.Сколько всего?
Из этого следует правило: чтобы найти делимое, нужно частное умножить на делитель.
Особые случаи деления:
1.Деление на 1. Зная, что 1*4=4 ,имеем 4:1=4- нахождение компонента умножения. Рассмотрев несколько таких случаев,делаем вывод: при деление числа на 1 получаем тоже самое число.
2.Деление на 10
20:10- это значит подобрать такое число, которое при умножении на 10=20. Это 2.
Значит найти такое число, при умножениии которого на 5 получим 0-это ноль. Рассмотрев несколько предметов, делаем вывод: при делении 0 на любое число, получается 0.
Задачи на пропорциональное деление
Эти задачи вводятся в 4 классе. Основным признаком задач на пропорциональное деление является содержащееся в задаче требование распределить одно численное значение величины (например, стоимости) соответственно данным числам (например, соответственно числу вещей в одной группе и числу вещей в другой группе).
| NN | Величины | Задачи | ||
| цена | количество | стоимость | ||
| Постоянная | Даны два или более значений | Дана сумма значений, соответствующих количеству. Найти слагаемые | Ученица купила по одинаковой цене 6 тетрадей в клетку и 4 тетради в линейку. Всего она уплатила 20 р. Сколько стоили тетради в клетку и в линейку в отдельности? | |
| Постоянная | Даны два или более значений | Ученица купила по одинаковой цене тетради в клетку и линейку, всего 10 штук. За тетради в клетку она уплатила 12 р. а за тетради в линейку 18 р. Сколько было куплено тетрадей в клетку и линейку в отдельности? | ||
| Даны два или более значений | Постоянное | Дана сумма значений, соответствующих цене. Найти слагаемые | В магазине продали одинаковое количество шапок и шарфов. Шапка стоила 50 р., а шарф 30 р. За все проданные вещи выручили 160 р. Сколько стоили все шапки и шарфы в отдельности? | |
| Дана сумма значений, соответствующих стоимости. Найти слагаемые | Постоянное | Даны два или более значений | В магазине продали одинаковое количество шапок и шарфов. Шапка с шарфом стоили 80 р. За все шапки выручили 100 р., а за все шарфы 60 р. Сколько стоили шапка и шарф в отдельности? |
Подготовкой к решению задач данного вида является умение решать задачи на нахождение четвертого пропорционального. Для ознакомления с задачами на пропорциональное деление в учебнике предлагается одновременно две задачи
1) Детям купили игрушки: Оле 6 одинаковых стульев, а Кате 4 таких же стула. Все стулья стоили 500 р. Сколько стоит 1 стул?
2) Детям купили: Оле 6 одинаковых стульев, а Кате 4 таких же стула. Все стулья стоили 500 р. Сколько стоят 6 стульев, купленных Оле, и сколько стоят 4 стула, купленных Кате?
1) Задача 645 (1) является подготовительной ко второй задаче. Ученики читают задачу и рассматривают рисунок в учебнике. После этого записывают задачу кратко под руководством учителя и решают устно.
Какие величины даны в задаче? (Цена, количество, стоимость.) Запишем. Что известно? (Количество стульев: Оле купили 6 одинаковых стульев, а Кате - 4 таких же стула; известна стоимость - все стулья стоили 500 р.) Что надо узнать? (Цену.) Что известно о цене? (Она одинаковая.) Запишем. Получается запись.
Можно ли сразу узнать цену стула? (Нет.) Почему? (Не знаем, сколько всего стульев купили.) А это можно узнать? (Можно.) Как решим эту задачу? (Сначала узнаем, сколько стульев купили: к 6 прибавим 4, получится 10. Купили 10 стульев. Теперь узнаем цену стула: разделим 500 на 10, получится 50. Цена стула - 50 р.)
Прочитайте задачу 645 (2) и скажите, чем она отличается от предыдущей. (Эта задача отличается вопросом: здесь надо узнать не цену стула, а стоимость 6 стульев и 4 стульев.) Запишем в краткой записи два вопросительных знака:
Здесь два вопроса задачи. Назовите их. (Сколько стоят 6 стульев и сколько стоят 4 стула.) Как узнать, сколько стоят 6 стульев? (Надо цену стула умножить на 6, а как находить цену, мы уже знаем.) Как же решить задачу? (Сначала узнаем, сколько купили всего стульев, затем цену стула, потом стоимость 6 стульев.) Нельзя ли теперь узнать стоимость 4 стульев? (Можно: цену стула умножить на 4.)
Эту первую задачу на пропорциональное деление полезно решить с записью отдельных действий и пояснений к ним или так называемых вопросов:
1) Сколько всего стульев купили?
2) Сколько стоит один стул?
3) Сколько стоят 6 стульев?
4) Сколько стоят 4 стула?
Проверка: 300+200=500 (р.)
Ответ: 6 стульев стоят 300 р., 4 стула - 200 р.
После усвоения таких рассуждений нужно научить учащихся применять для краткой записи чертеж (рис.80):

При первоначальном ознакомлении применять чертеж нецелесообразно, т.к. учащиеся усваивают формальные рассуждения: "считаем маленькие отрезки, (их 10), потом 500:10=5 и 5 6=30, 5 4=20", т.е. происходит преждевременное сокращение рассуждений. Разбор задачи изображать в виде графической схемы тоже нецелесообразно, т.к. она начнется с двух вопросов и вызывает затруднение учащихся.
Для закрепления решения задач на пропорциональное деление в дальнейшем включаются задачи с другими величинами и другие задачи из этой группы. Используются упражнения творческого характера на составление и преобразование задач.
19. Задачи на нахождение четвертого пропорционального
В задачах на нахождение четвертого пропорционального даются три величины, связанные с пропорциональной зависимостью (прямой, обратной) и, исходя из которых, находят четвертую, искомую величину. Эти четыре величины составляют пропорцию, отсюда и название этих задач.
Величинами в этих задачах могут быть цена, количество, стоимость; скорость, время, расстояние; масса одного предмета, количество предметов, общая масса и другие.
| Величины | Задачи | |||
| цена | количество | стоимость | ||
| Постоянная | Даны два значения | За 2 кг моркови уплатили 4 р. Сколько надо уплатить за 6 кг моркови по такой же цене? | ||
| Постоянная | Дано одно значение, а другое является искомым | Даны два значения | За 6 кг моркови уплатили 12 р. Сколько килограммов моркови по такой же цене можно купить на 4 руб. | |
| Даны два значения | Постоянное | Дано одно значение, а другое является искомым | За кусок льняного полотна ценой по 20 р. за метр уплатили 80 р. Сколько уплатят за кусок шелкового полотна такой же длины, если его цена 40 р. за метр? | |
| Дано одно значение, а другое является искомым | Постоянное | Даны два значения | За кусок шелкового полотна ценой по 40 р. за метр уплатили 160 р., а за кусок льняного полотна такой же длины уплатили 80 р. По какой цене покупали льняное полотно? | |
| Даны два значения | Дано одно значение, а другое является искомым | Постоянная | За 6 детских костюмов ценой по 120 р. уплатили столько же, сколько за детские пальто ценой по 360 р. Сколько купили детских пальто? | |
| Дано одно значение, а другое является искомым | Даны два значения | Постоянная | За 2 детских пальто ценой по 360 р. уплатили столько же, сколько за 6 детских костюмов. По какой цене покупали костюмы? |
Подготовительная работа к решению задач на нахождение четвертого пропорционального с величинами цена, количество и стоимость начинается с ознакомления со связью между ними. Это можно провести через игру в "магазине" (прием М.И. Моро, М.А. Бантовой).
На доску прикрепляются "товары": тетради, карандаши, блокноты и т.д. На них обозначены цены (прикреплены этикетки: "Цена 3 руб.", "Цена 5 руб." и т.д.).
Сегодня будем играть в "магазин" и решать задачи о покупках. Вот это магазин. (Показывает на доску.) Что продается в магазине? (Называют.) На вещах обозначена цена. Назовите цену тетради. (3 руб.) Цену блокнота. (5 руб.) Что же показывает цена? (Сколько стоит 1 тетрадь, 1 блокнот и т.д.) Я куплю 3 тетради. Что обозначает число 3? (Сколько вы купили тетрадей.) Иначе говорят: это число тетрадей, или количество тетрадей. Я купила 8 блокнотов. Что обозначает число 8? (Число блокнотов или количество блокнотов.) Сколько денег я должна уплатить за 2 блокнота? (10 руб.) Как вы узнали? (5 2=10.) 10 руб. – это стоимость 2 блокнотов.
На доске в таблице учитель записывает:
Далее один из учеников назначается продавцом, а несколько учеников - покупателями. Покупатели по очереди подходят к продавцу и покупают несколько вещей. Ученики из класса составляют задачи на эти покупки, решают их и записывают в таблице. После решения 2-3 задач учащиеся делают вывод: если известны цена и количество, то можно найти стоимость, умножив цену на количество.
На других уроках решаются простые задачи на нахождение цены, количества по известным двум другим величинам. Для работы у доски учителю очень удобна опорная схема
При ознакомлении с задачами данного вида учителю сразу следует начинать приучать учащихся к разбору от вопроса к числовым данным, используя графическую схему. В задаче 1 таблицы это выглядит так

Запись решения таких вначале выполняется по действиям с пояснениями, а после по указанию учителя.
При закреплении решения этих задач полезно показать и другой способ их решения (через коэффициент пропорциональности - термин учащимся не сообщается). Для закрепления далее постепенно вводятся аналогичные задачи с другими величинами. Используются различные ранее рассмотренные нами приемы закрепления.