Одним из видов функциональных рядов является тригонометрический ряд
Ставится задача подобрать коэффициенты ряда так, чтобы он сходился к заданной в интервале [-π, π] функции; иначе говоря, требуется разложить данную функцию в тригонометрический ряд. Достаточное условие разрешимости этой задачи состоит в том, чтобы функция была в интервале [-π, π] кусочно-непрерывна и кусочно-дифференцируема, т. е. чтобы интервал [-π, π] мог быть разбит на конечное число частичных интервалов, в каждом из которых данная функция непрерывна и имеет производную (на концах частичных интервалов функция должна иметь конечные односторонние пределы и односторонние производные, при вычислении которых в качестве значения функции в конце частичного интервала берется ее односторонний предел). Условие кусочной дифференцируемости может быть заменено условием кусочной монотонности функции, т. е. требованием, чтобы в каждом из частичных интервалов функция была монотонна. Достаточным условием разложимости функции в интервале [-π, π] в тригонометрический ряд является также требование, чтобы в этом интервале функция имела ограниченное изменение. По определению функции f(x) имеет в интервале ограниченное изменение, если при любом разбиении этого интервала на конечное число интервалов
величина
ограничена сверху одним и тем же числом.
Именно с такими функциями приходится иметь дело при решении практических задач.
При выполнении любого из трех указанных достаточных условий функция f(x) представляется в интервале [-π, π] тригонометрическим рядом, у которого коэффициенты определяются по формулам
При таких коэффициентах тригонометрический ряд называется рядом Фурье . Этот ряд сходится к f(x) в каждой точке ее непрерывности; в точках разрыва он сходится к среднему арифметическому левого и правого предельных значений, т. е. k , если х есть точка разрыва (рис. 1); на границах отрезка ряд сходится к .
Рисунок 1.
Функция, выражаемая рядом Фурье, есть функция периодическая, а потому ряд, составленный для функции, заданной на отрезке [-π, π], сходится вне этого отрезка к периодическому продолжению этой функции (рис. 2).
Рисунок 2.
Если рядом Фурье представляется функция f(x), заданная в произвольном интервале [α, α+2π] длиной 2π, то коэффициенты ряда а 0 , a k , b k (коэффициенты Фурье) можно определить по указанным формулам, в которых пределы интегрирования заменены на α и α+2π. Вообще, поскольку в формулах для а 0 , a k , b к стоят функции с периодом 2π, интегрирование можно проводить по любому интервалу с длиной 2π.
Ряд Фурье может быть использован для приближенного представления функции, а именно: функция f(x) заменяется приближенно равной ей суммой s n (x) первых нескольких членов ряда Фурье:
Выражение s n (x), где а 0 , a k , b k являются коэффициентами Фурье функции f(x), по сравнению с другими выражениями такого же вида с тем же значением n, но с другими коэффициентами, приводит к минимальному среднему квадратичному отклонению s n (x) от f(х), которое определяется как
В зависимости от рода симметрии функции возможны некоторые упрощения. Если функция четная, т. е. f(-x)=f(x), то
и функция разлагается в ряд по косинусам. Если функция нечетная, т. е. f(-х)=-f(x), то
и функция разлагается в ряд по синусам. Если функция удовлетворяет условию f(x+π)=-f(x), т. е. кривая, относящаяся к половине отрезка длиной 2π, является зеркальным отражением другой половины кривой, то
Функция может быть задана не только на отрезке длиной 2π, но также на отрезке любой длины 2l. Если она на этом отрезке удовлетворяет приведенным выше условиям, то она разложима в ряд Фурье следующего вида:
причем коэффициенты ряда вычисляются по формулам
В табл. 1 даны разложения некоторых функций.
Таблица 1.
Тригонометрический ряд можно записать и в таком виде:
Ряд Фурье функции f(x) сходится тем скорее, чем более гладкой является функция. Если функция f(x) и ее производные f"(x), f"(x), ..., f k -1 (x) всюду непрерывны, а f (k) (x) допускает лишь точки разрыва 1-го рода в конечном числе, то коэффициенты Фурье а n , b n функции f(х) будут
Символом обозначается такая величина, что
Разложение в тригонометрический ряд называют гармоническим анализом, а тригонометрические функции, входящие в этот ряд, - гармониками. Вычисление по составляющим гармоникам называется гармоническим синтезом.
При расчетах конструкций часто приходится разлагать в ряд Фурье различные функции, заданные графиками, и прежде всего изображающие нагрузку. В табл. 2 и 3 даны разложения для некоторых функций, характерных для нагрузок, в том числе и ряды, соответствующие сосредоточенным силам.
Таблица 2.
График функций |
Ряд Фурье |
n |
2. Определение коэффициентов ряда по формулам Фурье.
Пусть периодическая функция ƒ(х) с периодом 2π такая, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале (-π, π), т. е. является суммой этого ряда:
Предположим, что интеграл от функции, стоящей в левой части этого равенства, равняется сумме интегралов от членов этого ряда. Это будет выполняться, если предположить, что числовой ряд, составленный из коэффициентов данного тригонометрического ряда, абсолютно сходится, т. е.. сходится положительный числовой ряд
Ряд (1) мажорируем и его можно почленно интегрировать в промежутке (-π, π). Проинтегрируем обе части равенства (2):
Вычислим отдельно каждый интеграл, встречающийся в правой части:
 ,
,
 ,
,
Таким образом,  , откуда
, откуда
 . (4)
. (4)
Оценка коэффициентов Фурье. (Бугров)
Теорема 1. Пусть функция ƒ(x) периода 2π имеет непрерывную производную ƒ (s) (x) порядка s, удовлетворяющей на всей действительной оси неравенству:
│ ƒ (s) (x)│≤ M s ; (5)
тогда коэффициенты Фурье функции ƒ удовлетворяют неравенству
Доказательство. Интегрируя по частям и учитывая, что
ƒ(-π) = ƒ(π), имеем


Интегрируя правую часть (7) последовательно, учитывая, что производные ƒ ΄ , …, ƒ (s-1) непрерывны и принимают одинаковые значения в точках t = -π и t = π, а также оценку (5), получим первую оценку (6).
Вторая оценка (6) получается подобным образом.
Теорема 2. Для коэффициентов Фурье ƒ(x) имеет место неравенство
 (8)
(8)
Доказательство. Имеем
 (9)
(9)
Вводя в данном случае замену переменной и учитывая, что ƒ(x) – периодическая функция, получим

Складывая (9) и (10), получаем


Аналогичным образом проводим доказательство для b k .
Следствие. Если функция ƒ(x) непрерывна, то её коэффициенты Фурье стремятся к нулю: a k → 0, b k → 0, k → ∞.
Пространство функций со скалярным произведением.
Функция ƒ(x) называется кусочно-непрерывной на отрезке , если она непрерывна на этом отрезке, за исключением, может быть, конечного числа точек, где она имеет разрывы первого рода. Такие точки можно складывать и умножать на действительные числа и получать как результат снова кусочно-непрерывные на отрезке функции.
Скалярным произведением двух кусочно-непрерывных на (a < b) функций ƒ и φ будем называть интеграл
 (11)
(11)
Очевидно для любых кусочно-непрерывных на функций ƒ , φ , ψ выполняются свойства:
1) (ƒ , φ) =(φ, ƒ);
2) (ƒ , ƒ) и из равенства (ƒ , ƒ) = 0 следует, что ƒ(x) =0 на , исключая, быть может, конечное число точек x;
3) (α ƒ + β φ , ψ) = α (ƒ , ψ) + β (φ , ψ),
где α, β – произвольные действительные числа.
Множество всех кусочно-непрерывных функций, определенных на отрезке , для которых введено скалярное произведение по формуле (11), мы будем обозначать, ![]() и называть пространством
и называть пространством ![]()
Замечание 1.
В математике называют пространством = (a, b) совокупность функций ƒ(x), интегрируемых в лебеговом смысле на вместе со своими квадратами, для которых введено скалярное произведение по формуле (11). Рассматриваемое пространство есть часть . Пространство обладает многими свойствами пространства , но не всеми.
Из свойств 1), 2), 3) следует важное неравенство Буняковского | (ƒ , φ) | ≤ (ƒ , ƒ) ½ (φ , φ) ½ , которое на языке интегралов выглядит так:

Величина

называется нормой функции f.
Норма обладает следующими свойствами:
1) || f || ≥ 0, при этом равенство может быть только для нулевой функции f = 0, т. е. функции, равной нулю, за исключением, быть может, конечного числа точек;
2) || ƒ + φ || ≤ || ƒ(x) || || φ ||;
3) || α ƒ || = | α | · || ƒ ||,
где α – действительное число.
Второе свойство на языке интегралов выглядит так:

и называется неравенством Минковского.
Говорят, что последовательность функций { f n }, принадлежит к ,сходится к функции принадлежит в смысле среднего квадратического на (или ещё по норме ), если

Отметим, что если последовательность функций ƒ n (x) сходится равномерно к функции ƒ(x) на отрезке , то для достаточно больших n разность ƒ(x) - ƒ n (x) по абсолютной величине должна быть мала для всех х из отрезка .
В случае же, если ƒ n (x) стремится к ƒ(x)в смысле среднего квадратического на отрезке , то указанная разность может и не быть малой для больших n всюду на . В отдельных местах отрезка эта разность может быть и велика, но важно только, чтобы интеграл от её квадрата по отрезку был мал для больших n.
Пример. Пусть на заданна изображенная на рисунке непрерывная кусочно-линейная функция ƒ n (x) (n = 1, 2,…), причем


(Бугров, стр. 281, рис. 120)
При любом натуральном n
![]()
и, следовательно, эта последовательность функций, хотя и сходится к нулю при n → ∞, но неравномерно. Между тем


т. е. последовательность функций {f n (х)} стремится к нулю в смысле среднего квадратического на .
Из элементов некоторой последовательности функций ƒ 1 , ƒ 2 , ƒ 3 ,… (принадлежащих ) построим ряд
ƒ 1 + ƒ 2 + ƒ 3 +… (12)
Сумма первых его n членов
σ n = ƒ 1 + ƒ 2 + … + ƒ n
есть функция, принадлежащая к . Если случится, что в существует функция ƒ такая, что
|| ƒ- σ n || → 0 (n → ∞),
то говорят, что ряд (12) сходится к функции ƒ в смысле среднего квадратического и пишут
ƒ = ƒ 1 + ƒ 2 + ƒ 3 +…
Замечание 2.
Можно рассматривать пространство = (a, b) комплекснозначных функций ƒ(x) = ƒ 1 (x) + iƒ 2 (x), где ƒ 1 (x) и ƒ 2 (x) – действительные кусочно – непрерывные на функции. В этом пространстве функции умножаются на комплексные числа и скалярное произведение функций ƒ(x) = ƒ 1 (x) + iƒ 2 (x) и φ(х) = φ 1 (х) +i φ 2 (х) определяется следующим образом:

а норма ƒ определяется как величина
Ряд Фурье периодических функций с периодом 2π.
Ряд Фурье позволяет изучать периодические функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны - это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
где a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. - действительные константы, т.е.
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

Коэффициенты a o ,a n и b n называются коэффициентами Фурье , и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a 1 cosx+b 1 sinx) называется первой или основной гармоникой,
Другой способ записи ряда - использование соотношения acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Где a o - константа, с 1 =(a 1 2 +b 1 2) 1/2 , с n =(a n 2 +b n 2) 1/2 - амплитуды различных компонент, а равен a n =arctg a n /b n .
Для ряда (1) член (a 1 cosx+b 1 sinx) или c 1 sin(x+α 1) называется первой или основной гармоникой, (a 2 cos2x+b 2 sin2x) или c 2 sin(2x+α 2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π.
Разложение непериодических функций.
Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.
Говорят, функция y=f(x) четная , если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х 2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.
Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

где коэффициенты ряда Фурье,

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,

где коэффициенты ряда Фурье,
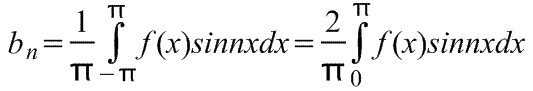
Ряд Фурье на полупериоде.
Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a o и a n


Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

Ряд Фурье для произвольного интервала.
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.
Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде .
Разложение по косинусам в диапазоне от 0 до L имеет вид

Функция , определённая при всех значениях x называется периодической , если существует такое число T (T≠ 0) , что при любом значении x выполняется равенство f(x + T) = f(x) . Число T в этом случае является периодом функции.
Свойства периодических функций :
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т.
2) Если функция f(x) имеет период Т ,то функция f(ax) имеет период
В самом деле, для любого аргумента х :
(умножение аргумента на число означает сжатие или растяжение графика этой функции вдоль оси ОХ )
Например, функция имеет период , периодом функции является
3) Если f(x) периодическая функция периода Т , то равны любые два интеграла от этой функции, взятые по промежутку длины Т (при этом предполагается, что эти интегралы существуют).
Ряд Фурье для функции с периодом T= .
Тригонометрическим рядом называется ряд вида:
или, короче,
Где , , , , , … , , , … - действительные числа, называемые коэффициентами ряда.
Каждое слагаемое тригонометрического ряда является периодической функцией периода (т.к. - имеет любой
период, а период () равен , а значит, и ). Каждое слагаемое (), при n= 1,2,3… является аналитическим выражением простого гармонического колебания , где A - амплитуда,
Начальная фаза. Учитывая сказанное, получаем: если тригонометрический ряд сходится на отрезке длины периода , то он сходится на всей числовой оси и его сумма является периодической функцией периода .
Пусть тригонометрический ряд равномерно сходится на отрезке (следовательно, и на любом отрезке) и его сумма равна . Для определения коэффициентов этого ряда воспользуемся следующими равенствами:
А так же воспользуемся следующими свойствами.
1) Как известно, сумма равномерно сходящегося на некотором отрезке ряда, составленного из непрерывных функций, сама является непрерывной функцией на этом отрезке. Учитывая это, получим, что сумма равномерно сходящегося на отрезке тригонометрического ряда - непрерывная функция на всей числовой оси.
2) Равномерная сходимость ряда на отрезке не нарушится, если все члены ряда умножить на функцию , непрерывную на этом отрезке.
В частности, равномерная сходимость на отрезке данного тригонометрического ряда не нарушится, если все члены ряда умножить на или на .
По условию
В результате почленного интегрирования равномерно сходящегося ряда (4.2) и учитывая вышеприведенные равенства (4.1) (ортогональность тригонометрических функций), получим:
Следовательно, коэффициент
Умножая равенство (4.2) на , интегрируя это равенство в пределах от до и, учитывая вышеприведенные выражения (4.1), получим:
Следовательно, коэффициент
Аналогично, умножая равенство (4.2) на и интегрируя его в пределах от до , с учетом равенств (4.1) имеем:
Следовательно, коэффициент
Таким образом, получены следующие выражения для коэффициентов ряда Фурье:
Достаточные признаки разложимости функции в ряд Фурье. Напомним, что точку x o разрыва функции f(x) называют точкой разрыва первого рода, если существуют конечные пределы справа и слева функции f(x) в окрестности точки.
Предел справа,
Предел слева.
Теорема (Дирихле). Если функция f(x) имеет период и на отрезке непрерывна или имеет конечное число точек разрыва первого рода и, кроме того, отрезок можно разбить на конечное число отрезков так, что внутри каждого из них f(x) монотонна, то ряд Фурье для функции f(x) сходится при всех значениях x . Причём в точках непрерывности функции f(x) его сумма равна f(x) , а в точках разрыва функции f(x) его сумма равна , т.е. среднему арифметическому предельных значений слева и справа. Кроме того, ряд Фурье для функции f(x) сходится равномерно на любом отрезке, который вместе со своими концами принадлежит интервалу непрерывности функции f(x) .
Пример : разложить в ряд Фурье функцию
Удовлетворяющую условию .
Решение. Функция f(x) удовлетворяет условиям разложимости в ряд Фурье, поэтому можно записать:
В соответствии с формулами (4.3) , можно получить следующие значения коэффициентов ряда Фурье:
При вычислении коэффициентов ряда Фурье использовалась формула «интегрирования по частям».
И, следовательно,
Ряды Фурье для чётных и нечётных функций с периодом T = .
Используем следующее свойство интеграла по симметричному относительно x=0 промежутку:
Если f(x) - нечётная функция,
если f(x) - чётная функция.
Заметим, что произведение двух чётных или двух нечётных функций - чётная функция, а произведение чётной функции на нечётную функцию - нечётная функция. Пусть теперь f(x) - чётная периодическая функция с периодом , удовлетворяющая условиям разложимости в ряд Фурье. Тогда, используя вышеуказанное свойство интегралов, получим:
Таким образом, ряд Фурье для чётной функции содержит только чётные функции - косинусы и записывается так:
а коэффициенты bn = 0.
Рассуждая аналогично, получаем, что если f(x) - нечётная периодическая функция, удовлетворяющая условиям разложимости в ряд Фурье, то, следовательно, ряд Фурье для функции нечётной содержит только нечётные функции - синусы и записывается следующим образом:
при этом an =0 при n= 0, 1,…
Пример: разложить в ряд Фурье периодическую функцию
Так как заданная нечетная функция f(x) удовлетворяет условиям разложимости в ряд Фурье, то
или, что то же,
И ряд Фурье для данной функции f(x) можнозаписать так:
Ряды Фурье для функций любого периода T=2l .
Пусть f(x) - периодическая функция любого периода T=2l (l- полупериод), кусочно-гладкая или кусочно-монотонная на отрезке [-l, l ]. Полагая x=at, получим функцию f(at) аргумента t, период которой равен . Подберём а так, чтобы период функции f(at) был равен , т.е. T = 2l
Решение. Функция f(x) - нечётная, удовлетворяющая условиям разложимости в ряд Фурье, поэтому на основании формул (4.12) и (4.13) имеем:
(при вычислении интеграла использовали формулу «интегрирования по частям»).
следует:1) нарисовать график f(x) на промежутке хотя бы длиной в два периода, чтобы показать, что данная функция периодическая;
2) нарисовать график S(x) аналогично, чтобы было видно в каких точках f(x)¹S(x);
3) вычислить коэффициенты Фурье и записать ряд Фурье.
Задачи
№1. Разложить в ряд Фурье
Решение. Заметим, что f(x) задана на промежутке длины T = 4 . Т.к. f(x) предполагается периодической, то именно это число и является ее периодом, тогда -l = 2.
1) График f(x) :
2) График S(x):
Стрелки в концах линий показывают, что функция не принимает в концах интервала значения, определяемого из выражения, заданного на интервале. При сравнении графиков f(x) и S(x) хорошо видно, что в точках разрыва f(x)¹S(x) .
3) Вычислим коэффициенты Фурье. Это можно сделать по формулам (3*): ; ; . Именно: ; итак,
Разложение f(x) в ряд Фурье имеет вид:
Замечания . 1) При интегрировании на [-1;3] этот отрезок был разбит на и , т.к. на этих отрезках f(x) задана разными значениями.
2) При вычислении коэффициентов использованы интегралы: и , где a = const .
№2 . Разложить в ряд Фурье
Решение. Здесь T = 2 , l = 1 .
Ряд Фурье имеет вид: , где ; ; , т.к. l = 1 .
1) График f(x) :
2) График S(x) :
№3. Разложить в ряд Фурье по синусам
Решение. Заметим, что в ряд Фурье по синусам раскладываются только нечетные функции. Т.к. f(x) определена только для x > 0, xÎ(0;2)È(2;3) , то это означает, что на симметричный промежуток (-3;-2)È(-2;0) f(x) нужно продолжить так, чтобы выполнялось равенство f(-x) = -f(x) . Поэтому длина промежутка, на котором f(x) задана как нечетная функция, равна 6. Значит T = 6, l = 3. Ряд Фурье для f(x) имеет вид: , где , n = 1, 2, 3, (по формулам (5")).
1) График f(x) .
Чтобы нарисовать график f(x) как нечетной функции, нарисуем сначала график на (0;2)È(2;3) , а затем воспользуемся тем, что график нечетной функции симметричен относительно начала координат. Из этих соображений получаем график f(x) на (-3;-2)È(-2;0) . Затем продолжаем f(x) T = 6 .
2) График S(x) .
График S(x) отличается от графика f(x) в точках разрыва функции f(x) . Например, в т. x = 2 f(x) не определена, а S(x) имеет при x = 2 значение, равное полусумме односторонних пределов функции f(x) , именно: , где , .
Итак, , тогда разложение f(x) в ряд Фурье имеет вид: .
№4 . Разложить в ряд Фурье по косинусам .
Решение . Заметим, что в ряд Фурье по косинусам раскладываются только четные функции. Т.к. f(x) задана только для x>0, xÎ(0;2)È(2;3], то это означает, что на симметричный промежуток [-3;-2)È(-2;0) f(x) нужно продолжить так, чтобы выполнялось равенство: f(-x) = f(x). Поэтому длина промежутка, на котором f(x) задана как четная функция, равна 6, тогда T = 6, l = 3. Ряд Фурье в этом случае имеет вид:
где ; ; n = 1,2,... (по формулам (4")).
1) График f(x) .
Чтобы нарисовать график f(x) как четной функции, нарисуем сначала график f(x) на (0;2)È(2;3] , а затем воспользуемся тем, что график четной функции симметричен относительно оси ординат. Из этих соображений получаем график f(x) на [-3;-2)È(-2;0) . Затем продолжаем f(x) на всю числовую прямую как периодическую функцию с периодом T = 6 .
Здесь график f(x) нарисован на двух полных периодах функции.
2) График S(x).
График S(x) отличается от графика f(x) в точках разрыва функции f(x) . Например, в т. x = 0 f(x) не определена, а S(x) имеет значение: , поэтому график S(x) не прерывается в т. x = 0 , в отличие от графика f(x) .
Разложение f(x) в ряд Фурье по косинусам имеет вид: .
№5. Разложить в ряд Фурье f(x) = |x|, xÎ(-2;2). .
Решение. По условию, f(x) является четной функцией на (-2;2) ; т.е. ее ряд Фурье содержит только косинусы, при этом T = 4, l = 2, ,
где ; ; n = 1, 2,
1) График f(x) :
2) График S(x) :
3) , т.к. |x| = x для x > 0. ; .
Тогда разложение f(x) в ряд Фурье имеет вид: . Заметим, что при интегрировании выражений или применяется формула интегрирования по частям: , где u = x; dv = cos(ax)dx или dv = sin(ax)dx.
№6. Разложить функцию в ряд Фурье: а) в интервале (-?, ?); б) в интервале (0, 2?); в) в интервале (0, ?) в ряд синусов.
Решение. а) График функции с 2? - периодическим продолжением имеет вид
Функция удовлетворяет условиям теоремы Дирихле и потому ее можно разложить в ряд Фурье.
Вычислим коэффициенты Фурье. Так как функция четная, то bn = 0 (n = 0, 1, 2,…) и (n = 0, 1, 2,…).
Для вычисления этого интеграла применяют формулу интегрирования по частям в определенном интеграле. Получаем
Ряд Фурье данной функции имеет вид . В силу признака Дирихле данный ряд представляет функцию х2 в интервале (-?,?).
б) Интервал (0, 2?) не симметричен относительно начала координат, а длина его 2l = 2?. Вычисляем коэффициенты Фурье по формулам:
Поэтому ряд Фурье имеет вид . В силу теоремы Дирихле ряд сходится к порождающей функции в точках х?(0,2?), а в точках 0 и 2? к значению. График суммы ряда имеет вид
в) Функция, разлагаемая в ряд по синусам, должна быть нечетной. Следовательно, доопределим заданную функцию х2 в (-π,π) нечетным образом, т.е. рассматриваем функцию . Для этой функции f(x) имеем аn = 0 (n = 0, 1, 2,…) и
Искомое разложение имеет вид .
График суммы ряда имеет вид
Отметим, что в точках х = (-π,π) ряд Фурье сходится к нулю.
№7 Разложить в ряд Фурье функцию, заданную графически:
Решение. Получим явное выражение для f(x). График функции - прямая линия, используем уравнение прямой в виде . Как видно из чертежа, , т.е. f(x) = x - 1 (-1 < x < 1) и период Т = 2.
Эта функция удовлетворяет условиям признака Дирихле, поэтому она разлагается в ряд Фурье. Вычислим коэффициенты Фурье (l = 1):
; (n = 1, 2,…);
Ряд Фурье для функции f(x) имеет вид
Он представляет функцию f(x) при -1 < x < 1, а в точках х0 = -1 и х0 = 1 ряд сходится к -1.
№8. Разложить функцию в тригонометрический ряд Фурье на отрезке и указать функцию, к которой сходится полученный ряд.
Решение. Нарисовать график функции, продолжив ее периодически с периодом или на всю ось. Продолженная функция имеет период .
Проверить условия достаточных признаков сходимости ряда Фурье (Дини-Липшица, Жордана, Дирихле).
Функция кусочно-монотонна на отрезке : она возрастает на и на . В точках функция имеет разрывы первого рода.
Выяснить четность или нечетность функции: Функция не является ни четной, ни нечетной.
а) если функция задана на
б) если функция задана на
Составить ряд Фурье функции : .
Указать функцию, к которой будет сходиться этот ряд, пользуясь поточечными признаками сходимости: Согласно признаку Дирихле ряд Фурье функции сходится к сумме:
№9. Разложить функцию , в ряд Фурье по синусам на и с помощью этого разложения найти сумму числового ряда .
Решение. Продолжить функцию четным (нечетным) образом на (-p ,0) или (-l ,0), а затем периодически с периодом 2p или 2l продолжить функцию на всю ось.
Продолжим функцию нечетным образом на , а затем периодически, с периодом , продолжим ее на всю ось.
Нарисовать график периодического продолжения. Мы получим функцию вида:
Проверить условия достаточных признаков сходимости ряда Фурье (Дини-Липица, Жордана, Дирихле).
Функция кусочно-постоянна в промежутке : она равна -1 на и 1 на . В точках функция имеет разрывы первого рода.
Вычислить коэффициенты Фурье:
Ее коэффициенты Фурье вычисляются по формулам:
Составить ряд Фурье функции . .
Указать функцию, к которой будет сходиться этот ряд, пользуясь поточечными признаками сходимости.
Согласно признаку Дирихле ряд Фурье функции сходится к сумме:
Следовательно, при
Подставив значения , указать сумму заданного числового ряда.
Полагая в полученном разложении , найдем ,
откуда, так как , .
№10. Написать равенство Парсеваля для функции , и, исходя из этого равенства, найти сумму числового ряда .
Решение. Установить, является ли данная функция функцией с интегрируемым квадратом на .
Функция непрерывна, а, следовательно, интегрируема на . По той же причине ее квадрат интегрируем на .
Вычислить коэффициенты Фурье по формулам:
Так как нечетная функция, то ее коэффициенты Фурье вычисляются по формулам:
Вычислить интеграл .
Написать формулу Парсеваля:
Таким образом, формула Парсеваля имеет вид
Произведя, если требуется, арифметические действия в правой и левой частях, получить сумму данного числового ряда.
Разделив обе части полученного равенства на 144, найдем: .
№11. Найти интеграл Фурье функции
и построить его график.
Решение. Построить график функции .
Проверить выполнение условий достаточных признаков сходимости интеграла Фурье (Дини, Дирихле-Жордана или следствий из них).
Функция абсолютно интегрируема в промежутке, непрерывна при и , а в точке имеет разрыв первого рода. Далее, при и функция имеет конечную производную, а в нуле существуют конечные правая и левая производные. Выяснить четность или нечетность функции. Функция не является ни четной, ни нечетной. ; .
Итак, , или ,









