Лекция 14 Случайные процессы Каноническое разложение случайных процессов. Спектральное разложение стационарного случайного процесса. СлуЛекция 14
Случайные процессы
Каноническое разложение случайных процессов.
Спектральное разложение стационарного случайного
процесса. Случайные процессы с независимыми
сечениями. Марковские процессы и цепи Маркова.
Нормальные случайные процессы. Периодически
нестационарные случайные процессы
(Ахметов С.К.)

Каноническое разложение случайных процессов

Любой СП X(t) м.б. представлен в
виде его разложения, т.е. в виде суммы
элементарных процессов:
Vk – случайные величины
φk(t) – неслучайные функции (синусоиды, экспоненты, степенные
функции и т.д)
Частный случай такого разложения-Каноническое
разложение
СП X(t), имеющее вид
mx(t) = M – математическое ожидание СП X(t)
V1, V2…Vk – некоррелированные и центрированные СВ
D1, D2 …Dk- дисперсии СВ V1, V2…Vk
φk(t) – неслучайные функции аргумента t
Случайные величины V1, V2…Vk называются коэффициентами канонического
разложения,
а неслучайные функции φ1(t), φ2(t) φk(t) - координатными функциями
канонического разложения

Основные характеристики СП, заданного каноническим разложением

M – математическое ожидание СП X(t)
Kx(t,t’) – корреляционная функция СП X(t)
Выражение
- каноническое разложение корреляционной
функции
Если t=t’, то в соответствие с первым
свойством корреляционной функции
Выражение
Dk(t) –
дисперсия
каноническое разложение дисперсии СП X(t)

Спектральное разложение стационарного СП

Стационарный СП м.б. представлен каноническим разложением
Vk и Uk – некоррелированные и центрированные СВ с дисперсиями
D = D = Dk
ω – неслучайная величина (частота)
В этом случае каноническое разложение корреляционной функции
определяется выражением
Представленное
каноническое
разложение
СП
X(t)
называется
спектральным разложением СП и
выражается в виде
Θk - фаза гармонического колебания элементарного стационарного СП,
являющаяся СВ равномерно распределенной в интервале (0, 2π);
Zk – СВ, представляющая собой амплитуду гармонического колебания
элементарного стационарного СП

Спектральное разложение стационарного СП (2)

Случайные величины Θk и Zk зависимы и для них справедливо:
Vk = Zk cos Θk
Uk = Zk sin Θk
Стационарный СП м.б. представлен в виде суммы гармонических
колебаний со случайными амплитудами Zk и случайными фазами Θk на
различных неслучайных частотах ωk
Корреляционная функция стационарного СП X(t) является четной
функцией своего аргумента, т.е. kx(τ) = kx(-τ). Поэтому ее на интервале (-Т,
Т) можно разложить в ряд Фурье по четным (косинусам) гармоникам:
Дисперсия стационарного СП X(t) равна
сумме
дисперсий
всех
гармоник
его
спектрального разложения
Зависимость Dk = f(wk) называется дискретным спектром дисперсий или
дискретным спектром стационарного СП.

Спектральное разложение стационарного СП (3)

При ∆ω
→ 0 произойдет переход к непрерывному спектру
Sx(ω) - спектральная плотность
Таким образом, корреляционная функция и спектральная плотность
связаны косинус – преобразованием Фурье. Следовательно, спектральная
плотность стационарного СП м.б. выражена через корреляционную
функцию формулой

Случайные процессы с независимыми сечениями

В гидрологии считается, что ряд соответствует модели случайной
величины, если отсутствует значимая корреляция между членами этого ряда
при любом сдвиге τ.
Случайный процесс с независимыми сечениями – это СП, для которого
при значениях t и t’
mx(t) = mx
Dx (t) = Dx
Kx(t,t’) = kx(τ) = {Dx при τ = 0 и 0 при τ ≠ 0}
Такой процесс является стационарным и обладает эргодическим
свойством
Для таких процессов характеристики одномерного закона распределения
можно оценить как по любому сечению, так и по любой (достаточно
продолжительной) реализации
У таких процессов отсутствует корреляция между членами внутри любой
реализации
Принимая такую модель, допускается, что ряд гидрологических величин
представляет собой одну реализацию СП
Случайный процесс с независимыми сечениями иногда называют
«белым шумом» по аналогии с белым светом

Марковские процессы и цепи Маркова

Случайный процесс
называется марковским, если для любого
момента времени t вероятность каждого из состояний системы в будущем
(при t > t0) зависит только от ее состояния в настоящем (при t = t0) и не
зависит от ее состояния в прошлом (при t < t0)
Марковской цепью или простой марковской цепью называется
марковский процесс с дискретным состоянием и дискретным временем
Марковский СП полностью описывается двумерным законом
распределения. Если Марковский процесс является стационарным и
эргодическим, то его характеристики можно оценить по одной
реализации.
Цепь, в которой условные вероятности состояний в будущем зависят
от ее состояния на нескольких предыдущих шагах, называется сложной
цепью Маркова.

Нормальные (Гауссовские) случайные процессы

Нормальным (гауссовским) случайным процессом X(t) называется
СП, у которого во всех сечениях СВ X(ti) имеет нормальное
распределение
Периодически нестационарные СП
При изучении годовых, месячных, суточных и т.д. процессов, обычно,
наблюдаются внутригодовые и т.д. колебания. В этом случае, в качестве
математической модели можно использовать модель периодически
нестационарного случайного процесса (ПНСП)
Случайный процесс называют периодически нестационарным, если
его вероятностные характеристики инварианты относительно сдвигов на
положительное число Т. Например, при шаге дискретности один месяц
инвариантность должна сохраняться при сдвигах 12, 24, 36 и т.д.

В этой статье Вы найдете всю необходимую информацию, отвечающую на вопрос, как разложить число на простые множители . Сначала дано общее представление о разложении числа на простые множители, приведены примеры разложений. Дальше показана каноническая форма разложения числа на простые множители. После этого дан алгоритм разложения произвольных чисел на простые множители и приведены примеры разложения чисел с использованием этого алгоритма. Также рассмотрены альтернативные способы, позволяющие быстро раскладывать небольшие целые числа на простые множители с использованием признаков делимости и таблицы умножения.

Навигация по странице.

Что значит разложить число на простые множители?

Сначала разберемся с тем, что такое простые множители.

Понятно, раз в этом словосочетании присутствует слово «множители», то имеет место произведение каких-то чисел, а уточняющее слово «простые» означает, что каждый множитель является простым числом . Например, в произведении вида 2·7·7·23 присутствуют четыре простых множителя: 2 , 7 , 7 и 23 .

А что же значит разложить число на простые множители?

Это значит, что данное число нужно представить в виде произведения простых множителей, причем значение этого произведения должно быть равно исходному числу. В качестве примера рассмотрим произведение трех простых чисел 2 , 3 и 5 , оно равно 30 , таким образом, разложение числа 30 на простые множители имеет вид 2·3·5 . Обычно разложение числа на простые множители записывают в виде равенства, в нашем примере оно будет таким: 30=2·3·5 . Отдельно подчеркнем, что простые множители в разложении могут повторяться. Это явно иллюстрирует следующий пример: 144=2·2·2·2·3·3 . А вот представление вида 45=3·15 не является разложением на простые множители, так как число 15 – составное.

Возникает следующий вопрос: «А какие вообще числа можно разложить на простые множители»?

В поисках ответа на него, приведем следующие рассуждения. Простые числа по определению находятся среди , больших единицы. Учитывая этот факт и , можно утверждать, что произведение нескольких простых множителей является целым положительным числом, превосходящим единицу. Поэтому разложение на простые множители имеет место лишь для положительных целых чисел, которые больше 1 .

Но все ли целые числа, превосходящие единицу, раскладываются на простые множители?

Понятно, что простые целые числа разложить на простые множители нет возможности. Это объясняется тем, что простые числа имеют только два положительных делителя – единицу и самого себя, поэтому они не могут быть представлены в виде произведения двух или большего количества простых чисел. Если бы целое число z можно было бы представить в виде произведения простых чисел a и b , то понятие делимости позволило бы сделать вывод, что z делится и на a и на b , что невозможно в силу простоты числа z. Однако считают, что любое простое число само является своим разложением.

А как насчет составных чисел? Раскладываются ли составные числа на простые множители, и все ли составные числа подлежат такому разложению? Утвердительный ответ на ряд этих вопросов дает основная теорема арифметики . Основная теорема арифметики утверждает, что любое целое число a , которое больше 1 , можно разложить на произведение простых множителей p 1 , p 2 , …, p n , при этом разложение имеет вид a=p 1 ·p 2 ·…·p n , причем это разложение единственно, если не учитывать порядок следования множителей

Каноническое разложение числа на простые множители

В разложении числа простые множители могут повторяться. Повторяющиеся простые множители можно записать более компактно, используя . Пусть в разложении числа a простой множитель p 1 встречается s 1 раз, простой множитель p 2 – s 2 раз, и так далее, p n – s n раз. Тогда разложение на простые множители числа a можно записать как a=p 1 s 1 ·p 2 s 2 ·…·p n s n . Такая форма записи представляет собой так называемое каноническое разложение числа на простые множители .

Приведем пример канонического разложения числа на простые множители. Пусть нам известно разложение 609 840=2·2·2·2·3·3·5·7·11·11 , его каноническая форма записи имеет вид 609 840=2 4 ·3 2 ·5·7·11 2 .

Каноническое разложение числа на простые множители позволяет найти все делители числа и число делителей числа .

Алгоритм разложения числа на простые множители

Чтобы успешно справиться с задачей разложения числа на простые множители, нужно очень хорошо владеть информацией статьи простые и составные числа .

Суть процесса разложения целого положительного и превосходящего единицу числа a понятна из доказательства основной теоремы арифметики . Смысл состоит в последовательном нахождении наименьших простых делителей p 1 , p 2 , …,p n чисел a, a 1 , a 2 , …, a n-1 , что позволяет получить ряд равенств a=p 1 ·a 1 , где a 1 =a:p 1 , a=p 1 ·a 1 =p 1 ·p 2 ·a 2 , где a 2 =a 1:p 2 , …, a=p 1 ·p 2 ·…·p n ·a n , где a n =a n-1:p n . Когда получается a n =1 , то равенство a=p 1 ·p 2 ·…·p n даст нам искомое разложение числа a на простые множители. Здесь же следует заметить, что p 1 ≤p 2 ≤p 3 ≤…≤p n .

Осталось разобраться с нахождением наименьших простых делителей на каждом шаге, и мы будем иметь алгоритм разложения числа на простые множители. Находить простые делители нам поможет таблица простых чисел . Покажем, как с ее помощью получить наименьший простой делитель числа z .

Последовательно берем простые числа из таблицы простых чисел (2 , 3 , 5 , 7 , 11 и так далее) и делим на них данное число z . Первое простое число, на которое z разделится нацело, и будет его наименьшим простым делителем. Если число z простое, то его наименьшим простым делителем будет само число z . Здесь же следует напомнить, что если z не является простым числом, то его наименьший простой делитель не превосходит числа , где - из z . Таким образом, если среди простых чисел, не превосходящих , не нашлось ни одного делителя числа z , то можно делать вывод о том, что z – простое число (более подробно об этом написано в разделе теории под заголовком данное число простое или составное).

Для примера покажем, как найти наименьший простой делитель числа 87 . Берем число 2 . Делим 87 на 2 , получаем 87:2=43 (ост. 1) (если необходимо, смотрите статью ). То есть, при делении 87 на 2 получается остаток 1 , поэтому 2 – не является делителем числа 87 . Берем следующее простое число из таблицы простых чисел, это число 3 . Делим 87 на 3 , получаем 87:3=29 . Таким образом, 87 делится на 3 нацело, следовательно, число 3 является наименьшим простым делителем числа 87 .

Заметим, что в общем случае для разложения на простые множители числа a нам потребуется таблица простых чисел до числа, не меньшего, чем . К этой таблице нам придется обращаться на каждом шаге, так что ее нужно иметь под рукой. Например, для разложения на простые множители числа 95 нам будет достаточно таблицы простых чисел до 10 (так как 10 больше, чем ). А для разложения числа 846 653 уже будет нужна таблица простых чисел до 1 000 (так как 1 000 больше, чем ).

Теперь мы обладаем достаточными сведениями, чтобы записать алгоритм разложения числа на простые множители . Алгоритм разложения числа a таков:

Последовательно перебирая числа из таблицы простых чисел, находим наименьший простой делитель p 1 числа a , после чего вычисляем a 1 =a:p 1 . Если a 1 =1 , то число a – простое, и оно само является своим разложением на простые множители. Если же a 1 на равно 1 , то имеем a=p 1 ·a 1 и переходим к следующему шагу.
Находим наименьший простой делитель p 2 числа a 1 , для этого последовательно перебираем числа из таблицы простых чисел, начиная с p 1 , после чего вычисляем a 2 =a 1:p 2 . Если a 2 =1 , то искомое разложение числа a на простые множители имеет вид a=p 1 ·p 2 . Если же a 2 на равно 1 , то имеем a=p 1 ·p 2 ·a 2 и переходим к следующему шагу.
Перебирая числа из таблицы простых чисел, начиная с p 2 , находим наименьший простой делитель p 3 числа a 2 , после чего вычисляем a 3 =a 2:p 3 . Если a 3 =1 , то искомое разложение числа a на простые множители имеет вид a=p 1 ·p 2 ·p 3 . Если же a 3 на равно 1 , то имеем a=p 1 ·p 2 ·p 3 ·a 3 и переходим к следующему шагу.
Находим наименьший простой делитель p n числа a n-1 , перебирая простые числа, начиная с p n-1 , а также a n =a n-1:p n , причем a n получается равно 1 . Этот шаг является последним шагом алгоритма, здесь получаем искомое разложение числа a на простые множители: a=p 1 ·p 2 ·…·p n .

Все результаты, полученные на каждом шаге алгоритма разложения числа на простые множители, для наглядности представляют в виде следующей таблицы, в которой слева от вертикальной черты записывают последовательно в столбик числа a, a 1 , a 2 , …, a n , а справа от черты – соответствующие наименьшие простые делители p 1 , p 2 , …, p n .

Осталось лишь рассмотреть несколько примеров применения полученного алгоритма для разложения чисел на простые множители.

Примеры разложения на простые множители

Сейчас мы подробно разберем примеры разложения чисел на простые множители . При разложении будем применять алгоритм из предыдущего пункта. Начнем с простых случаев, и постепенно их будем усложнять, чтобы столкнуться со всеми возможными нюансами, возникающими при разложении чисел на простые множители.

Пример.

Разложите число 78 на простые множители.

Решение.

Начинаем поиск первого наименьшего простого делителя p 1 числа a=78 . Для этого начинаем последовательно перебирать простые числа из таблицы простых чисел. Берем число 2 и делим на него 78 , получаем 78:2=39 . Число 78 разделилось на 2 без остатка, поэтому p 1 =2 – первый найденный простой делитель числа 78 . В этом случае a 1 =a:p 1 =78:2=39 . Так мы приходим к равенству a=p 1 ·a 1 имеющему вид 78=2·39 . Очевидно, что a 1 =39 отлично от 1 , поэтому переходим ко второму шагу алгоритма.

Теперь ищем наименьший простой делитель p 2 числа a 1 =39 . Начинаем перебор чисел из таблицы простых чисел, начиная с p 1 =2 . Делим 39 на 2 , получаем 39:2=19 (ост. 1) . Так как 39 не делится нацело на 2 , то 2 не является его делителем. Тогда берем следующее число из таблицы простых чисел (число 3 ) и делим на него 39 , получаем 39:3=13 . Следовательно, p 2 =3 – наименьший простой делитель числа 39 , при этом a 2 =a 1:p 2 =39:3=13 . Имеем равенство a=p 1 ·p 2 ·a 2 в виде 78=2·3·13 . Так как a 2 =13 отлично от 1 , то переходим к следующему шагу алгоритма.

Здесь нам нужно отыскать наименьший простой делитель числа a 2 =13 . В поисках наименьшего простого делителя p 3 числа 13 будем последовательно перебирать числа из таблицы простых чисел, начиная с p 2 =3 . Число 13 не делится на 3 , так как 13:3=4 (ост. 1) , также 13 не делится на 5 , 7 и на 11 , так как 13:5=2 (ост. 3) , 13:7=1 (ост. 6) и 13:11=1 (ост. 2) . Следующим простым числом является 13 , и на него 13 делится без остатка, следовательно, наименьший простой делитель p 3 числа 13 есть само число 13 , и a 3 =a 2:p 3 =13:13=1 . Так как a 3 =1 , то этот шаг алгоритма является последним, а искомое разложение числа 78 на простые множители имеет вид 78=2·3·13 (a=p 1 ·p 2 ·p 3 ).

Ответ:

78=2·3·13 .

Пример.

Представьте число 83 006 в виде произведения простых множителей.

Решение.

На первом шаге алгоритма разложения числа на простые множители находим p 1 =2 и a 1 =a:p 1 =83 006:2=41 503 , откуда 83 006=2·41 503 .

На втором шаге выясняем, что 2 , 3 и 5 не являются простыми делителями числа a 1 =41 503 , а число 7 – является, так как 41 503:7=5 929 . Имеем p 2 =7 , a 2 =a 1:p 2 =41 503:7=5 929 . Таким образом, 83 006=2·7·5 929 .

Наименьшим простым делителем числа a 2 =5 929 является число 7 , так как 5 929:7=847 . Таким образом, p 3 =7 , a 3 =a 2:p 3 =5 929:7=847 , откуда 83 006=2·7·7·847 .

Дальше находим, что наименьший простой делитель p 4 числа a 3 =847 равен 7 . Тогда a 4 =a 3:p 4 =847:7=121 , поэтому 83 006=2·7·7·7·121 .

Теперь находим наименьший простой делитель числа a 4 =121 , им является число p 5 =11 (так как 121 делится на 11 и не делится на 7 ). Тогда a 5 =a 4:p 5 =121:11=11 , и 83 006=2·7·7·7·11·11 .

Наконец, наименьший простой делитель числа a 5 =11 – это число p 6 =11 . Тогда a 6 =a 5:p 6 =11:11=1 . Так как a 6 =1 , то этот шаг алгоритма разложения числа на простые множители является последним, и искомое разложение имеет вид 83 006=2·7·7·7·11·11 .

Полученный результат можно записать как каноническое разложение числа на простые множители 83 006=2·7 3 ·11 2 .

Ответ:

83 006=2·7·7·7·11·11=2·7 3 ·11 2 991 – простое число. Действительно, оно не имеет ни одного простого делителя, не превосходящего ( можно грубо оценить как , так как очевидно, что 991<40 2 ), то есть, наименьшим делителем числа 991 является оно само. Тогда p 3 =991 и a 3 =a 2:p 3 =991:991=1 . Следовательно, искомое разложение числа 897 924 289 на простые множители имеет вид 897 924 289=937·967·991 .

Ответ:

897 924 289=937·967·991 .

Использование признаков делимости для разложения на простые множители

В простых случаях разложить число на простые множители можно без использования алгоритма разложения из первого пункта данной статьи. Если числа не большие, то для их разложения на простые множители часто достаточно знать и признаки делимости . Приведем примеры для пояснения.

Например, нам требуется разложить на простые множители число 10 . Из таблицы умножения мы знаем, что 2·5=10 , а числа 2 и 5 очевидно простые, поэтому разложение на простые множители числа 10 имеет вид 10=2·5 .

Еще пример. При помощи таблицы умножения разложим на простые множители число 48 . Мы знаем, что шестью восемь – сорок восемь, то есть, 48=6·8 . Однако, ни 6 , ни 8 не являются простыми числами. Но мы знаем, что дважды три – шесть, и дважды четыре – восемь, то есть, 6=2·3 и 8=2·4 . Тогда 48=6·8=2·3·2·4 . Осталось вспомнить, что дважды два – четыре, тогда получим искомое разложение на простые множители 48=2·3·2·2·2 . Запишем это разложение в канонической форме: 48=2 4 ·3 .

А вот при разложении на простые множители числа 3 400 можно воспользоваться признаками делимости. Признаки делимости на 10, 100 позволяют утверждать, что 3 400 делится на 100 , при этом 3 400=34·100 , а 100 делится на 10 , при этом 100=10·10 , следовательно, 3 400=34·10·10 . А на основании признака делимости на 2 можно утверждать, что каждый из множителей 34 , 10 и 10 делится на 2 , получаем 3 400=34·10·10=2·17·2·5·2·5 . Все множители в полученном разложении являются простыми, поэтому это разложение является искомым. Осталось лишь переставить множители, чтобы они шли в порядке возрастания: 3 400=2·2·2·5·5·17 . Запишем также каноническое разложение данного числа на простые множители: 3 400=2 3 ·5 2 ·17 .

При разложении данного числа на простые множители можно использовать по очереди и признаки делимости и таблицу умножения. Представим число 75 в виде произведения простых множителей. Признак делимости на 5 позволяет нам утверждать, что 75 делится на 5 , при этом получаем, что 75=5·15 . А из таблицы умножения мы знаем, что 15=3·5 , поэтому, 75=5·3·5 . Это и есть искомое разложение числа 75 на простые множители.

Список литературы.

Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
Виноградов И.М. Основы теории чисел.
Михелович Ш.Х. Теория чисел.
Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.

И. В. Яковлев | Материалы по математике | MathUs.ru

Задача С6 на ЕГЭ по математике

1 Необходимая теория
	Числовые множества . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
	Делимость . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
	Чётность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
	Деление с остатком . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
	Каноническое разложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.6 Взаимно простые числа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.7 Последовательности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.8 Арифметическая прогрессия . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

Известно, что на ЕГЭ по математике многие школьники не приступают к задаче С6 и даже не читают её (а зачем? всё равно, мол, не решу). И очень напрасно!

Как правило, задача С6 состоит из двух или трёх пунктов, среди которых есть совсем несложные. За всю задачу даётся 4 первичных балла, по 1-2 балла за каждый пункт. Поэтому, сделав хотя бы часть задачи (скажем, просто предъявив нужный пример в одном из пунктов), можно получить себе в копилку дополнительные первичные баллы. А они дадут прирост итогового результата по стобалльной шкале!

Для решения задачи С6 необходим минимальный запас знаний. Это арифметика 6-го класса (всё, что связано с делимостью) и сведения по прогрессиям из алгебры 9-го класса. Больше ничего.

Почему же задача С6 считается (и, в общем-то, является) самой сложной на ЕГЭ по математике? Она нестандартна. Она требует так называемой математической культуры умения грамотно строить рассуждения. А умение это у подавляющего большинства школьников отсутствует начисто ведь в школе, к сожалению, до развития математической культуры дело обычно не доходит.

Учиться культурно рассуждать можно и обязательно нужно. Задача С6 предоставляет для этого отличную возможность. Получаться начнёт далеко не сразу, так что готовиться к С6 следует начинать задолго до ЕГЭ. Рецепт тут один: решать, решать и решать.

Данное пособие написано с целью помочь школьникам научиться решать нестандартные задачи типа С6. Оно содержит весь нужный теоретический материал и задачи, большая часть которых предлагалась на ЕГЭ и диагностических работах МИОО за последнее время.

Ко всем задачам приведены решения. При этом не ставилась цель сделать решение лаконичным и максимально совершенным технически (в ущерб изложению идей). Ведь учиться математике означает усваивать идеи; на прояснение идей, лежащих в основе решения каждой задачи, и сделан основной упор.

1 Необходимая теория

1.1 Числовые множества

В данном разделе мы определим числовые множества, необходимые для задачи С6. Введённую терминологию нужно твёрдо знать!

Натуральные числа это числа 1; 2; 3; : : : Натуральные числа мы используем для счёта, а счёт начинается с единицы. Поэтому внимание: ноль не является натуральным числом! (Ведь нам вряд ли придёт в голову сказать: ¾На столе стоит ноль чашек¿.)

Множество натуральных чисел обозначается N.

Целые числа это числа 0; 1; 2; 3; : : : Таким образом, целые числа это ноль и ¾плюсминус натуральные¿. Натуральные числа являются целыми положительными числами.

Множество целых чисел обозначается Z. (Именно это обозначение мы постоянно используем в тригонометрических уравнениях для записи ответов.)

Рациональные числа это всевозможные дроби m=n с целыми m и n (при этом, конечно, n 6= 0; чтобы избежать данной оговорки, говорят также, что m целое, а n натуральное).

Любое целое число является в то же время рациональным (например, 3 = 6=2). Однако число 1/2 не является целым.

Множество рациональных чисел обозначается Q.

1.2 Делимость

Понятие делимости относится к целым числам (в частности, к натуральным). Начиная с этого момента все числа считаются целыми. Если в каком-то случае это окажется не так, мы сделаем специальную оговорку.

Целые числа мы обозначаем a; b; c; : : : ; k; l; m; n; : : : ; x; y; z, то есть используем все строчные буквы латинского алфавита.

Вы прекрасно знаете, что число 12 делится на 4, но не делится на 5. Каково формальное определение делимости? Вот оно.

Определение. Число a делится на число b 6= 0, если найдётся число c такое, что a = bc.

Если a делится на b, то число b называется делителем числа a. Например, число 12 имеет шесть делителей: это 1, 2, 3, 4, 6 и 12.

Упражнение. Докажите, что если числа a и b делятся на c, то a + b тоже делится на c.

Сформулируем наиболее важные признаки делимости.

a делится на 2 , последняя цифра a есть 0, 2, 4, 6 или 8;

a делится на 5 , последняя цифра a есть 0 или 5;

a делится на 10 , последняя цифра a равна 0;

a делится на 3 , сумма цифр a делится на 3;

a делится на 9 , сумма цифр a делится на 9.

1.3 Чётность

Соображения, связанные с чётностью или нечётностью, часто фигурируют в задачах С6. Поэтому необходимые факты имеет смысл отметить особо.

Определение. Число называется чётным, если оно делится на 2. Число называется нечётным, если оно не делится на 2.

Вот все чётные числа: 0; 2; 4; 6; : : : Если a чётно, то оно имеет вид a = 2n. А вот все нечётные числа: 1; 3; 5; : : : Ясно, что если a нечётно, то оно имеет вид a = 2n + 1.

Следующие утверждения весьма очевидны, и вы можете использовать их при решении задачи С6 (никто от вас не потребует их доказательства). Но вы можете доказать их в качестве упражнения.

Сумма любого числа чётных слагаемых чётна.

Сумма чётного числа нечётных слагаемых чётна. Сумма нечётного числа нечётных слагаемых нечётна.

Пусть имеется произведение нескольких множителей. Если все множители нечётны, то произведение нечётно. Если хотя бы один множитель чётный, то произведение чётно.

1.4 Деление с остатком

Число 13 не делится на 5. Наибольшее число, которое делится на 5 и не превосходит 13, равно 10 = 5 2. Таким образом, 13 = 5 2+3, и мы скажем, что в результате деления 13 на 5 получается частное 2 и остаток 3.

Оказывается, любое число a можно разделить с остатком на любое число b 6= 0. А именно, найдутся два числа q и r такие, что a = bq + r, и при этом будет выполнено неравенство 0 6 r < jbj. Число q назвается частным, а число r остатком от деления a на b.

Если r = 0, то есть a = bq, то a делится на b.

Упражнение. Найдите частное и остаток от деления: а) 7 на 2; б) 15 на 4; в) 2012 на 5; г) 1001 на 13; д) 9 на 8; е) 8 на 9.

Остаток от деления любого нечётного числа на 2 равен единице. Вот почему всякое нечётное число может быть записано в виде 2n + 1.

Остатки оказываются полезными во многих ситуациях. Допустим, в ходе решения задачи вам нужно доказать, что равенство n2 = 3k + 2 не может выполняться ни при каких целых числах n и k. Рассуждаем следующим образом.

Число n при делении на 3 может давать остатки 0, 1 или 2. Иными словами, возможны три случая: n = 3m, n = 3m + 1 или n = 3m + 2. Какие остатки при делении на 3 будут у числа n2 ? Давайте посмотрим, что получается в каждом из трёх случаев.

(3m)2 = 9m2 (остаток 0);

(3m + 1)2 = 9m2 + 6m + 1 (остаток 1);

(3m + 2)2 = 9m2 + 12m + 4 = (9m2 + 12m + 3) + 1 (остаток 1):

Таким образом, квадрат целого числа при делении на 3 не может давать остаток 2. Следовательно, равенство n2 = 3k + 2 действительно невозможно ни при каких n и k.

Упражнение. Докажите, что число 100: : : 004 (между 1 и 4 стоит любое число нулей) не является квадратом целого числа.

Упражнение. Докажите, что квадрат целого числа при делении на 4 может давать только два остатка: 0 и 1.

Упражнение. Докажите, что n3 + 2n делится на 3.

1.5 Каноническое разложение

Всякое число делится на 1 и на само себя. Если натуральное число p не равно 1 и не имеет других натуральных делителей, кроме 1 и p, то такое число p называется простым.

Вот первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19. Число 2 единственное чётное простое число.

Число, не равное 1 и не являющееся простым, называется составным. Например, 15 составное число (оно делится на 3). Число 1036 тоже составное (оно чётное). Единица не является ни простым числом, ни составным.

Упражнение. Число 315 1 является составным. Почему?

Оказывается, всякое число можно разложить на простые множители. Например:

30 = 2 3 5; 504 = 2 2 2 3 3 7 = 23 32 7:

Такое разложение единственно с точностью до порядка множителей и называется каноническим разложением. Утверждение о существовании и единственности канонического разложения носит название основной теоремы арифметики.

Каноническое разложение даёт полную картину делителей данного числа (и, в частности, позволяет найти их количество). Именно, пусть a = pn 1 1 pn 2 2 : : : pn s s каноническое разложение числа a. Тогда каноническое разложение любого делителя числа a состоит из простых множителей, входящих в набор fp1 ; p2 ; : : : ; ps g, показатели степени которых не превосходят соответственно чисел n1 ; n2 ; : : : ; ns . Например, любой делитель числа 504 = 23 32 7 имеет вид 2a 3b 7c , где a 2 f0; 1; 2; 3g, b 2 f0; 1; 2g и c 2 f0; 1g.

Упражнение. Пусть p простое число. Сколько делителей у числа: а) p2 ; б) p3 ; в) pn ?

Упражнение. Пусть p и q простые числа. Сколько делителей у числа: а) pq; б) p2 q3 ; в) pm qn ?

Упражнение. Обобщив рассуждения пункта в) предыдущего упражнения, покажите, что количество делителей числа a = pn 1 1 pn 2 2 : : : pn s s равно (n1 + 1)(n2 + 1) : : : (ns + 1). Найдите, сколько делителей имеет число 504.

Упражнение. Найдите канонические разложения чисел 540 и 252. С помощью полученных разложений найдите НОД (540; 252) наибольший общий делитель этих чисел.

1.6 Взаимно простые числа

Числа называются взаимно простыми, если они не имеют общих делителей кроме 1. Иными словами, числа a и b взаимно просты, если НОД (a; b) = 1. Можно сказать и так: числа a и b взаимно просты тогда и только тогда, когда дробь a=b несократима.

Например, числа 8 и 15 взаимно просты. Числа 9 и 15 не являются взаимно простыми у них имеется общий делитель 3.

Числа взаимно просты тогда и только тогда, когда их канонические разложения состоят из непересекающихся наборов простых чисел. Например, числа 23 5 132 и 32 73 11 являются взаимно простыми.

Свойства взаимно простых чисел. Пусть числа a и b взаимно просты. Тогда справедливы следующие утверждения.

1. Если некоторое число делится на a и b, то оно делится и на их произведение ab.

2. Если an делится на b, то n делится на b.

(Вы легко поймёте, почему так получается, если представите себе ¾непересекающиеся¿ канонические разложения чисел a и b и вдобавок вспомните, что каноническое разложение делителя служит ¾частью¿ канонического разложение делимого числа.)

Согласно утверждению 1, например, если некоторое число делится на 8 и на 15, то оно делится на 8 15 = 120. То, что числа взаимно просты, важное условие. Так, 12 делится на 4 и на 6, но не делится на 4 6 = 24.

Упражнение. Какие цифры можно вставить вместо звёздочек в записи 35 4 , чтобы полученное пятизначное число делилось на 45?

Утверждение 2 обычно работает в ситуациях типа следующей. Пусть, например, 5n = 9m. Так как 5n делится на 9 и числа 5 и 9 взаимно просты, то n делится на 9. По той же самой причине m делится на 5.

1.7 Последовательности

Что такое последовательность? Представьте себе устройство, которое с некоторыми интервалами выдаёт одно число за другим. Например: 2, 3, 15, 28, 6, 0, 3, . . . Набор чисел на выходе этого устройства и будет последовательностью.

Более строго, последовательность чисел, или числовая последовательность это набор чисел, в котором каждому числу можно присвоить некоторый номер, причём каждому номеру отвечает единственное число данного набора. Номер это натуральное число; нумерация начинается с единицы.

Так, в приведённой выше последовательности первый номер имеет число 2 (это первый член последовательности), а номер пять число 6 (это пятый член последовательности).

Число с номером n (то есть n-й член последовательности) обозначается an (или bn , cn , . . .). Весьма удобно, когда n-й член последовательности можно задать некоторой формулой. Например, формула an = 2n 3 задаёт последовательность: 1; 1; 3; 5; 7; : : : Формула an = (1)n

задаёт последовательность: 1; 1; 1; 1; : : :

Упражнение. Придумайте формулу n-го члена для следующих последовательностей: а) 1; 3; 5; 7; : : : ; б) 5; 8; 11; 14; : : : ; в) 1; 4; 9; 16; : : : ; г) 1; 2; 3; 4; : : :

Все рассмотренные нами последовательности являются бесконечными, то есть содержащими бесконечное множество чисел. Но бывают и конечные последовательности. Собственно, любой конечный набор чисел является конечной последовательностью. Например, конечная последовательность 1; 2; 3; 4; 5 состоит из пяти чисел.

В задаче С6 нужны два специальных вида последовательностей: арифметическая и геометрическая прогрессии.

1.8 Арифметическая прогрессия

Арифметическая прогрессия это последовательность, каждый член которой (начиная со второго) равен сумме предыдущего члена и некоторого фиксированного числа:

an+1 = an + d (n = 1; 2; : : :):

Фиксированное число d называется разностью арифметической прогрессии.

Например, последовательность 2; 5; 8; 11; : : : является арифметической прогрессией с первым членом 2 и разностью 3.

Случайная величина Vназываетсяцентрированной , если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величиныVна неслучайную функцию φ(t):X(t)=Vφ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:

Выражение вида
, где φ k ( t ), k =1;2;…-неслучайные функции; , k =1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X ( t ), при этом случайные величины называются коэффициентами канонического разложения; а неслучайные функции φ k ( t ) - координатными функциями канонического разложения.

Рассмотрим характеристики случайного процесса

Так как по условию
то

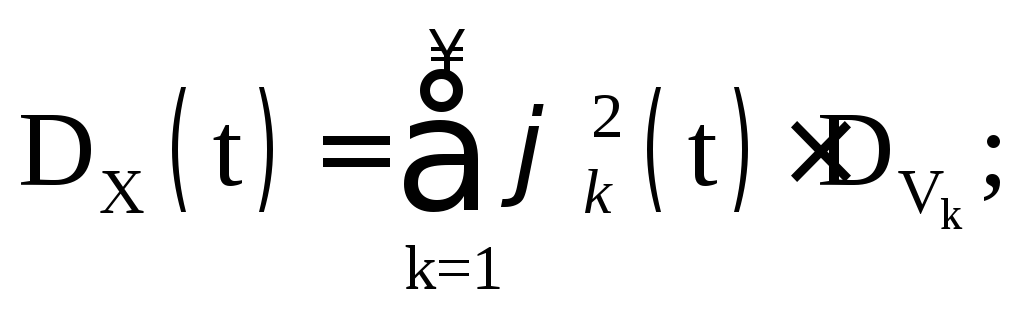
Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин V к. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции:
. После разложения
в двойной ряд Фурье по координатным функциям φ к (t):

получают значения дисперсий
случайных величинV k .

4.2. Понятие обобщенной функции. Дельта-функция Дирака. Интегральное каноническое представление случайных процессов.

Обобщенной функцией называется предел последовательности однопараметрического семейства непрерывных функций.

Дельта-функция Дирака
- это обобщенная функция, являющаяся результатом предельного перехода при
в семействе функций

Среди свойств -функции отметим следующее:

3. Если f(t)- непрерывная функция, то

Случайный процесс Х( t ), корреляционная функция которого имеет вид называется нестационарным «белым шумом». Если W ( t 1 )= W - const , то Х( t )-стационарный «белый шум».

Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называетсяинтенсивностью «белого шума».

Интегральным каноническим представлением случайного процесса Х( t ) называется выражение вида
где
- случайная центрированная функция;
- неслучайная функция непрерывных аргументов

Корреляционная функция такого случайного процесса имеет вид:

Можно показать, что существует неслучайная функция G(λ) такая, что

где G(λ 1) - плотность дисперсии; δ(х) - дельта-функция Дирака. Получаем

Следовательно, дисперсия случайного процесса Х(t):

4.3. Линейные и нелинейные преобразования случайных процессов

Рассматривается следующая задача: на вход системы (устройства, преобразователя) Sподается «входной сигнал», имеющий характер случайного процесса Х(t). Система преобразовывает его в «выходной сигнал»Y(t):

Формально преобразование случайного процесса Х(t) вY(t) может быть описано с помощью так называемого оператора системы А t:

Y(t)=A t (Х(t)).

Индекс tпоказывает, что данный оператор осуществляет преобразование по времени. Возможны следующие постановки задачи о преобразовании случайного процесса.

Известны законы распределения или общие характеристики случайного процесса Х(t) на входе в системуS, задан оператор А t системыS, требуется определить закон распределения или общие характеристики случайного процессаY(t) на выходе системыS.

Известны законы распределения (общие характеристики) случайного процесса Х(t) и требования к случайному процессуY(t); надо определить вид оператора А t системыS, наилучшим образом удовлетворяющего заданным требованиям кY(t).

Известны законы распределения (общие характеристики) случайного процесса Y(t) и задан оператор А t системыS; требуется определить законы распределения или общие характеристики случайного процесса Х(t).

Принята следующая классификация операторов А t системыS:

Операторы системы

Линейные LНелинейныеN

Линейные однородные L 0 Линейные неоднородныеL н

Рассмотрим воздействие линейной неоднородной системы

L н (...)=L 0 (…)+φ(t)

на случайный процесс Х(t), имеющий следующее каноническое разложение:

Получаем:

введем обозначения

тогда каноническое разложение Y(t) приобретает вид:

Математическое ожидание случайного процессаY(t):

корреляционная функция случайного процесса Y(t):

следовательно,

С другой стороны

Дисперсия случайного процесса Y(t):

В заключении этого пункта отметим, что операторы дифференцирования и интегрирования случайных процессов являются линейными однородными.

2. Рассматривается квадратичное преобразование:

Y(t)=(X(t)) 2 ,

V k -центрированные случайные величины, имеющие симметричное относительно нуля распределение; любые четыре из них независимы в совокупности. Тогда

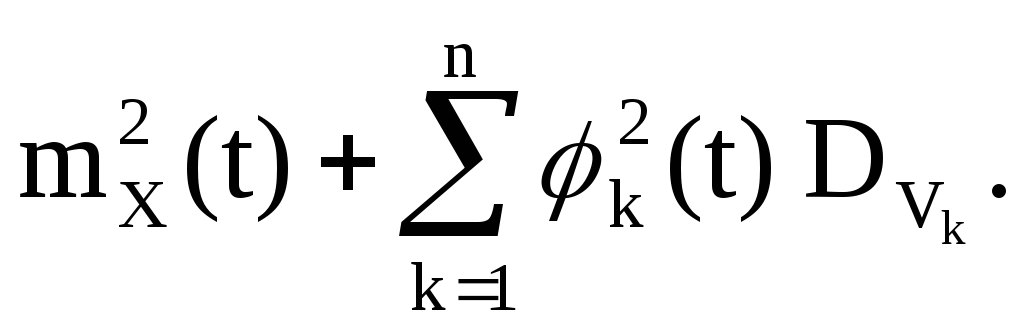
Введем неслучайные функции

и случайные величины

тогда случайный процесс Y(t) приобретает вид

Получено каноническое разложение случайного процесса Y(t). Корреляционная функцияY(t):

Формулировка. Дано натуральное число n (n > 1) . Получить его каноническое разложение на простые сомножители, то есть представить в виде произведения простых сомножителей. При этом в разложении допустимо указывать множитель 1. Например, 264 = 2 * 2 * 2 * 3 * 11 (программе допустимо выдать ответ 264 = 1 * 2 * 2 * 2 * 3 * 11).

Решение. Данная задача имеет достаточно красивое решение.

Из основной теоремы арифметики известно, что для любого натурального числа больше 1 существует его каноническое разложение на простые сомножители, причем это разложение единственно с точностью до порядка следования множителей. То есть, например, 12 = 2 * 2 * 2 и 12 = 3 * 2 * 2 – это одинаковые разложения.

Рассмотрим каноническую форму любого числа на конкретном примере. Например, 264 = 2 * 2 * 2 * 3 * 11. Каким образом можно выявить эту структуру? Чтобы ответить на этот вопрос, вспомним изложенные в любом школьном курсе алгебры правила деления одночленов, представив, что числа в каноническом разложении являются переменными. Как известно, если разделить выражение на переменную в некоторой степени, содержащуюся в этом выражении в той же степени, оно вычеркивается в ее записи.

То есть, если мы разделим 264 на 2, то в его каноническом разложении уйдет одна двойка. Затем мы можем проверить, делится ли снова получившееся частное на 2. Ответ будет положительным, но третий раз деление даст остаток. Тогда нужно брать для рассмотрения следующее натуральное число 3 – на него частное разделится один раз. В итоге, проходя числовую прямую в положительном направлении, мы дойдем до числа 11, и после деления на 11 n станет равно 1, что будет говорить о необходимости закончить процедуру.

Почему при таком «вычеркивании» найденных сомножителей мы не получим делимостей на составные числа? На самом деле, здесь все просто – любое составное число является произведением простых сомножителей, меньших его. В итоге получается, что мы вычеркнем из n все сомножители любого составного числа, пока дойдем до него самого в цепочке делений. Например, при таком переборе n никогда не разделится на 4, так как «по пути» к этому числу мы вычеркнем из n все сомножители-двойки.

Алгоритм на естественном языке:

1) Ввод n ;

2) Присвоение переменной p числа 2;

3) Вывод числа n , знака равенства и единицы для оформления разложения;

4) Запуск цикла с предусловием n < > 1 . В цикле: