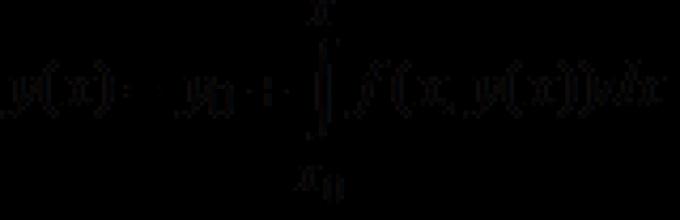Рассмотрим задачу Коши (5.2), (5.6) для дифференциального уравнения первого порядка: найти решение уравнения y"=f(x,y), удовлетворяющее условию y(x 0)=y 0 . Пусть y(x)- решение поставленной задачи Коши. Подставив это решение в уравнение (5.2), получим тождество y"(x) ≡ f(x,y(x)). Интегрируя это тождество по x, получаем

или, что тоже самое,

. (5.15)

Таким образом, мы показали, что всякое решение задачи Коши (5.2), (5.6) есть решение интегрального уравнения (5.15). С другой стороны, если y(x)- решение интегрального уравнения (5.15), то дифференцируя (5.15) по x, получаем, что y(x)- решение задачи Коши (5.2), (5.6).

Решение интегрального уравнения (5.15) будем искать с помощью метода последовательных приближений. Положим

y 0 (x)=y 0 , . (5.16)

Если оператор

- (5.17)

сжимающий , то последовательные приближения (5.16) сходятся к решению интегрального уравнения (5.15), а, следовательно и дифференциального уравнения y" = f(x,y), удовлетворяющего условию y(x 0) = y 0 . Желающие могут познакомиться с доказательством сжимаемости оператора (5.17) в .

Пример №1 . Найдём с помощью метода последовательных приближений решение уравнения y" = y, удовлетворяющее условию y(0)=1. Подставляя y(0)=1 в (5.16), получаем

y 0 =1, …,

С другой стороны, решая исходную задачу Коши, имеем y = e x .

Таким образом, нами получено разложение функции e x в ряд Тейлора в нуле (ряд Маклорена).

Перейдём теперь к изложению численного метода Эйлера решения задачи Коши (5.2), (5.6). Разобьём отрезок , на котором мы ищем решение, на части точками x 0 = a то заменяя производную y"(x i) конечной разностью в уравнении (5.2), получаем , или, что то же самое,

y i +1 = y i + h·f(x i , y i), (5.17)

Соотношение (5.17) является расчётной формулой метода Эйлера численного решения задачи Коши (5.2), (5.6). Вычислив y i , i = 0,1,..,n получим таблицу значений решения в точках x i , i = 0,1,..,n Для оценки погрешности на одном шаге сетки в методе Эйлера разложим точное решение y(x) по формуле Тейлора в окрестности точки xi до членов второго порядка малости

y(x i +1)=y(x i +h)=y(x i)+y"(x i)h+o(h 2)=y i +hf(x i ,y i)+o(h 2).

Сравнивая с (5.17) видим, что погрешность формулы (5.17) равна o(h 2). К сожалению, метод Эйлера накапливает ошибку от шага к шагу. Поэтому на практике пользуются либо модификациями метода Эйлера, например методом прогноза и коррекции , либо другими методами, в частности методом Рунге-Кутта .

Класс уравнений, для которых можно получить точное решение, то есть, аналитическую функцию, удовлетворяющую заданному дифференциальному уравнению и всем дополнительным условиям (задача Коши), очень узок. Чаще всего дифференциальные уравнения решаются приближенно. С одним из методов – итерационным – мы познакомились при доказательстве теоремы существования и единственности.

1. Приближение решения с помощью степенного ряда . Представим, что мы должны решить задачу Коши для дифференциального уравнения -го порядка с начальным условием . Если функция в правой части уравнения разлагается в ряды по всем своим переменным, удобно искать решение дифференциального уравнения в окрестности точки в виде ряда Тейлора по степеням . Представим решение в виде . Из начальных условий и свойств коэффициентов ряда Тейлора следует, что все коэффициенты разложения вплоть до нам известны:

остальные – неизвестные – коэффициенты обозначаются буквами и определяются сравнением коэффициентов при одинаковых степенях, находящихся в обеих частях дифференциального уравнения.

П р и м е р. Решить следующую задачу Коши: , .

Искать решение будем в виде ряда по степеням . В соответствии с начальными условиями . Подставим хотя бы первые слагаемые рядов в уравнение:

Перемножим входящие в правую часть сомножители:

А теперь сравним свободные члены (они равны) и коэффициенты при , при и при : . Отсюда .

Мы могли бы и далее сравнивать коэффициенты при степенях в уравнении и получать значения других коэффициентов . Тем более применение программ MAXIMA упрощает этот процесс. В данном случае мы получили решение в виде ряда, первые члены которого известны: .

Задачу Коши для системы уравнений можно решать подобным способом.

2. Метод Эйлера и его модификации . Познакомимся с методом Эйлера численного решения задачи Коши для дифференциального уравнения первого порядка . Предположим, что мы должны решить задачу на отрезке . Разделим отрезок на равных частей, равных . Заменим на каждом отрезке , , решение дифференциального уравнения линейной функцией . При этом имеем узловые значения решения:

Мы здесь приравниваем отношение приращений функции и аргумента производной в точке, соответствующей началу отрезка разбиения:

.

Очевидно, что такое приближение является тем менее точным, чем дальше мы отойдем от точки . Метод Эйлера является наиболее примитивным. Здесь интегральная кривая заменяется ломаной, состоящей из прямолинейных отрезков. Возможны его некоторые модификации, несколько улучшающие точность. Например, если брать постоянные значения в виде

Наиболее распространенным численным методом решения указанной задачи Коши является метод Рунге-Кутта. При решениидифференциального уравнения этим методом интегральная кривая заменяется ломаной, состоящей из кусков парабол. Метод Рунге-Кутта встроен в пакет программ MAXIMA.

Например, мы хотим решить дифференциальное уравнение с начальным условием . При этом мы задаем отрезок , на котором хотим получить численное решение и шаг разбиения этого отрезка, равный 0.05. Мы должны ввести команду

load(dynamics); rk(y^2+x,y,0.3,);

После того, как мы нажмем клавиши Shift+Enter, получим данные

[,,,,,,,,,,,,,,,,,,,,].

Это означает, что мы получили узловые значения решения: y (0.05)= 0.30583128660202,…, y (0.4)= 0.42905553899765,…..

Приближенное решение дифференциальных уравнений высших порядков сводятся к решению систем уравнений первого порядка. Например, требуется решить дифференциальное уравнение на отрезке с шагом 0.1 при начальных условиях . Введем новую функцию . Теперь уравнение запишется в виде системы

с начальными условиями .

Для получения решения методом Рунге-Кутта вводим команду load(dynamics); rk(, , , ).

Мы получим значения в узлах:

[,,,,,,,,,,,,,,,,[

1.6,0.55276102463945,-9.157645341403534],,

Это означает, что, например, y(0.5)= 1.227625229955781,

z(0.5)= 0.80905909503231.

3. Графический метод . Этим методом можно решать дифференциальные уравнения первого порядка вида . Если нам необходимо построить интегральные кривые, которые являются графиками решений приведенного уравнения, в какой-то части плоскости , мы каждой точке этой области ставим в соответствие значение , которое совпадает с тангенсом угла наклона касательной к интегральной кривой, проходящей через точку . Зная точку и направление движения по кривой из этой точки, мы переходим к близкой точке, в которой также определяем направление движения,…. Так, двигаясь от точки к точке, мы построим соответствующую интегральную кривую, то есть, решим задачу Коши .

Реальное построение решения таким методом было бы очень сложным без применения компьютерной техники. MAXIMA содержит программу построения графических решений. Если мы введем load(plotdf); plotdf(f(x,y),,) , на экране появится прямоугольник , в точках которого указаны направления касательных к интегральным кривым, проходящим через эти точки. Если щелкнуть курсором по выбранной точке на плоскости, компьютер нарисует интегральную кривую, проходящую через соответствующую точку.

Например, мы хотим построить интегральную кривую уравнения , расположенную в прямоугольнике и проходящую через точку (11,2) .

Введем load(plotdf); plotdf((5-x^2)/(2*x*y-y^2),,); и нажмем Shift+Enter. Мы получим выбранный прямоугольник с указанием направлений из точек прямоугольника. Теперь щелкнем по точке (11,2) , и нарисуется соответствующая интегральная кривая.

Как найти частное решение ДУ приближённо с помощью ряда?

Продолжая изучать практические приложения теории рядов, рассмотрим ещё одну распространённую задачу, название которой вы видите в заголовке. И, чтобы не чувствовать себя газонокосилкой на протяжении урока, давайте сразу же разберёмся в сути задания. Три вопроса и три ответа:

Что нужно найти? Частное решение дифференциального уравнения . Намёк между строк шепчет, что к данному моменту желательно хотя бы понимать, что такое дифференциальное уравнение и что такое его решение.

КАК по условию требуется это решение? Приближённо – с помощью ряда .

И третий закономерный вопрос: почему приближённо? Этот вопрос я уже освещал на уроке Методы Эйлера и Рунге-Кутты , однако повторение не помешает. Будучи сторонником конкретики, вернусь к простейшему дифференциальному уравнению . В ходе первой лекции по диффурам мы нашли его общее решение (множество экспонент) и частное решение , соответствующее начальному условию . График функции – это самая обычная линия, которую нетрудно изобразить на чертеже.

Но то элементарный случай. На практике встречается великое множество дифференциальных уравнений, неразрешимых аналитически точно (по крайне мере, известными на сегодняшний день способами). Иными словами, как ни крути такое уравнение – проинтегрировать его не удастся. А закавыка состоит в том, что общее решение (семейство линий на плоскости) может существовать . И тогда на помощь приходят методы вычислительной математики.

Встречаем нашу радость!

Типовая задача формулируется следующим образом:

… , удовлетворяющее начальному условию , в виде трёх (реже – четырёх-пяти) отличных от нуля членов ряда Тейлора .

Искомое частное решение раскладывается в данный ряд по известной формуле:

Единственное, здесь вместо буквы «эф» используется «игрек» (так уж повелось).

Идея и смысл тоже знакомы : для некоторых диффуров и при некоторых условиях (не будем вдаваться в теорию) построенный степенной ряд будет сходиться к искомому частному решению . То есть, чем больше членов ряда мы рассмотрим, тем точнее график соответствующего многочлена приблизит график функции .

Следует отметить, что вышесказанное применимо и к самым простым случаям. Проведём незамысловатое детское исследование на том же горшке:

Пример 1

Найти приближённо частное решение дифференциального уравнения , удовлетворяющее начальному условию в виде четырёх первых отличных от нуля членовряда Тейлора.

Решение : в условиях данной задачи , поэтому общая формула Тейлора трансформируется в частный случай разложения в ряд Маклорена :

Немного забегая вперёд, скажу, что в практических заданиях значительно чаще встречается именно этот, более компактный ряд.

Занесите обе рабочие формулы в свой справочник.

Разбираемся со значениями . Этапы решения удобно занумеровать:

0) На нулевом шаге записываем значение , которое всегда известно из условия. В тетради итоговые результаты пунктов желательно обводить в кружок, чтобы они были хорошо видны и не затерялись в решении. Мне по техническим причинам сподручнее выделять их жирным шрифтом. Кроме того, отмечаем, что данное значение не равно нулю ! Ведь по условию требуется найти четыре отличных от нуля членовряда.

1) Вычислим . Для этого в правую часть исходного уравнения вместо «игрека» подставляем известное значение :

2) Вычислим . Сначала находим вторую производную :

Подставляем в правую часть найдённое в предыдущем пункте значение :

В распоряжении уже три ненулевых члена разложения, нужен ещё один:

Пример 2

Найти приближённо частное решение дифференциального уравнения , удовлетворяющее начальному условию в виде трёх первых отличных от нуля членовряда Тейлора.

Решение начинается стандартной фразой:

В данной задаче , следовательно:

Теперь последовательно находим значения – до тех пор, пока не будут получены три ненулевых результата. Если повезёт, то отличны от нуля будут – это идеальный случай с минимальным количеством работы.

Нарезаем пункты решения:

0) По условию . Вот и первый успех.

1) Вычислим . Сначала разрешим исходное уравнение относительно первой производной, то есть, выразим . Подставим в правую часть известные значения :

Получена баранка и это не есть хорошо, поскольку нас интересуют ненулевые значения. Однако ноль – тоже результат , который не забываем обвести в кружок или выделить каким-нибудь другим способом.

2) Находим вторую производную и подставляем в правую часть известные значения :

Второй «не ноль».

3) Находим – производную от второй производной:

Вообще, задание чем-то напоминает Сказку про Репку, когда дедка, бабка и внучка зовут на помощь жучку, кошку и т.д. И в самом деле, каждая следующая производная выражается через своих «предшественников».

Подставим в правую часть известные значения :

Третье ненулевое значение. Вытащили Репку.

Аккуратно и внимательно подставляем «жирные» числа в нашу формулу:

Ответ : искомое приближенное разложение частного решения:

В рассмотренном примере попался всего один ноль на втором месте, и это не так уж плохо. В общем случае нулей может встретиться сколько угодно и где угодно. Повторюсь, их очень важно выделять наряду с ненулевыми результатами, чтобы не запутаться в подстановках на завершающем этапе.

Вот, пожалуйста – бублик на самом первом месте:

Пример 3

Найти приближённо частное решение дифференциального уравнения , соответствующее начальному условию , в виде трёх первых отличных от нуля членовряда Тейлора.

Примерный образец оформления задачи в конце урока. Пункты алгоритма можно и не нумеровать (оставляя, например, пустые строки между шагами), но начинающим рекомендую придерживаться строгого шаблона.

Рассматриваемая задача требует повышенного внимания – если допустить ошибку на каком-либо шаге, то всё остальное тоже будет неверным! Поэтому ваша ясная голова должна работать как часы. Увы, это не интегралы или диффуры , которые надёжно решаются и в утомлённом состоянии, поскольку позволяют выполнить эффективную проверку.

На практике заметно чаще встречается разложение в ряд Маклорена :

Пример 4

Решение : в принципе, можно сразу записать разложение Маклорена , но оформление задачи академичнее начать с общего случая:

Разложение частного решения дифференциального уравнения при начальном условии имеет вид:

В данном случае , следовательно:

0) По условию .

Ну что поделать…. Будем надеяться, что нулей встретится поменьше.

1) Вычислим . Первая производная уже готова к употреблению. Подставим значения :

2) Найдём вторую производную:

И подставим в неё :

Резво дело пошло!

3) Находим . Распишу очень подробно:

Заметьте, что к производным применимы обычные алгебраические правила: приведение подобных слагаемых на последнем шаге и запись произведения в виде степени: (там же).

Подставим в всё, что нажито непосильным трудом :

Три ненулевых значения рождены.

Подставляем «жирные» числа в формулу Маклорена, получая тем самым приближенное разложение частного решения:

Ответ :

Для самостоятельного решения:

Пример 5

Представить приближенно частное решение ДУ, соответствующее заданному начальному условию , в виде суммы трех первых отличных от нуля членов степенного ряда.

Примерный образец оформления в конце урока.

Как видите, задача с частным разложением в ряд Маклорена оказалась даже труднее общего случая. Сложность рассматриваемого задания, как мы только что убедились, состоит не столько в самом разложении, сколько в трудностях дифференцирования. Более того, порой, приходится находить 5-6 производных (а то и больше), что повышает риск ошибки. И в завершении урока предлагаю пару задач повышенной сложности:

Пример 6

Решить дифференциальное уравнение приближённо с помощью разложения частного решения в ряд Маклорена, ограничившись тремя первыми ненулевыми членами ряда

Решение :перед нами диффур второго порядка, но это практически не меняет дела. По условию и нам сразу же предложено воспользоваться рядом Маклорена, чем мы не преминем воспользоваться. Запишем знакомое разложение, прихватив на всякий пожарный побольше слагаемых:

Алгоритм работает точно так же:

0) – по условию.

1) – по условию.

2) Разрешим исходное уравнение относительно второй производной: .

И подставим :

Первое ненулевое значение

Щёлкаем производные и выполняем подстановки:

Подставим и :

Подставим :

Второе ненулевое значение.

5) – по ходу дела приводим подобные производные.

Подставим :

Подставим :

Наконец-то. Впрочем, бывает и хуже.

Таким образом, приближенное разложение искомого частного решения:

Обыкновенными дифференциальными уравнениями называются такие уравнения, которые содержат одну или несколько производных от искомой функции y=y(x)

F(x,y,y 1 ,…,y (n)) = 0, где x-независимая переменная.

Решением дифференциального уравнения называется функция , которая после её подстановки в уравнение превращает его в торжество.

Некоторые методы решения известны по курсу дифференциальных уравнений. Для ряда уравнений первого порядка (с разделяющимися переменных однородных, линейных и др) удается получить решение в виде формул путем аналитических преобразований.

В большинстве случаев для решения дифференциальных уравнений используются приближенные методы, которые можно разделить на две группы:

1)аналитические методы, дающие решение в виде аналитического выражения;

2)численные методы, дающие приближенное решение в виде таблицы.

Рассмотрим перечисленные методы в виде следующих примеров.

8.1 Метод последовательного дифференцирования.

Рассмотрим уравнение:

с начальными условиями , где – заданные числа.

Предположим, что искомое решение y=f(x) может быть решено в ряд Тейлора по степеням разности (x-x 0):

2 n +….

Начальные условия (8.2) дают нам значения y (k) (x 0) при k=0,1,2,...,(n-1). Значения y (n) (x 0) найдем из уравнения (8.1), подставляя (x-x 0) и используя начальные условия (8.2):

y (n) (x 0) = f(x 0 ,y 0 ,y " 0 ,...,y 0 (n-1))

Значения y (n+1) (x 0), y (n+2) (x 0)... последовательно определяются дифференцированием уравнение (8.1) и подстановкой x=x 0 , y (k) (x 0)=y 0k (k – 0,1,2).

ПРИМЕР: Найти первые семь членов разложения в степенной ряд решения y=y(x) уравнения y "" +0,1(y ") 2 +(1+0,1x)y=0 с начальными условиями y(0)=1; y " (0)=2.

РЕШЕНИЕ: Решение уравнения ищем в виде ряда:

y(x)=y(0)+y"(0)x/1!+y""(0)x 2 /2!+...+y (n) (0)x n /n!...

Из начальных условий имеем y(0)=1, y " (0)=2. Для определения y "" (0) разрешим данное уравнение относительно y"":

y""(0)= – 0,1(y ") 2 – (1+0,1x)y (8.3)

Используя начальные условия, получим

y""(0)= –0,1*4 – 1*1= –1,4

Дифференцируя по x левую и правую части уравнения (8.3)

y"""= – 0,2y"y"" – 0,1(xy"+y) – y",

y (4) = – 0,2(y"y"""+y"" 2) – 0,1(xy""+2y") – y"",

y (5) = – 0,2(y"y (4) +3y""y""") – 0,1(xy"""+3y"") – y""",

y (6) = – 0,2(y"y (5) +4y""y (4) +3y""" 2) – 0,1(xy (4) +4y""" – y (4))

Подставляя начальные условия и значение y""(0), находим y"""(0)= – 1,54;

y (4) (0)= – 1,224; y (5) (0)=0,1768; y (6) (0)= – 0,7308. Таким образом, искомое приближенное решение запишется в виде: y(x) ≈ 1 + 2x – 0,7x 2 – 0,2567x 3 + 0,051x 4 + 0,00147x 5 – 0,00101x 6 .

8.2 Метод эйлера

Простейшими из численных методов решения дифференциальных уравнений является метод Эйлера, который основан на замене искомой функции многочленом первой степени, т.е. линейной экстраполяцией. Речь идет о нахождении значений функции в соседних точках аргумента x не между ними.

Выберем шаг h малым, чтобы для всех x между x 0 и x 1 =x 0 +h значение функции y мало отличалось от линейной функции. Тогда на указанном интервале y = y 0 + (x – x 0)y" = y 0 + (x –

Продолжая таким же способом определять значения функции, убеждаемся, что метод Эйлера представляется в виде последовательного выполнения формул:

∆y k = y" k h

y k+1 = y k + ∆y k

ПРИМЕР

Решим методом Эйлера уравнения y" = x – y с начальным условием х 0 =0, у 0 =0 на отрезке с шагом h=0,1.

Вычисления приведены в таблице.

Первая строка в столбцах 1 и 2 заполнена по начальным данным. Затем вычисляется у" по заданному уравнению (в столбце 4), затем ∆y = y"h – в столбце (4).

Столбец (5) содержит таблицу значений точного решения заданного уравнения.

Из таблицы видно что при х=1 относительная ошибка метода Эйлера составляет δ=0,37 - 0,35/0,37*100%≈5,4%

УТОЧНЕННЫЙ МЕТОД ЭЙЛЕРА

При том же объеме вычислительной работы дает более высокую точность.

Ранее мы считали подынтегральную функцию постоянной, равной её значению f(x k ,y k) на левом конце участка. Более точное значение получится если полагать f(x,y(x)) равной значению в центре участка. Для этого надо брать двойной участок (x k-1 ,x k+1), заменив формулу

y k+1 =y k +∆y k на y k+1 =y k-1 +2hy" k (8.5)

Эта формула и выражает уточненный метод Эйлера. Но в этом случае надо придерживать следующей последовательности действий:

ПРИМЕР Для сравнения рассмотрим то же уравнение y" = x – y с начальными условиями x 0 =0, y 0 =0. Уточненный метод, как видно из таблицы дает более высокую точность относительная погрешность при х=1, у=0,370, а у точн 0,368.

С дифференциальными уравнениями в частных производных и интегральными уравнениями приходится встречаться в самых разнообразных областях естествознания, причем получить их решение в явном виде, в виде конечной формулы, удается только в самых простейших случаях.

В связи с этим особое значение приобретают приближенные методы решения различных задач для дифференциальных уравнений в частных производных, систем дифференциальных уравнений в частных производных и интегральных уравнений или, как часто говорят, задач математической физики.

В настоящей главе мы и рассмотрим некоторые, наиболее распространенные методы решения задач математической физики. При этом мы ограничимся в основном методами решения задач для линейных дифференциальных уравнений в частных производных второго порядка с двумя независимыми переменными и линейными интегральными уравнениями, в которых искомая функция зависит только от одного независимого переменного. Изложение методов для случая произвольного числа переменных было бы связано с очень громоздкими записями, в то время как основные идеи методов, а также возникающие при их реализации трудности хорошо усматриваются в простейших случаях.

Что касается нелинейных уравнений, то хотя отдельные задачи для нелинейных уравнений и были разрешены, однако общая теория приближенных методов для нелинейных уравнений все еще отсутствует. В последнее время численным методам решения задач для нелинейных уравнений уделяется много внимания, но их разработка еще не достигла такого состояния, при котором их можно было бы включить в учебное пособие.

Как и в случае обыкновенных дифференциальных уравнений, приближенные методы решения различных задач для

дифференциальных уравнений в частных производных можно разбить на две группы:

1) методы, в которых приближенное решение получается в аналитической форме, например в виде отрезка некоторого ряда, и

2) методы, с помощью которых можно получить таблицу приближенных значений искомого решения в некоторых точках рассматриваемой области, - численные методы.

К первой группе относится прежде всего метод Фурье решения краевых задач для дифференциальных уравнений в частных производных, при применении которого точное решение получается в виде некоторого ряда, а за приближенное решение может быть принята сумма некоторого числа первых его членов. Метод Фурье решения классических задач математической физики подробно излагается в курсе математической физики, и мы на нем совсем не будем останавливаться. Из методов первой группы мы рассмотрим лишь вариационные методы решения краевых задач для уравнений в частных производных и близкий к ним метод Галеркина.

Наиболее широко распространенным методом численного решения задач для дифференциальных уравнений в частных производных является метод сеток, или метод конечных разностей, а также метод характеристик решения уравнений и систем уравнений гиперболического типа, который в сущности также является конечноразностным методом, только в этом методе дифференциальное уравнение в частных производных или система таких уравнений предварительно сводится к эквивалентной ей системе обыкновенных дифференциальных уравнений, которая и решается разностным методом. Описанию метода сеток для решения некоторых задач математической физики в основном и посвящена эта глава.

Особое место занимает метод прямых, который в зависимости от способа его реализации может быть отнесен как к той, так и к другой группе методов. В этом методе ищется приближенно решение дифференциального уравнения в частных производных вдоль некоторого семейства прямых. При этом вместо дифференциального уравнения в частных производных получается система обыкновенных дифференциальных уравнений. Если эта система решается в конечном виде, то мы получаем приближенное решение дифференциального уравнения в частных производных в виде системы функций, приближенно представляющих искомое решение вдоль рассматриваемых прямых. Если же система обыкновенных дифференциальных уравнений решается численными методами, то и приближенное решение уравнения в частных производных получается в виде таблицы, и в этом случае этот метод можно отнести к группе численных методов.

В последнем параграфе главы изложены методы приближенного решения линейных интегральных уравнений типа Фредгольма и Вольтерра.

В силу значительных трудностей, возникающих при приближенном решении дифференциальных уравнений в частных производных мы ограничимся при изложении из педагогических соображений только простейшими уравнениями и простейшими задачами для них, причем во многих случаях не приводятся доказательства сходимости, а также оценки погрешностей, если даже они существуют. Это отнюдь не означает, что описанные методы неприменимы для решения других более сложных задач.