Согласно формуле (9.29) параметры линейного тренда равны а = 1894/11 = 172,2 ц/га; b = 486/110 = 4,418 ц/га. Уравнение линейного тренда имеет вид:
у̂ = 172,2 + 4,418t , где t = 0 в 1987 г Это означает,что средний фактический и выравненный уровень, отнесенный к середине периода, т.е. к 1991 г., равен 172 ц с 1 ra a среднегодовой прирост составляет 4,418 ц/га в год
Параметры параболического тренда согласно (9.23) равны- b = 4,418; a = 177,75; с = -0,5571. Уравнение параболического тренда имеет вид у̃ = 177,75 + 4,418t - 0.5571t 2 ; t = 0 в 1991 г. Это означает, что абсолютный прирост урожайности замедляется в среднем на 2·0,56 ц/га в год за год. Сам же абсолютный прирост уже не является константой параболического тренда, а является средней величиной за период. В год, принятый за начало отсчета т.е. 1991 г., тренд проходит через точку с ординатой 77,75 ц/га; Свободный член параболического тренда не является средним уровнем за период. Параметры экспоненциального тренда вычисляются по формулам(9.32) и (9.33) lnа = 56,5658/11 = 5,1423; потенцируя, получаем а = 171,1; lnk = 2,853:110 = 0,025936; потенцируя, получаем k = 1,02628.
Уравнение экспоненциального тренда имеет вид: y̅ = 171,1·1,02628 t .
Это означает, что среднегодовой темп поста урожайности за период составил 102,63%. В точке принятК начало отсчета, тренд проходит точку с ординатой 171,1 ц/га.
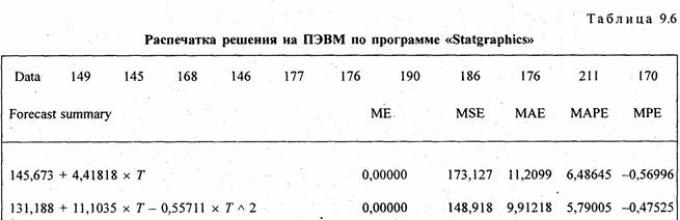
Рассчитанные по уравнениям трендов уровни записаны в трех последних графах табл. 9.5. Как видно по этим данным. расчетные значения уровней по всем трем видам трендов различаются ненамного, так как и ускорение параболы, и темп роста экспоненты невелики. Существенное отличие имеет парабола - рост уровней с 1995 г. прекращается, в то время как при линейном тренде уровни растут и далее, а при экспоненте их ост ускоряется. Поэтому для прогнозов на будущее эти три тренда неравноправны: при экстраполяции параболы на будущие годы уровни резко разойдутся с прямой и экспонентой, что видно из табл. 9.6. В этой таблицепредставлена распечатка решения на ПЭВМ по программе «Statgraphics» тех же трех трендов. Отличие их свободных членов от приведенных выше объясняется тем, что программа нумерует года не от середины, а от начала, так что свободные члены трендов относятся к 1986 г., для которого t = 0. Уравнение экспоненты на распечатке оставлено в логарифмированном виде. Прогноз сделан на 5 лет вперед, т.е. до 2001 г.. При изменении начала координат (отсчета времени) в уравнении параболы меняется и средний абсолютной прирост, параметр b. так как в результате отрицательного ускорения прирост все время сокращается, а его максимум - в начале периода. Константой параболы является только ускорение.
В строке «Data» приводятся уровни исходного ряда; «Forecast summary» означает сводные данные для прогноза. В следующих строках - уравнения прямой, параболы, экспоненты - в логарифмическом виде. Графа ME означает среднее расхождение между уровнями исходного ряда и уровнями тренда (выравненными). Для прямой и параболы это расхождение всегда равно нулю. Уровни экспоненты в среднем на 0,48852 ниже уровней исходного ряда. Точное совпадение возможно, если истинный тренд - экспонента; в данном случае совпадения нет, но различие, мало. Графа МАЕ -это дисперсия s 2 - мера колеблемости фактических уровней относительно тренда, о чем сказано в п. 9.7. Графа МАЕ - среднее линейное отклонение уровней от тренда по модулю (см. параграф 5.8); графа МАРЕ - относительное линейное отклонение в процентах. Здесь они приведены как показатели пригодности выбранного вида тренда. Меньшую дисперсию и модуль отклонения имеет парабола: она за период 1986 - 1996 гг. ближе к фактическим уровням. Но выбор типа тренда нельзя сводить лишь к этому критерию. На самом деле замедление прироста есть результат большого отрицательного отклонения, т. е. неурожая в 1996 г.
Вторая половина таблицы - это прогноз уровней урожайности по трем видам трендов на годы; t = 12, 13, 14, 15 и 16 от начала отсчета (1986 г.). Прогнозируемые уровни по экспоненте вплоть до 16-го года ненамного выше,.чем по прямой. Уровни тренда-параболы - снижаются, все более расходясь с другими трендами.
Как видно в табл. 9.4, при вычислении параметров тренда уровни исходного ряда входят с разными весами - значениями t p и их квадратов. Поэтому влияние колебаний уровней на параметры тренда зависит от того, на какой номер года приходится урожайный либо неурожайный год. Если резкое отклонение приходится на год с нулевым номером (t i = 0 ), то оно никакого влияния на параметры тренда не окажет, а если попадет на начало и конец ряда, то повлияет сильно. Следовательно, однократное аналитическое выравнивание неполно освобождает параметры тренда от влияния колеблемости, и при сильных колебаниях они могут быть сильно искажены, что в нашем примере случилось с параболой. Для дальнейшего исключения искажающего влияния колебаний на параметры тренда следует применить метод многократного скользящего выравнивания.
Этот прием состоит в том, что параметры тренда вычисляются не сразу по всему ряду, а скользящим методом, сначала за первые т периодов времени или моментов, затем за период от 2-го до т + 1, от 3-го до (т + 2)-го уровня и т.п. Если число исходных уровней ряда равно п, а длина каждой скользящей базы расчета параметров равна т, то число таких скользящих баз t или отдельных значений параметров, которые будут по ним определены, составит:
L = п + 1 - т.
Применение методики скользящего многократного выравнивания рассматривать, как видно из приведенных расчетов, возможно только при достаточно большом числе уровней ряда, как правило 15 и более. Рассмотрим эту методику на примере данных табл. 9.4 -динамики цен на нетопливные товары развивающихся стран, что опять же дает возможность читателю участвовать в небольшом научном исследовании. На этом же примере продолжим и методику прогнозирования в разделе 9.10.
Если вычислять в нашем ряду параметры по 11 -летним периодам (по 11 уровням), то t = 17 + 1 - 11 = 7. Смысл многократного скользящего выравнивания в том, что при последовательных сдвигах базы расчета параметров на концах ее и в середине окажутся разные уровни с разными по знаку и величине отклонениями от тренда. Поэтому при одних сдвигах базы параметры будут завышаться, при других - занижаться, а при последующем усреднении значений параметров по всем сдвигам базы расчета произойдет дальнейшее взаимопогашение искажений параметров тренда колебаниями уровней.
Многократное скользящее выравнивание не только позволяет получить более точную и надежную оценку параметров тренда, но и осуществить контроль правильности выбора типа уравнения тренда. Если окажется, что ведущий параметр тренда, его константа при расчете по скользящим базам не беспорядочно колеблется, а систематически изменяет свою величину существенным образом, значит, тип тренда был выбран неверно, данный параметр константой не является.
Что касается свободного члена при многократном выравнивании, то нет необходимости и, более того, просто неверно вычислять его величину как среднюю по всем сдвигам базы, ибо при таком способе отдельные уровни исходного ряда входили бы в расчет средней с разными весами, и сумма выравненных уровней разошлась бы с суммой членов исходного ряда. Свободный член тренда - это средняя величина уровня за период, при условии отсчета времени от середины периода. При отсчете от начала, если первый уровень t i = 1, свободный член будет равен: a 0 = у̅ - b ((N-1)/2). Рекомендуется длину скользящей базы расчета параметров тренда выбирать не менее 9-11 уровней, чтобы в достаточной мере погасить колебания уровней. Если исходный ряд очень длинный, база может составлять до 0,7 - 0,8 его длины. Для устранения влияния долго-периодических (циклических) колебаний на параметры тренда, число сдвигов базы должно быть равно или кратно длине цикла колебаний. Тогда начало и конец базы будут последовательно «пробегать» все фазы цикла и при усреднении параметра по всем сдвигам его искажения от циклических колебаний будут взаимопогашаться. Другой способ - взять длину скользящей базы, равной длине цикла, чтобы начало базы и конец базы всегда приходились на одну и ту же фазу цикла колебаний.
Поскольку по данным табл. 9.4, уже было установлено, что тренд имеет линейную форму, проводим расчет среднегодового абсолютного прироста, т. е. параметра b уравнения линейного тренда скользящим способом по 11-летним базам (см. табл. 9.7). В ней же приведен расчет данных, необходимых для последующего изучения колеблемости в параграфе 9.7. Остановимся подробнее на методике многократного выравнивания по скользящим базам. Рассчитаем параметр b по всем базам:
Лекция 4. ОСНОВНЫЕ ТИПЫ ТЕНДЕНЦИЙ И УРАВНЕНИЙ ТРЕНДА
В главе 2 было рассмотрено понятие о тенденции временного ряда, т.е. тенденции динамики развития изучаемого показате-ля. Задача данной главы состоит в том, чтобы рассмотреть ос-новные типы таких тенденций, их свойства, отражаемые с большей или меньшей степенью полноты уравнением линии тренда. Укажем при этом, что в отличие от простых систем ме-ханики тенденции изменения показателей сложных социальных, экономических, биологических и технических систем только с некоторым приближением отражаются тем или иным уравне-нием, линией тренда.
В данной главе рассматриваются далеко не все известные в математике линии и их уравнения, а лишь набор их сравнитель-но простых форм, который мы считаем достаточным для ото-бражения и анализа большинства встречающихся на практике тенденций временных рядов. При этом желательно всегда вы-бирать из нескольких типов линий, достаточно близко выра-жающих тенденцию, более простую линию. Этот «принцип простоты» обоснован тем, что чем сложнее уравнение линии тренда, чем большее число параметров оно содержит, тем при равной степени приближения труднее дать надежную оценку этих параметров по ограниченному числу уровней ряда и тем больше ошибка оценки этих параметров, ошибки прогнозиру-емых уровней.
4.1. Прямолинейный тренд и его свойства
Самым простым типом линии тренда является прямая ли-ния, описываемая линейным (т.е. первой степени) уравнением тренда:
Где 
-
выровненные, т.е. лишенные колебаний, уровни тренда для лет с номером i;
а - свободный член уравнения, численно равный среднему выровненному уровню для момента или периода времени, принятого за начало отсчета, т.е. для
t = 0;
b - средняя величина изменения уровней ряда за единицу из-менения времени;
ti - номера моментов или периодов времени, к которым от-носятся уровни временного ряда (год, квартал, месяц, дата).
Среднее изменение уровней ряда за единицу времени - глав-ный параметр и константа прямолинейного тренда. Следова-тельно, этот тип тренда подходит для отображения тенденции примерно равномерных изменений уровней: равных в среднем абсолютных приростов или абсолютных сокращений уровней за равные промежутки времени. Практика показывает, что та-кой характер динамики встречается достаточно часто. Причи-на близких к равномерному абсолютных изменений уровней ряда состоит в следующем: многие явления, как, например, урожай-ность сельскохозяйственных культур, численность населения региона, города, сумма дохода населения, среднее потребление какого-либо продовольственного товара и др., зависят от боль-шого числа различных факторов. Одни из них влияют в сторо-ну ускоренного роста изучаемого явления, другие - в сторону замедленного роста, третьи - в направлении сокращения уров-ней и т.д. Влияние разнонаправленных и разноускоренных (за-медленных) сил факторов взаимно усредняется, частично взаимно погашается, а равнодействующая их влияний приобре-тает характер, близкий к равномерной тенденции. Итак, равно-мерная тенденция динамики (или застоя) - это результат сложения влияния большого количества факторов на изменение изучаемого показателя.
Графическое изображение прямолинейного тренда - прямая линия в системе прямоугольных координат с линейным (ариф-метическим) масштабом на обеих осях. Пример линейного тренда дан на рис. 4.1.
Абсолютные изменения уровней в разные годы не были точно одинаковыми, но общая тенденция сокращения численности занятых в народном хозяйстве очень хорошо отражает-ся прямолинейным трендом. Его параметры вычислены в гл. 5 (табл. 5.3).
Основные свойства тренда в форме прямой линии таковы:
Равные изменения за равные промежутки времени;
Если средний абсолютный прирост - положительная вели-чина, то относительные приросты или темпы прироста посте-пенно уменьшаются;
Если среднее абсолютное изменение - отрицательная вели-чина, то относительные изменения или темпы сокращения по-степенно увеличиваются по абсолютной величине снижения к предыдущему уровню;
Если тенденция к сокращению уровней, а изучаемая вели-чина является по определению положительной, то среднее изме-нение b не может быть больше среднего уровня а;
При линейном тренде ускорение, т.е. разность абсолютных изменений за последовательные периоды, равно нулю.
Свойства линейного тренда иллюстрирует табл. 4.1. Урав-нение тренда: = 100 +20 *ti.
Показатели динамики при наличии тенденции сокращения уровней приведены в табл. 4.2.
Таблица 4.1
Показатели динамики при линейном тренде к увеличению уровней = 100 +20 *ti.
| Номер периода ti | Уровень | | Темпы (цеп-ные), % | Ускоре-ние |
| 1 | 120 | +20 | 120,0 | - |
| 2 | 140 | +20 | 116,7 | 0 |
| 3 | 160 | +20 | 114,3 | 0 |
| 4 | 180 | +20 | 112,5 | 0 |
| 5 | 200 | +20 | 111,1 | 0 |
| 6 | 220 | +20 | 110,0 | 0 |
Таблица 4.2
Показатели динамики при линейном тренде сокращения уровней: = 200 -20 *ti.
| Номер периода ti | Уровень | Абсолютное изме-нение к предыду-щему периоду | Темп к предыдущему периоду, % | Ускоре-ние |
| 1 | 180 | -20 | 90,0 | - |
| 2 | 160 | -20 | 88,9 | 0 |
| 3 | 140 | -20 | 87,5 | 0 |
| 4 | 120 | -20 | 85,7 | 0 |
| 5 | 100 | -20 | 83,3 | 0 |
| 6 | 80 | -20 | 80,0 | 0 |
^ 4.2. Параболический тренд и его свойства
Под названием параболического будем иметь в виду тренд, выраженный параболой II порядка с уравнением
=a+b*t+c*t 2 .
Параболы III порядка и более высоких порядков редко приме-нимы для выражения тенденции динамики и слишком сложны для получения надежных оценок параметров при ограничен-ной длине временного ряда. Прямую линию, с точки зрения ма-тематики, можно также считать одним из видов парабол - параболой I порядка, которая уже рассмотрена ранее.
Значения (смысл, сущность) параметров параболы II поряд-ка таковы: свободный член а - это средний (выровненный) уро-вень тренда на момент или период, принятый за начало отсчета времени, т.е. t = 0; b - это средний за весь период среднегодовой прирост, который уже не является константой, а изменяется рав-номерно со средним ускорением, равным 2 с, которое и служит константой, главным параметром параболы II порядка.
Следовательно, тренд в форме параболы II порядка при-меняется для отображения таких тенденций динамики, кото-рым свойственно примерно постоянное ускорение абсолютных изменений уровней. Процессы такого рода встречаются на практике гораздо реже, чем процессы с равномерным измене-нием, но, с другой стороны, любое отклонение процесса от строго равномерного прироста (или сокращения) уровней можно интерпретировать как наличие ускорения. Более того, существует строгое математическое правило: чем выше поря-док параболы, тем ближе линия тренда к уровням исходного временного ряда. Если это правило довести до крайнего пре-дела, то любой ряд из п уровней может быть точно отображен параболой (п -1)-го порядка! (Через любые две точки прохо-дит одна прямая, через три точки - одна парабола II порядка и т.д.) Такое «приближение» линии тренда к эмпирическому ряду, содержащему как тенденцию, так и колебания, нельзя считать достижением научного анализа. Напротив, применяя параболу более высокого порядка там, где сущность процес-са этого не требует, а только ради уменьшения остаточной суммы отклонений (или их квадратов) отдельных уровней от тренда, исследователь уходит от цели, смешивая тренд с коле-баниями.
ПараболаII порядка, как уравнение тренда, применяется к различным процессам, которые на некотором, как правило не-продолжительном, этапе развития имеют примерно постоян-ное ускорение абсолютного прироста уровней. Такими бывают рост населения отдельных городов или регионов, ускоренное увеличение объема продукции в фазе циклического подъема, как, например, динамика экспорта Японии в 1988-1995 гг. на рис. 4.2.
Рис. 4.2. Динамика экспорта Японии
Расчет уравнения этой параболы приведен в гл. 5. Основные свойства тренда в форме параболы II порядка та-ковы:
1) неравные, но равномерно возрастающие или равномерно убывающие абсолютные изменения за равные промежутки вре-мени;
2) парабола, рассматриваемая относительно ее математи-ческой формы, имеет две ветви: восходящую с увеличением уровней признака и нисходящую с их уменьшением. Но отно-сительно статистики по содержанию изучаемого процесса из-менений трендом, выражающим определенную тенденцию развития, чаще всего можно считать только одну из ветвей:
Либо восходящую, либо нисходящую. В особых, более конк-ретных, ситуациях мы не отрицаем возможности объединения обеих ветвей в единый тренд;
3) так как свободный член уравнения а как значение показа-теля в начальный момент (период) отсчета времени, как правило, величина положительная, то характер тренда определяется знаками параметров b и с:
А) при b >0 и с>0 имеем восходящую ветвь, т.е. тенденцию к ускоренному росту уровней;
Б) при b <0 и с<0 имеем нисходящую ветвь - тенденцию к ускоренному сокращению уровней;
В) при b > 0 и с<0 имеем либо восходящую ветвь с замедляю-щимся ростом уровней, либо обе ветви параболы, восходящую и нисходящую, если их по существу можно считать единым про-цессом;
Г) при b <0 и с>0 имеем либо нисходящую ветвь с замедляю-щимся сокращением уровней, либо обе ветви - нисходящую и восходящую, если их можно считать единой тенденцией;
4) при параболической форме тренда, в зависимости от со-отношений между его параметрами, цепные темпы изменений могут либо уменьшаться, либо некоторое время возрастать, но при достаточно длительном периоде рано или поздно темпы роста обязательно начинают уменьшаться, а темпы сокращения уровней при b <0 и с<0 обязательно начинают возрастать (по абсолютной величине относительного изменения).
Ввиду ограниченного объема учебника рассмотрим не все четыре случая параболических трендов, а лишь два первых (табл. 4.3 и 4.4).
Таблица 4.3
Показатели динамики при параболическом тренде,
| Номер периода ti | Уровень  | Абсолютное изменение | | Ускоре-ние |
| 1 | 122 | +22 | 122,0 | - |
| 2 | 148 | +26 | 121,3 | +4 |
| 3 | 178 | +30 | 120,3 | +4 |
| 4 | 212 | +34 | 119,1 | +4 |
| 5 | 250 | +38 | 117,9 | +4 |
| 6 | 292 | +42 | 116,8 | +4 |
^ Таблица 4.4
Показатели динамики при параболическомтренде,
| Номер перио-да | Уро-вень | Абсо-лютные измене-ния | Цепные темпы, % к предыдущему периоду | Уско-рение | Цепное относи-тельное измене-ние, % к преды-дущему периоду |
| 1 | 178 | -22 | 89,0 | - | -11,0 |
| 2 | 152 | -26 | 85,4 | -4 | -14,6 |
| 3 | 122 | -30 | 80,3 | -4 | -19,7 |
| 4 | 88 | -34 | 72,1 | -4 | -27,9 |
| 5 | 50 | -38 | 56,8 | -4 | -43,2 |
| 6 | 8 | -42 | 16,0 | -4 | -84,0 |
В тех случаях, когда по существу изучаемого процесса до-пустимо считать единым трендом обе ветви параболы, пред-ставляет большой интерес решение задачи о нахождении того периода или момента времени, когда уровень тренда достигает максимума (когда b >0, с<0) или минимума (если b <0, с>0). Эк-стремальная точка параболы
= а
+ bt
+ ct
2
достигается при ну-левом значении первой производной:
^ 4.3. Экспоненциальный тренд и его свойства
Экспоненциальным трендом
называют тренд, выраженный уравнением: .
Свобод-ный член экспоненты а
равен выровненному уровню, т.е. уров-ню тренда в момент или период, принятый за начало отсчета времени, т.е. при t
=
0.
Основной параметр экспоненциального тренда k
является постоянным темпом изменения уровней (цен-ным). Если k
>
1,
имеем тренд с возрастающими уровнями, при-чем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными всех более высо-ких порядков. Если k
<
1, то имеем тренд, выражающий тенден-цию постоянного, но замедляющегося сокращения уровней, причем замедление непрерывно усиливается. Экстремума экс-понента не имеет и при 
стремится либо к 
при k
>
1, либо к 0 при k
<
1.
Экспоненциальный тренд характерен для процессов, разви-вающихся в среде, не создающей никаких ограничений для рос-та уровня. Из этого следует, что на практике он может развиваться только на ограниченном промежутке времени, так как любая среда рано или поздно создает ограничения, любые ресурсы со временем исчерпаемы. Однако практика показала что, например, численность населения Земли на протяжении 1950-1985 гг. возрастала примерно по экспоненте со среднего-довым темпом роста k = 1,018 и за это время возросла вдвое - с 2,5 до 5 млрд. чел. (рис. 4.3). В настоящее время темп роста насе-ления постепенно уменьшается.
Экспоненциальный рост объема реализации и производства происходит при возникновении новых видов продукции и их освоении промышленностью: при появлении цветных телеви-зоров, видеомагнитофонов, пейджеров и т.п., но когда произ-водство начинает наполнять рынок, приближаться к спросу, экспоненциальный рост прекращается.
Рис. 4.3. Рост народонаселения Земли
Расчет экспоненциального тренда дан в гл. 5. Основные свойства экспоненциального тренда:
1. Абсолютные изменения уровней тренда пропорциональ-ны самим уровням.
2. Экспонента экстремумов не имеет: при k > 1 тренд стремит-ся к +, при k < 1 тренд стремится к нулю.
3. Уровни тренда представляют собой геометрическую про-грессию: уровень периода с номером t = т есть a * k m .
4. При k > 1 тренд отражает ускоряющийся неравномерно рост уровней, при k < 1 тренд отражает замедляющееся неравномерно уменьшение уровней. Поведение основных показателей дина-мики в этих случаях рассмотрено в табл. 4.5 и 4.6.
В табл. 4.5 и 4.6 в последней графе приведены редко приме-няемые показатели динамики III порядка: ускорение (или при-рост) ускорения и замедление ускорения. Эти абсолютные показатели даны для наглядного пояснения главного отличия экспоненциального тренда от парабол любого порядка: экспо-нента не имеет постоянных производных любого порядка по времени. Постоянен только цепной темп изменения.
| Номер периода  | Уровень | Абсолютные изменения (цепные) | Цепные темпы, % к предыдущему периоду | Ускорение | Прирост ускорения к предыдущему периоду |
| 1 | 120,00 | +20,00 | 120 | - | - |
| 2 | 144,00 | +24,00 | 120 | +4,00 | - |
| 3 | 172,80 | +28,80 | 120 | +4,80 | +0,80 |
| 4 | 207,36 | +34,56 | 120 | +4,76 | +0,96 |
| 5 | 248,83 | +41,47 | 120 | +6,81 | +1,15 |
| 6 | 298,60 | +49,77 | 120 | +8,30 | +1,39 |
| Номер периода | Уровень | Абсолютные изменения (цепные) | Цепные темпы, % к предыдущему периоду | Ускорение | Замедление ускорения |
| 1 | 160,00 | 40,00 | 80 | - | - |
| 2 | 128,0 | -32,00 | 80 | +8,00 | - |
| 3 | 102,40 | -25,60 | 80 | +6,40 | -1,60 |
| 4 | 81,92 | -20,48 | 80 | +5,12 | -1,28 |
| 5 | 65,54 | -16,38 | 80 | +4,10 | -1,02 |
| 6 | 52,43 | -13,11 | 80 | +3,27 | -0,83 |
Читатель может заинтересоваться и таким вопросом: как на-звать тенденцию динамики, при которой и темп изменения был бы непостоянен, а имел постоянное абсолютное или относи-тельное изменение, например, уравнение типа 
или 
и т.д. Подобные «гиперэкспоненты» не применяют-ся статистикой, ибо любой, сколь угодно быстрый, сколь угодно ускоряющийся рост может быть отображен обычной экспонентой - стоит лишь уменьшить период, за который происходит возрастание (или сокращение) уровней в k
раз. По своему суще-ству экспоненциальное развитие процесса и есть предельно воз-можное, предельно благоприятное по условиям развития, так как оно осуществляется в среде, не ограничивающей развитие данного процесса. Но следует помнить, что это происходит толь-ко до определенного времени, так как каждая среда, каждый ре-сурс в природе ограничен. Единственный спорный в науке процесс, по которому до сих пор нет доказательства ограничен-ности его во времени, - это экспоненциальное замедляющееся расширение Вселенной. Ограничено ли оно и сменится ли со временем сжатием или будет продолжаться бесконечно, зави-сит от значения средней плотности вещества и излучения во Вселенной, которую пока науке установить не удалось, ибо не все формы существования вещества и полей науке извест-ны. Зато интересно знать, что самый фундаментальный про-цесс, охватывающий всю известную Вселенную, уже, по крайней мере, 12-15 млрд. лет развивается по экспоненте.
^ 4.4. Гиперболический тренд и его свойства
Из различных форм гипербол рассмотрим только наиболее простую: 
Если основной параметр гиперболы b
>0,
то этот тренд вы-ражает тенденцию замедляющегося снижения уровней и при 
..
Таким образом, свободный член гиперболы - это предел, к которому стремится уровень тренда.
Такая тенденция наблюдается, например (рис. 4.4), при изу-чении процесса снижения затрат любого ресурса (труда, мате-риалов, энергии) на единицу данного вида продукции или ее себестоимости в целом. Затраты ресурса не могут стремиться к нулю, значит, экспонента не соответствует сущности процесса; нужно применить гиперболическую формулу тренда.
Если параметр b <0, то с возрастанием t , т.е. с течением вре-мени, уровни тренда возрастают и стремятся к величине а при .
Такой характер динамики присущ, например, показателям КПД двигателей или иных преобразователей энергии (трансфор-матор тока, фотоэлемент и т.п.). По мере развития научно-тех-нического прогресса эти КПД постепенно повышаются, но никогда не могут превысить определенного предела для каждо-го типа двигателя и не могут превысить 100% в принципе для любого преобразователя энергии. При расчете гиперболического тренда нельзя нумеровать года от середины ряда, так как значения 1/ti должны быть всегда положительными.
Основные свойства гиперболического тренда:
1. Абсолютный прирост или сокращение уровней, ускоре-ние абсолютных изменений, темп изменения - все эти показате-ли не являются постоянными. При b >0 уровни замедленно уменьшаются, отрицательные абсолютные изменения, а также положительные ускорения тоже уменьшаются, цепные темпы из-менения растут и стремятся к 100%.
Рис. 4.4. Динамика расхода условного топлива на производство электроэнергии (г на 1 кВт-ч) на электростанциях региона
2. При b <0 уровни замедленно возрастают, положительные абсолютные изменения, а также отрицательные ускорения и цеп-ные темпы роста замедленно уменьшаются, стремясь к 100%.
Как видим, гиперболический тренд описывает в любом слу-чае тенденцию такого процесса, показатели которого со време-нем затухают, т.е. происходит переход от движения к застою. Иллюстрацией этих свойств может служить табл. 4.7.
Таблица 4.7
Показатели динамики при гиперболическом тренде: 
| Номер периода | Уровень | Абсолютные изменения (цепные) | Цепные темпы, % к предыдущему периоду | Ускорение |
| 1 | 200,0 | - | - | - |
| 2 | 150,0 | -50,0 | 75,0 | - |
| 3 | 133,0 | -16,7 | 88,9 | +33,3 |
| 4 | 125,0 | -8,3 | 93,8 | +8,4 |
| 5 | 120,0 | -5,0 | 96,0 | +3,3 |
| 6 | 116,7 | -3,3 | 97,2 | +1,7 |
^ 4.5. Логарифмический тренд и его свойства
Если изучаемый процесс приводит к замедлению роста ка-кого-то показателя, но при этом рост не прекращается, не стремится к какому-либо ограниченному пределу, то гипербо-лическая форма тренда уже не подходит. Тем более не подходит парабола с отрицательным ускорением, по которой замедляю-щийся рост перейдет со временем в снижение уровней. В указан-ном случае тенденция изменения лучше всего отображается логарифмической формой тренда: = a + b ln .
Логарифмы возрастают значительно медленнее, чем сами числа (номера периодов ), но рост логарифмов неограничен. Подбирая начало отсчета периодов (моментов) времени, мож-но найти такую скорость снижения абсолютных изменений, ко-торая наилучшим образом отвечает фактическому временному ряду.
Примером тенденций, соответствующих логарифмическому тренду, может служить динамика рекордных достижений в спорте: известно, что увеличение на 1 см рекорда прыжка в вы-соту или снижение на 0,1 с времени бега на 200 или 400 м требует все больших и больших затрат времени, каждый рекорд дается все большим и большим трудом. В то же время нет и «вечных» рекордов, все спортивные достижения улучшаются, но медлен-нее и медленнее, т.е. по логарифмическому тренду. Нередко та-кой же характер динамики присущ на отдельных этапах развития динамике урожайности или валового сбора какой-то культуры в данном регионе, пока новое агротехническое достижение не при-даст снова тенденции ускорения, что иллюстрирует рис. 4.5.
Конечно, характер тенденции маскируется колебаниями, но видно, что рост валового сбора замедляется. Это показывают и средние уровни сбора чая:
За 1978-1983 гг. средний сбор равен 333 тыс. т;
За 1984-1989 гг. средний сбор равен 483 тыс. т, рост на 150 тыс.т;
За 1990-1994 гг. средний сбор равен 566 тыс. т, рост на 83 тыс.т.
На рис. 4.5 для убедительности нанесен и логарифмический тренд, расчет
Рис. 4.5. Динамика валового сбора чая в Китае
Которого дан в гл. 5. Заметны также 5-6-летние циклические колебания валового сбора чая.
Основные свойства логарифмического тренда:
1. Если b >0, то уровни возрастают, но с замедлением, а если b <0, то уровни тренда уменьшаются, тоже с замедлением.
2. Абсолютные изменения уровней по модулю всегда умень-шаются со временем.
3. Ускорения абсолютных изменений имеют знак, противо-положный самим абсолютным изменениям, а по модулю посте-пенно уменьшаются.
4. Темпы изменения (цепные) постепенно приближаются к 100% при .
Можно сделать общий вывод о том, что логарифмический тренд отражает, так же как и гиперболический тренд, посте-пенно затухающий процесс изменений. Различие состоит в том, что затухание по гиперболе происходит быстро при приближе-нии к конечному пределу, а при логарифмическом тренде зату-хающий процесс продолжается без ограничения гораздо медленнее.
^ 4.6. Логистический тренд и его свойства
Логистическая форма тренда подходит для описания такого процесса, при котором изучаемый показатель проходит полный цикл развития, начиная, как правило, от нулевого уровня, сна-чала медленно, но с ускорением возрастая, затем ускорение ста-новится нулевым в середине цикла, т.е. рост происходит по линейному тренду, затем, в завершающей части цикла, рост за-медляется по гиперболе по мере приближения к предельному значению показателя.
Примером такого цикла динамики может служить измене-ние доли грамотного населения в стране, например в России, с 1800 г. до наших дней, или изменение доли семей, имеющих те-левизоры, примерно с 1945 до 2000 г. в России, доли жилищ в городах, имеющих горячее водоснабжение или центральное ото-пление (процесс, еще не законченный). В некоторых зарубеж-ных программах для компьютеров логистическая кривая называется S-образной кривой.
Можно, конечно, логистическую тенденцию считать объе-динением трех разных по типу тенденций: параболической с ускоряющимся ростом на первом этапе, линейной - на втором и гиперболической с замедляющимся ростом - на третьем этапе. Но есть доводы и в пользу рассмотрения всего цикла развития как особого единого типа тенденции со сложными, переменными свойствами, но постоянным направлением из-менений в сторону увеличения уровней в рассмотренных нами примерах или уменьшения уровней, если взять противополож-ный процесс - сокращение доли неграмотных среди населе-ния, доли жилищ, не оборудованных газоснабжением или центральным отоплением, и т.д.
Рассмотрение таких временных рядов, как проявление еди-ной логистической тенденции, позволяет уже на первом этапе рассчитать всю траекторию развития, определить сроки пере-хода от ускоренного роста к замедленному, что чрезвычайно важно при планировании производства или реализации нового вида товара, спрос на который будет проходить все этапы логи-стической тенденции вплоть до насыщения рынка. Так, напри-мер, обеспеченность населения в России автомобилями в конце 1980-х годов находилась на начальном этапе логистической кри-вой, и это означало, что предстоит еще ряд лет или даже десяти-летий ускоренного роста спроса. В то же время обеспеченность фотоаппаратами уже достигла этапа замедления роста, и это означало, что расширять производство или импорт прежних типов фотоаппаратов не следует. Расширение их рынка возмож-но было только для принципиально новых типов фотоаппара-тов, насыщенность которыми еще находится в самом начале первого этапа.
В вышеописанном диапазоне изменения уровней, т.е. от нуля до единицы, уравнение логистического тренда имеет вид:
должно быть примерно равно -10. Чем больше 
, тем быст-рее будут снижаться уровни, например, при = -10; = 1, уже при = 20 уровни снизятся почти до нуля.
Если же диапазон изменения уровней ограничен не нулем и единицей, а любыми значениями, определяемыми исходя из су-щества задачи, обозначаемыми 
то формула логис-тического тренда принимает вид:
Как видно из табл. 4.8, абсолютные изменения нарастают до середины периода, затем уменьшаются. Все они положитель-ны. Ускорения сначала возрастают, а после середины периода снижаются, становятся отрицательными, но уменьшаются по мо-дулю. Сумма положительных и отрицательных ускорений при-ближенно равна нулю (если ряд продлить от - до +, то сумма их точно равна нулю). Темпы роста возрастают до конца пер-вой половины ряда, затем снижаются. Если ряд достаточно длин-ный, то темпы начинаются со 100 % и завершаются на 100%.
Таблица 4.8
Показатели динамики при логистическом тренде:
| Номер периода | Уровень | Абсолютные изме-нения к предыдуще-му периоду | Ускоре-ние | Темп роста к предыдущему периоду, % |
| 0 | 51,0 | - | - | - |
| 1 | 54,4 | +3,4 | - | 106,7 |
| 2 | 67,9 | +13,5 | +10,1 | 124,8 |
| 3 | 106,6 | +38,7 | +25,2 | 157,0 |
| 4 | 159,7 | +53,1 | +14,4 | 149,8 |
| 5 | 188,6 | +28,8 | -24,2 | 118,1 |
| 6 | 197,3 | +8,7 | -20,2 | 104,6 |
| 7 | 199,4 | +2,1 | -6,6 | 101,1 |
При логистическом тренде со снижающимися уровнями по-казатели динамики изменяются в следующем порядке: отрица-тельные абсолютные изменения по модулю возрастают до середины ряда и снижаются к концу, стремясь к нулю при . Ускорения в первой половине периода отрицательные и по мо-дулю возрастающие; во второй половине периода ускорения положительные и уменьшающиеся в пределе до нуля. Темпы изменений все меньше 100%, в конце первой половины периода наименьшие, во второй половине возрастающие с замедлением до 100% в пределе. Графическое изображение логистического тренда приведено на рис. 5.2.
ПРИМЕР . Статистическое изучение динамики численности населения.
С помощью цепных, базисных, средних показателей динамики оцените изменение численности, запишите выводы.
С помощью метода аналитического выравнивания (по прямой и параболе, определив коэффициенты с помощью МНК) выявите основную тенденцию в развитии явления (численность населения Республики Коми). Оцените качество полученных моделей с помощью ошибок и коэффициентов аппроксимации.
Определите коэффициенты линейного и параболического трендов с помощью средств «Мастера диаграмм». Дайте точечный и интервальный прогнозы численности на 2010 г. Запишите выводы.
Метод аналитического выравнивания а) Линейное уравнение тренда имеет вид y = bt + a 1. Находим параметры уравнения методом наименьших квадратов . Используем способ отсчета времени от условного начала. Система уравнений МНК для линейного тренда имеет вид: a 0 n + a 1 ∑t = ∑y a 0 ∑t + a 1 ∑t 2 = ∑y t
Для наших данных система уравнений примет вид: 10a 0 + 0a 1 = 10400 0a 0 + 330a 1 = -4038 Из первого уравнения выражаем а 0 и подставим во второе уравнение Получаем a 0 = -12.236, a 1 = 1040 Уравнение тренда: y = -12.236 t + 1040
Оценим
качество уравнения тренда с помощью
ошибки абсолютной аппроксимации.
Ошибка
аппроксимации в пределах 5%-7% свидетельствует
о хорошем подборе уравнения тренда к
исходным данным.
б) выравнивание по параболе Уравнение тренда имеет вид y = at 2 + bt + c 1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: a 0 n + a 1 ∑t + a 2 ∑t 2 = ∑y a 0 ∑t + a 1 ∑t 2 + a 2 ∑t 3 = ∑yt a 0 ∑t 2 + a 1 ∑t 3 + a 2 ∑t 4 = ∑yt 2
Для наших данных система уравнений имеет вид 10a 0 + 0a 1 + 330a 2 = 10400 0a 0 + 330a 1 + 0a 2 = -4038 330a 0 + 0a 1 + 19338a 2 = 353824 Получаем a 0 = 1.258, a 1 = -12.236, a 2 = 998.5 Уравнение тренда: y = 1.258t 2 -12.236t+998.5
Ошибка
аппроксимации для параболического
уравнения тренда.
Поскольку
ошибка меньше 7%, то данное уравнение
можно использовать в качестве тренда.
Минимальная ошибка аппроксимации при выравнивании по параболе. К тому же коэффициент детерминации R 2 выше чем при линейной. Следовательно, для прогнозирования необходимо использовать уравнение по параболе.
Интервальный
прогноз.
Определим среднеквадратическую
ошибку прогнозируемого показателя.
m
= 1 - количество влияющих факторов в
уравнении тренда.
Uy = y n+L ±
K
где
L
- период упреждения; у n+L -
точечный прогноз по модели на (n + L)-й
момент времени; n - количество наблюдений
во временном ряду; Sy - стандартная ошибка
прогнозируемого показателя; T табл -
табличное значение критерия Стьюдента
для уровня значимости α и для числа
степеней свободы, равного n-2
.
По
таблице Стьюдента находим
Tтабл
T табл (n-m-1;α/2)
= (8;0.025) = 2.306
Точечный прогноз, t = 10:
y(10) = 1.26*10 2 -12.24*10
+ 998.5 = 1001.89 тыс. чел.
1001.89
- 71.13 = 930.76 ; 1001.89 + 71.13 = 1073.02
Интервальный
прогноз:
t = 9+1 = 10: (930.76;1073.02)
Линейное уравнение тренда имеет вид y = at + b.
Параметры уравнений функции тренда находят с помощью теории корреляции методом наименьших квадратов.
1.Метод наименьших квадратов.
Метод наименьших квадратов МНК), является одним из способов противостоять ошибкам измерений.(Как в Физике погрешность отклонений)
Этот метод как правило используют для нахождения параметров уравнений (Линий, гипербол парабол и т.д.)
Этот способ заключается в минимизации суммы квадратов отклонений.
Смысл МНК можно выразить через вот этот график
2. Анализ точности определения оценок параметров уравнения тренда(по таблице стьюдента находим ТТабл и делаем интервальный прогноз,т.е. выявляем реднеквадратическую ошибку)
3.Проверка гипотез относительно коэффициентов линейного уравнения тренда(статистика критерий стьюдента,фишера)
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция)
Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
Проверка наличия гетероскедастичности
.
1) Методом графического анализа остатков
.
В этом случае по оси абсцисс откладываются значения объясняющей переменной X, а по оси ординат либо отклонения e i , либо их квадраты e 2 i .
Если имеется определенная связь между отклонениями, то гетероскедастичность имеет место. Отсутствие зависимости скорее всего будет свидетельствовать об отсутствии гетероскедастичности.
2) При помощи теста ранговой корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена.
36. Методы измерения устойчивости тенденций динамики (коэффициент рангов Спирмена).
Понятие «устойчивость» используется в весьма различных смыслах. По отношению кстатистическому изучению динамики мы рассмотрим два аспекта этого понятия: 1) устойчивостькак категория, противоположная колеблемости; 2) устойчивость направленности изменений, т.е. устойчивость тенденции.
Устойчивость во втором смысле характеризует не сами по себе уровни, а процесс ихнаправленного изменения. Можно узнать, например, насколько устойчив процесс сокращенияудельных затрат ресурсов на производство единицы продукции, является ли устойчивойтенденция снижения детской смертности и т. д. С этой точки зрения полной устойчивостьюнаправленного изменения уровней динамического ряда следует считать такое изменение, впроцессе которого каждый следующий уровень либо выше всех предшествующих (устойчивыйрост), либо ниже всех предшествующих (устойчивое снижение). Всякое нарушение строгоранжированной последовательности уровней свидетельствует о неполной устойчивостиизменений.
Из определения понятия устойчивости тенденции вытекает и метод построения ее показателя.В качестве показателя устойчивости можно использовать коэффициент корреляции рангов Ч.Спирмэна (Spearman) - rx.
где п - число уровней;
I - разность рангов уровней и номеров периодов времени.
При полном совпадении рангов уровней, начиная с наименьшего, и номеров периодов (моментов)времени по их хронологическому порядку коэффициент корреляции рангов равен +1. Этозначение соответствует случаю полной устойчивости возрастания уровней. При полнойпротивоположности рангов уровней рангам лет коэффициент Спирмэна равен -1, что означаетполную устойчивость процесса сокращения уровней. При хаотическом чередовании ранговуровней коэффициент близок к нулю, это означает неустойчивость какой-либо тенденции.
Отрицательное значение rx указывает на наличие тенденции снижения уровней, причемустойчивость этой тенденции ниже средней.
При этом следует иметь в виду, что даже при 100%-ной устойчивости тенденции в рядудинамики может быть колеблемость уровней, и коэффициент их устойчивости будет ниже100%. При слабой колеблемости, но еще более слабой тенденции, напротив, возможен высокийкоэффициент устойчивости уровней, но близкий к нулю коэффициент устойчивости тренда. Вцелом же оба показателя связаны, конечно, прямой зависимостью: чаще всего большаяустойчивость уровней наблюдается одновременно с большей устойчивостью тренда.
37. Моделирование тенденции ряда динамики при наличии структурных изменений.
От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными факторами. В этом случае, начиная с некоторого момента времени t, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику.
Момент t сопровождается значительными изменениями ряда факторов, оказывающих сильное воздействие на изучаемый показатель Моделирование тенденции временного ряда при наличии структурных изменений.. Чаще всего эти изменения вызваны изменениями в общеэкономической ситуации или событиями глобального характера, приведшими к изменению структуры экономики. Если исследуемый временной ряд включает в себя соответствующий момент времени, то одной из задач его изучения становится выяснение вопроса о том, значительно ли повлияли общие структурные изменения на характер этой тенденции.
Если это влияние значимо, то для моделирования тенденции данного временного ряда следует использовать кусочно-линейные модели регрессии, т.е. разделить исходную совокупность на 2 подсовокупности (до момента времени t и после) и строить отдельно по каждой подсовокупности уравнения линейной регрессии.
Если структурные изменения незначительно повлияли на характер тенденции ряда Моделирование тенденции временного ряда при наличии структурных изменений., то ее можно писать с помощью единого для всей совокупности данных уравнения тренда.
Каждый из описанных выше подходов имеет свои положительные и отрицательные стороны. При построении кусочно-линейной модели снижается остаточная сумма квадратов по сравнению с единым для всей совокупности уравнением тренда. Но разделение совокупности на части ведет к потере числа наблюдений, и к снижению числа степеней свободы в каждом уравнении кусочно-линейной модели. Построение единого уравнения тренда позволяет сохранить число наблюдений исходной совокупности, но остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной моделью. Очевидно, что выбор модели зависит от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.
38. Регрессионный анализ связных динамических рядов.
Многомерные временные ряды, показывающие зависимость результативного признака от одного или нескольких факторных, называютсвязными рядами динамики. Применение методов наименьших квадратов для обработки рядов динамики не требует выдвижения никаких предположений о законах распределения исходных данных. Однако при использовании метода наименьших квадратов для обработки связных рядов следует учитывать наличие автокорреляции (авторегрессии), которая не учитывалась при обработке одномерных рядов динамики, поскольку ее наличие способствовало более плотному и четкому выявлению тенденции развития рассматриваемого социально – экономического явления во времени.
Выявление автокорреляции в уровнях ряда динамики
В рядах динамики экономических процессов между уровнями, особенно близко расположенными, существует взаимосвязь. Ее удобно представить в виде корреляционной зависимости между рядами y1,y2,y3,…..yn h y1+h, y2+h,…, yn+h. Временное смещение L называется сдвигом,а само явление взаимосвязи – автокорреляцией.
Автокорреляционная зависимость особенно существенна между последующими и предшествующими уровнями ряда динамики.
Различают два вида автокорреляции:
Автокорреляция в наблюдениях за одной или более переменными;
Автокорреляция ошибок или автокорреляция в отклонениях от тренда.
Наличие последней приводит к искажению величин средних квадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов регрессии, а так же проверку их значимости.
Автокорреляцию измеряют при помощи циклического коэффициента автокорреляции, который может рассчитываться не только между соседними уровнями, т.е. сдвинутыми на один период, но и между сдвинутыми на любое число единиц времени (L). Этот сдвиг, именуемыйвременным лагом, определяет и порядок коэффициентов автокорреляции: первого порядка (при L=1), второго порядка (при L=2) и т.д. Однако наибольший интерес для исследования представляет вычисление нециклического коэффициента (первого порядка), так как наиболее сильные искажения результатов анализа возникают при корреляции между исходными уровнями ряда и теми же уровнями, сдвинутыми на одну единицу времени.
Для суждения о наличии или отсутствия автокорреляции в исследуемом ряду фактическое значение коэффициентов автокорреляции сопоставляется с табличным (критическим) для 5% - го или 1% - го уровня значимости.
Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята. Когда же фактическое значение больше табличного, можно сделать вывод о наличии автокорреляции в ряду динамики.
Статистические расчеты содержания влаги
контрольная работа
2. Уравнение тренда на основе линейной зависимости.
2.1. Основные элементы временного ряда.
Можно построить эконометрическую модель, используя два типа исходных данных:
Данные, характеризующие совокупность различных объектов в определённый момент времени.
Данные, характеризующие один объект за ряд последовательных моментов времени.
Модели, построенные по данным первого типа, называются пространственными. Модели, построенные на основе второго типа данных, называются временными рядами.
Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
Факторы, формирующие тенденцию ряда.
Факторы, формирующие циклические колебания ряда.
Случайные факторы.
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы.
Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию. На рис. 1. показан временной ряд, содержащий возрастающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года. При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой бизнес цикла, в которой находится экономика страны. На рис. 2. представлен временной ряд, содержащий только сезонную компоненту.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень базируется как сумма среднего уровня ряда и некоторой случайной компоненты. Пример ряда, содержащего только случайную компоненту, приведён на рис. 3.
Очевидно, что реальные данные не следуют полностью из каких-либо описанных моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью.
2.2. Автокорреляция уровней временного ряда.
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией. Количественно её можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми во времени.
Одна из рабочих формул для расчёта коэффициента корреляции имеет вид:
r xy = (x j - x ) * (y j - y ) .
(x j -x) 2 * (y j -y) 2
В качестве переменной x мы рассмотрим ряд y 2 , y 3 , ... y t ; в качестве переменной y рассмотрим ряд y 1 , y 2 , ... y t -1 . Тогда данная формула примет вид:
r 1 = (y t - y 1 ) * (y t-1 - y 2 ) ; где y 1 = y t ; y 2 = y t-1 .
(y t -y 1) 2 * (y t-1 -y 2) 2 n - 1 n - 1
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка. Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Свойства коэффициента автокорреляции:
Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной тенденции.
Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда.
Последовательность коэффициентов автокорреляции уровней первого, второго, и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости её значений от величины лага называется коррелограммой. Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а, следовательно, и лаг, при котором связь между текущим и предыдущим уровнями ряда наиболее тесная, т.е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка t, ряд содержит циклические колебания с периодичностью в t моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать вывод: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.
2.3. Моделирование тенденции временного ряда.
Одним из наиболее распространённых способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.
Т.к. зависимость от времени может принимать разные формы, для её формализации можно использовать различные виды функции. Для построения трендов чаще всего применяются следующие функции:
Линейный тренд: y t = a + b*t ;
Гипербола:y t = a + b/t ;
Экспоненциальный тренд: y t = e a + b * t ;
Тренд в форме степенной функции: y t = a*t ;
Парабола: y t = a + b 1 *t + b 2 *t 2 + ... + b k *t k ;
Параметры каждого из этих трендов можно определить методом наименьших квадратов, используя в качестве независимой переменной время t = 1, 2, ... ,n , а в качестве зависимой переменной - фактические уровни временного ряда y t . Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Существует несколько способов определения типа тенденции. К числу наиболее распространённых способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчёт некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляция первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни y t и y t -1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит не6линейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации R и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации.
Высокие значения коэффициентов автокорреляции первого, второго и третьего порядков свидетельствуют о том, что ряд содержит тенденцию. Приблизительно равные значения коэффициентов автокорреляции по уровням этого ряда и по логарифмам уровней позволяют сделать следующий вывод: если ряд содержит нелинейную тенденцию, то она выражена в неявной форме. Поэтому для моделирования его тенденции в равной мере целесообразно использовать и линейную, и нелинейную функции, например степенной или экспоненциальный тренд. Для выявления наилучшего уравнения тренда необходимо определить параметры основных видов трендов.
Наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов. Параметры линейного тренда:
a - начальный уровень временного ряда в момент времени t = 0;
b - средний за период абсолютный прирост уровней ряда.
Расчётные по линейному тренду значения уровней временного ряда определяются двумя способами. Во-первых, можно последовательно подставлять в найденное уравнение тренда значения t = 1, 2, ..., n. Во-вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста.
Задача №1
Десять человек различного возраста имеют следующие параметры:
1. Определить результативный признак.
Рассчитаем зависимость роста от возраста:
Фактор (X): возраст.
Результативный признак (Y): рост.
a*x + b*x 2 = x*y
10*a + 248*b = 1812
248*a + 6492*b = 45023
a = 1812 - 248*b => 1812 - 248*b *248 + 6492*b = 45023
r = x*y - ( x* y)/n = 45023 - (248*1812)/10 =>
(x 2 - (x) 2 /n)*(y 2 - (y) 2 /n) (6492 - 248 2 /10)*(328444 - 1812 2 /10)
r = 0.44 - прямая умеренная связь
r 2 = 0.19 - рост на 19% зависит от возраста
Тест Фишера:
F cp = r 2 * (n - 2)
F cp = 0.19 * (10 - 2) = 1.78
F табл = 5.32
F cp < F табл =>
Рассчитаем зависимость веса от возраста:
Фактор (X): возраст.
Определим параметры линейной функции с помощью системы уравнений:
a*x + b*x 2 = x*y
10*a + 248*b = 753
248*a + 6492*b = 18856
a = 753 - 248*b => 1812 - 248*b *248 + 6492*b = 18856
r = x*y - ( x* y)/n = 18856 - (248*753)/10 =>
(x 2 - (x) 2 /n)*(y 2 - (y) 2 /n) (6492 - 248 2 /10)*(56967 - 753 2 /10)
r = 0.6 - заметная прямая связь
r 2 = 0.36 - вес на 36% зависит от возраста
Тест Фишера:
F cp = r 2 * (n - 2)
F cp = 0.36 * (10 - 2) = 4.5
F табл = 5.32
F cp < F табл => нулевая гипотеза подтвердилась, уравнение статистически незначимо.
Рассчитаем зависимость веса от роста:
Фактор (X): рост.
Результативный признак (Y): вес.
Определим параметры линейной функции с помощью системы уравнений:
a*x + b*x 2 = x*y
10*a + 1812*b = 753
1812*a + 328444*b = 136562
a = 753 - 1812*b => 753 - 1812*b *1812 + 328444*b = 136562
r = x*y - ( x* y)/n = 136562 - (1812*753)/10 =>
(x 2 - (x) 2 /n)*(y 2 - (y) 2 /n) (328444 - 1812 2 /10)*(56967 - 753 2 /10)
r = 0.69 - заметная прямая связь
r 2 = 0.47 - вес на 47% зависит от роста
x = 1812/10 = 181.2
Тест Фишера:
F cp = r 2 * (n - 2)
F cp = 0.47 * (10 - 2) = 7.1
F табл = 5.32
F cp > F табл => нулевая гипотеза не подтвердилась, уравнение имеет экономический смысл.
Тест Стьюдента:
Рассчитаем случайные ошибки:
.
m a = (y - y x ) 2 * x 2 .
n - 2 n*(x -x) 2
m b = (y - y x ) 2 / (n - 2)
m r = 1 - r 2
m a = 138.19 * 328444 = 72
m b = 138.19 / (10 - 2) = 1
m r = 1 - 0.47 = 0.26
t a = a/m a = 120/72 = 1.67
t b = b/m b = 1.08/1 = 1.08
t r = r/m r = 0.69/0.26 = 2.65
t табл = 2.3
Для расчёта доверительного интервала рассчитаем предельную ошибку:
a = t табл - t a = 2.3 - 1.67 = 0.63
b = t табл - t b = 2.3 - 1.08 = 1.22
r = t табл - t r = 2.3 - 2.65 = -0.35
Рассчитаем доверительные интервалы:
a = a a = -121.03 119.77
b = b b = -0.14 2.3
r = r r = 0.34 1.04
Задача №2
При контрольной выборочной проверке процента влажности почвы фермерских хозяйств региона получены следующие данные:
1. С вероятностью 0.95 и 0.99 установить предел, в котором находится средний процент содержания влаги.
2. Сделать выводы.
Генеральная средняя: x = x = 31.1 = 3.8875
Генеральная дисперсия: 2 = (x - x ) 2 = 1.8875 = 0.1261
n 8 .
Средняя квадратическая стандартная ошибка: x = 2 = 0.1261 = 0.126
Предельная ошибка выборки: x = t* x
Из таблицы значений t-критерия Стьюдента:
Для вероятности 0.95, предельная ошибка выборки:
x = 2.4469*0.126 = 0.308
Для вероятности 0.99, предельная ошибка выборки:
x = 3.7074*0.126 = 0.467
Доверительные интервалы:
Предел среднего процента содержания влаги с вероятностью 0.95:
Верхний центральный показатель некоторой линейной системы
Пусть дана система (2) и - ее решение. Рассмотрим семейство функций, Определение 5 : Функция R (t) называется верхней для системы (2), если она ограничена, измерима и осуществляет оценку, Где - норма матрицы Коши линейной системы...
Дифференциальное исчисление
Исходя из определения производной сформулируем следующее правило нахождения производной функции в точке: Чтобы вычислить производную функции f(x) в точке x0 нужно: 1) Найти f(x) - f(x0); 2) составить разностное отношение; 3) вычислить предел...
Дифференциальное исчисление
Исходя из определения производной...
Инвариантные подгруппы бипримарных групп
В заметке (1) исправлена ошибка, допущенная Бернсайдом в работе (2). А именно в (3) доказано, что группа порядка, где и - различные простые числа и, либо обладает характеристической -подгруппой порядка...
Использование современной компьютерной техники и программного обеспечения для решения прикладной задачи из инженерно-буровой практики
Зная значения коэффициентов а0, а1 и а2 можно найти значений y` по формуле, в нашем случае. Различие между экспериментальными и теоретическими данными невелико. Полученные данные позволяет нам найти зависимость, 5...
Линейная сложность циклотомических последовательностей
Пусть последовательность четвертого порядка, то есть, тогда, согласно лемме 1.1, она формируется по правилу: (2.1) Заметим, что правило (2.1) задает последовательность только тогда, когда...
Математическая модель цифрового устройства игры "Крестики-нолики" с человеком
Игровое поле игры в крестики-нолики может быть представлено в виде сетки, состоящей из строк и столбцов. Каждый элемент сетки может находиться в трех состояниях: пустое (начальное), отмечено крестиком, отмечено ноликом...
Методы отсечения
Среди совокупности п неделимых предметов, каждый i-и (i=1,2,…, п) из которых обладает по i-й характеристике показателем и полезностью найти такой набор, который позволяет максимизировать эффективность использования ресурсов величины...
Приближенное решение алгебраических и трансцендентных уравнений. Метод Ньютона
Информация о предыдущих приближениях корня используется для нахождения последующих приближений не только в методе касательных. В качестве примера другого такого метода мы приведём метод...
Статистические расчеты содержания влаги
Практические задачи: 1. Десять человек различного возраста имеют следующие параметры: Возраст, лет 18 20 21 22 22 24 25 26 31 39 Рост, см 174 183 182 180 178 179 185 185 184 182 Вес, кг 65 73 69 74 77 75 78 84 79 79 1...
