Пусть на задана непрерывная функция f(x). Введем сетку
и обозначим f i =f(x i ), i=0,1,N .
Сплайном, соответствующим данной функции f(x) и данным узлам , называется функция S(x), удовлетворяющая следующим условиям:
1. На каждом сегменте , i=1,2,N , функция S(x) является многочленом третьей степени;
2. Функция S(x),
а также ее первая и вторая производные
непрерывны на ;
Последнее условие называется условием интерполирования , а сплайн, определяемый условиями 1)-3), называется также интерполяционным кубическим сплайном.
Докажем существование и единственность сплайна, определяемого перечисленными условиями. Приведенное ниже доказательство содержит также способ построения сплайна.
В промежутке между парой соседних узлов интерполяционная функция является многочленом 3-ей степени, который удобно записать в виде:
Коэффициенты многочлена определяют из условий в узлах. Он должен принимать табличные значения:
 (1)
(1)
Число уравнений в два раза меньше числа неизвестных коэффициентов, поэтому для замыкания нужны дополнительные условия. Найдем первую и вторую производные от кубического многочлена:
 (2)
(2)
Потребуем непрерывности этих производных (т. е. гладкости гибкой линейки) во всех точках, включая узлы. Приравнивая во внутреннем узле х i правые и левые пределы производных получаем:
 3)
3)
Недостающие два условия обычно получают из естественного предположения о нулевой кривизне графика на концах:
что соответствует свободно опущенным концам линейки. Но если есть дополнительные сведения об асимптотике функции, то можно записать другие краевые условия.
Уравнения (1-4) образуют систему линейных уравнений для определения 4N неизвестных коэффициентов. Эту систему можно решить методом исключения Гаусса, но выгоднее привести ее к специальному виду.
Уравнение (1) дает сразу все коэффициенты а i . Из уравнений (3) и (4)
 (5)
(5)
Подставим (5) в (1), одновременно исключая а i = f i -1 , получим:
 (6)
(6)
Исключая теперь из (3) b i и b i +1 по (6) и d i по (5), получаем систему уравнений для с i:

Матрица этой системы 3-х диагональная. Такие системы экономно решаются методом прогонки.
В силу диагонального преобладания система имеет единственное решение.
После нахождения с i определяются a i , b i и d i и определяется вид кубических многочленов (сплайнов) на каждом отрезке.
Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями 1)-3) и граничными условиями
Заметим, что можно рассматривать и другие граничные условия.
Можно рассмотреть и более общую задачу интерполяции функции сплайном – многочленом n-ой степени
![]() ,
,
коэффициенты которого кусочно - постоянны, и который в узлах принимает заданные значения и непрерывен вместе со своими (n-1) производными.
На практике наиболее употребительны 2 случая: один при n=3 (кубические многочлены) уже рассмотрен, второй при n-1 (многочлены Ньютона 1-ой степени) соответствует аппроксимации графика ломаной, построенной по узлам; определение коэффициентов при этом очевидно.
ЛЕКЦИЯ №14
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

ПРОСТЫЕ КВАДРАТУРНЫЕ ФОРМУЛЫ
Общая формула прямоугольников
![]()

1. Квадратурная формула левых прямоугольников.
![]()
2. Формула правых прямоугольников
3. Квадратурная формула средних прямоугольников

Расчет погрешности формул численного интегрирования.
Пусть h>0 достаточно мало, x 0 =0.
Разложим функцию в ряд Тейлора в окрестности x 0 =0. :


Локальная погрешность для малого отрезка h -
 , то есть
, то есть


Свойство аддитивности
![]()
 - погрешность на отрезке .
- погрешность на отрезке .
Квадратурные формулы Ньютона-Котеса
![]()
Если многочлен n - степени, то
Это квадратурные формулы интерполяционного типа. Здесь С к – коэффициенты Котеса
Безразмерные формулы.



![]()

В промышленном производстве, например, судо-, автомобиле- и авиастроении, окончательная форма в реальном или близком к нему масштабе определяется в процессе доводки.
Автоматизация этого процесса представляла значительный интерес для машинной графики. Форма математического сплайна повторяет контур физического сплайна (рис. 5-4), т.е. гибкой деревянной или пластмассовой линейки, проходящей через определенные точки. Для изменения формы сплайна используются свинцовые грузики. Меняя их количество и расположение, получившуюся кривую стараются сделать более гладкой, красивой и «приятной для глаза».
Если рассматривать физический сплайн как тонкую гибкую рейку, его форма (отклонение ) определяется уравнением Эйлера (5-2) для момента изгиба вдоль рейки:
где - модуль Юнга, зависящий от свойств материала рейки, - момент инерции, определяемый формой кривой, - радиус кривизны.
Для малых отклонений радиус приближенно равен
 ,
,
где штрих обозначает производную по - расстоянию вдоль рейки, а - отклонение рейки. Уравнение Эйлера принимает вид
Пусть грузики действуют как
простые подпорки, тогда момент изгиба между ними изменяется линейно. Подставляя
![]() в
уравнение Эйлера, получаем
в
уравнение Эйлера, получаем
и после двойного интегрирования
Таким образом, форма сплайна задается кубическим полиномом.
В общем случае математический сплайн это кусочный полином степени с непрерывной производной степени в точках соединения сегментов. Так, например, кубический сплайн имеет в точках соединения непрерывность второго порядка. Кусочные сплайны из многочленов невысокого порядка очень удобны для интерполяции кривых, так как они не требуют больших вычислительных затрат и не вызывают численных отклонений, свойственных многочленам высокого порядка. По аналогии с физическими сплайнами обычно используется серия кубических сегментов, причем каждый сегмент проходит через две точки. Кубический сплайн удобен еще и тем, что это кривая наименьшего порядка, допускающая точки перегиба и изгиб в пространстве.
Уравнение одного параметрического сегмента сплайна таково:
 ,
, (5-1)
,
, (5-1)
где
и - значения
параметров в начале и конце сегмента. - вектор к любой точке сегмента. ![]() - это
векторно-значная функция, где три составляющие - декартовы координаты вектора.
- это
векторно-значная функция, где три составляющие - декартовы координаты вектора.

Рис. 5-5 Один сегмент кубического сплайна.
Каждая составляющая имеет вид, похожий на , т.е.
 ,
,
,
,
 ,
,
,
,
 ,
.
,
.
Постоянные коэффициенты вычисляются исходя из четырех граничных условий для сегмента сплайна. Запишем уравнение (5-1) в виде
Пусть и - векторы концов сегмента (см. рис. 5-5). Пусть также и , производные по , будут касательными векторами в концах сегмента. Дифференцируя уравнение (5-1), получим
 , . (5-3)
, . (5-3)
Запишем результат
![]() , . (5-4)
, . (5-4)
Предположим, без потери общности, что , и применим граничные условия
Получим четыре уравнения для неизвестных :
 , (5-6b)
, (5-6b)
 , (5-6c)
, (5-6c)
 . (5-6d)
. (5-6d)
Решения для и имеют вид:
 (5-7a)
(5-7a)
 . (5-7b)
. (5-7b)
Величины , , и задают сегмент кубического сплайна. Очевидно, что форма сегмента зависит от положения и касательных векторов в концах сегмента. Далее, заметим, что в результатах присутствует значение параметра в конце сегмента. Так как каждая конечная точка и вектор касания имеют три компоненты, параметрическое уравнение кубической пространственной кривой зависит от двенадцати векторных компонент и значения параметра в конце сегмента.
Подставив уравнения (5-6) и (5-7) в (5-1), получим уравнение для одного сегмента кубического сплайна:

 . (5-8)
. (5-8)
Это уравнение для одного сегмента. Чтобы получить кривую целиком, нужно соединить множество сегментов. На рис. 5-6 показаны два соседних сегмента. Если известны векторы , , , касательные векторы , , и значения параметров , , то форма каждого сегмента определяется из уравнения (5-8). Однако маловероятно, что известен касательный вектор в точке соединения. К счастью, его можно вывести из условия непрерывности.
Вспомним, что кусочный сплайн степени имеет непрерывность степени в точках соединения; непрерывность кубического сплайна равна двум. Для этого должна быть непрерывна вторая производная или кривизна линии. Дважды продифференцировав уравнение (5-1), получим
 , . (5-9)
, . (5-9)

Рис. 5-6 Два кусочно кубических сегмента сплайна.
Для первого куска сплайна параметр изменяется в пределах . Подставим в уравнение (5-9):
![]() .
.
Для второго участка сплайна параметр изменяется в диапазоне . Подставим в уравнение (5-9) значение в начале второго участка
Приравнивая полученные результаты и пользуясь уравнениями (5-6a,b) и (5-7а), получим
 .
.
Левая часть этого уравнения представляет кривизну в конце первого сегмента, а правая - в начале второго. Домножим на и сгруппируем члены:
Отсюда определяется , неизвестный касательный вектор в точке соединения. Отметим, что в окончательном уравнении опять присутствуют значения параметра в концах сегментов и .
Полученную формулу можно обобщить для точек, и для сегментов кубического сплайна получить непрерывность второго порядка в точках соединения.

Рис. 5-7 Обозначения множества кусочно кубических сегментов сплайна.
Обобщенное уравнение для двух любых соседних сегментов сплайна и в обозначениях рис. 5-7 имеет вид:

 (5-11)
(5-11)
для первого сегмента и
 (5-12)
(5-12)
для второго, так как для каждого сегмента параметр начинает изменяться с нуля, для первого и для второго - .
Приравнивание вторых производных
в точках стыковки для любых соседних сегментов, ![]() , дает общий результат, эквивалентный
уравнению (5-10),
, дает общий результат, эквивалентный
уравнению (5-10),
откуда определяется касательный вектор в точках соединения любых двух сегментов и .
Рекурсивное использование уравнения (5-13) для всех сегментов сплайна порождает уравнений касательных векторов , . В матричной форме:

 (5-14)
(5-14)
Матрица неквадратная, так как имеется только уравнений для векторов, и ее нельзя обратить и получить решение для . Если предположить, что известны касательные векторы на концах кривой и , проблема разрешается. Теперь матрица имеет вид

 (5-15)
(5-15)
где матрица квадратная и обратимая. Заметим также, что трехдиагональная, что снижает вычислительные затраты на ее обращение. Далее, матрица диагонально доминантная. Отсюда следует, что у нее существует единственное решение:
![]() . (5-16)
. (5-16)
Если нам известны , то легко определить коэффициенты для каждого сегмента сплайна. Обобщая уравнения (5-6)-(5-11), получим
 ,
,
 .
.
Так как и - это векторные величины, то и тоже векторные; если и имеют , составляющие, значит, и также имеет эти составляющие.
В матричной форме уравнение любого сегмента сплайна таково:
 . (5-17)
. (5-17)
Пусть требуется задать кубический сплайн, проходящий через точек , с касательными векторами на концах и . Из уравнения (5-16) находим внутренние касательные векторы , . Затем из уравнения (5-17) с известными координатами концов каждого сегмента и касательными векторами определяются , , для каждого сегмента. Окончательное обобщение уравнения (5-1)
 ,
, , (5-18)
,
, , (5-18)
используется для расчета сегмента сплайна.
В матричном виде уравнение (5-18) выглядит следующим образом:
 ,
. (5-19)
,
. (5-19)
Подставляя уравнение (5-17) и перегруппируя члены, получим
 , , , (5-20)
, , , (5-20)
![]() , (5-21a)
, (5-21a)
![]() , (5-21b)
, (5-21b)
![]() , (5-21с)
, (5-21с)
![]() , (5-21d)
, (5-21d)
называются весовыми функциями.

Рис. 5-8 Весовые функции кубического сплайна для
Пользуясь этими определениями, запишем уравнение (5-20) в матричном виде
где - матрица весовой функции
содержит геометрическую информацию. Как будет видно из дальнейшего, уравнения типа (5-22), т.е. матрица весовой функции, умноженная на матрицу геометрических условий, часто применяются для описания кривых и поверхностей.
Из уравнения (5-21) видно, что
каждая весовая функция имеет третий порядок. Любая точка на сегменте
кубического сплайна это взвешенная сумма конечных точек и касательных векторов.
Коэффициенты выступают
в роли весовых функций. На рис. 5-8 изображены для . Из рисунка видно, что и , т.е. кривая
проходит через вектор-точку . Аналогично и , т.е. кривая также проходит
через вектор-точку .
Далее отметим симметрию и , и и . Фактически ![]() . Наконец, обратим внимание на
относительный порядок , , и . Значительная разница величин говорит о
том, что в общем случае положение конечных точек имеет большее влияние, чем
касательные векторы.
. Наконец, обратим внимание на
относительный порядок , , и . Значительная разница величин говорит о
том, что в общем случае положение конечных точек имеет большее влияние, чем
касательные векторы.
Вспомним, что кусочный кубический сплайн определяется точками, векторами касательных и величинами параметра, т. е. в концах всех сегментов. Выбор влияет на гладкость кривой.
Непрерывность второй производной в точках внутреннего соединения сама по себе не обеспечивает гладкости кривой в смысле минимальности кривизны вдоль нее. Подбирая соответствующие значения, можно минимизировать коэффициенты и для каждого сегмента и достичь большей гладкости кривой. Обычно эти дополнительные вычисления не требуются. Для практических целей применяются более простые методы, наподобие рассмотренных здесь.
Один метод вычисления - установить величины параметров равными длинам хорд между соседними точками. При этом качество кривой удовлетворяет требованиям большинства прикладных задач. Другой метод состоит в том, что для нормализации вариации полагается равным единице у каждого сегмента сплайна. Такой выбор упрощает вычисления (см. разд. 5-4). Как видно из приведенных выше уравнений, любой выбор приводит к другим коэффициентам, и, следовательно, получаются различные кривые, проходящие через заданные точки.
Рассмотрим пример.
|
Пример 5-2 Кубический сплайн Пусть даны четыре вектор-точки на плоскости: , , , (см. рис. 5-9). Найти кусочный кубический сплайн, проходящий через них, используя хордовую аппроксимацию . Касательные векторы в концах: и . Найти промежуточные точки при для каждого сегмента. Сначала найдем Внутренние касательные векторы и вычисляются из уравнения (5-15):
Рис. 5-9 Кусочный кубический сплайн. (а) вычислены с помощью хордовой аппроксимации; (b) нормализованы к 1. Сделав подстановку, получим
С помощью инверсии и умножения вычисляются касательные векторы
|
|||
|
То кривая выпукла на концах и лежит внутри треугольника из хорды и касательных. При возрастании величины кривая постепенно становится вогнутой и выходит за треугольник. В этом случае при величине вектора у кривой появляется вершина (см. рис. 5-10d). При еще больших величинах появляется петля, как видно из рис. 5-10е. Иногда для улучшения формы кривой величина вектора ограничивается длиной хорды. |
И уже почти год с того момента, как пришла в голову идея для второй. В силу многих обстоятельств (в первую очередь – лени и забывчивости), эта идея так и не была реализована ранее, но сейчас я собрался, написал весь этот материал и готов представить его вашему вниманию.
Начну с небольшой вводной. Будучи студентом 4-го, на тот момент, курса бакалавриата, я изучал курс «Компьютерная графика». Много там было разных интересных (и не очень) заданий, но одно прямо особо запало мне в душу: интерполяция кубическими сплайнами с заданными первыми производными на концах интервала. Пользователь должен был задавать значения первых производных, а программа - считать и выводить на экран интерполяционную кривую. Особенность и основная сложность задания заключена в том, что задаются именно первые производные, а не вторые, как в классической постановке сплайн-интерполяции.
Как я ее решал, и к чему оно в итоге пришло, я как раз и изложу в этой статье. И да, если по описанию задачи вы не поняли ни в чем ее смысл, ни в чем сложность, не переживайте, все это я также постараюсь раскрыть. Итак, поехали.
А, нет, погодите один момент. Вот вам два числовых ряда:
a) 2, 4, 6, 8, ?
b) 1, 3, ?
, 7, 9
Какие числа должны стоять на месте вопросов и почему? Вы действительно уверены в своем ответе?
Интерполяция
Интерполяция, интерполирование (от лат. inter-polis – «разглаженный, подновлённый, обновлённый; преобразованный») – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. (с) Википедия
Поясню на примерах. Существуют задачи, когда нам требуется узнать, условно, «закон распределения» (взял в кавычки, так как это, вообще говоря, термин из другой области математики) некого параметра по нескольким известным его значениям. Чаще всего речь идет об изменении некого параметра во времени: координаты движущегося тела, температуры объекта, колебания курса валюты, etc. При этом в силу каких-либо обстоятельств у нас не было возможности наблюдать за этим параметром непрерывно, мы могли узнавать его значения лишь в какие-то отдельные моменты времени. Исходными данными в таком случае у нас является множество точек вида value(time) , а целью задачи – восстановить кривую, проходящую через эти точки и непрерывно описывающую изменение этого параметра.
Следует понимать, что невозможность постоянного наблюдения за соответствующим параметром – это обычно какого-либо рода технологическое ограничение. С развитием техники таких ситуаций становится все меньше и меньше. Из современных задач такого плана – траектория движения, например, марсохода. Поддерживать непрерывный сеанс связи (пока что) все еще не представляется возможным, а контролировать его перемещение и рисовать красивые траектории хочется. Получается, что конкретные координаты можно узнать только в те моменты, когда связь все-таки налажена, а траекторию целиком приходится восстанавливать по полученным таким образом время от времени точкам.
Другой вариант применения интерполяции. Некоторые современные телевизоры показывают изображение с частотой обновления картинки до >=1000Гц (хотя это все еще запредельные значения). Большинство телевизоров так не умеет, но даже так многие отображают картинку на частоте 100Гц - такая величина уже вполне себе классика. А если верить википедии, то в кинематографе «частота 24 кадра в секунду является общемировым стандартом». Для того, чтобы превратить 24 кадра в секунду исходного видеопотока в 100 кадров в секунду результата, телевизор использует интерполяцию. А именно какие-нибудь алгоритмы в стиле «взять два соседних кадра 1 и 2, посчитать разницу между ними и сформировать из нее 3 дополнительных кадра, которые надо впихнуть между теми двумя изначальными» -> получаются кадры 1, 1_1
, 1_2
, 1_3
, 2
Для дальнейших рассуждений возьмем более простой пример. Представим себе, например, лабораторную работу по географии в каком-нибудь 6-ом классе (кстати, у меня когда-то и правда была такая). Необходимо каждые 3 часа измерять температуру воздуха и записывать данные, а потом сдать учителю график изменения температуры от времени суток. Допустим, по результатам измерений у нас получилась вот такая табличка (данные придуманы случайным образом и никак не претендуют на какую-либо правдоподобность):
Отобразим полученные данные на графике:

Собственно, данные записаны и отражены на графике. Мы вплотную подошли к задаче интерполяции – как по имеющимся точкам восстановить плавную кривую?
Количество условий и степень интерполирующего полинома
Можем ли мы вообще гарантировать, что такая функция, которая соединяет все заданные точки, вообще существует?Да, такая функция гарантированно существует, и более того, таких функций будет бесконечно много. Для любого набора точек можно будет придумать сколько угодно много функций, которые через них будут проходить. И вот несколько примеров того, как две точки можно соединить разными способами:



Однако есть и способ задать интерполяционную кривую однозначно. В самом классическом случае, в качестве интерполяционной кривой берут полином:
Для того, чтобы провести через имеющиеся точки такой полином единственным образом, необходимо и достаточно, чтобы степень полинома была на 1 меньше, чем количество условий (я специально выделил это слово, потому что в конце этого раздела я вернусь к этой формулировке). Пока что, простоты ради, условием будут являться координаты точки. Говоря человеческим языком, через 2 точки однозначным образом можно провести прямую (полином 1-ой степени), через 3 точки – параболу (полином 2-ой степени) и т.д.
Возвращаясь к нашей задаче с температурой – в ней мы определили 6 точек, значит, для того, чтобы провести полином единственным образом, он должен быть 5-ой степени

Интерполирующий полином тогда будет выглядеть так:
$inline$-\frac{x^5}{14580}+\frac{13x^4}{1944}-\frac{41x^3}{162}+\frac{983x^2}{216}-\frac{2273x}{60}+117$inline$
А сейчас следует сделать важное замечание и пояснить, что я имел ввиду под «условием»
. Полином можно задать не только координатами точек, через которые он проходит, условиями могут быть любые параметры этого полинома. В простейшем случае это действительно координаты точек. Но в качестве условия можно взять, например, первую производную этого полинома в какой-либо из точек. Вторую производную. Третью производную. В общем, любую возможную производную в любой из точек, в которой этот полином существует. Поясню на примере:
Прямую можно задать однозначно, как я уже говорил, двумя точками:

Ту же прямую, с другой стороны, можно определить координатой одной точки и углом наклона альфа к горизонтали:

С полиномами более высоких степеней можно использовать и более сложные условия (вторая производная, третья производная, etc.), и каждый такой параметр будет идти в общий счет количества условий, которые однозначным образом определят этот полином. Чтобы не быть голословным, вот еще пример:
Пусть нам заданы такие три условия:
Условий три, значит, мы хотим получить полином второй степени:
Подставляем
Считаем первую производную и считаем
Считаем вторую производную и считаем
Отсюда получаем, что наш полином выглядит так:
Интерполяция кубическими сплайнами
Вот, по тиху, мы и подбираемся к моей задаче. Полиномиальная интерполяция – не единственно возможный способ интерполяции. Среди всех прочих методов существует метод интерполяции кубическими сплайнами.Принципиальное отличие идеи сплайн-интерполяции от интерполяции полиномом состоит в том, что полином один, а сплайн состоит из нескольких полиномов, а именно их количество равно количеству инервалов, внутри которых мы производим интерполяцию. В примере с нашей температурой воздуха, в которой у нас определено 6 точек, у нас будет 5 интервалов – соответственно, у нас будут 5 полиномов, каждый на своем интервале.
Каждый из этих полиномов – это полином третьей степени (строго говоря, степени не выше третьей, так как на каком-то из интервалов интерполирующая кривая может становиться квадратичной параболой или даже линейной функцией, но в общем случае это все-таки полином именно третьей степени). Записывая вышесказанное формульно, получим что все наши точки будут соединены некоей кривой , где каждый – это полином третьей степени, а именно:
Возвращаясь к рассказанному в предыдущем пункте, для того, чтобы однозначно задать один полином 3-ей степени, необходимо 4 условия. В этой задаче у нас 5 полиномов, то есть, чтобы задать их все, нам нужно суммарно 5∙4=20 условий. И вот как они получаются:
1) Первый полином определен на первой и второй точках – это два условия. Второй полином определен на второй и третьей точках – еще два условия. Третий полином, четвертый, пятый – каждый из них определен на 2-х точках – суммарно это дает 10 условий.
2) Для каждой промежуточной точки из множества (а это 4 точки с временами 12:00, 15:00, 18:00, 21:00) должно выполняться условие, что первые и вторые производные для левого и правого полиномов должны совпадать. Формульно:
По два таких условия на каждую из промежуточных точек дает еще 8 условий. Следует добавить, что мы задаем только сам факт равенства, а какое конкретно значение они при этом принимают – это совершенно иная задача и считается она довольно сложно.
3) Остаются два условия, которые пока еще не определены. Это так называемые «граничные условия», от задания которых и зависит, какой именно сплайн получится. Обычно задают вторые производные на концах интервала равными 0:
Если сделать так, то мы получим так называемый «естественный сплайн». Для вычисления таких сплайнов написано уже огромное количество библиотек, бери и используй любую.
Отличие моего задания от классической постановки задачи, мои размышления над заданием и само решение
И вот мы подошли к условию моей задачи. Преподаватель придумал такое задание, что задаваться должны первые производные и на левом и правом концах интервала, а программа должна считать интерполирующую кривую. А для такого требования готовых алгоритмов я не нашел…Я, разумеется, не стану описывать весь твой «творческий» путь от момента, когда я услышал задание, до того, как я его сдал. Расскажу лишь саму идею и покажу ее реализацию.
Сложность задания состоит в том, что, задавая первые производные на концах интервала, да, мы задаем этот сплайн. Теоретически. А вот посчитать его на практике – задача довольно сложная и совершенно неочевидная (желающие могут посмотреть код нахождения естественного сплайна на Вики – ru.wikipedia.org/wiki/Кубический_сплайн – и попробовать его понять хотя бы). Разумеется, я совершенно не хотел провести кучу времени, закопавшись в матан и пытаясь вывести нужные мне формулы. Я хотел более простое и элегантное решение. И я его нашел.
Рассмотрим наш сплайн и возьмем первый из его интервалов. На этом интервале уже заданы 3 условия:
Задается пользователем
Для того, чтобы однозначно задать кубический полином на этом интервале, нам не хватает еще лишь одного условия. Но мы можем его просто придумать! Возьмем вторую производную и положим ее равной, например, 0:
Ничем не обоснованное предположение
Таким образом, зная эти 4 условия, мы полностью определяем этот полином. Зная все параметры этого полинома, мы можем вычислить значения первой и второй производных на второй точке, и поскольку они совпадают со значениями первой и второй производной для полинома на втором интервале, это приводит к тому, что мы также определяем и второй полином:
Вычисляется из
Вычисляется из
Аналогично мы считаем третий полином, четвертый, пятый и так далее, сколько бы их ни было. То есть, по факту, воссоздаем весь сплайн. Но поскольку мы взяли совершенно случайным образом, это приведет к тому, что производная , заданная пользователем на правом конце сплайна, не будет совпадать с производной , которая получилась у нас в ходе таких вычислений. Но получается, что значение производной на правом конце сплайна – это функция, зависящая от значения второй производной на левом конце:
А поскольку такой сплайн, который бы удовлетворял заданным условиям, гарантированно существует, и существует в единственном экземпляре, это значит, что мы можем рассмотреть разность:
И попытаться найти такое значение , при котором обращалась бы в 0 – и это будет тем самым правильным значением , которое строит искомый пользователем сплайн:

Самое замечательное в моей идее то, что эта зависимость оказалась линейной (вне зависимости от количества точек, через которые мы проводим сплайн. Этот факт доказан теоретическими подсчетами), а значит можно случайным образом взять любые два начальные значения и , посчитать и , и сразу же посчитать то самое верное значение, которое построит нам искомый сплайн:
Итого, мы гарантированно находим искомый сплайн за 3 прогонки таких вычислений.
Немного кода и скриншотов программы
class CPoint { public int X { get; } public int Y { get; } public double Df { get; set; } public double Ddf { get; set; } public CPoint(int x, int y) { X = x; Y = y; } }Class CSplineSubinterval { public double A { get; } public double B { get; } public double C { get; } public double D { get; } private readonly CPoint _p1; private readonly CPoint _p2; public CSplineSubinterval(CPoint p1, CPoint p2, double df, double ddf) { _p1 = p1; _p2 = p2; B = ddf; C = df; D = p1.Y; A = (_p2.Y - B * Math.Pow(_p2.X - _p1.X, 2) - C * (_p2.X - _p1.X) - D) / Math.Pow(_p2.X - _p1.X, 3); } public double F(int x) { return A * Math.Pow(x - _p1.X, 3) + B * Math.Pow(x - _p1.X, 2) + C * (x - _p1.X) + D; } public double Df(int x) { return 3 * A * Math.Pow(x - _p1.X, 2) + 2 * B * (x - _p1.X) + C; } public double Ddf(int x) { return 6 * A * (x - _p1.X) + 2 * B; } }
Class CSpline { private readonly CPoint _points; private readonly CSplineSubinterval _splines; public double Df1 { get { return _points.Df; } set { _points.Df = value; } } public double Ddf1 { get { return _points.Ddf; } set { _points.Ddf = value; } } public double Dfn { get { return _points[_points.Length - 1].Df; } set { _points[_points.Length - 1].Df = value; } } public double Ddfn { get { return _points[_points.Length - 1].Ddf; } set { _points[_points.Length - 1].Ddf = value; } } public CSpline(CPoint points) { _points = points; _splines = new CSplineSubinterval; } public void GenerateSplines() { const double x1 = 0; var y1 = BuildSplines(x1); const double x2 = 10; var y2 = BuildSplines(x2); _points.Ddf = -y1 * (x2 - x1) / (y2 - y1); BuildSplines(_points.Ddf); _points[_points.Length - 1].Ddf = _splines[_splines.Length - 1].Ddf(_points[_points.Length - 1].X); } private double BuildSplines(double ddf1) { double df = _points.Df, ddf = ddf1; for (var i = 0; i < _splines.Length; i++) { _splines[i] = new CSplineSubinterval(_points[i], _points, df, ddf); df = _splines[i].Df(_points.X); ddf = _splines[i].Ddf(_points.X); if (i < _splines.Length - 1) { _points.Df = df; _points.Ddf = ddf; } } return df - Dfn; } }



Синие отрезки - это первые производные сплайна в соответствующих его точках. Добавил такой вот графический элемент для большей наглядности.
Достоинства и недостатки алгоритма
Признаюсь честно, я не проводил сколь-либо серьезного анализа. По-хорошему стоило бы написать тесты, проверить, как оно работает в разных условиях (мало/много точек интерполяции, равное/произвольное между точками, линейные/квадратные/кубические/тригонометрические/etc. функции и так далее), но я этого не сделал, простите:)Навскидку можно сказать, что сложность алгоритма - O(N), так как, как я уже говорил, вне зависимости от количества точек, достаточно двух прогонов вычислений, чтобы получить правильное значение второй производной на левом конце интервала, и еще одного, чтобы построить сплайн.
Впрочем, если кому-то захочется покопаться в коде и провести какой-нибудь более подробный анализ этого алгоритма, я буду только рад. Напишите мне разве что о результатах, мне было бы интересно.
Так а в чем провинились тесты IQ?
В самом начале статьи я написал два числовых ряда и попросил их продолжить. Это довольно частый вопрос во всяких IQ тестах. В принципе, вопрос как вопрос, но если копнуть чуть глубже, окажется, что он довольно бредовый, потому что при некотором желании можно доказать, что «правильного» ответа на него не имеется.Рассмотрим для начала ряд «2, 4, 6, 8, ?»
Представим себе этот числовой ряд как множество пар значений :

Где в качестве мы берем само число, а в качестве – порядковый номер этого числа. Какое значение должно быть на месте ?
Мысль, к которой я стараюсь плавно подвести – это то, что мы можем подставить абсолютно любое значение. Ведь что по факту проверяют такие задачи? Способность человека найти некое правило, которое связывает все имеющиеся числа, и по этому правилу вывести следующее число в последовательности. Говоря научным языком, здесь стоит задача экстраполяции (задача интерполяции состоит в том, чтобы найти кривую, проходящую через все точки внутри некоторого интервала, а задача экстраполяции – продолжить эту кривую за пределы интервала, «предсказав» таким образом поведение кривой в дальнейшем). Так вот, экстраполяция не имеет однозначного решения. Вообще. Никогда. Если бы было иначе, люди давным-давно бы предсказали прогноз погоды на всю историю человечества вперед, а скачки курса рубля никогда не были бы неожиданностью.
Разумеется, предполагается, что верный ответ в этой задаче все-таки есть и он равен 10, и тогда «закон», связывающий все эти числа, – это
Недостатки кусочно-линейной и полиномиальной интерполяции привели к разработке теории сплайн-функции (от английского слова spline - линейка, рейка). Это связано с тем, что в инженерной практике часто приходится проводить гладкие кривые, используя упругую металлическую линейку, закрепленную в узловых точках.
Рассмотрим наиболее распространенный вариант сплайн-интерполяции - интерполяцию кубическими сплайнами .
Установлено, что упругая недеформируемая линейка проходит между соседними узлами по линии, удовлетворяющей уравнению
Очевидно, если в качестве функции выбрать полином, то его степень должна быть не выше третьей, так как для полинома третьей степени четвертая производная тождественно равна нулю. Этот полином называют кубическим сплайном , который на интервале записывается в виде
где a i ,b i ,c i ,d i - коэффициенты сплайна, определяемые из дополнительных условий; i = 1,2,3,....n - номер сплайна.
Всего сплайнов на один меньше, чем точек интерполяции. Интерполяцию сплайнами можно назвать кусочно-полиномиальной.
Коэффициенты сплайнов определяются из следующих условий сшивания соседних сплайнов в узловых точках.
1. Равенство значений сплайнов и функции f(x) в узловых точках - условия Лагранжа:
![]() , . (6.10)
, . (6.10)
2. Непрерывность первой и второй производных от сплайнов в узлах:
Кроме перечисленных условий, следует добавить условия на концах, т. е. в точках x 0 и x n . В общем случае эти условия зависят от конкретной задачи. Мы воспользуемся условиями свободных концов сплайнов, т.е. вне интервала функция описывается полиномом первой степени - прямой линией:
![]() ,
, ![]() . (6.12)
. (6.12)
Условия (6.10)-(6.12) позволяют найти коэффициенты a i ,b i ,c i ,d i всех n сплайнов. Их значения выражаются следующими формулами:
 , (6.13)
, (6.13)
где в первых трех уравнениях i = 1,2,...n , а в третьем i = 2,3,..n ;
h i =x i -x i -1 - i -й шаг аргумента.
Учитывая индексацию для с i , добавим значения этого коэффициента на концах сплайна
Сначала решается система из n - 1 линейных уравнений для с i . Затем определяются b i и d i по известным коэффициентам с i , а i известно - это значения функции f(x) в узловых точках. В каждое уравнение для определения с i входит только три неизвестных с последовательными значениями индексов c i - 1 ,c i ,c i +1 . Такая матрица, имеющая отличные от нуля только элементы главной и двух соседних диагоналей, называется трехдиагональной.
Программная реализация рассмотренного алгоритма приведена ниже (ПРОГРАММА 6.2). Приведен фрагмент, в котором рассчитываются коэффициенты сплайнов по узловым значениям интерполируемой функции.
Для формирования трехдиагональной матрицы Kc использован массив шагов аргумента h i . В процедуре Gauss рассчитывается вспомогательный массив cv, имеющий на 2 элемента меньше, чем массив с., так как с 0 и c n +1 известны и равны нулю. При большом числе уравнений для решения систем с трехдиагональной матрицей применяют метод прогонки , являющийся вариантом метода последовательных исключений. Результаты расчетов с использованием интерполяции сплайнами приведены на рис.6.4. В качестве интерполируемой функции был взят ток катушки электромагнита.

Как видно на рис.6.4, интерполяция кубическими сплайнами дает очень хорошее приближение в случае, если функция гладкая. В окружности на рисунке обозначен участок, где погрешность сплайна велика. Это связано с тем, что на этом участке происходит излом кривой тока, связанный с изменением сопротивления диода R D
c прямого R пр
на обратное R обр
. При этом первая производная тока делает скачок, а сплайны по определению имеют равные первые производные справа и слева от узловой точки.
Как отмечалось ранее, интерполяция есть частный случай аппроксимации, критерием которой являются условия Лагранжа. Рассмотрим другой критерий аппроксимации - минимизацию среднеквадратичного отклонения приближающей функции от аппроксимируемой f(x) .

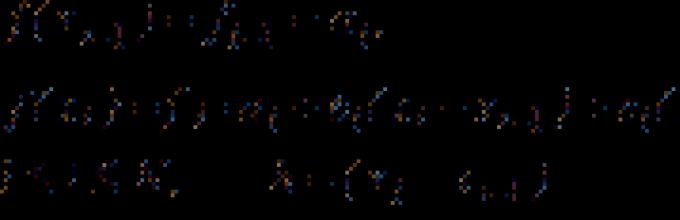

 .
.



 .
.
 .
.






