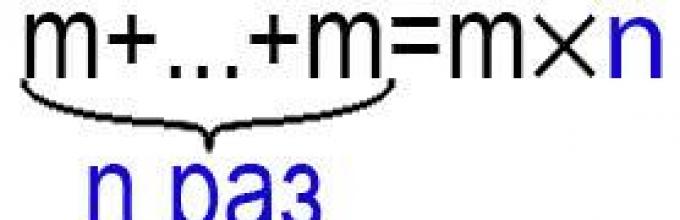Разберем понятие умножение на примере:
Туристы находились в пути три дня. Каждый день они проходили одинаковый путь по 4200 м. Какое расстояние они прошли за три дня? Решите задачу двумя способами.
Решение:
Рассмотрим задачу подробно.
В первый день туристы прошли 4200м. Во-второй день тот же самый путь прошли туристы 4200м и в третий день – 4200м. Запишем математическим языком:
4200+4200+4200=12600м.
Мы видим закономерность число 4200 повторяется три раза, следовательно, можно сумму заменить умножением:
4200⋅3=12600м.
Ответ: туристы за три дня прошли 12600 метров.
Рассмотрим пример:
Чтобы нам не писать длинную запись можно записать ее в виде умножения. Число 2 повторяется 11 раз поэтому пример с умножением будет выглядеть так:
2⋅11=22
Подведем итог. Что такое умножение?
Умножение – это действие заменяющее повторение n раз слагаемого m.

Запись m⋅n и результат этого выражения называют произведением чисел , а числа m и n называют множителями .
Рассмотрим сказанное на примере:
7⋅12=84
Выражение 7⋅12 и результат 84 называются произведением чисел
.
Числа 7 и 12 называются множителями
.
В математике есть несколько законов умножения. Рассмотрим их:
Переместительный закон умножения.
Рассмотрим задачу:
Мы отдали по два яблока 5 своим друзьям. Математически запись будет выглядеть так: 2⋅5.
Или мы отдали по 5 яблок двум своим друзьям. Математически запись будет выглядеть так: 5⋅2.
В первом и втором случаем мы раздадим одинаковое количество яблок равное 10 штукам.
Если мы умножим 2⋅5=10 и 5⋅2=10, то результат не поменяется.
Свойство переместительного закона умножения:
От перемены мест множителей произведение не меняется.
m
⋅
n
=n⋅
m
Сочетательный закон умножения.
Рассмотрим на примере:
(2⋅3)⋅4=6⋅4=24 или 2⋅(3⋅4)=2⋅12=24 получим,
(2⋅3)⋅4=2⋅(3⋅4)
(a
⋅
b
) ⋅
c
=
a
⋅(b
⋅
c
)
Свойство сочетательного закона умножения:
Чтобы число умножить на произведение двух чисел, можно его сначала умножить на первый множитель, а затем полученное произведение умножить на второй.
Меняя несколько множителей местами и заключая их в скобки, результат или произведение не изменится.
Эти законы верны для любых натуральных чисел.
Умножение любого натурального числа на единицу.
Рассмотрим пример:
7⋅1=7 или 1⋅7=7
a
⋅1=a или 1⋅
a
=
a
При умножении любого натурального числа на единицу произведением будет всегда тоже число.
Умножение любого натурального числа на нуль.
6⋅0=0 или 0⋅6=0
a
⋅0=0 или 0⋅
a
=0
При умножении любого натурального числа на нуль произведение будет равно нулю.
Вопросы к теме “Умножение”:
Что такое произведение чисел?
Ответ: произведением чисел или умножение чисел называется выражение m⋅n, где m – слагаемое, а n – число повторений этого слагаемого.
Для чего нужно умножение?
Ответ: чтобы не писать длинное сложение чисел, а писать сокращенно. Например, 3+3+3+3+3+3=3⋅6=18
Что является результатом умножения?
Ответ: значение произведения.
Что означает запись умножения 3⋅5?
Ответ: 3⋅5=5+5+5=3+3+3+3+3=15
Если умножить миллион на нуль, чему будет равно произведение?
Ответ: 0
Пример №1:
Замените сумму произведением: а) 12+12+12+12+12 б)3+3+3+3+3+3+3+3+3
Ответ: а)12⋅5=60 б) 3⋅9=27
Пример №2:
Запишите в виде произведения: а) а+а+а+а б) с+с+с+с+с+с+с
Решение:
а)а+а+а+а=4⋅а
б) с+с+с+с+с+с+с=7⋅с
Задача №1:
Мама купила 3 коробки конфет. В каждой коробке по 8 конфет. Сколько конфет купила мама?
Решение:
В одной коробке 8 конфет, а у нас таких коробок 3 штуки.
8+8+8=8⋅3=24 конфеты
Ответ: 24 конфеты.
Задача №2:
Учительница рисования сказала приготовить своим восемью ученикам по семь карандашей на урок. Сколько всего карандашей вместе было у детей?
Решение:
Можно посчитать суммой задачу. У первого ученика было 7 карандашей, у второго ученика было 7 карандашей и т.д.
7+7+7+7+7+7+7+7=56
Запись получилась неудобная и длинная, заменим сумму на произведение.
7⋅8=56
Ответ 56 карандашей.
В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения. Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Наследие индусов - способ решётки.
Индусы, с давних времён знавшие десятичную систему счисления, пред почитали устный счёт письменному. Они изобрели несколько способов быстрого умножения . Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, - умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в средние века он широко распространился на Востоке, а в эпоху возрождения - в Европе. Способ решётки именовали также индийским, мусульманским или "Умножением в Клеточку". А в Италии его называли "Джелозия", или "решётчатое умножение" (Gelosia в переводе с итальянского - "жалюзи", "решётчатые ставни". Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями - жалюзи, которые закрывали от солнца окна венецианских домов.

Суть этого нехитрого способа умножения поясним на примере: мы вычислим произведение 296 x 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, - по количеству цифр в множителях. Клетки пополам по диагонали разделим. Над таблицей запишем число 296, а с правой стороны вертикально - число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения сложением цифр в косых полосах получим. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 1 7 и т. д. запишем результаты под таблицей, а также слева от неё. В том случае, если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы. Ответ: 21 608. Итак, 296 x 73 = 21 608.

Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.

Почему способ решётки приводит к правильному ответу? В чём заключается его "Механизм"? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 90 6 и 70 3.

Как видим, в первой косой полосе стоят единицы, во второй - десятки, в третьей - сотни и т. д. при сложении они дают в ответе соответственно число единиц, десятков, сотен и т. д. дальнейшее очевидно:
10 10 1500. 100. 8 _ 21608.
Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 90 6) x (70 3) = 14 000 6300 420 600 270 18 = 10 000 (4000 6000) (300 400 600 200) (70 20 10) 8 = 21 608.
Палочки непера.
Умножение способом решётки лежит в основе простого и оригинального счётного прибора - палочек непера.
Его изобретатель Джон непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней - число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек непера легко умножать многозначные числа, сводя эту операцию к сложению.
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие - с цифрами 2, 9 и 6 наверху (они должны образовать число 296. Теперь заглянем в третью строку (номера строк указаны на крайней линейке. Цифры в ней уже знакомый нам набор образуют.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, ра? 6
В школе изучают таблицу умножения, а затем учат детей умножать числа в столбик. Разумеется, это не единственный способ умножения. На самом деле, существовало несколько десятков способов умножения и деления многозначных чисел. Приведу здесь, возможно, даже более простой “метод решетки” (см. книгу И.Я. Депман, Н.Я. Виленкин “За страницами учебника ”). Рассмотрим этот метод на примере.
Пусть нужно умножить 347 на 29 . Начертим таблицу, как на рисунке а), запишем над ней число 347 слева направо, а справа от нее – число 29 сверху вниз. В каждую клеточку запишем произведение цифр, стоящих над этой клеточкой и справа от нее. При этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. А теперь будем складывать цифры в каждой косой полосе, показанные на рисунке, выполняя эту операцию справа налево. Если сумма окажется меньше 10 , то ее пишут под нижней цифрой полосы. Если же она окажется больше 10 , то пишут только цифру единиц суммы, а цифру десятков прибавляют к следующей сумме. В результате получаем нужное произведение, которое равно 10063 .

Этот способ умножения раньше был распространен на Востоке и в Италии. Чтобы понять его смысл, посмотрим на рисунок б). Видим, что в первой полосе стоят единицы, во второй – десятки, в третьей – сотни и т.д. Иными словами, произведение 347\cdot29 вычисляется следующим образом:

Есть еще некоторые правила, помогающие быстрому счету. Так, чтобы возвести в квадрат двузначное число , оканчивающееся на 5 , нужно к первой цифре прибавить 1 и умножить полученное число на эту цифру, а потом к полученному результату приписать 25 . Например, возведем в квадрат 35 . Первая цифра этого числа 3 , прибавим 1: 3+1=4 . Умножим 3 на 4 , получим 12 , дальше просто припишем 25 . Итак, ответ: 1225 .
Такое правило следует сразу же из того, что
Разумеется, так можно возводить в квадрат и трехзначные числа, оканчивающиеся на 5, и числа, которые имеют еще больше знаков. Однако в этих случаях придется вычислять произведение a\cdot(a+1) , где в числе a уже несколько десятичных знаков, а это тоже приходится делать, скажем, в столбик, то есть это уже сложнее!
А теперь на видео представлен метод умножения, бурно просматриваемый и обсуждаемый в Интернете, который называют китайским. Забавно и интересно. Кстати сказать, выложены уже некоторые обобщения этого способа, потому что проводить 9 прямых при умножении на 9 как-то долго и неинтересно, а потом еще точки пересечения считать… В общем, таблицу умножения все-таки знать нужно! Думаю, вы сами сможете объяснить, почему метод работает. Внимание, вопрос: так почему же?
Что такое умножение?
Умножение - это арифметическое действие , в котором первое число повторяется в качестве слагаемого столько раз, сколько показывает второе число.
Число, которое повторяется как слагаемое, называется множимым (оно умножается), число, которое показывает сколько раз повторить слагаемое, называется множителем . Число, полученное в результате умножения, называется произведением .
Например, умножить натуральное число 2 на натуральное число 5 - значит найти сумму пяти слагаемых, каждое из которых равно 2:
2 + 2 + 2 + 2 + 2 = 10
В этом примере мы находим сумму обыкновенным сложением. Но когда число равных слагаемых велико, нахождение суммы посредством сложения всех слагаемых становится слишком утомительным делом.
Умножение обозначается знаком × (косой крест) или знаком · (точка) и читается: умножить на. Знак умножения ставится между множимым и множителем. Множимое записывается слева от знака умножения, а множитель - справа:
Эта запись читается так: произведение 2 и 5 равняется 10 или 2 умножить на 5 равно 10 .
Таким образом, мы видим, что умножение представляет собой просто краткую форму записи сложения одинаковых слагаемых.
Проверка умножения
Для проверки умножения можно произведение разделить на множитель. Если в результате деления получится число, равное множимому, то умножение сделано верно:
Теперь выполним проверку умножения:
Умножение также можно проверить разделив произведение на множимое. Если в результате деления получится число, равное множителю, то умножение сделано верно:
Выполним проверку:
Умножение единицы и на единицу
a верны равенства:
1 · a
= a
a
· 1 = a
- Если множимое является числом 1, то произведение равно множителю. Например, 1 · 3 = 3, потому что сумма 1 + 1 + 1 равна трём.
- Если множитель единица, то произведение будет равно множимому. Например, 5 · 1 = 5. Если число 5 взять 1 раз, получим 5.
Число 0 в умножении
Для любого натурального числа a верны равенства:
a
· 0 = 0
0 · a
= 0
Эти равенства означают следующее:
- Если множитель является нулём, то произведение равно нулю. Например, 5 · 0 = 0 (если 5 не брать ни одного раза, то естественно, ничего не получим).
- Если множимое является числом нуль, то и произведение равно нулю. Например, 0 · 3 = 0, потому что сумма 0 + 0 + 0 равна нулю.
Сочетательное свойство умножения указывает нам на равенство двух произведений a·(b·c) и (a·b)·c , где a , b и c – какие угодно натуральные числа. Таким образом, результат умножения трех чисел a , b и c не зависит от способа расстановки скобок. Из-за этого в произведениях a·(b·c) и (a·b)·c скобки часто не ставят, а произведения записывают в виде a·b·c . Выражение a·b·c называют произведением трех чисел a , b и c , числа a , b и c все также называют множителями.
Аналогично, сочетательное свойство умножения позволяет утверждать, что произведения (a·b)·(c·d) , (a·(b·c))·d , ((a·b)·c)·d , a·(b·(c·d)) и a·((b·c)·d) равны. То есть, результат умножения четырех чисел тоже не зависит от распределения скобок. Произведение четырех чисел a , b , c и d записывают как a·b·c·d .
Вообще, результат умножения двух, трех, четырех и так далее чисел не зависит от способа расстановки скобок и в записи таких произведений скобки обычно опускаются.
Теперь разберемся, как вычисляется произведение нескольких чисел, в записи которого не расставлены скобки. В этом случае умножение трех и более чисел сводится к последовательной замене двух соседних множителей их произведением , пока не получим требуемый результат. Иными словами, в записи произведения мы расставляем скобки самостоятельно любым допустимым способом, после чего последовательно выполняем умножение двух чисел.
Рассмотрим пример вычисления произведения пяти натуральных чисел 2 , 1 , 3 , 1 и 8 . Запишем произведение: 2·1·3·1·8 . Покажем два способа решения (всего способов решения больше, чем два).
Первый способ. Будем последовательно заменять два множителя слева их произведением. Так как результатом умножения чисел 2 и 1 является число 2 , то 2·1·3·1·8=2·3·1·8 . Так как 2·3=6 , то 2·3·1·8=6·1·8 . Дальше, так как 6·1=6 , то 6·1·8=6·8 . Наконец, 6·8=48 . Итак, произведение пяти чисел 2 , 1 , 3 , 1 и 8 равно 48 . Это решение соответствует следующему способу расстановки скобок: (((2·1)·3)·1)·8 .
Второй способ. Расставим скобки в произведении так: ((2·1)·3)·(1·8) . Так как 2·1=2 и 1·8=8 , то ((2·1)·3)·(1·8)=(2·3)·8 . Дважды три – это шесть, тогда (2·3)·8=6·8 . Наконец, 6·8=48 . Итак, 2·1·3·1·8=48 .
Заметим, что на результат умножения трех и более чисел не влияет также порядок следования множителей. Другими словами, множители в произведении можно записывать в любом порядке, а также менять их местами. Это утверждение следует из свойств умножения натуральных чисел.
Рассмотрим пример.
Умножим четыре числа 3 , 9 , 2 и 1 . Запишем их произведение: 3·9·2·1 . Если мы заменим множители 3 и 9 их произведением или множители 9 и 2 их произведением, то на следующем этапе нам придется проводить умножение на двузначные числа 27 или 18 (чего мы пока делать не умеем). Можно обойтись без этого, поменяв местами слагаемые и определенным образом расставив скобки. Имеем, 3·9·2·1=3·2·9·1=(3·2)·(9·1)=6·9=54 .
Таким образом, меняя местами множители, мы можем вычислять произведения наиболее удобным способом.
Для полноты картины рассмотрим задачу, решение которой сводится к умножению нескольких чисел.
В каждой коробке находится 3 предмета. В каждый ящик уложено 2 коробки. Сколько предметов содержится в 4 ящиках?
Так как в одном ящике находятся 2 коробки, в каждой из которых 3 предмета, то в одном ящике находится 3·2=6 предметов. Тогда в четырех ящиках находится 6·4=24 предмета.
Можно рассуждать иначе. Так как в одном ящике находятся 2 коробки, тогда в четырех ящиках находятся 2·4=8 коробок. Так как в каждой коробке лежат 3 предмета, то в 8 коробках лежат 3·8=24 предмета.
Озвученные решения кратко можно записать как (3·2)·4=6·4=24 или 3·(2·4)=3·8=24 .
Таким образом, искомое количество предметов равно произведению чисел 3 , 2 и 4 , то есть, 3·2·4=24 .
Подытожим информацию этого пункта.
Умножение трех и более натуральных чисел представляет собой последовательное умножение двух чисел. Кроме того, в силу переместительного и сочетательного свойств умножения, множители можно менять местами и заменять любые два из умножаемых чисел их произведением.
Умножение суммы на натуральное число и натурального числа на сумму.
Сложение и умножение чисел связаны распределительным свойством умножения. Это свойство позволяет изучать сложение и умножение совместно, что открывает гораздо больше возможностей, чем раздельное изучение этих действий.
Распределительное свойство умножения относительно сложения мы сформулировали для двух слагаемых: (a+b)·c=a·c+b·c , a , b , c – произвольные натуральные числа. Отталкиваясь от этого равенства, можно доказать справедливость равенств (a+b+c)·d=a·d+b·d+c·d , (a+b+c+d)·h=a·h+b·h+c·h+d·h и т.д., a , b , c , d , h – некоторые натуральные числа.
Таким образом, произведение суммы нескольких чисел и данного числа равно сумме произведений каждого из слагаемых и данного числа. Этим правилом можно пользоваться при умножении суммы на данное число.
Для примера, умножим сумму пяти чисел 7 , 2 , 3 , 8 , 8 на число 3 . Воспользуемся полученным правилом: (7+2+3+8+8)·3=7·3+2·3+3·3+8·3+8·3 . Так как 7·3=21 , 2·3=6 , 3·3=9 , 8·3=24 , то 7·3+2·3+3·3+8·3+8·3=21+6+9+24+24 . Осталось вычислить сумму пяти чисел 21+6+9+24+24=84 .
Конечно, можно было сначала вычислить сумму пяти данных чисел, после чего провести умножение. Но в этом случае нам бы пришлось умножать двузначное число 7+2+3+8+8=28 на число 3 , чего мы делать пока не умеем (об умножении таких чисел мы поговорим позже в разделе).
Переместительное свойство умножения позволяет нам переформулировать правило умножения суммы чисел на данное число следующим образом: произведение данного числа и суммы нескольких чисел равно сумме произведений данного числа и каждого из слагаемых. Это есть правило умножения данного числа на сумму.
Приведем пример использования правила умножения числа на сумму: 2·(6+1+3)=2·6+2·1+2·3=12+2+6=20 .
Давайте рассмотрим задачу, решение которой сводится к умножению суммы чисел на данное число.
В каждой коробке находятся 3 красных, 7 зеленых и 2 синих предмета. Сколько всего предметов находится в четырех коробках?
В одной коробке находятся 3+7+2 предметов. Тогда в четырех коробках находятся (3+7+2)·4 предметов. Вычислим произведение суммы на число, используя полученное правило: (3+7+2)·4=3·4+7·4+2·4=12+28+8=48 .
48 предметов.
Умножение натурального числа на 10 , 100 , 1 000 и так далее.
Для начала получим правило умножения произвольного натурального числа на 10 .
Натуральные числа 20
, 30
, …, 90
по своей сути соответствуют 2
десяткам, 3
десяткам, …, 9
десяткам, то есть, 20=10+10
, 30=10+10+10
, … Так как умножению двух натуральных чисел мы придали смысл суммы одинаковых слагаемых, то имеем
2·10=20
, 3·10=30
, ..., 9·10=90
.
Рассуждая аналогично, приходим к следующим равенствам:
2·100=200
, 3·100=300
, ..., 9·100=900
;
2·1 000=2 000
, 3·1 000=3 000
, ..., 9·1 000=9 000
;
2·10 000=20 000
, 3·10 000=30 000
, ..., 9·10 000=90 000
; ...
Так как десяток десятков есть сотня, то 10·10=100
;
так как десяток сотен есть тысяча, то 100·10=1 000
;
так как десяток тысяч есть десять тысяч, то 1 000·10=10 000
.
Продолжая эти рассуждения, имеем 10 000·10=100 000
, 100 000·10=1 000 000
, …
Давайте теперь рассмотрим пример, который позволит нам сформулировать правило умножения произвольного натурального числа на десять.
Умножим натуральное число 7 032 на 10 .
Для этого число 7 032 представим в виде суммы разрядных слагаемых, после чего воспользуемся правилом умножения суммы на число, которое мы получили в предыдущем пункте этой статьи: 7 032·10=(7 000+30+2)·10= 7 000·10+30·10+2·10 .
Так как 7 000=7·1 000
и 30=3·10
, то полученная сумма 7 000·10+30·10+2·10
равна сумме (7·1 000)·10+(3·10)·10+2·10
, а сочетательное свойство умножения позволяет записать следующее равенство:
(7·1 000)·10+(3·10)·10+2·10=
7·(1 000·10)+3·(10·10)+2·10
.
В силу результатов, записанных перед этим примером, имеем 7·(1 000·10)+3·(10·10)+2·10= 7·10 000+3·100+2·10= 70 000+300+20 .
Полученная сумма 70 000+300+20 представляет собой разложение по разрядам числа 70 320 .
7 032·10=70 320 .
Выполняя аналогичные действия, мы можем умножить любое натуральное число на десять. При этом не сложно заметить, что в результате мы будем получать числа, запись которых будет отличаться от записи умножаемого числа лишь цифрой 0 , находящейся справа.
Все приведенные рассуждения позволяют нам озвучить правило умножения произвольного натурального числа на десять : если в записи данного натурального числа справа дописать цифру 0 , то полученная запись будет соответствовать числу, которое является результатом умножения данного натурального числа на 10 .
Например, 4·10=40 , 43·10=430 , 501·10=5 010 , 79 020·10=790 200 и т.п.
А теперь на основании правила умножения натурального числа на 10 , мы можем получить правила умножения произвольного натурального числа на 100 , на 1 000 и т.д.
Так как 100=10·10
, то умножение любого натурального числа на 100
сводится к умножению этого числа на 10
10
. Например,
17·100=17·10·10=170·10=1 700
;
504·100=504·10·10=5 040·10=50 400
;
100 497·100=100 497·10·10= 1 004 970·10=10 049 700
.
То есть, если справа в записи умножаемого числа приписать справа две цифры 0 , то получим результат умножения этого числа на 100 . Это и есть правило умножения натурального числа на 100 .
Так как 1 000=100·10 , то умножение любого натурального числа на тысячу сводится к умножению этого числа на 100 и последующему умножению полученного результата на 10 . Из этих рассуждений следует правило умножения произвольного натурального числа на 1 000 : если в записи числа справа дописать три цифры 0 , то получим результат умножения этого числа на тысячу.
Аналогично, при умножении натурального числа на 10 000 , 100 000 и так далее нужно дописать справа соответственно четыре цифры 0 , пять цифр 0 и так далее.
Например,
58·1 000=58 000
;
6 032·1 000 000=6 032 000 000
;
777·10 000=7 770 000
.
Умножение многозначного и однозначного натуральных чисел.
Теперь мы обладаем всеми навыками, достаточными для выполнения умножения многозначного и однозначного натуральных чисел.
Что же для этого нужно делать?
Давайте сразу разбираться на примере.
Умножим трехзначное число 763 на однозначное число 5 , то есть, вычислим произведение 763·5 .
Сначала нужно представить многозначное число в виде суммы разрядных слагаемых. В нашем примере 763=700+60+3 , тогда имеем 763·5=(700+60+3)·5 .
Теперь применяем: (700+60+3)·5=700·5+60·5+3·5 .
Так как 700=7·100 и 60=6·10 (об этом мы говорили в предыдущем пункте), то сумму 700·5+60·5+3·5 можно записать как (7·100)·5+(6·10)·5+3·5 .
В силу переместительного и сочетательного свойств умножения справедливо следующее равенство: (7·100)·5+(6·10)·5+3·5= (5·7)·100+(5·6)·10+3·5 .
Так как 5·7=35 , 5·6=30 и 3·5=15 , то (5·7)·100+(5·6)·10+3·5= 35·100+30·10+15 .
Осталось выполнить умножение на 100
и на 10
, после чего выполнить сложение трех слагаемых:
35·100+30·10+15=
3 500+300+15=3 815
Произведение 763 и 5 равно 3 815 .
Понятно, что умножение однозначного числа на многозначное число проводится подобным образом.
Для закрепления материала приведем решение еще одного примера, но в этот раз обойдемся без пояснений.
3 и 104 558 .
3·104 558=
3·(100 000+4 000+500+50+8)=
=3·100 000+3·4 000+
3·500+3·50+3·8=
=3·100 000+3·(4·1 000)+
3·(5·100)+3·(5·10)+3·8=
=3·100 000+(3·4)·1 000+
(3·5)·100+(3·5)·10+3·8=
=3·100 000+12·1 000+
15·100+15·10+3·8=
=300 000+12 000+
1 500+150+24=313 674
Результатом умножения чисел 3 и 104 558 является число 313 674 .
Умножение двух многозначных натуральных чисел.
Вот мы и подошли к кульминации – к умножению двух многозначных натуральных чисел. Первым делом нужно один из множителей разложить по разрядам (обычно раскладывается то число, запись которого состоит из большего числа знаков), после этого воспользоваться правилом умножения числа на сумму (или суммы на число). Дальнейшие вычисления не вызовут трудностей, если Вы хорошо усвоили информацию предыдущих разделов этой статьи.
Разберем все этапы умножения двух многозначных натуральных чисел на примере.
Вычислите произведение чисел 41 и 3 806 .
Разложение натурального числа 3 806 по разрядам имеет вид 3 000+800+6 , поэтому, 41·3 806=41·(3 000+800+6) .
Применим правило умножения числа на сумму: 41·(3 000+800+6)= 41·3 000+41·800+41·6 .
Так как 3 000=3·1 000 и 800=8·100 , то справедливо равенство 41·3 000+41·800+41·6= 41·(3·1 000)+41·(8·100)+41·6 .
Сочетательное свойство умножения позволяет нам переписать последнюю сумму в следующем виде (41·3)·1 000+(41·8)·100+41·6 .
И умножение. Как раз об операции умножения и пойдет речь в этой статье.
Умножение чисел
Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.
Пример 2*5 . Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.
Пример 4*3 . Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.
Пример 5*3 . Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.
Формулы умножения
Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:
Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.
Сокращенное умножение
Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. Которые помогут сделать вычисления наиболее рациональными и быстрыми:
Формулы сокращенного умножения
Пусть a, b принадлежат R, тогда:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a+b)^2 = a^2 + 2ab + b^2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения. Формула: (a-b)^2 = a^2 - 2ab + b^2
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Формула: a^2 - b^2 = (a - b)(a + b)
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. Формула: (a + b)^3 = a^3 + 3a(^2)b + 3ab^2 + b^3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. Формула: (a-b)^3 = a^3 - 3a(^2)b + 3ab^2 - b^3
Сумма кубов a^3 + b^3 = (a + b)(a^2 - ab + b^2)
Разность кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений. Формула: a^3 - b^3 = (a - b)(a^2 + ab + b^2)
Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Умножение дробей
Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо ! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.
Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс
Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:
Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?
В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?
Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?
В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?
Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?
В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?
Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?
В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс
В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление .
Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.
Умножение столбиком:
Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.
![]()
1 шаг . Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг . Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.
Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг . Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг . Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.
Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!
5 шаг . Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг . Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс
Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.
Например, найти произведение следующих пар чисел:
- 988 * 98 =
- 99 * 114 =
- 17 * 174 =
- 164 * 19 =

Презентация на умножение
Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!
Таблица умножения
Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Примеры на умножение
Умножение на однозначное
- 9 * 5 =
- 9 * 8 =
- 8 * 4 =
- 3 * 9 =
- 7 * 4 =
- 9 * 5 =
- 8 * 8 =
- 6 * 9 =
- 6 * 7 =
- 9 * 2 =
- 8 * 5 =
- 3 * 6 =
Умножение на двузначное
- 4 * 16 =
- 11 * 6 =
- 24 * 3 =
- 9 * 19 =
- 16 * 8 =
- 27 * 5 =
- 4 * 31 =
- 17 * 5 =
- 28 * 2 =
- 12 * 9 =
Умножение двузначное на двузначное
- 24 * 16 =
- 14 * 17 =
- 19 * 31 =
- 18 * 18 =
- 10 * 15 =
- 15 * 40 =
- 31 * 27 =
- 23 * 25 =
- 17 * 13 =
Умножение трехзначных чисел
- 630 * 50 =
- 123 * 8 =
- 201 * 18 =
- 282 * 72 =
- 96 * 660 =
- 910 * 7 =
- 428 * 37 =
- 920 * 14 =

Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра "Быстрый счет"
Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра "Математические матрицы"
«Математические матрицы» великолепное упражнение для мозга детей , которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра "Числовой охват"
Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.
Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра "Угадай операцию"
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Упрощение"
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Быстрое сложение"
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Визуальная геометрия"
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра "Математические сравнения"
Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Умножить одно целое число на другое значит повторить одно число столько раз, сколько в другом содержится единиц. Повторить число значит взять его слагаемым несколько раз и определить сумму.
Определение умножения
Умножение целых чисел есть такое действие, в котором нужно взять одно число слагаемым столько раз, сколько в другом содержится единиц, и найти сумму этих слагаемых.
Умножить 7 на 3 значит взять число 7 слагаемым три раза и найти сумму. Искомая сумма есть 21.
Умножение есть сложение равных слагаемых .
Данные в умножении называются множимым и множителем , а искомое - произведением .
В предложенном примере данными будут множимое 7, множитель 3, а искомым произведением 21.
Множимое . Множимое есть то число, которое умножается или повторяется слагаемым. Множимое выражает величину равных слагаемых.
Множитель . Множитель показывает, сколько раз множимое повторяется слагаемым. Множитель показывает число равных слагаемых.
Произведение . Произведение есть число, которое получается от умножения. Оно есть сумма равных слагаемых.
Множимое и множитель вместе называются производителями .
При умножении целых чисел одно число увеличивается во столько раз, сколько в другом содержится единиц.
Знак умножения . Действие умножения обозначают знаком × (косвенным крестом) или. (точкой). Знак умножения ставится между множимым и множителем.
Повторить число 7 три раза слагаемым и найти сумму значит 7 умножить на 3. Вместо того, чтобы писать
пишут при помощи знака умножения короче:
7 × 3 или 7 · 3
Умножение есть сокращенное сложение равных слагаемых.
Знак (× ) был введен Отредом (1631 г.), а знак. Христианом Вольфом (1752 г.).
Связь между данными и искомым числом выражается в умножении
письменно:
7 × 3 = 21 или 7 · 3 = 21
словесно:
семь, умноженное на три, составляет 21.
Чтобы составить произведение 21, нужно 7 повторить три раза
Чтобы составить множитель 3, нужно единицу повторить три раза
Отсюда имеем другое определение умножения : Умножение есть такое действие, в котором произведение точно так же составляется из множимого, как множитель составлен из единицы.
Основное свойство произведения
Произведение не изменяется от перемены порядка производителей.
Доказательство . Умножить 7 на 3 значит 7 повторить три раза. Заменив 7 суммою 7 единиц и вложив их в вертикальном порядке, имеем:
Таким образом, при умножении двух чисел мы можем считать множителем любой из двух производителей. На этом основании производители называются сомножителями или просто множителями .
Самый общий прием умножения состоит в сложении равных слагаемых; но, если производители велики, этот прием приводит к длинным вычислениям, поэтому самое вычисление располагают иначе.
Умножение однозначных чисел. Таблица Пифагора
Чтобы умножить два однозначных числа, нужно повторить одно число слагаемым столько раз, сколько в другом содержится единиц, и найти их сумму. Так как умножение целых чисел приводится к умножению однозначных чисел, то составляют таблицу произведений всех однозначных чисел попарно. Такая таблица всех произведений однозначных чисел попарно называется таблицей умножения .
Изобретение ее приписывают греческому философу Пифагору, по имени которого ее называют таблицей Пифагора . (Пифагор родился около 569 года до н. э.).
Чтобы составить эту таблицу, нужно написать первые 9 чисел в горизонтальный ряд:
1, 2, 3, 4, 5, 6, 7, 8, 9.
Затем под этой строкой надо подписать ряд чисел, выражающих произведение этих чисел на 2. Этот ряд чисел получится, когда в первой строке сложим каждое число само с собою. От второй строки чисел последовательно переходим к 3, 4 и т. д. Каждая последующая строка получается из предыдущей через прибавление к ней чисел первой строки.
Продолжая так поступать до 9 строки, мы получим таблицу Пифагора в следующем виде

Чтобы по этой таблице найти произведение двух однозначных чисел, нужно отыскать одного производителя в первой горизонтальной строке, а другого в первом вертикальном столбце; тогда искомое произведение будет на пересечении соответствующих столбца и строки. Таким образом, произведение 6 × 7 = 42 находится на пересечении 6-й строки и 7-го столбца. Произведение нуля на число и числа на нуль всегда дает нуль.
Так как произведение числа на 1 дает само число и перемена порядка множителей не изменяет произведения, то все различные произведения двух однозначных чисел, на которые следует обратить внимание, заключаются в следующей таблице:

Произведения однозначных чисел, не содержащиеся в этой таблице, получаются по данным, если только изменить в них порядок множителе; таким образом, 9 × 4 = 4 × 9 = 36.
Умножение многозначного числа на однозначное
Умножение числа 8094 на 3 обозначают тем, что подписывают множитель под множимым, ставят слева знак умножения и проводят черту с тем, чтобы отделить произведение.
Умножить многозначное число 8094 на 3 значит найти сумму трех равных слагаемых
следовательно, для умножения нужно все порядки многозначного числа повторить три раза, то есть умножить на 3 единицы, десятки, сотни, и т. п. Сложение начинают с единицы, следовательно, и умножение нужно начинать с единицы, а затем переходят от правой руки к левой к единицам высшего порядка.
При этом ход вычислений выражают словесно:
Начинаем умножение с единиц : 3 × 4 составляют 12, подписываем под единицами 2, а единицу (1 десяток) прикладываем к произведению следующего порядка на множитель (или запоминаем ее в уме).
Умножаем десятки : 3 × 9 составляет 27, да 1 в уме составят 28; подписываем под десятками 8 и 2 в уме.
Умножаем сотни : Нуль, умноженный на 3, дает нуль, да 2 в уме составит 2, подписываем под сотнями 2.
Умножаем тысячи : 3 × 8 = 24, подписываем вполне 24, ибо не имеем следующих порядков.
Это действие выразится письменно:

Из предыдущего примера выводим следующее правило. Чтобы умножить многозначное число на однозначное, нужно :
Подписать множитель под единицами множимого, поставить слева знак умножения и провести черту.
Умножение начинать с простых единиц, затем, переходя от правой руки к левой, последовательно умножают десятки, сотни, тысячи и т. д.
Если при умножении произведение выражается однозначным числом, то его подписывают под умножаемой цифрой множимого.
Если же произведение выражается двухзначным числом, то цифру единиц подписывают под тем же столбцом, а цифру десятков прибавляют к произведению следующего порядка на множитель.
Умножение продолжается до тех пор, пока не получат полного произведения.
Умножение чисел на 10, 100, 1000 …
Умножить числа на 10 значит простые единицы превратить в десятки, десятки в сотни и т. д., то есть повысить порядок всех цифр на единицу. Этого достигают, прибавляя справа один нуль. Умножить на 100 значит повысить все порядки множимого двумя единицами, то есть превратить единицы в сотни, десятки в тысячи и т. д.
Этого достигают, приписывая к числу два нуля.
Отсюда заключаем:
Для умножения целого числа на 10, 100, 1000 и вообще на 1 с нулями нужно приписать справа столько нулей, сколько их находится во множителе.
Умножение числа 6035 на 1000 выразится письменно:

Когда множитель есть число, оканчивающееся нулями, подписывают под множимым только значащие цифры, а нули множителя приписывают справа.
Чтобы умножить 2039 на 300 нужно взять число 2029 слагаемым 300 раз. Взять 300 слагаемых все-равно, что взять три раза по 100 слагаемых или 100 раз по три слагаемых. Для этого умножаем число на 3, а потом на 100, или умножаем сначала на 3, а потом приписываем справа два нуля.
Ход вычисления выразится письменно:

Правило . Чтобы умножить одно число на другое, изображаемое цифрой с нулями, нужно сначала помножить множимое на число, выражаемое значащей цифрой, и затем приписать столько нулей, сколько их находится в множителе.
Умножение многозначного числа на многозначное
Чтобы умножить многозначное число 3029 на многозначное 429, или найти произведение 3029 * 429, нужно повторить 3029 слагаемым 429 раз и найти сумму. Повторить 3029 слагаемым 429 раз значит повторить его слагаемым сначала 9, потом 20 и, наконец, 400 раз. Следовательно, чтобы умножить 3029 на 429, нужно 3029 умножить сначала на 9, потом на 20 и, наконец, на 400 и найти сумму этих трех произведений.
Три произведения

называются частными произведениями .
Полное произведение 3029 × 429 равно сумме трех частных:
3029 × 429 = 3029 × 9 + 3029 × 20 + 3029 × 400.
Найдем величины этих трех частных произведений.
Умножая 3029 на 9, находим:
3029 × 9 27261 первое частное произведение
Умножая 3029 на 20, находим:
3029 × 20 60580 второе частное произведение
Умножая 3026 на 400, находим:
3029 × 400 1211600 третье частно произведение
Сложив эти частные произведения, получим произведение 3029 × 429:

Не трудно заметить, что все эти частные произведения есть произведения числа 3029 на однозначные числа 9, 2, 4, причем ко второму произведению, происходящему от умножения на десятки, приписывается один нуль, к третьему два нуля.
Нули, приписываемые к частным произведениям, опускают при умножении и ход вычисления выражают письменно:

В таком случае, при умножении на 2 (цифру десятков множителя) подписывают 8 под десятками, или отступают влево на одну цифру; при умножении на цифру сотен 4, подписывают 6 в третьем столбце, или отступают влево на 2 цифры. Вообще каждое частное произведение начинают подписывать от правой руки к левой под тем порядком, к которому принадлежит цифра множителя.
Отыскивая произведение 3247 на 209, имеем:

Здесь второе частное произведение начинаем подписывать под третьим столбцом, ибо оно выражает произведение 3247 на 2, третью цифру множителя.
Мы здесь опустили только два нуля, которые должны были явиться во втором частном произведении, как как оно выражает произведение числа на 2 сотни или на 200.
Из всего сказанного выводим правило. Чтобы умножить многозначное число на многозначное,
нужно множителя подписать под множимым так, чтобы цифры одинаковых порядков находились в одном вертикальном столбце, поставить слева знак умножения и провести черту.
Умножение начинают с простых единиц, затем переходят от правой руки к левой, умножают последовательное множимое на цифру десятков, сотен и т. д. и составляют столько частных произведений, сколько значащих цифр во множителе.
Единицы каждого частного произведения подписывают под тем столбцом, к которому принадлежит цифра множителя.
Все частные произведения, найденные таким образом, складывают вместе и получают в сумме произведение.
Чтобы умножить многозначное число на множитель, оканчивающейся нулями, нужно отбросить нули во множителе, умножить на оставшееся число и потом приписать к произведению столько нулей, сколько их находится во множителе.
Пример . Найти произведение 342 на 2700.

Если множимое и множитель оба оканчиваются нулями, при умножении отбрасывают их и затем к произведению приписывают столько нулей, сколько их содержится в обоих производителях.
Пример . Вычисляя произведение 2700 на 35000, умножаем 27 на 35
Приписывая к 945 пять нулей, получаем искомое произведение:
2700 × 35000 = 94500000.
Число цифр произведения . Число цифр произведения 3728 × 496 можно определить следующим образом. Это произведение более 3728 × 100 и меньше 3728 × 1000. Число цифр первого произведения 6 равно числу цифр в множимом 3728 и во множителе 496 без единицы. Число цифр второго произведения 7 равно числу цифр во множимом и во множителе. Данное произведение 3728 × 496 не может иметь цифр менее 6 (числа цифр произведения 3728 × 100, и более 7 (числа цифр произведения 3728 × 1000).
Откуда заключаем: число цифр всякого произведения или равно числу цифр во множимом и во множителе, или равно этому числу без единицы .
В нашем произведении может содержаться или 7 или 6 цифр.
Степени
Между различными произведениями заслуживают особого внимания такие, в которых производители равны. Так, например:
2 × 2 = 4, 3 × 3 = 9.
Квадраты . Произведение двух равных множителей называется квадратом числа.
В наших примерах 4 есть квадрат 2, 9 есть квадрат 3.
Кубы . Произведение трех равных множителей называется кубом числа.
Так, в примерах 2 × 2 × 2 = 8, 3 × 3 × 3 = 27, число 8 есть куб 2, 27 есть куб 3.
Вообще произведение нескольких равных множителей называется степенью числа . Степени получают свои названия от числа равных множителей.
Произведения двух равных множителей или квадраты называются вторыми степенями .
Произведения трех равных множителей или кубы называются третьими степенями , и т. д.