Задачей множественной линейной регрессии является построение линейной модели связи между набором непрерывных предикторов и непрерывной зависимой переменной. Часто используется следующее регрессионное уравнение:

Здесь а i - регрессионные коэффициенты, b 0 - свободный член(если он используется), е - член, содержащий ошибку - по поводу него делаются различные предположения, которые, однако, чаще сводятся к нормальности распределения с нулевым вектором мат. ожидания и корреляционной матрицей .

Такой линейной моделью хорошо описываются многие задачи в различных предметных областях, например, экономике, промышленности, медицине. Это происходит потому, что некоторые задачи линейны по своей природе.

Приведем простой пример. Пусть требуется предсказать стоимость прокладки дороги по известным ее параметрам. При этом у нас есть данные о уже проложенных дорогах с указанием протяженности, глубины обсыпки, количества рабочего материала, числе рабочих и так далее.

Ясно, что стоимость дороги в итоге станет равной сумме стоимостей всех этих факторов в отдельности. Потребуется некоторое количество, например, щебня, с известной стоимостью за тонну, некоторое количество асфальта также с известной стоимостью.

Возможно, для прокладки придется вырубать лес, что также приведет к дополнительным затратам. Все это вместе даст стоимость создания дороги.

При этом в модель войдет свободный член, который, например, будет отвечать за организационные расходы (которые примерно одинаковы для всех строительно-монтажных работ данного уровня) или налоговые отчисления.

Ошибка будет включать в себя факторы, которые мы не учли при построении модели (например, погоду при строительстве - ее вообще учесть невозможно).

Пример: множественный регрессионный анализ

Для этого примера будут анализироваться несколько возможных корреляций уровня бедности и степень, которая предсказывает процент семей, находящихся за чертой бедности. Следовательно мы будем считать переменную характерезующую процент семей, находящихся за чертой бедности, - зависимой переменной, а остальные переменные непрерывными предикторами.

Коэффициенты регрессии

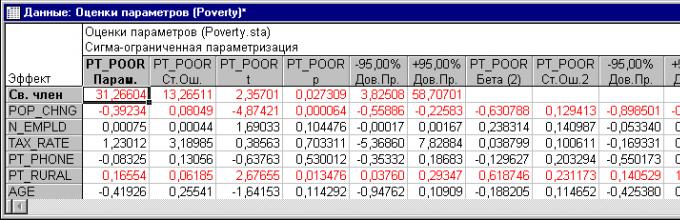
Чтобы узнать, какая из независимых переменных делает больший вклад в предсказание уровня бедности, изучим стандартизованные коэффициенты (или Бета) регрессии.

Рис. 1. Оценки параметров коэффициентов регрессии.

Коэффициенты Бета это коэффициенты, которые вы бы получили, если бы привели все переменные к среднему 0 и стандартному отклонению 1. Следовательно величина этих Бета коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в зависимую переменную. Как видно из Таблицы, показанной выше, переменные изменения населения с 1960 года (POP_ CHING), процент населения, проживающего в деревне (PT_RURAL) и число людей, занятых в сельском хозяйстве (N_Empld) являются самыми главными предикторами уровня бедности, т.к. только они статистически значимы (их 95% доверительный интервал не включает в себя 0). Коэффициент регрессии изменения населения с 1960 года (Pop_Chng) отрицательный, следовательно, чем меньше возрастает численность населения, тем больше семей, которые живут за чертой бедности в соответствующем округе. Коэффициент регрессии для населения (%), проживающего в деревне (Pt_Rural) положительный, т.е., чем больше процент сельских жителей, тем больше уровень бедности.

Значимость эффектов предиктора

Просмотрим Таблицу с критериями значимости.

Рис. 2. Одновременные результаты для каждой заданной переменной.

Как показывает эта Таблица, статистически значимы только эффекты 2 переменных: изменение населения с 1960 года (Pop_Chng) и процент населения, проживающего в деревне (Pt_Rural), p < .05.

Анализ остатков. После подгонки уравнения регрессии, почти всегда нужно проверять предсказанные значения и остатки. Например, большие выбросы могут сильно исказить результаты и привести к ошибочным выводам.

Построчный график выбросов

Обычно необходимо проверять исходные или стандартизованные остатки на большие выбросы.

Рис. 3. Номера наблюдений и остатки.

Шкала вертикальной оси этого графика отложена по величине сигма, т.е., стандартного отклонения остатков. Если одно или несколько наблюдений не попадают в интервал ± 3 умноженное на сигма, то, возможно, стоит исключить эти наблюдения (это можно легко сделать через условия выбора наблюдений) и еще раз запустить анализ, чтобы убедится, что результаты не изменяются этими выбросами.

Расстояния Махаланобиса

Большинство статистических учебников уделяют много времени выбросам и остаткам относительно зависимой переменной. Тем не менее роль выбросов в предикторах часто остается не выявленной. На стороне переменной предиктора имеется список переменных, которые участвуют с различными весами (коэффициенты регрессии) в предсказании зависимой переменной. Можно считать независимые переменные многомерным пространством, в котором можно отложить любое наблюдение. Например, если у вас есть две независимых переменных с равными коэффициентами регрессии, то можно было бы построить диаграмму рассеяния этих двух переменных и поместить каждое наблюдение на этот график. Потом можно было отметить на этом графике среднее значение и вычислить расстояния от каждого наблюдения до этого среднего (так называемый центр тяжести) в двумерном пространстве. В этом и заключается основная идея вычисления расстояния Махаланобиса . Теперь посмотрим на гистограмму переменной изменения населения с 1960 года.

Рис. 4. Гистограмма распределения расстояний Махаланобиса.

Из графика следует, что есть один выброс на расстояниях Махаланобиса.

Рис. 5. Наблюдаемые, предсказанные и значения остатков.

Обратите внимание на то, что округ Shelby (в первой строке) выделяется на фоне остальных округов. Если посмотреть на исходные данные, то вы обнаружите, что в действительности округ Shelby имеет самое большое число людей, занятых в сельском хозяйстве (переменная N_Empld). Возможно, было бы разумным выразить в процентах, а не в абсолютных числах, и в этом случае расстояние Махаланобиса округа Shelby, вероятно, не будет таким большим на фоне других округов. Очевидно, что округ Shelby является выбросом .

Удаленные остатки

Другой очень важной статистикой, которая позволяет оценить серьезность проблемы выбросов, являются удаленные остатки . Это стандартизованные остатки для соответствующих наблюдений, которые получаются при удалении этого наблюдения из анализа. Помните, что процедура множественной регрессии подгоняет поверхность регрессии таким образом, чтобы показать взаимосвязь между зависимой и переменной и предиктором. Если одно наблюдение является выбросом (как округ Shelby), то существует тенденция к "оттягиванию" поверхности регрессии к этому выбросу. В результате, если соответствующее наблюдение удалить, будет получена другая поверхность (и Бета коэффициенты). Следовательно, если удаленные остатки очень сильно отличаются от стандартизованных остатков, то у вас будет повод считать, что регрессионный анализа серьезно искажен соответствующим наблюдением. В этом примере удаленные остатки для округа Shelby показывают, что это выброс, который серьезно искажает анализ. На диаграмме рассеяния явно виден выброс.

Рис. 6. Исходные остатки и Удаленные остатки переменной, означающей процент семей, проживающих ниже прожиточного минимума.

Большинство из них имеет более или менее ясные интерпретации, тем не менее обратимся к нормальным вероятностным графикам.

Как уже было упомянуто, множественная регрессия предполагает, что существует линейная взаимосвязь между переменными в уравнении и нормальное распределение остатков. Если эти предположения нарушены, то вывод может оказаться неточным. Нормальный вероятностный график остатков укажет вам, имеются ли серьезные нарушения этих предположений или нет.

Рис. 7. Нормальный вероятностный график; Исходные остатки.

Этот график был построен следующим образом. Вначале стандартизованные остатки ранжируюся по порядку. По этим рангам можно вычислить z значения (т.е. стандартные значения нормального распределения) на основе предположения, что данные подчиняются нормальному распределению. Эти z значения откладываются по оси y на графике.

Если наблюдаемые остатки (откладываемые по оси x) нормально распределены, то все значения легли бы на прямую линию на графике. На нашем графике все точки лежат очень близко относительно кривой. Если остатки не являются нормально распределенными, то они отклоняются от этой линии. Выбросы также становятся заметными на этом графике.

Если имеется потеря согласия и кажется, что данные образуют явную кривую (например, в форме буквы S) относительно линии, то зависимую переменную можно преобразовать некоторым способом (например, логарифмическое преобразование для "уменьшения" хвоста распределения и т.д.). Обсуждение этого метода находится за пределами этого примера (Neter, Wasserman, и Kutner, 1985, pp. 134-141, представлено обсуждение преобразований, убирающих ненормальность и нелинейность данных). Однако исследователи очень часто просто проводят анализ напрямую без проверки соответствующих предположений, что ведет к ошибочным выводам.

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии

где – зависимая переменная (результативный признак),– независимые, или объясняющие, переменные (признаки-факторы).

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

2.1. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.

    Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.

    Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.

Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.

Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором
факторов, то для нее рассчитывается показатель детерминации
, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии
факторов. Влияние других, не учтенных в модели факторов, оценивается как
с соответствующей остаточной дисперсией.

При дополнительном включении в регрессию
фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:

и
.

Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор
не улучшает модель и практически является лишним фактором.

Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если
. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

Пусть, например, при изучении зависимости
матрица парных коэффициентов корреляции оказалась следующей:

Таблица 2.1

Очевидно, что факторы идублируют друг друга. В анализ целесообразно включить фактор, а не, хотя корреляцияс результатомслабее, чем корреляция факторас
, но зато значительно слабее межфакторная корреляция
. Поэтому в данном случае в уравнение множественной регрессии включаются факторы,.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:

    Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл.

    Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.

Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы
были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных

матрица коэффициентов корреляции между факторами имела бы определитель, равный единице:

.

Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:

.

Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.

Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если
, то возможно построение следующего совмещенного уравнения:

Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по
-критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми.

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

    Метод исключения – отсев факторов из полного его набора.

    Метод включения – дополнительное введение фактора.

    Шаговый регрессионный анализ – исключение ранее введенного фактора.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а
-критерий меньше табличного значения.


Лекция 3. Множественная регрессия

    Условия применения метода и его ограничения

Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономических переменных контролировать нельзя, т.е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии:

Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Требования к факторам:

    Должны быть количественно измеримы. Если необходимо, включить в модель качественный фактор, не имеющий количественного измерения, ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов).

    Не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда

для зависимости

может привести к нежелательным последствиям, повлечь неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель, поэтому параметры уравнения регрессии оказываются неинтерпретированными.

    Мультиколлинеарность

Специфическим для многофакторных систем является условие недопустимости слишком тесной связи между факторными признаками. Это условие часто именуется проблемой коллинеарности факторов. Коллинеарность означает достаточно тесную неслучайную линейную корреляцию одних факторов с другими. Часто рекомендуют исключить фактор, связанный с другим фактором при . Из двух тесно связанных друг с другом факторов рационально исключить фактор, слабее связанный с результативным признаком.

Более сложная методика требуется для нахождения и исключения фактора, не имеющего тесной связи с каким-либо отдельным фактором, но имеющего тесную многофакторную связь с комплексом остальных факторов. Это положение называют мультиколлинеарностью. Для ее измерения следует вычислить последовательно коэффициенты множественной корреляции (или детерминации) каждого фактора (в роли результата) со всеми прочими факторами (в роли объясняющих переменных). Обнаружив мультиколлинеарный фактор либо несколько таковых, следует рассмотреть возможность исключения наиболее зависимого от комплекса остальных фактора, если это не приведет к потере экономического смысла модели.

Коллинеарность и мультиколлинеарность факторов в экономических системах возникают неслучайно. В совокупности однородных предприятий или регионов, как правило, в силу законов экономики возникает параллельная вариация факторных признаков: те предприятия, которые имеют лучшие значения одних факторов, например, лучшие природные условия, одновременно имеют и более высокую фондо- и энерговооруженность, более высокую квалификацию персонала, лучшую технологию и т.п. Отсюда и неизбежная большая или меньшая коллинеарность всех факторов производства либо социально-экономических условий жизни.

Наличие в системе коллинеарности ухудшает математические качества модели, может привести к неустойчивости результативных параметров, резко меняющихся при небольшом изменении значений факторов.

Специфичной проблемой многофакторного анализа является вопрос о возможности замены фактора, по которому отсутствует информация, на другой фактор и последствия такой замены.

Следует по возможности найти другую переменную, значения которой известны и которая находится в достаточно тесной связи с отсутствующим фактором. Например, если нет данных по региону о средней заработной плате, то их можно заменить величиной валового регионального продукта на душу населения, имея в виду, что между этими экономическими признаками должна быть тесная (хотя и неизвестная точно) связь.

Важно учитывать, с какой целью строится модель. Если целью является только прогнозирование результативного признака, то замена фактора другой пременной при ее тесной связи с заменяемым фактором не приведет к существенным ошибкам. Но если целью модели являлось принятие менеджером решений о своей экономической политике, то замена управляемого фактора на тесно с ним связанный, однако неуправляемый заменяющий фактор лишает модель смысла, несмотря на высокую детерминацию.

    Выбор типа многофакторной модели и факторных признаков

Связь результативного признака y с факторами x 1 , x 2 , …, x k выражается уравнением:

(22)

где a – свободный член уравнения;

k – число факторов;

j – номер фактора;

i – номер единицы совокупности;

b j – коэффициент условно-чистой регрессии при факторе x j , измеряющий изменение результата при изменении фактора на его единицу, и при постоянстве прочих факторов, входящих в модель;

ε i – случайная вариация y i , не объясненная моделью.

Модель в форме (22) является аддитивной. Это означает, что в основе модели лежит гипотеза о том, что каждый фактор что-то добавляет или что-то отнимает от значения результативного признака. Такая гипотеза о типе связи причин и следствия вполне отражает ряд экономических систем взаимосвязанных признаков. Например, если y – это урожайность сельскохозяйственной культуры, а x 1 , x 2 , …, x k – агротехнические факторы: дозы разных видов удобрений, число прополок, поливов, доля потерь при уборке, то действительно, каждый из этих факторов либо повышает, либо снижает величину урожайности, причем результат может существовать и без любых из перечисленных факторов.

Однако аддитивная модель пригодна не для любых связей в экономике. Если изучается такая связь как зависимость объема продукции предприятия y от занимаемой площади x 1 , числа работников x 2 , стоимости основных фондов x 3 (или всего капитала), то каждый из факторов является необходимым для существования результата, а не добавлением к нему. В таких ситуациях нужно исходить из гипотезы о мультипликативной форме модели:

(23)

Такая модель по ее первым создателям получила название «модель Кобба-Дугласа».

Возможна и смешанная форма модели, в которой одни факторы будут входить аддитивно, а другие мультипликативно.

При выборе факторных признаков следует исходить из следующих положений.

    Факторы должны являться причинами, а результативный признак – их следствием. Недопустимо в число факторов включать признак, занимающий в реальной экономике место на «выходе» системы, т.е. зависимый от моделируемого. Например, строится модель себестоимости центнера зерна. Факторами взяты урожайность зерновых культур и трудоемкость центнера, но коэффициент детерминации невелик, модель плохая. Для ее «улучшения» в число факторов добавили рентабельность производства зерна. Коэффициент детерминации сразу подскочил до 0,88. Но модель не стала лучше, она стала бессмысленной, так как рентабельность зависит от себестоимости, а не наоборот.

    Факторный признаки не должны быть составными частями результативного признака. В ту же модель себестоимости нельзя вводить факторами зарплату в расчете на центнер зерна, затраты на перевозку центнера зерна и т.п. связь целого с ее структурными частями следует анализировать не с помощью корреляционного анализа, а с помощью систем индексов.

    Следует избегать дублирования факторов. Каждый реальный фактор должен быть представлен одним показателем. Например, трудовой фактор в модели объема продукции может быть представлен либо среднесписочным числом работников, либо затратами человеко-дней (человеко-часов) на производство продукции, но не обоими показателями. Дублирование факторов ведет к раздроблению влияния фактора, и он может оказаться ненадежным из-за такого раздробления.

    Следует по возможности избегать факторов, тесно связанных с другими.

    Следует включать факторы одного уровня иерархии, не следует включать и факторы вышележащего уровня и их субфакторы. Например, в модель себестоимости зерна включаем урожайность, трудоемкость, но не добавляем еще балл плодородия, дозу удобрений, энерговооруженность работников, т.е. субфакторы – причины, влияющие на урожайность и трудоемкость. Включение субфакторов тоже дублирование фактора.

    Есть логика в таком построении модели, при котором все признаки отнесены на одну и ту же единицу совокупности, как результативный признак, так и факторы. Например, если моделируется объем продукции предприятия, то и факторы должны относиться к предприятию: число работников, площадь угодий, основные фонды и т.д. Если строится модель заработной платы работника, то и факторы должны относиться к работнику: его стаж, возраст, образование, разряд тарифной сетки (шкалы), энерговооруженность и т.д.

    Действует принцип простоты модели. Если возможно построить хорошую модель с пятью факторами, то не следует гнаться за идеальной моделью с десятью факторами, обычно лишние факторы ухудшают модель.

    Системы показателей многофакторной корреляции и регрессии

Рассмотрим данную систему показателей на примере связи урожайности зерновых культур в 51 агрофирме Орловской области. Первоначально были отобраны 8 факторных признаков, которые могут влиять на вариацию урожайности:

x 1 – размер посевной площади зерновых, га;

x 2 – удельный вес зерновых в общей площади, %;

x 3 – затраты на 1 га посева зерновых, тыс. руб./га;

x 4 – затраты труда на 1 га, чел.-ч;.

x 5 – уровень оплаты труда, руб./чел.-ч.;

x 6 – энергообеспеченность, л.с./100 га пашни;

x 7 – число комбайнов на 1000 га зерновых, шт.;

x 8 – число трактористов-машинистов на 100 га пашни, чел.

Первоначальное уравнение регрессии имеет вид:

Однако надежно отличными от нуля оказались только коэффициенты при x 3 (t -критерий равен 10,5) и при x 8 (t -критерий равен 2,72). Большую надежность, чем другие факторы имеет и x 5 .

После отсева ненадежных факторов, т.е. исключения их из уравнения, окончательное уравнение регрессии таково:

Таким образом, на различие урожайности в данных 51 агрофирмы сильнее всего и надежно повлияли различия между предприятиями в затратах на 1 га, в уровне оплаты труда и в обеспеченности квалифицированными работниками.

Каждый из коэффициентов, называемых коэффициентами чистой регрессии, интерпретируются как величина изменения урожайности при условии, что данный фактор изменяется на принятую единицу измерения, а два других фактора остаются постоянными на средних уровнях. Например, b 3 означает, что при увеличении затрат на 1 га зерновых и при неизменности оплаты труда и обеспеченности трактористами-машинистами урожайность в среднем увеличивалась в среднем на 4, 6 ц/га. Термин «условно чистая регрессия» означает, что влияние отдельного фактора очищено от сопутствующей вариации только тех факторов, которые входят в уравнение, но не очищено от возможной сопутствующей вариации других факторов.

Величина коэффициентов условно чистой регрессии зависит от принятых единиц измерения. Если бы фактор x 3 измерялся не в тысячах рублей на гектар, а в рублях на гектар, то коэффициент b 3 был бы равен 0,00461 руб./га. Следовательно, сравнивать между собой коэффициенты условно чистой регрессии нельзя. Чтобы получить сравнимые коэффициенты влияния вариации факторов на вариацию результата, следует избавиться от единиц измерения, привести к одной условной единице. Для этого можно применить два способа.

Первый способ называется стандартизацией. Этот термин возник из английского названия среднего квадратического отклонения (Standard deviation). Стандартизированные коэффициенты регрессии выражаются в долях или величинах, если они превышают единицу – в величинах σ y . Стандартизированные коэффициенты обозначают греческой буквой β и называют бета-коэффициентами. Их формула такая:

В нашем примере получаем:

β 3 = 0,772;

β 5 = 0,147;

β 8 = 0,223.

Интерпретация бета-коэффициентов такова: при изменении фактора x 3 на одно его среднее квадратическое отклонение от средней величины и при постоянстве других факторов результативный признак (урожайность) отклонится от своего среднего уровня на 0,772 его среднего квадратического отклонения. Так как все стандартизированные коэффициенты выражены в одинаковых единицах измерения, в σ y , они сравнимы между собой, и можно сделать вывод, что на вариацию урожайности сильнее всего повлияла в изучаемой совокупности предприятий вариация затрат на гектар посева.

Другой способ приведения коэффициентов регрессии к сравнимому виду – их преобразование в коэффициенты эластичности. Формула коэффициента эластичности ℓ j :

(25)

Интерпретируется коэффициент эластичности следующим образом: при изменении фактора x j на его среднюю величину и при постоянстве других входящих в уравнение факторов результативный признак в среднем изменится на ℓ j части его средней величины (или на ℓ j средних, если ℓ j >1, что бывает реже). Часто говорят, «изменится на ℓ j процентов на 1% изменения фактора».

В нашем примере имеем:

Коэффициенты эластичности так же выражены, как и β j , в одинаковых единицах и сравнимы между собой. Ими удобнее, чем β-коэффициентами, пользоваться в планировании и прогнозировании. Вряд ли менеджер станет планировать увеличение фактора, скажем, инвестиций на 0,6 сигмы. Обычно планируют изменение факторов, если они управляемы, на столько-то процентов от достигнутого уровня. Например, если планируем увеличить затраты на гектар зерновых на 10%, оплату труда на 30%, а обеспеченность квалифицированными трактористами-машинистами на 20%, то можно ожидать изменения урожайности на
, где k j – планируемые темпы прироста факторов.

Теперь рассмотрим систему показателей тесноты многофакторных связей. Прежде всего строится матрица парных коэффициентов корреляции (табл. 1).

Таблица 1. Матрица парных коэффициентов корреляции

Признаки

x 3

x 5

x 8

x 3

x 5

x 8

Матрица парных коэффициентов корреляции дает исходные данные для других показателей тесноты связи и для первичной проверки на коллинеарность. В данном случае все связи между факторами слабые, коллинеарность не испортит модель.

Важнейшим показателем тесноты связи в многофакторной системе является коэффициент множественной детерминации R 2 . Он измеряет общую тесноту связи вариации результативного признака y с вариацией всей системы входящих в модель факторов. Величина коэффициента множественной детерминации может быть вычислена несколькими способами.

1.Вычисление на основе матрицы парных коэффициентов корреляции

,

где Δ * - определитель матрицы;

, (26)

а Δ – определитель матрицы, не включающей первой строки Δ * и ее последнего столбца, т.е.:

При двух факторах получается упрощенная формула расчета:

(27)

Из (27) следует, что при независимости факторов друг от друга, т.е. , коэффициент множественной детерминации есть сумма парных коэффициентов детерминации.

Пользуясь формулой (27), можно вычислить три возможных двухфакторных коэффициента детерминации:

2.Вычисление на основе парных коэффициентов корреляции и β-коэффициентов:

В примере: R 2 =0,86·0,772+0,35·0,147+0,433·0,223=0,8119.

3.Вычисление как корреляционное отношение, т.е. отношение вариации результативного признака y , связанной с вариацией системы факторов, входящих в модель (в уравнение регрессии), ко всей, общей, вариации результативного признака:

. (30)

Числитель формулы (30) – это сумма квадратов отклонений индивидуальных расчетных значений результативного признака от его средней, а знаменатель – сумма квадратов фактических значений результативного признака от средней, для всех единиц совокупности.

Частными коэффициентами детерминации называются показатели, измеряющие, на какую долю уменьшается необъясненная вариация уже имеющимися в модели факторами при включении в модель данного фактора x m . Формула частного коэффициента детерминации такова:

В нашем примере:

Интерпретация такова: включение в модель фактора x 3 после x 5 и x 8 y на 74%; включение фактора x 5 после x 3 и x 8 уменьшает необъясненную вариацию y на 10%; включение фактора x 8 после x 3 и x 5 уменьшает необъясненную вариацию y на 20%.

Коэффициенты частной детерминации несравнимы между собой, так как это доли разных величин-знаменателей.

Извлекая корень квадратный из любого коэффициента детерминации, получают коэффициент соответствующей корреляции: множественной, парной или частной.

5. Включение в многофакторную модель неколичественных факторов

Неколичественными являются такие факторы аграрного производства, как природная зона, форма собственности предприятий, преобладающее производственное направление (отрасль) и другие. Предпочтительно не смешивать в исходной совокупности предприятия или регионы, различающиеся по этим качественным признакам. Но может возникнуть и необходимость построения модели с неоднородными единицами совокупности, например, если число единиц, однородных по качественному признаку, слишком мало для надежной связи. Иногда может быть поставлена цель измерения чистого влияния неколичественного фактора, например, формы собственности на результаты производства, а это требует включения качественного фактора в многофакторную модель.

В таких случаях качественные градации признака можно закодировать специальными переменными, часто называемыми «фиктивными» или «структурными» переменными. Они отражают неоднородность качественной структуры совокупности. Предположим, необходимо построить регрессионную модель рентабельности продукции предприятий, причем в регионе имеется 16 государственных предприятий, 28 частных, 13 кооперативной формы собственности.

Если игнорировать различия, связанные с формой собственности, то они или уйдут в остаточную вариацию, ухудшив модель рентабельности, либо в неизвестной пропорции станут смешиваться с влиянием тех или иных качественных факторов, искажая меру их влияния.

Необходимо для m неколичественных факторов или градаций такового фактора ввести m -1 структурную переменную, обозначим которую U j . Данные для расчета будут иметь следующий вид при m =3 (табл. 2).

Таблица 2. Исходные данные со структурными переменными

Форма собственности

Единица совокупности

Количественные признаки

Структурные переменные

X 1

X 2

X k

U 1

U 2

Государственная

Значения этих признаков

Значения этих признаков

Кооперативная

Значения этих признаков

В результате решения будет получена модель вида:

где x k +1 соответствуют переменной U 1 , а x k +2 – переменной U 2 .

Перепишем модель в специальных обозначениях:

Значение коэффициентов при структурных переменных таково: коэффициент c 1 означает, что предприятия частной формы собственности при тех же значениях количественных факторов x 1 … x k имеют рентабельность на c 1 больше, чем государственные предприятия, которые приняты за базу сравнения (не имеют структурных переменных U 1 и U 2 ). Предприятия кооперативной формы собственности имеют рентабельность на c 2 большую, чем государственные. Величины c 1 и c 2 могут быть как положительными, так и отрицательными.

Вместо общей модели можно записать три частные модели для предприятий отдельных групп по формам собственности, присоединяя коэффициент при структурной переменной к свободному члену уравнения:

а) для предприятий государственного сектора

б) для предприятий частного сектора

в) для предприятий кооперативного сектора

6.Применение многофакторных регрессионных моделей для анализа деятельности предприятий и прогнозирования

Оценка деятельности на основе регрессионной модели в сравнении с простейшим приемом такой оценки – сравнением результата, достигнутого данным предприятием, со средним результатом по однородной совокупности – дает дополнительные преимущества.

Согласно нашему примеру, средняя урожайность по 51 агрофирме составила 22,9 ц/га зерна.

Агрофирма 1 получила 17,6 ц/га. Следовательно, эта фирма отстающая. Однако возникает вопрос: может быть и условия производства у этой фирме были хуже средних? Сравнение со средней по совокупности полностью игнорирует различие в «факторообеспеченности» предприятий, а на самом деле предприятия всегда находятся не в одинаковых условиях.

Оценка деятельности на основе регрессионной модели предполагает учет неравенства условий производства, например, плодородия почв, финансового положения, наличия квалифицированных кадров и другие. Полностью учесть различие в условиях производства между предприятиями невозможно, так как любая модель учитывает не все факторы вариации урожайности. Оценка на основе модели производится сравнением фактического результата (урожайности) с тем результатом, который был бы достигнут предприятием при фактически имеющихся факторах и средней по совокупности их эффективности, выраженной коэффициентами условно чистой регрессии. Рассмотрим результаты расчета урожайности двух фирм (табл. 3).

Таблица 3. Фактический и расчетный результат производства

Агрофирма

Факторные признаки

Урожайность, ц/га

x 3

x 5

x 8

фактическая

расчетная

Средняя по выборке

Обе фирмы имеют худшие, чем в среднем в выборке, значения основных факторов x 3 и x 8 , а соответственно и значения расчетной урожайности ниже, чем средняя. Но при этом фирма 1 практически имеет ту же расчетную урожайность, что и фактически полученную. Нет основания считать эту фирму отстающей. Фирма 2 имеет фактическую урожайность ниже, чем расчетная по имеющимся факторам. Это означает, что либо у этой фирмы оказались хуже среднего неизвестные, не входящие в модель факторы, либо степень использования основных факторов – затрат на гектар и обеспеченность квалифицированными работниками ниже, чем в среднем.

Прогнозирование на основе регрессионной модели исходит из предположения, что факторы управляемы и могут принять то или иное плановое, ожидаемое значение, а прочие неизвестные условия сохранятся на среднем по совокупности уровне. Управляемость факторов не означает, что при прогнозе в модель можно подставлять любые их значения. Уравнение регрессии отражает те условия, которые существовали в совокупности, по данным которой уравнение получено. Если бы значения факторных признаков были в 2-3 раза более высокими, то нельзя утверждать, что коэффициенты условно чистой регрессии остались бы теми же.

Поэтому рекомендуется при прогнозировании по уравнению регрессии не выходить за пределы реально наблюдаемых значений факторов в совокупности или выходить за эти границы не более чем на 10-15% средних величин. Не менее важным требованием при прогнозировании является требование о соблюдении системности прогнозируемых значений факторов. Необходимо учитывать знак и тесноту связи между факторами. Например, если прогнозируется повысить степень обеспеченности квалифицированными работниками, то нельзя оставить без изменения, тем более снижать, прогнозируемую величину уровня оплаты труда. Планируя рост энерговооруженности, необходимо примерно в той же пропорции увеличить и фондовооруженность.

Ориентируясь на указанные в таблице 3 значения факторов, предположим, что прогнозируя урожайность, планируем затраты на гектар (x 3 ) на уровне 3 тыс. руб., наличие трактористов-машинистов на 100 га пашни 0,8; оплату часа труда в размере 20 руб. в час. Подставляя эти значения в регрессионную модель получим точечный прогноз урожайности зерновых культур:

Точечный прогноз представляет собой математическое ожидание (среднюю) возможных с разной вероятностью значений прогнозируемого признака. Необходимо дополнить точечный прогноз расчетом доверительных границ с достаточно большой вероятностью. Для этого следует использовать величину средней квадратической ошибки аппроксимации, которая вычисляется по формуле:

(33)

Числитель подкоренного выражения – это остаточная, не объясненная моделью сумма квадратов отклонений результативного признака, а знаменатель – число степеней свободы остаточной вариации. В нашем примере остаточная сумма квадратов отклонений равна 814,3. Имеем:

Следовательно, с надежностью 0,95 прогнозируемая урожайность составит 25,4±4,16·2, или от 17,8 до 33,72 ц/га. Все эти расчеты относятся к прогнозам урожайности для отдельных агрофирм. Если речь идет о средней урожайности по совокупности 51 агрофирмы, то средняя ошибка средней арифметической величины равна среднему квадратическому отклонению, деленному на корень квадратный из объема выборки n , т.е. составит:

Интерпретация этого значения ошибки прогноза средней величины такова: если обеспечить 51 агрофирму факторами x 3 , x 5 , x 8 на уровнях соответственно 3, 20, 0,8, то будет получена средняя по совокупности урожайность 25,4±0,583 ц/га. С вероятностью 0,95 средняя по совокупности ожидаемая урожайность составит 25,4±0,583·2, или от 23,7 до 27,1 ц/га.

Эконометрической корреляционно-регрессионной моделью системы взаимосвязанных признаков изучаемой совокупности является такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака в совокупности, обладает высоким значением коэффициента детерминации (не ниже 0,5), надежными и правильно интерпретируемыми в соответствии (по знаку и по порядку величины) с теорией изучаемой системы коэффициентами регрессии, и в силу данных свойств пригодное для оценки деятельности единиц совокупности и для прогнозирования.

Множественной регрессии (2)Реферат >> Маркетинг

Вводя их в модель, т.е, построить уравнение множественной регрессии . Множественная регрессия широко используется в решении проблем спроса...

Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости переменной у от нескольких объясняющих переменных (х 1, х 2 ,…, х k) которая может быть решена с помощью множественного корреляционно-регрессионного анализа.

При исследовании зависимости методами множественной регрессии задача формируется так же, как и при использовании парной регрессии, т.е. требуется определить аналитическое выражение формы связи между результативным признаком у и факторными признаками х, х 2 , ..., х k , найти функцию , где k – число факторных признаков

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Из-за особенностей метода наименьших квадратов во множественной регрессии, как и в парной, применяются только линейные уравнения и уравнения, приводимые к линейному виду путем преобразования переменных. Чаще всего используется линейное уравнение, которое можно записать следующим образом:

a 0 , a 1, …, a k – параметры модели (коэффициенты регрессии);

ε j – случайная величина (величина остатка).

Коэффициент регрессии а j показывает, на какую величину в среднем изменится результативный признак у, если переменную х j увеличить на единицу измерения при фиксированном (постоянном) значении других факторов, входящих в уравнение регрессии. Параметры при x называются коэффициентами «чистой» регрессии .

Пример.

Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:

y – расходы семьи за месяц на продукты питания, тыс. руб.;

x 1 – месячный доход на одного члена семьи, тыс. руб.;

x 2 – размер семьи, человек.

Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Первый параметр не подлежит экономической интерпретации.

Оценивание достоверности каждого из параметров модели осуществляется при помощи t-критерия Стьюдента. Для любого из параметров модели а j значение t-критерия рассчитывается по формуле , где


S ε – стандартное (среднее квадратическое) отклонение уравнения регрессии)

определяется по формуле

Коэффициент регрессии а j считается достаточно надежным, если расчетное значение t- критерия с (n - k - 1 ) степенями свободы превышает табличное, т.е. t расч > t а jn - k -1 . Если надеж­ность коэффициента регрессии не подтверждается, то следует; вывод о несущественности в модели факторного j признака и необходимости его устранения из модели или замены на другой факторный признак.

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставлять факторные признаки по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий применяются частные коэффициенты эластичности Э j и бета-коэффициенты β j .

Формула для расчета коэффициента эластичности

где

a j – коэффициент регрессии фактора j ,

Среднее значение результативного признака

Среднее значение признака j

Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная у при изменении фактора j на 1 %.

Формула определения бета - коэффициента.

, где

S xj – среднее квадратическое отклонение фактора j ;

S y - среднее квадратическое отклонение фактора y.

β - коэффициент показывает, на какую часть величины среднего квадратического отклонения S y из­менится зависимая переменная у с изменением со­ответствующей независимой переменной х j на величину своего среднего квадратического отклонения при фиксированном значении остальных неза­висимых переменных.

Долю влияния определенного фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов Δ j .

Указанные коэффициенты позволяют проранжировать факторы по степени влияния факторов на зависимую переменную.

Формула определения дельта - коэффициента.

r yj – коэффициент парной корреляции между фактором j и зависимой переменной;

R 2 – множественный коэффициент детерминации.

Коэффициент множественной детерминации используют для оценки качества множественных регрессионных моделей.

Формула определения коэффициента множественной детерминации.

Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием факторных признаков, т.е. опре­деляет, какая доля вариации признака у учтена в модели и обусловлена влиянием на него факторов, включенных в модель. Чем ближе R 2 к единице, тем выше качество модели

При добавлении независимых переменных значение R 2 уве­личивается, поэтому коэффициент R 2 должен быть скорректи­рован с учетом числа независимых переменных по формуле

Для проверки значимости модели регрессии используется F-критерий Фишера. Он определяется по формуле

Если расчетное значение критерия с γ 1 , = k и γ 2 = (n - k- 1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

В качестве меры точностимодели применяют стандартную ошибку, которая представляет собой отношение суммы квадратов уровней остаточной компоненты к величине (n - k -1):

Классический подход к оцениванию параметров линейной модели основан на методе наименьших квадратов (МНК) . Система нормальных уравнений имеет вид:

Решение системы может быть осуществлено по одному из известных способов: Метод Гаусса, метод Крамера и т.д.

Пример15.

По четырем предприятиям региона (таблица 41) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%). Требуется написать уравнение множественной регрессии.

Таблица 41 – Зависимость выработки продукции на одного работника

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них - уравнение регрессии - рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х - независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая - зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии - это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х 1 , х 2 ...х с)+E. В данной ситуации у выступает зависимой переменной, а х - объясняющей. Переменная Е - стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная - это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е - стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный - о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 - тем сильнее связь между параметрами, чем ближе к 0 - тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого - вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель - свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х - нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y - тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x 1 ,x 2 ,…,x m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а 0 + a 1 х 1 + а 2 х 2 ,+ ... + a m x m . При этом а2, a m , считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах 1 b1 х 2 b2 ...x m bm . В данном случае показатели b 1 , b 2 ..... b m - называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

  • Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
  • Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям - система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
  • В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

  • Способ исключения.
  • Способ включения.
  • Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий - отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.