«Моё имя будет оболгано, мне припишут множество злодеяний. Мировой сионизм всеми силами будет стремиться уничтожить наш Союз, чтобы Россия никогда уже не смогла подняться. Острие борьбы будет направлено на отрыв окраин от России. С особой силой поднимет голову национализм. Появится много вождей-пигмеев, предателей внутри своих наций…»

«Сталин есть центр, сердце всего того, что лучами расходится от Москвы по всему миру».

Французский писатель А. Барбюс

65 лет назад, 5 марта 1953 года, ушел из жизни великий народный вождь Иосиф Сталин. Человек, который смог возродить русскую империю в виде Советского Союза, победившего во Второй мировой войне, создавший мощные вооруженные силы, ядерный щит нашей Родины, лучшую в мире науку и образование.

В «демократической России», созданной в 1991-1993 гг., его объявили маньяком и кровавым диктатором. Почему Сталина так ненавидят различные западники, либералы и местечковые националисты? Ответ прост. Сталин был настоящим народным вождём, который всю жизнь отдал на решение глобальных и национальных задач русской цивилизации и русского народа. Он заставил служить Родине не щадя себя правительство и коммунистическую партию. А после смерти не оставил ни богатств, ни счетов в заграничных банках, ни дворцов и вилл, ни ворованных миллиардов и золота. Его сокровищем стала советская сверхдержава.

Самое главное: Сталин показал магистральный путь будущей великой России (СССР) и всего человечества – общество «золотого века», общество социальной справедливости, служения и созидания. Общество, где господствует этика совести, а человек является созидателем, творцом, служит Родине и народу. Сталин показал альтернативный путь развития всего человечества. Хозяева западного проекта и цивилизации строят несправедливый мировой порядок – глобальную невольничью, рабовладельческую, кастовую цивилизацию, где есть кучка «хозяев жизни и денег», «избранных» которым позволено всё, и которые имеют доступ к подлинному знанию, самым передовым достижениям науки, техники, медицины.

А остальная масса людей погружена в мрак нищеты, не имеет доступа к нормальному образованию и здравоохранению, постоянно одурманивается различными наркотиками: табаком, алкоголем, более тяжелыми дурманами, пищевыми суррогатами, информационно-виртуальными иллюзиями и т. д. Их срок жизни сознательно сокращается, духовность, интеллект и физическое состояние подавляются, опускаются на уровень двуногих орудий, скота.

При этом западные «элиты» постоянно разрабатывают и претворяют в жизнь планы по сокращению человеческой «биомассы». Чтобы больше ресурсов осталось «избранным», чтобы можно было создать чистенькую планету, без двуногих «вирусов», убивающих Землю.

Это и вредная пища, и подсаживание людей на лекарства, с подавлением нормального иммунитета и отсутствием нормальных программ по физическому и духовному развитию людей. Это создание общества стресса, где люди вертятся как белки в колесе добывая ресурсы для «нормальной» жизни, но в реальности гробят психическое и физическое здоровье, подсаживаются на стимуляторы и дурманы, чтобы временно забыться. Это и общество потребления, которая губит как планету, её биосферу, так и самого человека, как часть общей живой системы. Человека превращают в животное-потребителя, полностью зависимое от «хозяев жизни». Это и система, направленная на разрушение воспроизводства человечества – пропаганда абортов, противозачаточных средств, идей бездетности, гомосексуальных «браков», различных извращений (извращенцы детей не рожают), виртуальный секс, на очереди секс-роботы и т. д.

При Сталине в СССР стали строить справедливое государство и общество, общество служения и созидания, общество с господством этики совести. Отсюда мощнейший духовный народный порыв, который позволил не только создать сверхдержаву, победить в самой страшной в истории человечества войне, но и ликвидировать все последствия жесточайшей мировой бойни, создать социалистический лагерь, что позволяло противостоять западному миру, опирающемуся на свои колонии и полуколонии. Народная поддержка позволила построить самостоятельное народное хозяйство, снабжавшее всем необходимым советских людей и даже поддерживать союзников, создать лучшие в мире вооруженные силы, исключив угрозу нового открытого масштабного нападения на СССР-Россию на несколько поколений (большая часть жителей России живет в мире только благодаря этому фундаменту), создать лучшие в мире науку, образование, систему, раскрывающую творческий, созидательный потенциал детей и молодежи и многое другое.

Простой народ при жизни Иосифа Виссарионовича его боготворил. О нём пели песни, ставили ему памятники, его имя присваивали городам и крупным предприятиям. Сталин и его правительство приняли разрушенную и разорённую Россию, которая прошла через катастрофу прежнего проекта развития в 1917 году. Большевики (русские коммунисты), вопреки распространенному мнению, к этой катастрофе отношения практически не имели, они уже просто взяли власть в погибшей «старой России». Предложили народу новый проект – советскую цивилизацию, который был в интересах подавляющей части народа. Сумели создать советскую сверхдержаву – вернули большую часть утраченных в годы смуты земель, победили Японию и Германию, которым проиграла царская Россия. Советский Союз включил в свою сферу влияния половину планеты, включая Китай. За годы правления Сталина было перестроено народное хозяйство, ставшее более эффективным, чем у стран лидеров капиталистического мира, создали передовые отрасли промышленности, которые имели только самые передовые державы – самолетостроение, кораблестроение, машиностроение, станкостроение, химпром, ВПК, ракетостроение. Создали ядерное оружие и создали фундамент космической отрасли. Ликвидировали безработицу, образование и здравоохранение стали бесплатными и общедоступными. Дети из бедных крестьянских семей, которые не имели никаких шансов при капитализме, становились при социализме профессорами и маршалами, летчиками-асами и министрами.

Под руководством Сталина была выиграна Вторая мировая война, когда хозяева Запада позволили взять власть в Европе немецким нацистам во главе с Гитлером. Хозяева Запада испугались советского проекта. Россия становилась альтернативным центром нового справедливого мирового порядка. Симпатии значительной части человечества, лучших людей Земли были на стороне «солнечной» советской цивилизации. В результате, по сути, был создан «Евросоюз» во главе с Германией и вся его мощь – военно-техническая, демографическая и экономическая была брошена против советской цивилизации, которая бросила вызов господству Запада над планетой. Однако русская (советская) армия разгромила сильного и жестокого врага. Восточная и часть Центральной Европы, включая Восточную Германию, вошла в сферу влияния Москвы. Советский Союз разгромил милитаристскую Японию, взяв реванш за позор Русско-японской войны 1904-1905 гг. и восстановив своё влияние на Дальнем Востоке. С нашей помощью в Китае победили коммунисты и Поднебесная признала СССР «старшим братом».

Сталин не дрогнул перед атомной угрозой со стороны США, которые провели кровавое «испытание» ядерного оружия в Японии. Москва имела настолько мощные вооруженные силы, что США и Англия с союзниками не решились сразу же после завершения Второй мировой войны, начать «горячую» Третью мировую войну (хотя планы были). Вскоре Москва создала свою атомную бомбу и быстрыми темпами создала первоклассный ядерный арсенал. Запад начал «холодную» Третью мировую войну – информационно-идеологическую, экономическую, тайную войну спецслужб, войну на территории других стран (Корейская война и т. д.).

Поэтому наши враги на Западе и российские западники, предавшие СССР и идеалы социализма, социальной справедливости, и ненавидят Сталина. Они создали массу черных мифов, чтобы оболгать великого народного вождя. Однако правда находит дорогу даже в атмосфере тотальной лжи. Поэтому образ Сталина в настоящее время снова популярен в русском народе. В годы его правления у людей была вера в социальную справедливость, в будущее народа и страны. Был создан мощный хозяйственный, научно-технический, образовательный, культурный и военный фундамент, который позволил России дожить до настоящего дня.

Даже откровенный враг Союза и непримиримый антикоммунист, знаменитый британский премьер-министр У. Черчилль, выступая в палате общин 21 декабря 1959 года, в день 80-летия Сталина, признал его выдающуюся роль в мире: «Он был самой выдающейся личностью, импонирующей нашему изменчивому и жестокому времени того периода, в котором проходила его жизнь. Сталин был человеком необычайной энергии и несгибаемой силы воли, резким, жестоким, беспощадным в беседе, которому даже я, воспитанный здесь, в британском парламенте, не мог ничего противопоставить. Сталин прежде всего обладал большим чувством юмора и сарказма и способностью точно воспринимать мысли. Эта сила была настолько велика в Сталине, что он казался неповторимым среди руководителей всех времен и народов. Сталин произвел на нас величайшее впечатление. Он обладал глубокой, лишенной всякой паники, логически осмысленной мудростью. Он был непревзойдённым мастером находить в трудные моменты пути выход из самого безвыходного положения. Кроме того, Сталин в самые критические моменты, а также в моменты торжества был одинаково сдержан и никогда не поддавался иллюзиям».

Куб, шар, пирамида, цилиндр, конус - геометрические тела. Среди них выделяют многогранники. Многогранником называют геометрическое тело, поверхность которого состоит из конечного числа многоугольников. Каждый из этих многоугольников называется гранью многогранника, стороны и вершины этих многоугольников - соответственно ребрами и вершинами многогранника.

Двугранные углы между соседними гранями, т.е. гранями, име­ющими общую сторону - ребро многогранника - являются так­же и двугранными умами многогранника. Углы многоугольников - граней выпуклого многоугольника - являются плоскими умами многогранника. Кроме плоских и двугранных углов у выпуклого многогранника имеются еще и многогранные углы. Эти углы образу­ют грани, имеющие общую вершину.

Среди многогранников различают призмы и пирамиды.

Призма - это многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов, имеющих об­щие стороны с каждым из оснований.

Два равных многоугольника называются основаниями ггризмьг, а параллелограммы - ее боковыми гранями. Боковые грани образуют боковую поверхность призмы. Ребра, не лежащие в основаниях, называются боковыми ребрами призмы.

Призму называют п-угольной, если ее основаниями являются я-угольники. На рис. 24.6 изображена четырехугольная призма АВСDА"В"С"D".

Призму называют прямой, если ее боковыми гранями являются прямоугольники (рис. 24.7).

Призму называют правильной , если она прямая, а ее основа­ния - правильные многоугольники.

Четырехугольную призму называют параллелепипедом , если ее основания - параллелограммы.

Параллелепипед называют прямоугольным, если все его грани - прямоугольники.

Диагональ параллелепипеда - это отрезок, соединяющий его противоположные вершины. У параллелепипеда четыре диаго­нали.

Доказано, что диагонали параллелепи­педа пересекаются в одной точке и делятся этой точкой пополам. Диагонали прямо­угольного параллелепипеда равны.

Пирамида - это многогранник, по­верхность которого состоит из много­угольника - основания пирамиды, и треугольников, имеющих общую верши­ну, называемых боковыми гранями пи­рамиды. Общая вершина этих треуголь­ников называется вершиной пирамиды, ребра, выходящие из вер­шины, - боковыми ребрами пирамиды.

Перпендикуляр, опущенный из вершины пирамиды на основа­ние, а также длина этого перпендикуляра называется высотой пи­рамиды.

Простейшая пирамида - треугольная или тетраэдр (рис. 24.8). Особенность треугольной пирамиды состоит в том, что любую грань можно рассматривать как основание.

Пирамиду называют правильной, если в основании ее лежит правильный многоугольник, а все боковые ребра равны между собой.

Заметим, что следует различать правильный тетраэдр (т.е. тетра­эдр, у которого все ребра равны между собой) и правильную тре­угольную пирамиду (в ее основании лежит правильный треуголь­ник, а боковые ребра равны между собой, но их длина может от­личаться от длины стороны треугольника, который является ос­нованием призмы).

Различают выпуюше и невыпуклые многогранники. Определить вы­пуклый многогранник можно, если воспользоваться понятием вы­пуклого геометрического тела: многогранник называют выпуклым. если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок.

Можно определить выпуклый многогранник иначе: многогран­ник называют выпуклым, если он полностью лежит по одну сторо­ну от каждого из ограничивающих его многоугольников.

Данные определения равносильны. Доказательство этого факта не приво­дим.

Все многогранники, которые до сих пор рассматривались, были выпуклыми (куб, параллелепипед, призма, пирамида и др.). Многогранник, изображенный на рис. 24.9, выпуклым не является.

Доказано, что в выпуклом многогран­нике все грани являются выпуклыми многоугольниками.

Рассмотрим несколько выпуклых многогранников (таблица 24.1)

Из этой таблицы следует, что для всех рассмотренных выпук­лых многогранников имеет место равенство В - Р + Г = 2. Оказа­лось, что оно справедливо и для любого выпуклого многогранни­ка. Впервые это свойство было доказано Л.Эйлером и получило название теоремы Эйлера.

Выпуклый многогранник называют правильным, если его гра­нями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число граней.

Используя свойство выпуклого многогранного угла, можно до­казать, что различных видов правильных многогранников существу­ет не более пяти.

Действительно, если фан и многогранника - правильные тре­угольники, то в одной вершине их может сходиться 3, 4 и 5, так как 60" 3 < 360°, 60° - 4 < 360°, 60° 5 < 360°, но 60° 6 = 360°.

Если в каждой вершине многофанника сходится три правиль­ных треугольника, то получаем правшш/ый тетраэдр, что в пере­воде с феческого означает «четырехгранник» (рис. 24.10, а).

Если в каждой вершине многогранника сходится четыре пра­вильных треугольника, то получаем октаэдр (рис. 24.10, в). Его поверхность состоит из восьми правильных треугольников.

Если в каждой вершине многогранника сходится пято правиль­ных треугольников, то получаем икосаэдр (рис. 24.10, г). Его поверх­ность состоит из двадцати правильных треугольников.

Если грани многофанника - квадраты, то в одной вершине их может сходиться только три, так как 90° 3 < 360°, но 90° 4 = 360°. Этому условию удовлетворяет только куб. Куб имеет шесть фаней и поэтому называется также гексаэдром (рис. 24.10, б).

Если граани многофанника - правильные пятиугольники, то в одной вершине их может сходиться только фи, так как 108° 3 < 360°, пятиугольники и в каждой вершине сходится три грани, называется додекаэдром (рис. 24.10, д). Его поверхность состоит из двенадцати правильных пятиугольников.

Шестиугольными и более грани многогранника не могут быть, так как даже для шестиугольника 120° 3 = 360°.

В геометрии доказано, что в трехмерном евклидовом простран­стве существует ровно пять различных видов правильных много­гранников’.

Чтобы изготовить модель многогранника, нужно сделать его развертку (точнее развертку его поверхности).

Развертка многогранника - это фигура на плоскости, которая получается, если поверхность многогранника разрезать но некото рым ребрам и развернуть ее так, чтобы все многоугольники, вхо­дящие в эту поверхность, лежали в одной плоскости.

Отметим, что многогранник может иметь несколько различных разверток в зависимости от того, какие ребра мы разрезали. На рисунке 24.11 показаны фиг"уры, которые являются различными развертками правильной четырехугольной пирамиды, т.е. пирами­ды, в основании которой лежит квадрат, а все боковые ребра рав­ны между собой.

Чтобы фигура на плоскости была разверткой выпуклого много­гранника, она должна удовлетворять ряду требований, связанных с особенностями многогранника. Например, фигуры на рис. 24.12 не являются развертками правильной четырехугольной пирамиды: в фигуре, изображенной на рис. 24.12, а, в вершине М сходятся четыре грани, чего не может быть в правильной четырехугольной пирамиде; а в фигуре, изображенной на рис. 24.12, б, боковые ребра А В и ВС не равны.

Вообще, развертку многогранника можно получить путем раз­резания его поверхности не только по ребрам. Пример такой раз­вертки куба приведен на рис. 24.13. Поэтому более точно развертку многогранника можно определить как плоский многоугольник, из которого может быть сделана поверхность этого многогранника без перекрытий.

Тела вращения

Телом вращения называют тело, полученное в результате вра­щения некоторой фигуры (обычно плоской) вокруг прямой. Эту прямую называют осью вращения.

Цилиндр - эго тело, которое получается в результате вращения прямоугольника вокруг одной из его сторон. При этом указанная сто­рона является осью цилиндра. На рис. 24.14 изображен цилиндр с осью ОО’, полученный в результате вращения прямоугольника АА"О"О вокруг прямой ОО". Точки О и О" - центры оснований цилиндра.

Цилиндр, который получается в результате вращения прямо­угольника вокруг одной из его сторон, называют прямым круго­вым цилиндром, так как его основаниями являются два равных круга, расположенных в параллельных плоскостях так, что отре­зок, соединяющий центры кругов, перпендикулярен этим плос­костям. Боковую поверхность цилиндра образуют отрезки, равные стороне прямоугольника, параллельной оси цилиндра.

Разверткой боковой поверхности пря­мого кругового цилиндра, если ее раз­резать по образующей, является прямо­угольник, одна сторона которого равна длине образующей, а другая - длине ок­ружности основания.

Конус - это тело, которое получает­ся в результате вращения прямоугольного треугольника вокруг одного из катетов.

При этом указанный катет неподвижен и называется осью конуса. На рис. 24.15 изображен конус с осью SO, получен­ный в результате вращения прямоуголь­ного треугольника SOA с прямым уг­лом О вокруг катета S0. Точку S называют вершиной конуса, ОА - радиусом его основания.

Конус, который получается в результате вращения прямоуголь­ного треугольника вокруг одного из его катетов, называют пря­мым круговым конусом, гак как его основанием является круг, а вершина проектируется в центр этого круга. Боковую поверхность конуса образуют отрезки, равные гипотенузе треугольника, при вращении которого образуется конус.

Если боковую поверхность конуса разрезать по образующей, то ее можно «развернуть» на плоскость. Разверткой боковой поверх­ности прямого кругового конуса является круговой сектор с ради­усом, равным длине образующей.

При пересечении цилиндра, конуса или любого другого тела вращения плоскостью, содержагцей ось вращения, получается осевое сечение. Осевое сечение цилиндра - прямоугольник, осевое сече­ние конуса - равнобедренный треугольник.

Шар - это тело, которое получается в результате вращения полукруг а вокруг его диаметра. На рис. 24.16 изображен шар, получен­ный в результате вращения полукруга вокруг диаметра АА". Точку О называют центром шара, а радиус круга является радиусом шара.

Поверхность шара называют сферой. Сферу развернуть на плос­кость нельзя.

Любое сечение шара плоскостью есть круг. Радиус сечения шара будет наибольшим, если плоскость проходит через центр шара. Поэтому сечение шара плоскостью, проходящей через центр шара, называют большим кругом шара, а окружность, его ограничиваю­щая, - большой окружностью.

ИЗОБРАЖЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ НА ПЛОСКОСТИ

В отличие от плоских фигур геометрические тела невозможно точно изобразить, например, на листе бумаги. Однако с помощью чертежей на плоскости можно получить достаточно наглядное изоб­ражение пространственных фигур. Для этого используются специ­альные способы изображения таких фигур на плоскости. Одним из них является параллельное проектирование.

Пусть даны плоскость а и пересекающая се прямая а. Возьмем в пространстве произвольную точку Л", не принадлежащую пря­мой а, и проведем через X прямую а", параллельную прямой а (рис. 24.17). Прямая а" пересекает плоскость в некоторой точке X", которая называется параллельной проекцией точки X на плос­кость а.

Если точка А"лежит на прямой а, то се параллельной проекци­ей X" является точка, в которой прямая а пересекает плоскость а.

Если точка X принадлежит плоскости а, то точка X" совпадает с точкой X.

Таким образом, если заданы плоскость а и пересекающая ее прямая а. то каждой точке X пространства можно поставить в соот­ветствие единственную точку А" - параллельную проекцию точки X на плоскость а (при проектировании параллельно прямой а). Плос­кость а называется плоскостью проекций. О прямой а говорят, что она залает направление проектирования - ггри замене прямой а любой другой параллельной ей прямой результат проектирования не изменится. Все прямые, параллельные прямой а, задаюз одно и то же направ­ление проектирования и называются вместе с прямой а проектирующими прямыми.

Проекцией фигуры F называют мно­жество F‘ проекцией всех се точек. Ото­бражение, сопоставляющее каждой точ­ке X фигуры F "ее параллельную проек­цию - точку X" фигуры F", называется параллельным проектированием фигуры F (рис. 24.18).

Параллельной проекцией реального предмета является его тень, падающая на плоскую поверхность при солнечном освещении, поскольку солнечные лучи можно считать параллельными.

Параллельное проектирование обладает рядом свойств, знание которых необходимо при изображении геометрических тел на плоскости. Сформулируем основные, не приводя их доказательства.

Теорема 24.1. При параллельном проектировании для прямых, не параллельных направлению проектирования, и для лежащих на них отрезков выполняются следующие свойства:

1) проекция прямой есть прямая, а проекция отрезка - отрезок;

2) проекции параллельных прямых параллельны или совпадают;

3) отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.

Из этой теоремы вытекает следствие: при параллельном про­ектировании середина отрезка проектируется в середину его про­екции.

При изображении геометрических тел на плоскости необходи­мо следить за выполнением указанных свойств. В остальном оно может быть произвольным. Так, углы и отношения длин непарал­лельных отрезков могут изменяться произвольно, т.е., например, треугольник при параллельном проектировании изображается про­извольным треугольником. Но если треугольник равносторонний, то па проекции его медианы должны соединять вершину треуголь­ника с серединой противоположной стороны.

И еще одно требование необходимо соблюдать при изображе­нии пространственных тел на плоскости - способствовать созда­нию верного представления о них.

Изобразим, например, наклонную призму, основаниями кото­рой являются квадраты.

Построим сначала нижнее основание призмы (можно начинать и с верхнего). По правилам параллельного проектирования огго изобразится произвольным параллелограммом АВСD (рис. 24.19, а). Так как ребра призмы параллельны, строим параллельные пря­мые, проходящие через вершины построенного параллелограмма и откладываем на них равные отрезки АА", ВВ’, СС", DD", длина которых произвольна. Соединив последовательно точки А", В", С", D", получим четырехугольник А"В"С"D", изображающий верхнее основание призмы. Нетрудно доказать, что А"В"С"D" - паралле­лограмм, равный параллелограмму АВСD и, следовательно, мы имеем изображение призмы, основаниями которой являются рав­ные квадраты, а остальные грани - параллелограммы.

Если нужно изобразить прямую призму, основаниями которой являются квадраты, то показать, что боковые ребра этой призмы перпендикулярны основанию, можно так, как это сделано на рис. 24.19, б.

Кроме тог о, чертеж на рис. 24.19, б можно считать изображени­ем правильной призмы, так как ее основанием является квадрат - правильный четырехугольник, а также - прямоугольным парал­лелепипедом, поскольку все его грани - прямоугольники.

Выясним теперь, как изобразить на плоскости пирамиду.

Чтобы изобразить правильную пирамиду, сначала чертят пра­вильный многоугольник, лежащий в основании, и его центр - точку О. Затем проводят вертикальный отрезок OS, изображаю­щий высоту пирамиды. Заметим, что вертикальность отрезка OS обеспечивает большую наглядность рисунка. И наконец, точку S соединяют со всеми вершинами основания.

Изобразим, например, правильную пирамиду, основанием ко­торой является правильный шестиугольник.

Чтобы верно изобразить при параллельном проектировании правильный шестиугольник, надо обратить внимание на следующее. Пусть АВСDЕF - правильный шестиугольник. Тогда ВСЕF - прямоугольник (рис. 24.20) и, значит, при параллельном проектировании он изобра­зится произвольным параллелограммом В"С"Е"F". Так как диагональ АD проходит через точку О - центр многоугольника АВСDЕF и параллельна отрезкам. ВС и ЕF и АО= ОD, то при параллельном проектировании она изобразится произвольным от­резком А"D", проходящим через точку О" параллельно В"С" и Е"F" и, кроме того, А"О" = О"D".

Таким образом, последовательность построения основания ше­стиугольной пирамиды такова (рис. 24.21):

§ изображают произвольный параллелограмм В"С"Е"F" и его диагонали; отмечают точку их пересечения O";

§ через точку О" проводят прямую, параллельную В’С" (или Е"F’);

§ на построенной прямой выбирают произвольную точку А" и отмечают точку D" такую, что О"D" = А"О", и соединяют точку А" с точками В" и F ", а точку D" - с точками С" и Е".

Чтобы завершить построение пирамиды, проводят вертикаль­ный отрезок ОS (его длина выбирается произвольно) и соединя­ют точку S со всеми вершинами основания.

При параллельном проектировании шар изображается в виде круга того же радиуса. Чтобы сделать изображение шара более на­глядным, рисуют проекцию какой-нибудь большой окружности, плоскость которой не перпендикулярна плоскости проекции. Эта проекция будет эллипсом. Центр шара изобразится центром этого эллипса (рис. 24.22). Теперь можно найти соответствующие полюсы N и S при условии, что отрезок, их соединяющий, перпендикуля­рен плоскости экватора. Для этого через точку О проводим пря­мую, перпендикулярную АВ и отмечаем точку С - пересечение этой прямой с эллипсом; затем через точку С проводим касатель­ную к эллипсу, изображающему экватор. Доказано, что расстоя­ние СМ равно расстоянию от центра шара до каждого из полюсов. Поэтому, отложив отрезки ОN и OS, равные СМ, получим полю­сы N и S.

Рассмотрим один из приемов построения эллипса (он основан на преобразовании плоскости, которое называется сжатием): строят окружность с диаметром и проводят хорды, перпендикулярные диаметру (рис. 24.23). Половину каждой из хорд делят пополам и полученные точки соединяют плавной кривой. Эта кривая - эл­липс, большой осью которого является отрезок АВ, а центром - точка О.

Этот прием мЬжно использовать, изображая на плоскости пря­мой круговой цилиндр (рис. 24.24) и прямой круговой конус (рис. 24.25).

Прямой круговой конус изображают так. Сначала строят эл­липс - основание, затем находят центр основания - точку О и перпендикулярно проводят отрезок OS, который изображает вы­соту конуса. Из точки S проводят к эллипсу касательные (это дела­ют «на глаз», прикладывая линейку) и выделяют отрезки SС и SD этих прямых от точки S до точек касания С и D. Заметим, что отрезок СD не совпадает с диаметром основания конуса.

Многогранники

Многогранник - это такое тело, поверхность которого состоит из конечной количества плоских многоугольников. Многогранник называется выпуклым , если он лежит по одну сторону от плоскости каждого из плоских многоугольников на его поверхности. Общая часть такой плоскости и поверхности выпуклого многоугольника называется гранью .
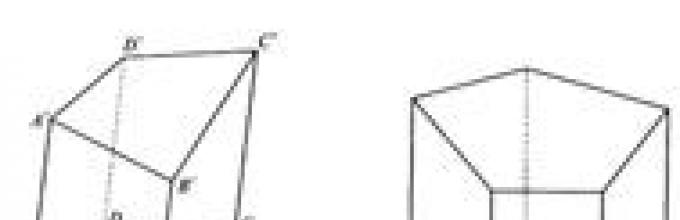
На рисунке ниже слева изображен неопуклий многогранник; на рисунке справа - выпуклый.

Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника , а вершины граней - вершинами многогранника .

Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников (см. рисунок). Многоугольники называются основами призмы , а отрезки, соединяющие соответствующие вершины, - боковыми ребрами призмы .

Обозначения: .
Боковая поверхность призмы состоит из параллелограммов. Каждый из них имеет две стороны, которые являются соответствующими сторонами основания, а две другие - смежными боковыми ребрами. Основания призмы равны и лежат в параллельных плоскостях. Боковые ребра призмы параллельные и равны. Высотой призмы называется расстояние между плоскостями ее оснований.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы . (На рисунке - высота, и - диагонали.)
Диагональные сечения - это сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани (см. рисунки).

Призма называется прямой , если ее боковые ребра перпендикулярны к основаниям. В противном случае призма называется наклонной .
Боковые грани прямой призмы - прямоугольники, высота прямой призмы равна боковому ребру, диагональные сечения являются прямоугольниками.
Боковой поверхностью призмы называется сумма площадей боковых граней. Полная поверхность призмы равна сумме боковой поверхности и площадей оснований.
Теорема 1. Боковая поверхность прямой призмы равна произведению периметра основания и высоты, то есть длины бокового ребра.
Перпендикулярным сечением призмы будем называть сечение плоскостью, перпендикулярной к боковому ребру призмы (а это означает, что эта плоскость является перпендикулярной всех боковых ребер призмы).
Теорема 2. Боковая поверхность наклонной призмы равен произведению длины бокового ребра и периметра перпендикулярного сечения.
На рисунке - перпендикулярное сечение.
S б = H ⋅ P осн;
S п = S б + 2S осн.
S б = l ⋅ P тэр;
S п = S б + 2S осн.

Очевидно, что эта теорема верна и в случае прямой призмы, ибо тогда перпендикулярное сечение будет сечением плоскостью, параллельной плоскостям оснований призмы.
Обратите внимание: если некоторый многоугольник является перпендикулярным сечением призмы, то его внутренние углы являются линейными углами двугранных углов между соответствующими боковыми гранями.
В случае прямой призмы линейными углами двугранных углов между боковыми гранями являются непосредственно углы основы.
Пример
На рисунке - прямая призма.

- линейный угол двугранного угла между гранями и .
Призма называется правильной , если:
в основе ее лежит правильный многоугольник;
призма является прямой.
Параллелепипед
Собой параллелепипед называется призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда - параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противоположными .
Теорема 1. Противоположные грани параллелепипеда являются параллельными и равными.
Параллелепипед остается собой параллелепипед во всех случаях, когда за его основу считаем любую его грань (см. рисунок).
Теорема 2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Из этого следует, что точка пересечения диагоналей параллелепипеда есть его центром симметрии.
Обратите внимание: у прямого параллелепипеда четыре диагонали, попарно равны друг другу.
На рисунке ; .
Это следует из свойств наклонных, поскольку - уровне перпендикуляры к плоскости основания ABCD.

Если две диагонали прямого параллелепипеда выходящие из соседних вершин, то большая из них та, которая проектируется в большую диагональ основания, то есть такую диагональ параллелограмма, которая лежит против тупого угла. Итак, если на приведенном выше рисунке считать угол ABC тупой, получим , .
Прямой параллелепипед, в которого основой является прямоугольник, называется прямоугольным собой параллелепипед (см. рисунок).

Все грани прямоугольного параллелепипеда - прямоугольники, которые можно разбить на три пары равных между собой. Произвольную грань прямоугольного параллелепипеда можно считать его основой. Учитывая, что при параллельном проектировании произвольный параллелограмм может изображаться произвольным параллелограммом, изображение прямоугольного параллелепипеда никак не отличается от изображения любого прямого параллелепипеда.
Длины непараллельных ребер называются линейными размерами (измерениями) прямоугольного параллелепипеда.
Теорема 3. В прямоугольном параллелепипеде все диагонали равны. Квадрат диагонали равен сумме квадратов трех его измерений.
Все двугранные углы прямоугольного параллелепипеда являются прямыми.
Прямоугольный параллелепипед имеет три пары равных между собой диагональных сечений. Каждый из этих сечений является прямоугольником (см. рисунки).

Каждая пара сечений пересекаются по прямой, которая проходит через точки пересечения диагоналей противоположных граней. Отрезки между этими точками являются параллельными и равны одному из ребер прямоугольного параллелепипеда.
Прямоугольным является треугольник, который образуется диагональю прямоугольного параллелепипеда, диагональю боковой грани и стороной основания (см. рисунок). Например, .

Прямоугольный параллелепипед имеет центр симметрии - это точка пересечения его диагоналей.
Он также имеет три плоскости симметрии, проходящие через центр симметрии параллельно граням.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом .
Плоскость любого диагонального сечения куба является его плоскостью симметрии. Таким образом, куб имеет девять плоскостей симметрии.
На рисунке рассмотрим взаимное расположение некоторых элементов прямого параллелепипеда:

- угол между диагональю боковой грани и плоскостью основания ( - перпендикуляр, - наклонная, СD - проекция).
- угол между диагональю прямого параллелепипеда и плоскостью основания ( - перпендикуляр, - наклонная, АС - проекция).
- угол наклона диагонали боковой грани (AD - перпендикуляр, - наклонная, - проекция).
Пусть - прямой параллелепипед (см. рисунок), где ABCD - ромб. Проведем его сечение плоскостью, проходящей через диагональ основания BD и вершину .

В сечении получим равнобедренный треугольник .
- линейный угол двугранного угла между плоскостями основания и сечения. по свойству диагоналей ромба, - перпендикуляр, - наклонная, СО - проекция. По теореме о трех перпендикуляры: .
Пирамида
Пирамидой называется многогранник, который состоит из плоского многоугольника - основания пирамиды, точки, не лежащей в плоскости основания - вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами .
Высота пирамиды - перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида называетсяn -угольной , если ее основанием является n -угольник. Треугольная пирамида называется также тетраэдром . Боковая грань пирамиды - треугольник. Одной из его вершин является вершина пирамиды, а противоположной стороной - сторона основания пирамиды.
На рисунке SO - высота пирамиды. Тогда - угол между боковым ребром и плоскостью основания (SO - перпендикуляр, ЅА - наклонная, ОА - проекция).

Из основания высоты пирамиды (точки А ) проведем перпендикуляр на сторону основания (например, АЕ ). Основание этого перпендикуляра (точку F ) соединим с вершиной пирамиды (точка S ). По теореме о трех перпендикуляры: . (SO - перпендикуляр, SP - наклонная, OF - проекция, по построению.) Следовательно, - линейный угол двугранного угла между плоскостью боковой грани ASE и плоскостью основания.
Для решения задач о пирамиде очень важно выяснять, где размещена основа ее высоты.
1. Если выполняется хотя бы одно из следующих условий:
все боковые ребра пирамиды равны;
все боковые ребра наклонены к плоскости основания под одним и тем же углом;
все боковые ребра образуют одинаковые углы с высотой пирамиды;
все боковые ребра равноудалены от основания высоты, то основанием высоты пирамиды является центр окружности, описанной вокруг основания пирамиды.
Боковое ребро l , высота H и радиус R описанной вокруг основания окружности образуют прямоугольный треугольник:

В этом случае боковую поверхность можно найти по формуле , где l - длина бокового ребра, , ... - плоские углы при вершине.
2. Если выполняется хотя бы одно из следующих условий:
все боковые грани наклонены к плоскости основания под одним и тем же углом;
все боковые грани имеют одинаковые высоты;
высоты боковых граней образуют одинаковые углы с высотой пирамиды;
боковые грани равноудалены от основания высоты, - то основание высоты лежит в центре круга, вписанного в основание пирамиды.
На рисунке - прямоугольный , - радиус вписанной окружности в ABCDEF ;

- высота пирамиды, SP - высота боковой грани;
- линейный угол двугранного угла между боковой гранью и плоскостью основания;
О - центр вписанной в основание окружности, то есть точка пересечения биссектрис ABCDEF .
В этом случае .
3. Если боковое ребро перпендикулярно к плоскости основания, то это ребро является высотой пирамиды (см. рисунки).

В этом случае и - углы наклона боковых ребер ЅВ и ЅС соответственно к плоскости основания. является линейным углом двугранного угла между боковыми гранями SAC и SBA .
4. Если боковая грань перпендикулярна к плоскости основания (см. рисунок), то высотой пирамиды будет высота этой грани (по теореме «Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна к прямой их пересечения, то она перпендикулярна ко второй плоскости»).
5. Если две боковые грани перпендикулярны к плоскости основания, то высотой пирамиды является их общее боковое ребро.
Расстояния от основания высоты пирамиды
Расстояние от основания высоты пирамиды до бокового ребра - перпендикуляр, опущенный из точки О на это ребро (см. рисунок). Обратите внимание: , но на рисунке не должен быть прямым: углы при параллельном проектировании не сохраняются.
OF - расстояние от основания высоты до бокового ребра SE ;
ON - расстояние от основания высоты до боковой грани ASB (о это расстояние подробнее смотри ниже).

, где - угол между ребром SE и плоскостью основания.
Расстояние от основания высоты до боковой грани
Пусть , тогда по теореме о трех перпендикуляры. Следовательно, AB перпендикулярна к плоскости SOK . Отсюда, если , то ON перпендикулярна к плоскости ASB .
.
Пирамида называется правильной , если ее основанием является правильный многоугольник, а основание высоты совпадает с центром многоугольника. Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны, боковые грани - равные равнобедренные треугольники. Высота боковой грани, проведенная из вершины пирамиды, называется апофемою . Она является биссектрисой и медианой боковой грани, так и является равнобедренным треугольником.
Теорема. Боковая поверхность правильной пирамиды равна произведению півпериметра основания на апофему.
; ,
где Р - периметр основания, а - сторона основания, l - длина апофеми.
Правильная треугольная пирамида
В основании правильной треугольной пирамиды лежит равносторонний треугольник изображается произвольным треугольником (см. рисунок).

Центром является точка пересечения его биссектрис, которые одновременно являются высотами и медіанами. Медианы при параллельном проектировании изображаются медіанами. Поэтому строим две медианы основания. Точка их пересечения - основание высоты пирамиды. Изображаем высоту, а затем соединяем вершину пирамиды с вершинами основания. Получим боковые ребра.
На рисунке: - угол наклона бокового ребра к плоскости основания (одинаковый для всех ребер); - угол наклона боковой грани к плоскости основания (одинаковая для всех граней).
Пусть .
Тогда ; ; ;
; ; .
Следовательно, .
; .
Плоскость осевого сечения ASD является плоскостью симметрии правильной треугольной пирамиды.
Эта плоскость перпендикулярна к плоскости основания и плоскости грани BSC .
Интересно также отметить, что скрещивающиеся ребра пирамиды (SA и BC , SB и AC , SC и AB ) являются перпендикулярными. Если , то ON является расстоянием от основания высоты не только к анафеме, но и к боковой грани BSC .
.
Правильная четырехугольная пирамида
В основании правильной четырехугольной пирамиды лежит квадрат, который изображается произвольным параллелограммом. Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
Пусть сторона квадрата а (см. рисунок).
Тогда ;
;
;
;
.

Обратите внимание: , , то есть .
При параллельном проектировании параллельность сохраняется.
; .
Расстояние от основания высоты до боковой грани:
; .

Правильная шестиугольная пирамида
В основе правильной шестиугольной пирамиды лежит правильный шестиугольник (см. рисунок). Его центром является точка пересечения диагоналей. Эта точка - основание высоты пирамиды.
Тогда ;
Пусть сторона правильного шестиугольника а .
;
;

.
; .

Усеченная пирамида
Срезанной пирамидой называется многогранник, который останется, если от пирамиды отделить плоскостью, которая параллельна основе, пирамиду с той же вершиной.
Теорема. Плоскость, параллельная основании пирамиды и пересекающая ее, отсекает подобную пирамиду.
Обратите внимание: чтобы правильно изобразить срезанную пирамиду, надо начинать с изображения исходной полной пирамиды (см. рисунок).

Основания усеченной пирамиды - подобные многоугольники. Боковые грани - трапеции. - высота усеченной пирамиды, высота боковой грани - угол наклона бокового ребра к плоскости основания (любой), - угол наклона боковой грани к плоскости нижнего основания.
Правильная усеченная пирамида - это усеченная пирамида, которую достали из правильной пирамиды.
Ее боковые ребра равны и наклонены к плоскости основания под одним и тем же углом. Ее боковые грани равны рівнобічній трапеции и наклонены к плоскости нижнего основания под одним и тем же углом. Высоты боковых граней пирамиды называются апофемами .
Боковая поверхность правильной усеченной пирамиды равна произведению половину суммы периметров оснований и апофеми.
, где P н и P в - периметры соответствующих оснований, l - апофема.
На рисунках изображены фигуры, которые бывает очень полезным рассмотреть при решении задач на срезанную пирамиду.
;
.

;


- прямоугольная трапеция.
- высота усеченной пирамиды.
- высота боковой грани.

В случае, когда усеченная пирамида правильная, отрезки OD и являются радиусами описанной окружности, а OF и - радиусами вписанной окружности для нижней и верхней основы соответственно.

Правильные многогранники
Выпуклый многогранник называется правильным , если его грани являются правильными многогранниками с одним и тем же количеством сторон, а в каждой вершине многогранника совпадает одно и то же число ребер.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
1. У правильного тетраэдра грани - правильные треугольники; в каждой вершине совпадает по три ребра. Тетраэдр - треугольная пирамида, все ребра которой равны.
2. У куба все грани - квадраты; в каждой вершине совпадает по три ребра. Куб - прямоугольный параллелепипед с равными ребрами.
3. У октаэдра грани - правильные треугольники. В каждой его вершине совпадает по четыре ребра.
4. В додекаедра грани - правильные п"ятикутники. В каждой его вершине совпадает по три ребра.
5. У икосаэдра грани - правильные треугольники. В каждой его вершине совпадает по пять ребер.
На рисунках приведены примеры правильных многогранников с названиями.

Получил широкую известность благодаря участию в сериале "Большая любовь". Однако актера также можно увидеть в еще нескольких известных проектах, таких как сериал "Секретные материалы", "Место преступления: Майами".

Интересно, что такой миловидный актер не употребляет никаких продуктов животного происхождения. Он - абсолютный вегетарианец.

Ранние годы и путь к актерству

Маленький Дуглас родился в Канаде, в провинции Онтарио. Мальчик появился в семье учительницы и продюсера низкобюджетных фильмов. Симпатяга Дуглас обрадовал родителей своим появлением 22 июня 1985 года. У парня есть два брата и сестра: Грегори, Андре и Саманта Смит. Грегори, как и Дуглас, является актером.

Братья родились в семье продюсера, и наверняка это определило их судьбу. С 11 лет маленький, но целеустремленный актер Дуглас Смит вплотную занялся актерским мастерством. Кстати, у парня есть опыт игры на сцене, например в комедии Шекспира "Двенадцатая ночь" в роли Мальволио.

Первым фильмом, в котором принял участие Дуглас, стал "Смертельный вызов" (1996), где он исполнил крохотную роль.

Фильмы

Дуглас Смит получил свою первую роль в большом кино в киноленте "Взрыв из прошлого" (1999), где ему удалось поработать с такими известными актерами, как и Брендан Фрейзер. Далее молодой и амбициозный актер не уставал много работать и хватался за разные проекты. Так он снимался и в кино, и в телесериалах, которые принесли ему особую популярность.

Сериалы, с участием актера Дугласа Смита:

В кинопортфолио Смита входит также ряд фильмов. Где-то он играет маленькие эпизодические роли, а некоторые фильмы достаточно популярны и на слуху у многих киноманов:


Личная жизнь

Если человек талантлив, то он имеет как минимум еще один талант. Актер Дуглас Смит участвует в группе Alaskan Summer, где, кстати, также трудится и девушка актера - Эштон Лансфорд. Похоже, у ребят все серьезно, ведь не каждый выдержит партнера круглые сутки - дома и на работе.

Кстати, парень сам пишет песни и исполняет их в своей группе.

Многогранники представляют собой простейшие тела в пространстве, подобно тому как многоугольники – простейшие фигуры на плоскости. Многогранные формы мы видим ежедневно: спичечный коробок, книга, комната, многоэтажный дом (с горизонтальной крышей) – прямоугольные параллелепипеды; молочные пакеты-тетраэдры или тоже параллелепипеды; граненый карандаш, гайка дают представление о призмах (впрочем, параллелепипед – это тоже четырехугольная призма). Многие архитектурные сооружения или их детали представляют собой пирамиды или усеченные пирамиды – такие формы имеют знаменитые египетские пирамиды или башни Кремля. Многие многогранные формы, например «домик» на рис. 1 и «круглый дом» на рис. 2, не имеют специальных названий. С чисто геометрической точки зрения многогранник – это часть пространства, ограниченная плоскими многоугольниками – гранями. Стороны и вершины граней называют ребрами и вершинами самого многогранника. Грани образуют так называемую многогранную поверхность. Чтобы исключить из рассмотрения многогранные фигуры типа изображенных на рис. 3, которые не принято называть многогранниками, на многогранную поверхность обычно накладывают такие ограничения:

1) каждое ребро должно являться общей стороной двух, и только двух, граней, называемых смежными;

2) каждые две грани можно соединить цепочкой последовательно смежных граней;

3) для каждой вершины углы прилежащих к этой вершине граней должны ограничивать некоторый многогранный угол.

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой из его граней. Это условие эквивалентно каждому из двух других: 1) отрезок с концами в любых двух точках многогранника целиком лежит в многограннике, 2) многогранник можно представить как пересечение нескольких полупространств.

Для любого выпуклого многогранника справедлива формула Эйлера (см. Топология), устанавливающая связь между числом вершин В, ребер Р и граней Г:

Для невыпуклых многогранников это соотношение, вообще говоря, неверно, например для многогранной поверхности, изображенной на рис. 2; , , поэтому . Число называется эйлеровой характеристикой многогранника и может равняться . Эйлерова характеристика показывает, грубо говоря, сколько «дырок» имеет многогранник. Число дырок (или ).

Простейшая классификация по числу вершин (углов, сторон) для многогранников неэффективна. Самые простые многогранники – четырехвершинники или четырехгранники – всегда ограничены четырьмя треугольными гранями. Но уже пятигранники могут быть совершенно разных типов, например: четырехугольная пирамида ограничена четырьмя треугольниками и одним четырехугольником (рис. 4,а), а треугольная призма ограничена двумя треугольниками и тремя четырехугольниками (рис. 4,б). Примеры пятивершинников – четырехугольная пирамида и треугольный диэдр (рис. 4,в).

Самые распространенные в окружающем нас мире многогранники, конечно, имеют специальные названия. Так, -угольная пирамида имеет -угольник в основании и боковых треугольных граней, сходящихся в общей вершине треугольников (рис. 4,а, где ); -угольная призма ограничена двумя равными, параллельными и одинаково расположенными -угольниками – основаниями – и параллелограммами – боковыми гранями, соединяющими соответственные стороны оснований (рис. 4,б, где ).

Промежуточное положение между пирамидами и призмами занимают усеченные пирамиды, получающиеся из пирамид отсечением меньших пирамид параллельными основаниям плоскостями (рис. 5). Среди природных форм кристаллов встречаются диэдры, или бипирамиды, составленные из двух пирамид с общим основанием (рис. 4,в). Архимед рассматривал также -угольные антипризмы, ограниченные двумя параллельными, но повернутыми друг относительно друга -угольниками и соединяющими их, как показано на рис. 6, -треугольниками (при большом антипризма похожа на пионерский барабан - рис. 6).

Как и многоугольники, многогранники классифицируют также по степени их симметричности. Среди пирамид выделяют правильные: в основании у них лежит правильный многоугольник, а высота – перпендикуляр, проведенный из вершины к плоскости основания,- попадает в центр основания пирамиды.

Аналогом параллелограмма является параллелепипед; так же как параллелограмм, параллелепипед имеет центр симметрии, в котором пересекаются и делятся пополам все четыре диагонали (отрезки, соединяющие вершины, не принадлежащие одной грани). Правильные призмы в основаниях имеют правильные многоугольники, расположенные так, что прямая, проходящая через их центры, перпендикулярна плоскостям оснований. Так же должны быть расположены и основания правильной -угольной антипризмы, но только одно основание должно быть повернуто на угол относительно другого. Все правильные многогранники имеют довольно много самосовмещений – поворотов и симметрий, переводящих многогранник в себя. Совокупность всех самосовмещений, считая и тождественное, образует так называемую группу симметрий многогранника. По группам симметрий в кристаллографии классифицируют монокристаллы, имеющие, как правило, многогранную форму.

Симметричность, правильность рассмотренных выше многогранников не совсем полные – у них могут существовать неравные грани, разные многогранные углы. Исключение составляют три многогранника: правильный тетраэдр – правильная треугольная пирамида с равными ребрами, ограниченная четырьмя правильными треугольниками (рис. 7,а); куб, или правильный гексаэдр, - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами (рис. 7,б); наконец, октаэдр – правильный четырехугольный диэдр с равными ребрами, ограниченный восемью правильными треугольниками (рис. 7,в); октаэдр можно определить и как правильную треугольную антипризму с равными ребрами. В отличие от произвольных правильных пирамид, призм, диэдров и антипризм – тетраэдр, куб, октаэдр таковы, что любые их две грани (и любые два многогранных угла) можно совместить с помощью некоторого самосовмещения всего многогранника. Кроме того, их многогранные углы правильные, т.е. имеют равные плоские и равные двугранные углы.

Аналогично правильным многоугольникам на плоскости можно определить и правильные многогранники «вообще»: это выпуклые многогранники, ограниченные равными правильными многоугольниками и имеющие равные правильные многогранные углы. Оказывается, кроме трех названных выше видов правильных многогранников – правильного тетраэдра, куба и октаэдра – существуют еще только два вида правильных многогранников: додекаэдр (двенадцатигранник) и икосаэдр (двадцатигранник), ограниченные соответственно 12 правильными пятиугольниками и 20 правильными треугольниками, - рис. 8,а,б. Эти два многогранника связаны между собой так же, как куб и тетраэдр (см. Куб): центры граней додекаэдра являются вершинами икосаэдра – рис. 9, - и наоборот.

Сам факт существования всего пяти действительно правильных многогранников удивителен – ведь правильных многоугольников на плоскости бесконечно много.

Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, XIII книга знаменитых «Начал» Евклида. Эти многогранники часто называют также Платоновыми телами – в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном, четыре из них олицетворяли четыре стихии: тетраэдр – огонь, куб – землю, икосаэдр – воду и октаэдр – воздух; пятый же многогранник, додекаэдр, символизировал все мироздание – его по-латыни стали называть quinta essentia («пятая сущность»). Придумать правильный тетраэдр, куб, октаэдр, по-видимому, было нетрудно, тем более что эти формы имеют природные кристаллы, например: куб – монокристалл поваренной соли (NaCl), октаэдр – монокристалл алюмокалиевых квасцов . Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS). Имея же додекаэдр, нетрудно построить и икосаэдр: как уже говорилось, его вершинами будут центры двенадцати граней додекаэдра – рис. 9.