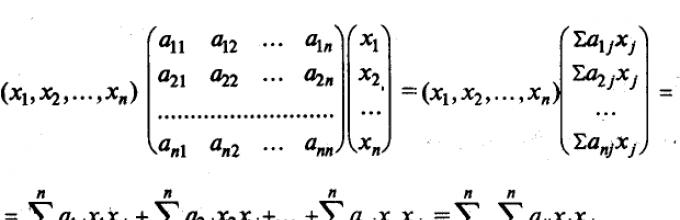Квадратичной формой f(х 1 , х 2 ,...,х n) от n переменных называют сумму, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятым с некоторым коэффициентом:f(х 1 , х 2 ,...,х n) = (a ij =a ji).

Матрицу А, составленную из этих коэффициентов, называют матрицей квадратичной формы. Это всегда симметрическая матрица (т.е. матрица, симметричная относительно главной диагонали,a ij =a ji).

В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где

В самом деле

Например, запишем в матричном виде квадратичную форму .

Для этого найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, а остальные элементы - половинам соответствующих коэффициентов квадратичной формы. Поэтому

Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) =Y T (C T AC)Y.

Таким образом, при невырожденном линейном преобразовании С матрица квадратичной формы принимает вид: А * =C T AC.

Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формыf(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .

Квадратичная форма называется канонической (имеетканонический вид ), если все ее коэффициентыa ij = 0 приi≠j, т.е.f(х 1 , х 2 ,...,х n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .

Ее матрица является диагональной.

Теорема (доказательство здесь не приводится). Любая квадратичная форма может быть приведена к каноническому виду с помощью невырожденного линейного преобразования.

Например, приведем к каноническому виду квадратичную форму f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 .

Для этого вначале выделим полный квадрат при переменной х 1:

f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 – х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 – х 2 х 3 .

Теперь выделяем полный квадрат при переменной х 2:

f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 – 5(х 2 2 – 2* х 2 *(1/10)х 3 + (1/100)х 3 2) - (5/100)х 3 2 = = 2(x 1 + х 2) 2 – 5(х 2 – (1/10)х 3) 2 - (1/20)х 3 2 .

Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 ,y 2 = х 2 – (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому видуf(y 1 ,y 2 ,y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами 1). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называютзаконом инерции квадратичных форм .

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2:f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 = -3х 2 2 – х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 – - 2* х 2 ((1/6) х 3 + (2/3)х 1) +((1/6) х 3 + (2/3)х 1) 2) – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 = = -3(х 2 – (1/6) х 3 - (2/3)х 1) 2 – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 =f(y 1 ,y 2 ,y 3) = -3y 1 2 - -3y 2 2 + 2y 3 2 , гдеy 1 = - (2/3)х 1 + х 2 – (1/6) х 3 ,y 2 = (2/3)х 1 + (1/6) х 3 и y 3 = x 1 . Здесь положительный коэффициент 2 приy 3 и два отрицательных коэффициента (-3) приy 1 иy 2 (а при использовании другого способа мы получили положительный коэффициент 2 приy 1 и два отрицательных – (-5) приy 2 и (-1/20) приy 3).

Также следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы , равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.

Квадратичную форму f(X) называютположительно (отрицательно )определенной , если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е.f(X) > 0 (отрицательна, т.е.f(X) < 0).

Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная формаf 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в видеf 2 (X) = -(x 1 - х 2) 2 .

В большинстве практических ситуации установить знакоопределенность квадратичной формы несколько сложнее, поэтому для этого используют одну из следующих теорем (сформулируем их без доказательств).

Теорема . Квадратичная форма является положительно (отрицательно) определенной тогда и только тогда, когда все собственные значения ее матрицы положительны (отрицательны).

Теорема (критерий Сильвестра) . Квадратичная форма является положительно определенной тогда и только тогда, когда все главные миноры матрицы этой формы положительны.

Главным (угловым) минором k-го порядка матрицы Аn-го порядка называют определитель матрицы, составленный из первыхkстрок и столбцов матрицы А ().

Отметим, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, причем минор первого порядка должен быть отрицательным.

Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 .

= (2 -)* *(3 -) – 4 = (6 - 2- 3+ 2) – 4 = 2 - 5+ 2 = 0;D= 25 – 8 = 17; . Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = 2 > 0. Главный минор второго порядка 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (-2 -)* *(-3 -) – 4 = (6 + 2+ 3+ 2) – 4 = 2 + 5+ 2 = 0;D= 25 – 8 = 17; . Следовательно, квадратичная форма – отрицательно определенная.

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = = -2 < 0. Главный минор второго порядка 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – отрицательно определенная (знаки главных миноров чередуются, начиная с минуса).

И в качестве еще одного примера исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (2 -)* *(-3 -) – 4 = (-6 - 2+ 3+ 2) – 4 = 2 +- 10 = 0;D= 1 + 40 = 41; . Одно из этих чисел отрицательно, а другое – положительно. Знаки собственных значений разные. Следовательно, квадратичная форма не может быть ни отрицательно, ни положительно определенной, т.е. эта квадратичная форма не является знакоопределенной (может принимать значения любого знака).

Способ 2. Главный минор первого порядка матрицы А  1 =a 11 = 2 > 0. Главный минор второго порядка 2 = = -6 – 4 = -10 < 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).

1Рассмотренный способ приведения квадратичной формы к каноническому виду удобно использовать, когда при квадратах переменных встречаются ненулевые коэффициенты. Если их нет, осуществить преобразование все равно возможно, но приходится использовать некоторые другие приемы. Например, пустьf(х 1 , х 2) = 2x 1 х 2 = x 1 2 + 2x 1 х 2 + х 2 2 - x 1 2 - х 2 2 =

= (x 1 + х 2) 2 - x 1 2 - х 2 2 = (x 1 + х 2) 2 – (x 1 2 - 2x 1 х 2 + х 2 2) - 2x 1 х 2 = (x 1 + х 2) 2 – - (x 1 - х 2) 2 - 2x 1 х 2 ; 4x 1 х 2 = (x 1 + х 2) 2 – (x 1 - х 2) 2 ;f(х 1 , х 2) = 2x 1 х 2 = (1/2)* *(x 1 + х 2) 2 – (1/2)*(x 1 - х 2) 2 =f(y 1 ,y 2) = (1/2)y 1 2 – (1/2)y 2 2 , гдеy 1 = х 1 + х 2 , аy 2 = х 1 – х 2 .

В этом параграфе мы остановимся на специальном, но важном классе положительных квадратичных форм.

Определение 3. Вещественная квадратичная форма называется неотрицательной (неположительной), если при любых вещественных значениях переменных

. (35)

В этом случае симметрическая матрица коэффициентов называется положительно полуопределенной (отрицательно полуопределенной).

Определение 4. Вещественная квадратичная форма называется положительно определенной (отрицательно определенной), если при любых не равных одновременно нулю вещественных значениях переменных

. (36)

В этом случае матрица также называется положительно определенной (отрицательно определенной).

Класс положительно определенных (отрицательно определенных) форм является частью класса неотрицательных (соответственно неположительных) форм.

Пусть дана неотрицательная форма . Представим ее в виде суммы независимых квадратов:

. (37)

В этом представлении все квадраты должны быть положительными:

. (38)

Действительно, если бы какое-либо было , то можно было бы подобрать такие значения , при которых

Но тогда при этих значениях переменных форма имела бы отрицательное значение, что по условию невозможно. Очевидно, что и обратно, из (37) и (38) следует положительность формы .

Таким образом, неотрицательная квадратичная форма характеризуется равенствами .

Пусть теперь – положительно определенная форма. Тогда и неотрицательная форма. Поэтому она представима в виде (37), где все положительны. Из положительной определенности формы следует, что . Действительно, в случае можно подобрать такие не равные одновременно нулю значения , при которых все обращались бы в нуль. Но тогда в силу (37) при , что противоречит условию (36).

Легко видеть, что и обратно, если в (37) и все положительны, то – положительно определенная форма.

Другими словами, неотрицательная форма тогда и только тогда является положительно определенной, когда она не сингулярна.

Следующая теорема дает критерий положительной определенности формы в виде неравенств, которым должны удовлетворять коэффициенты формы. При этом используются уже встречавшиеся в предыдущих параграфах обозначения для последовательных главных миноров матрицы :

Теорема 3. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы выполнялись неравенства

Доказательство. Достаточность условий (39) следует непосредственно из формулы Якоби (28). Необходимость условий (39) устанавливается следующим образом. Из положительной определенности формы следует положительная определенность «урезанных» форм

Но тогда все эти формы должны быть несингулярны, т. е.

Теперь мы имеем возможность воспользоваться формулой Якоби (28) (при ). Поскольку в правой части этой формулы все квадраты должны быть положительными, то

Отсюда следуют неравенства (39). Теорема доказана.

Поскольку любой главный минор матрицы при надлежащей перенумерации переменных можно поместить в левый верхний угол, то имеет место

Следствие. В положительно определенной квадратичной форме все главные миноры матрицы коэффициентов положительны:

Замечание. Из неотрицательности последовательных главных миноров

не следует неотрицательность формы . Действительно, форма

в которой , удовлетворяет условиям , но не является неотрицательной.

Однако имеет место следующая

Теорема 4. Для того чтобы квадратичная форма была неотрицательной, необходимо и достаточно, чтобы все главные миноры ее матрицы коэффициентов были неотрицательны:

Доказательство. Введем вспомогательную форму была неположительной, необходимо и достаточно, чтобы имели место неравенства

Назначение сервиса . Онлайн-калькулятор используется для нахождения матрицы Гессе и определения вида функции (выпуклая или вогнутая) (см. пример). Решение оформляется в формате Word . Для функции одной переменной f(x) определяются интервалы выпуклости и вогнутости .

Правила ввода функций :

Дважды непрерывно дифференцируемая функция f(x) является выпуклой (вогнутой) тогда и только тогда, когда матрица Гессе функции f(x) по x положительно (отрицательно) полуопределена для всех x (см. точки локальных экстремумов функции многих переменных).

Критические точки функции:

если гессиан положительно определён, то x 0 - точка локального минимума функции f(x) ,
если гессиан отрицательно определён, то x 0 - точка локального максимума функции f(x) ,
если гессиан не является знакоопределённым (принимает как положительные, так и отрицательные значения) и невырожден (det G(f) ≠ 0), то x 0 - седловая точка функции f(x).

Критерии определенности матрицы (теорема Сильвестра)

Положительная определенность :

все диагональные элементы матрицы должны быть положительны;
все ведущие главные определители должны быть положительны.

Для положительно полуопределённых матриц критерий Сильвестра звучит подобным образом: Форма положительно полуопределена тогда и только тогда, когда все главные миноры неотрицательны. Если матрица Гессе в точке положительно полуопределена (все главные миноры неотрицательные), то это точка минимума (однако, если гессиан полуопределен, а один из миноров равен 0, то это может быть и седловая точка. Нужны дополнительные проверки).

Положительная полуопределенность:

все диагональные элементы неотрицательны;
все главные определители неотрицательны.

Главный определитель – это определитель главного минора.

Квадратная симметрическая матрица порядка n , элементами которой являются частные производные целевой функции второго порядка, называется матрицей Гессе и обозначается:

Для того, чтобы симметрическая матрица была положительно определена, необходимо и достаточно, чтобы все ее диагональные миноры были положительны, т.е.

для матрицы A = (a ij) положительные.

Отрицательная определенность .
Для того чтобы симметрическая матрица была отрицательно определена, необходимо и достаточно, чтобы имели место неравенства:
(-1) k D k > 0, k =1,.., n.
Другими словами, для того, чтобы квадратичная форма была отрицательно определённой , необходимо и достаточно, чтобы знаки угловых миноров матрицы квадратичной формы чередовались, начиная со знака минус. Например, для двух переменных, D 1 < 0, D 2 > 0.

Если гессиан полуопределен, то это может быть и точка перегиба. Нужны дополнительные исследования, которые могут быть проведены по одному из следующих вариантов:

Понижение порядка . Делается замена переменных. Например, для функции двух переменных это y=x , в итоге получаем функцию одного переменного x . Далее исследуется поведение функции на прямых y=x и y=-x . Если в первом случае функция в исследуемой точке будет иметь минимум, а в другом случае максимум (или наоборот), то исследуемая точка представляет собой седловую точку .
Нахождение собственных значений гессиана. Если все значения положительные, функция в исследуемой точке имеет минимум, если все отрицательные – имеется максимум.
Исследование функции f(x) в окрестности точки ε. Переменные x заменяются на x 0 +ε. Далее необходимо доказать, что функция f(x 0 +ε) от одной переменной ε, либо больше нуля (тогда x 0 точка минимума), либо меньше нуля (тогда x 0 точка максимума).

Примечание . Чтобы найти обратный гессиан достаточно найти обратную матрицу .

Пример №1 . Какие из следующих функций являются выпуклыми или вогнутыми: f(x) = 8x 1 2 +4x 1 x 2 +5x 2 2 .
Решение . 1. Найдем частные производные.

2. Решим систему уравнений.
-4x 1 +4x 2 +2 = 0
4x 1 -6x 2 +6 = 0
Получим:
а) Из первого уравнения выражаем x 1 и подставляем во второе уравнение:
x 2 = x 2 + 1 / 2
-2x 2 +8 = 0
Откуда x 2 = 4
Данные значения x 2 подставляем в выражение для x 1 . Получаем: x 1 = 9 / 2
Количество критических точек равно 1.
M 1 (9 / 2 ;4)
3. Найдем частные производные второго порядка.

4. Вычислим значение этих частных производных второго порядка в критических точках M(x 0 ;y 0).
Вычисляем значения для точки M 1 (9 / 2 ;4)

Строим матрицу Гессе:

D 1 = a 11 < 0, D 2 = 8 > 0
Поскольку диагональные миноры имеют различные знаки, то о выпуклости или вогнутости функции ничего сказать нельзя.

Квадратичные формы

В матричной записи квадратичная форма имеет вид f(Х) = Х Т AX, где

В самом деле

Например, запишем в матричном виде квадратичную форму .

Пусть матрица-столбец переменных X получена невырожденным линейным преобразовании матрицы-столбца Y, т.е. X = CY, где С - невырожденная матрица n-го порядка. Тогда квадратичная форма
f(X) = Х T АХ = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Например, найдем квадратичную форму f(y 1 , y 2), полученную из квадратичной формы f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 линейным преобразованием .

Квадратичная форма называется канонической (имеет канонический вид ), если все ее коэффициенты a ij = 0 при i ≠ j, т.е.
f(х 1 , х 2 ,...,х n) = a 11 x 1 2 + a 22 x 2 2 + … + a nn x n 2 = .

Ее матрица является диагональной.

Например, приведем к каноническому виду квадратичную форму
f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 .

Для этого вначале выделим полный квадрат при переменной х 1:

f(х 1 , х 2 , х 3) = 2(x 1 2 + 2х 1 х 2 + х 2 2) - 2х 2 2 - 3х 2 2 – х 2 х 3 = 2(x 1 + х 2) 2 - 5х 2 2 – х 2 х 3 .

Теперь выделяем полный квадрат при переменной х 2:

f(х 1 , х 2 , х 3) = 2(x 1 + х 2) 2 – 5(х 2 2 – 2* х 2 *(1/10)х 3 + (1/100)х 3 2) - (5/100)х 3 2 =
= 2(x 1 + х 2) 2 – 5(х 2 – (1/10)х 3) 2 - (1/20)х 3 2 .

Тогда невырожденное линейное преобразование y 1 = x 1 + х 2 , y 2 = х 2 – (1/10)х 3 и y 3 = x 3 приводит данную квадратичную форму к каноническому виду f(y 1 , y 2 , y 3) = 2y 1 2 - 5y 2 2 - (1/20)y 3 2 .

Отметим, что канонический вид квадратичной формы определяется неоднозначно (одна и та же квадратичная форма может быть приведена к каноническому виду разными способами). Однако полученные различными способами канонические формы обладают рядом общих свойств. В частности, число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду (например, в рассмотренном примере всегда будет два отрицательных и один положительный коэффициент). Это свойство называют законом инерции квадратичных форм .

Убедимся в этом, по-другому приведя ту же квадратичную форму к каноническому виду. Начнем преобразование с переменной х 2:
f(х 1 , х 2 , х 3) = 2x 1 2 + 4х 1 х 2 - 3х 2 2 – х 2 х 3 = -3х 2 2 – х 2 х 3 + 4х 1 х 2 + 2x 1 2 = -3(х 2 2 –
- 2* х 2 ((1/6) х 3 + (2/3)х 1) +((1/6) х 3 + (2/3)х 1) 2) – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 =
= -3(х 2 – (1/6) х 3 - (2/3)х 1) 2 – 3((1/6) х 3 + (2/3)х 1) 2 + 2x 1 2 = f(y 1 , y 2 , y 3) = -3y 1 2 -
-3y 2 2 + 2y 3 2 , где y 1 = - (2/3)х 1 + х 2 – (1/6) х 3 , y 2 = (2/3)х 1 + (1/6) х 3 и y 3 = x 1 . Здесь положительный коэффициент 2 при y 3 и два отрицательных коэффициента (-3) при y 1 и y 2 (а при использовании другого способа мы получили положительный коэффициент 2 при y 1 и два отрицательных – (-5) при y 2 и (-1/20) при y 3).

Квадратичную форму f(X) называют положительно (отрицательно ) определенной , если при всех значениях переменных, не равных одновременно нулю, она положительна, т.е. f(X) > 0 (отрицательна, т.е.
f(X) < 0).

Например, квадратичная форма f 1 (X) = x 1 2 + х 2 2 - положительно определенная, т.к. представляет собой сумму квадратов, а квадратичная форма f 2 (X) = -x 1 2 + 2x 1 х 2 - х 2 2 - отрицательно определенная, т.к. представляет ее можно представить в виде f 2 (X) = -(x 1 - х 2) 2 .

Главным (угловым) минором k-го порядка матрицы А n-го порядка называют определитель матрицы, составленный из первых k строк и столбцов матрицы А ().

Например, исследуем на знакоопределенность квадратичную форму f(х 1 , х 2) = 2x 1 2 + 4х 1 х 2 + 3х 2 2 .

= (2 - l)*
*(3 - l) – 4 = (6 - 2l - 3l + l 2) – 4 = l 2 - 5l + 2 = 0; D = 25 – 8 = 17;
. Следовательно, квадратичная форма – положительно определенная.

Способ 2. Главный минор первого порядка матрицы А D 1 = a 11 = 2 > 0. Главный минор второго порядка D 2 = = 6 – 4 = 2 > 0. Следовательно, по критерию Сильвестра квадратичная форма – положительно определенная.

Исследуем на знакоопределенность другую квадратичную форму, f(х 1 , х 2) = -2x 1 2 + 4х 1 х 2 - 3х 2 2 .

Способ 1. Построим матрицу квадратичной формы А = . Характеристическое уравнение будет иметь вид = (-2 - l)*
*(-3 - l) – 4 = (6 + 2l + 3l + l 2) – 4 = l 2 + 5l + 2 = 0; D = 25 – 8 = 17;
. Следовательно, квадратичная форма – отрицательно определенная.

Положительно определенные квадратичные формы

Определение . Квадратичная форма от n неизвестных называется положительно определенной , если ее ранг равен положительному индексу инерции и равен числу неизвестных.

Теорема. Квадратичная форма положительно определена тогда и только тогда, когда на любом ненулевом наборе значений переменных принимает положительные значения.

Доказательство. Пусть квадратичная форманевырожденным линейным преобразованием неизвестных

приведена к нормальному виду

Для любого ненулевого набора значений переменных хотя бы одно из чисел отлично от нуля, т.е. . Необходимость теоремы доказана.

Предположим, что квадратичная форма принимает положительные значения на любом ненулевом наборе переменных, но ее положительный индекс инерции Невырожденным линейным преобразованием неизвестных

приведем ее к нормальному виду. Без ограничения общности можно считать, что в этом нормальном виде квадрат последней переменной либо отсутствует, либо входит в нее со знаком минус, т.е. , где или . Предположим, что – ненулевой набор значений переменных , полученный в результате решения системы линейных уравнений

В этой системе число уравнений равно числу переменных и определитель системы отличен от нуля. По теореме Крамера система имеет единственное решение, и оно ненулевое. Для этого набора . Противоречие с условием. Приходим к противоречию с предположением, что и доказывает достаточность теоремы.

С помощью этого критерия нельзя по коэффициентам установить, положительно ли определена квадратичная форма. Ответ на такой вопрос дает другая теорема, для формулировки которой введем еще одно понятие. Главные диагональные миноры матрицы – это миноры, расположенные в ее левом верхнем углу:

, , , … , .

Теорема. Квадратичная форма положительно определена тогда и только тогда, когда все ее главные диагональные миноры положительны.

Доказательство проведем методом полной математической индукции по числу n переменных квадратичной формы f.

Гипотеза индукции. Предположим, что для квадратичных форм с числом переменных меньшим n утверждение верно.

Рассмотрим квадратичную форму от n переменных. Соберем в одну скобку все слагаемые, содержащие . Оставшиеся слагаемые образуют квадратичную форму от переменных. По гипотезе индукции для нее утверждение верно.

Предположим, что квадратичная форма положительно определена. Тогда и квадратичная форма положительно определена. Если предположим, что это не так, то найдется ненулевой набор значений переменных , для которого и, соответственно, , а это противоречит тому, что квадратичная форма положительно определена. По гипотезе индукции все главные диагональные миноры квадратичной формы положительны, т.е. все первые главные миноры квадратичной формы f положительны. Последний главный минор квадратичной формы – этоопределитель ее матрицы. Этот определитель положителен, так как его знак совпадает со знаком матрицы ее нормального вида, т.е. со знаком определителя единичной матрицы.

Пусть все главные диагональные миноры квадратичной формы положительны, Тогда положительны все главные диагональные миноры квадратичной формы из равенства . По гипотезе индукции квадратичная форма положительно определена, поэтому существует невырожденное линейное преобразование переменных которое приводит форму к виду суммы квадратов новых переменных . Это линейное преобразование можно дополнить до невырожденного линейного преобразования всех переменных полагая . Квадратичная форма этим преобразованием приводится к виду

Найти нормальный вид квадратичных форм примеры. Квадратичные формы.Знакоопределённость форм. Критерий Сильвестра

Критерии определенности матрицы (теорема Сильвестра)

Квадратичные формы

Положительно определенные квадратичные формы