Аннотация: Данная лекция рассматривает основные методы решения задач многомерной оптимизации, в частности, такие как метод Хука – Дживса, метод Нелдера – Мида, метод полного перебора (метод сеток), метод покоординатного спуска, метод градиентного спуска.
До сих пор мы обсуждали одномерные задачи оптимизации, в которых целевая функция зависела только от одного аргумента. Однако подавляющее число реальных задач оптимизации, представляющих практический интерес, являются многомерными: в них целевая функция зависит от нескольких аргументов, причем иногда их число может быть весьма большим.
Математическая постановка таких задач аналогична их постановке в одномерном случае: ищется наименьшее (наибольшее) значение целевой функции, заданной на некотором множестве G возможных значений ее аргументов.
Как и в одномерном случае, характер задачи и соответственно возможные методы решения существенно зависят от той информации о целевой функции, которая нам доступна в процессе ее исследования. В одних случаях целевая функция задается аналитической формулой, являясь при этом дифференцируемой функцией. Тогда можно вычислить ее частные производные , получить явное выражение для градиента, определяющего в каждой точке направления возрастания и убывания функции, и использовать эту информацию для решения задачи. В других случаях никакой формулы для целевой функции нет, а имеется лишь возможность определить ее значение в любой точке рассматриваемой области (с помощью расчетов, в результате эксперимента и т.д.). В таких задачах в процессе решения мы фактически можем найти значения целевой функции лишь в конечном числе точек, и по этой информации требуется приближенно установить ее наименьшее значение для всей области.
1. Метод Хука – Дживса
Этот метод был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу.
Описание этой процедуры представлено ниже:
А . Выбрать начальную базисную точку b 1 и шаг длиной h j для каждой переменной x j , j = 1, 2, ..., n . В приведенной ниже программе для каждой переменной используется шаг h , однако указанная выше модификация тоже может оказаться полезной.
Б . Вычислить f(x) в базисной точке b 1 с целью получения сведений о локальном поведении функции f(x) . Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции. Функция f(x) в базисной точке b 1 находится следующим образом:
1. Вычисляется значение функции f(b 1) в базисной точке b 1 .
2. Каждая переменная по очереди изменяется прибавлением длины шага.
Таким образом, мы вычисляем значение функции f(b 1 + h 1 e 1) , где e 1 - единичный вектор в направлении оси х 1 . Если это приводит к уменьшению значения функции, то b 1 заменяется на b 1 + h 1 e 1 . В противном случае вычисляется значение функции f(b 1 – h 1 e 1) , и если ее значение уменьшилось, то b 1 заменяем на b 1 -h 1 e 1 . Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b 1 остается неизменной и рассматриваются изменения в направлении оси х 2 , т.е. находится значение функции f(b 1 + h 2 e 2) и т.д. Когда будут рассмотрены все n переменные, мы будем иметь новую базисную точку b 2 .
3. Если b 2 = b 1 , т.е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b 1 , но с уменьшенной длиной шага. На практике удовлетворительным является уменьшение шага (шагов) в десять раз от начальной длины.
4. Если , то производится поиск по образцу.
В . При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:
1. Разумно двигаться из базисной точки b 1 в направлении b 2 - b 1 , поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца
| (1.1) |
Правила ввода функций :
Например, x 1 2 +x 1 x 2 , записываем как x1^2+x1*x2Метод Хука-Дживса
относятся к категории эвристических методов (методам прямого поиска). Методы прямого поиска используют не менее n независимых направлений, где n -размерность вектора.
Элементарным примером метода, реализующего процедуру рекурсивного перебора на множестве направлений поиска, является метод циклического изменения переменных - каждый раз меняется только одна переменная. Затем вдоль каждого из координатных направлений последовательно проводится поиск точки экстремума на основе методов одномерной минимизации. Однако, если линии уровня ЦФ имеют овражный характер, то процедура поиска становится неэффективной и даже может привести к отсутствию сходимости к точке локального extr , если изменение координатных направлений поиска осуществляется в циклическом порядке (показано Пауэллом).
Модифицированный метод Хука-Дживса
позволяет существенно ускорить сходимость за счет того обстоятельства, что поиск периодически проводится в направлении d i =x i -x i -1 .
По существу процедура Хука–Дживса представляет собой комбинацию двух поисков:
а) исследующий поиск
(для выявления характера локального поведения ЦФ и определения направления движения вдоль "оврагов") с циклическим изменением переменных;
б) ускоряющий поиск по образцу
с использованием определенных эвристических правил.
Исследующий поиск.
Выбирается некоторая исходная точка x 0 . Задается величина шага ∆ i , которая может быть различной для разных координатных направлений и изменяться в процессе поиска.
Если значение ЦФ в пробной точке меньше значения ЦФ в исходной точке, то шаг поиска успешный. В противном случае из исходной точки делается шаг в противоположном направлении. После перебора всех n координат исследующий поиск завершается. Полученная точка называется базовой.
Поиск по образцу.
Осуществляется шаг из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой. Новая точка образца определяется по формуле:
x p k +1 =x k +(x k -x k -1).
Как только движение по образцу не приводит к уменьшению ЦФ, точка x p k +1 фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением ЦФ, чем в точке x k , то она рассматривается как новая базовая точка x k +1 . Но если исследующий поиск неудачен, то следует вернуться в точку x k и провести исследующий поиск с целью выявления нового направления минимизации. В конечном итоге возникает ситуация, когда такой поиск не приводит к успеху. В этом случае уменьшается шаг путем введения коэффициента α и возобновляется исследующий поиск.
Если исследуемая функция имеет овражный вид, то предпочтительнее использовать метод Хука-Дживса, а не метод Нелдера-Мида, так как в первом методе мы можем регулировать шаг в направлении убывания функции, в то время как во втором методе мы этого сделать не можем.
Схема алгоритма Хука–Дживса
Введем следующие обозначения: x k - текущая базовая точка; x k -1 - предыдущая базовая точка; x p k +1 - точка, построенная при движении по образцу; x k +1 - следующая (новая) базовая точка.Критерий останова: |∆x|≤ε.
Шаг 1. Определить начальную точку x 0 ; приращения (шаги) ∆ i ; коэффициент уменьшения шага α>1; параметр окончания поиска ε<1.
Шаг 2. Провести исследующий поиск.
Шаг 3. Был ли исследующий поиск удачным (найдена ли точка с меньшим значением ЦФ)?
Да: переход на Шаг 5. Нет: продолжить, т.е. переход на Шаг 4.
Шаг 4. Проверка на окончание поиска. Выполняется ли неравенство |Δx| ≤ ε? Да: окончание поиска, т.е. текущая точка аппроксимирует точку экстремума x * .
Нет: уменьшить приращение ∆ i /α; i=1,2,..,n. Переход на Шаг2.
Шаг 5. Провести поиск по образцу: x p k +1 =x k +(x k -x k -1).
Шаг 6. Провести исследующий поиск, используя точку x p k +1 в качестве временной базовой точки. Пусть в результате получена точка x k +1 .
Шаг 7. Выполняется ли неравенство: f(x k +1) < f(x k)?
Да: положить x k -1 = x k ; x k = x k +1 . Переход на Шаг 5.
Нет: переход на Шаг 4. Hooke - Jeeves ) так же, как и алгоритм Нелдера - Мида , служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две фазы: исследующий поиск и поиск по образцу (Pattern search).
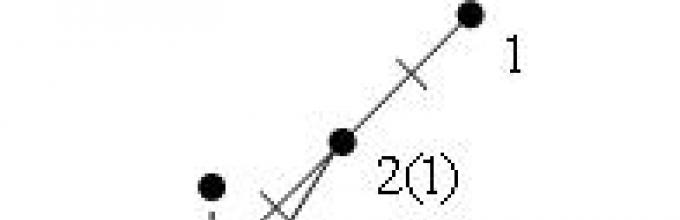
На начальном этапе задаётся стартовая точка (обозначим её 1) и шаги h i по координатам. Затем замораживаем значения всех координат кроме 1-й, вычисляем значения функции в точках x 0 +h 0 и x 0 -h 0 (где x 0 - первая координата точки, а h 0 - соответственно значение шага по этой координате) и переходим в точку с наименьшим значением функции. В этой точке замораживаем значения всех координат кроме 2-й, вычисляем значения функции в точках x 1 +h 1 и x 1 -h 1 , переходим в точку с наименьшим значением функции и т. д. для всех координат. В случае, если для какой-нибудь координаты значение в исходной точке меньше, чем значения для обоих направлений шага, то шаг по этой координате уменьшается. Когда шаги по всем координатам h i станут меньше соответствующих значений e i , алгоритм завершается, и точка 1 признаётся точкой минимума.
Иллюстрация первого этапа для двух координат:
Таким образом, проведя исследующий поиск по всем координатам, мы получим новую точку с наименьшим значением функции в окрестности (обозначим её 2). Теперь можно осуществлять переход ко 2 фазе алгоритма.
На этапе поиска по образцу откладывается точка 3 в направлении от 1 к 2 на том же расстоянии. Её координаты получаются по формуле x ¯ 3 = x ¯ 1 + λ (x ¯ 2 − x ¯ 1) {\displaystyle {\overline {x}}_{3}={\overline {x}}_{1}+\lambda ({\overline {x}}_{2}-{\overline {x}}_{1})} , где x i - точка с номером i, λ - параметр алгоритма, обычно выбирающийся равным 2. Затем в новой точке 3 проводится исследующий поиск, как на 1 фазе алгоритма, за исключением того, что шаг на этой фазе не уменьшается. Если на этой фазе в результате исследующего поиска удалось получить точку 4, отличную от точки 3, то точку 2 переобозначим на 1, а 4 на 2 и повторим поиск по образцу. В случае если не удаётся найти точку 4, отличную от точки 3, то точку 2 переобозначим на точку 1 и повторим 1-ю фазу алгоритма - исследующий поиск.
Иллюстрация второго этапа для двух координат:
В скобках отмечены имена точек после переобозначения. На иллюстрации хорошо заметно, как алгоритм корректирует своё направление в зависимости от найденных значений функции.
Энциклопедичный YouTube
-
1 / 3
Просмотров:
Лекция 6
Метод Хука и Дживса
Этот метод можно рассматривать как модификацию метода Гаусса-
Зейделя.



Рассмотрим простейшую модификацию метода Хука и Дживса на примере функции F = f (x 1, x 2)=(x 1+ x 2) 2 +(x 2-1) 2




Метод вращающихся координат Розенброка
Идея Розенброка - устранить ограничения покоординатного поиска и метода Хука-Дживса на возможные изменения переменных, которые в этих методах могли изменяться только в направлениях, параллельных осям координат. В методе Розенброка шаги поиска могут производиться вдоль направлений координатных осей, которые могут вращаться в пространстве. (т.е.движение может быть и по диагонали).
Первоначально оси выбираются совпадающими с осями координат пространства оптимизации. Затем вдоль каждой из осей делается шаг определенной длины. Если шаг был успешен, то длина шага увеличивается и попытка повторяется до тех пор, пока не последует неудача. Если первоначальный шаг был неудачен, то длина шага уменьшается и попытка повторятся до тех пор, пока не будет получено улучшение функции. Как только будет выявлена ситуация, когда значение функции не меняется, а необходимая точность не достигнута, то координатные оси поворачиваются с помощью процедуры ортогонализации . Такой процесс повторяется до тех пор, пока не будет выполнено условие останова. Например, улучшение значения функции станет малым или перемещение на нескольких шагах подряд будет невелико.
Однако имеется дополнительный недостаток - процедура ортогонализации очень дорого стоит и в смысле количества операций, производимых с системой координат, и в смысле необходимой памяти, которой требуется уже порядка n 2 , а не n , как в методе Хука-Дживса. Это значит, что даже в случае относительно “дешевой” целевой функции вычислительные затраты на ортогонализацию оказываются значительными в сравнении с общими затратами. Кроме того, размерность решаемых задач ограничивается требуемым объемом памяти.
Существует несколько модификаций алгоритма Розенброка, главная из которых состоит в отказе от постоянной длины шага и замене на процедуру масштабирования длины шага в зависимости от успешности поиска в данном направлении.
Поиск экстремума методом Нелдера-Мида
Основан на построении многогранника с вершинами на каждом шаге поиска, где количество переменных целевой функции. В начале поиска эти вершины выбирают произвольно, на последующих шагах выбор подчинен правилам метода.
Рассмотрим эти правила на примере двумерной задачи оптимизации. Так как количество переменных две то многогранник имеет 2+1 три вершины, т.е. это треугольник. Выбраны вершины исходного треугольника: , Новая вершина находится на луче, проведенном из худшей вершины (из вершины с наибольшим значением целевой функции) через центр тяжести многогранника, причем рекомендуется выбирать на расстоянии от, равном. Новая вершина заменяет худшую вершину. Если оказывается, что имеет лучшее значение целевой функции среди вершин многогранника, то расстояние увеличивают. На рисунке именно эта ситуация имеет место и увеличение дает точку. В новом многограннике с вершинами, худшей является вершина, аналогично получают вершину, затем вершину и т.д. Если новая вершина окажется худшей, то в многограннике нужно сохранить лучшую вершину, а длины всех ребер уменьшить, например вдвое (стягивание многогранника к лучшей вершине). Поиск прекращается при выполнении условия уменьшения размеров многогранника до некоторого предела.
Методы первого порядка
Метод градиентного спуска
В природе мы нередко наблюдаем явления, сходные с решением задачи на нахождение минимума. К ним относится, в частности, стекание воды с берега котлована на дно. Упростим ситуацию, считая, что берега котлована “унимодальны”, т.е. они гладкие и не содержат локальных углублений или выступов. Тогда вода устремится вниз в направлении наибольшей крутизны берега в каждой точке.
Переходя на математический язык, заключаем, что направление наискорейшего спуска соответствует направлению наибольшего убывания функции. Из курса математики известно, что направление наибольшего возрастания функции двух переменных u=f (x , y ) характеризуется ее градиентом
где e 1 , e 2 - единичные векторы (орты) в направлении координатных осей. Следовательно, направление, противоположное градиентному, укажет путь, ведущий вниз вдоль наиболее крутой линии. Методы, основанные на выборе пути оптимизации с помощью градиента, называются градиентными .
Идея метода градиентного спуска состоит в следующем. Выбираем некоторую начальную точку и вычисляем в ней градиент рассматриваемой функции. Делаем шаг в направлении, обратном градиентному. В результате приходим в точку, значение функции в которой обычно меньше первоначального. Если это условие не выполнено, т. е. значение функции не изменилось либо даже возросло, то нужно уменьшить шаг. В новой точке процедуру повторяем: вычисляем градиент и снова делаем шаг в обратном к нему направлении. Процесс продолжается до получения наименьшего значения целевой функции. Момент окончания поиска наступит тогда, когда движение из полученной точки с любым шагом приводит к возрастанию значения целевой функции. Строго говоря, если минимум функции достигается внутри рассматриваемой области, то в этой точке градиент равен нулю, что также может служить сигналом об окончании процесса оптимизации.
Формально поиск новой точки приближения к минимальной точке можно представить как

Очевидно, что в зависимости от выбора параметра λ траектории спуска будут существенно различаться. При большом значе-нии λ траектория спуска будет представлять собой колебательный про-цесс, а при слишком больших процесс может расходиться. При выборе малых траектория спуска будет плавной, но и процесс будет сходиться очень медленно.

В описанном методе требуется вычислять на каждом шаге оптимизации градиент целевой функции. Формулы для частных производных можно получить в явном виде лишь в том случае, когда целевая функция задана аналитически. В противном случае эти производные вычисляются с помощью численного дифференцирования:


При использовании градиентного спуска в задачах оптимизации основной объем вычислений приходится обычно на вычисление градиента целевой функции в каждой точке траектории спуска. Поэтому целесообразно уменьшить количество таких точек без ущерба для самого решения. Это достигается в некоторых методах, являющихся модификациями градиентного спуска. Одним из них является
Метод наискорейшего спуска.
Согласно этому методу, после определения в начальной точке направления, противоположного градиенту целевой функции, в этом направлении делают не один шаг, а двигаются до тех пор, пока целевая функция убывает, достигая таким образом минимума в некоторой точке. В этой точке снова определяют направление спуска (с помощью градиента) и ищут новую точку минимума целевой функции и т. д. В этом методе спуск происходит гораздо более крупными шагами и градиент функции вычисляется в меньшем числе точек.
Проиллюстрирую метод наискорейшего спуска на рисунке для случая функции двух переменных z = f(x,y) и отметим некоторые его геометрические особенности.

Во-первых, легко показать, что градиент функции перпендикулярен касательной к линии уровня в данной точке. Следовательно, в градиентных методах спуск происходит по нормали к линии уровня.
Во-вторых, в точке, в которой достигается минимум целевой функции вдоль направления, производная функции по этому направлению обращается в нуль. Но производная функции равна нулю по направлению касательной к линии уровня. Отсюда следует, что градиент целевой функции в новой точке перпендикулярен направлению одномерной оптимизации на предыдущем шаге, т. е. спуск на двух последовательных шагах производится во взаимно перпендикулярных направлениях.
Заметим, что метод наискорейшего спуска сводит многомерную задачу оптимизации к последовательности одномерных задач на каждом шаге оптимизации, как и в случае покоординатного спуска. Разница состоит в том, что здесь направление одномерной оптимизации определяется градиентом целевой функции, тогда как покоординатный спуск проводится на каждом шаге вдоль одного из координатных направлений.

Исследование оврагов
Все рассмотренные методы, как прямые, так и методы первого порядка страдают существенным недостатком они слабо применимы при наличии оврага на поверхности.
В случае оврага линии уровня сильно вытянуты в одном направлении и сплющены в другом. Они напоминают рельеф местности с оврагом. Действительно, попытаемся найти наименьшее значение такой функции с помощью градиентного спуска. Двигаясь все время в направлении антиградиента, мы быстро спустимся на дно "оврага" и, поскольку движение идет хотя и маленькими, но конечными шагами, проскочим его. Оказавшись на противоположной стороне "оврага" и вычислив там градиент функции, мы будем вынуждены развернуться почти на 180° и сделать один или несколько шагов в обратном направлении. При этом мы снова проскочим дно "оврага" и вернемся на его первоначальную сторону. Продолжая этот процесс, мы вместо того, чтобы двигаться по дну "оврага" в сторону его понижения, будем совершать зигзагообразные скачки поперек "оврага", почти не приближаясь к цели. Таким образом, в случае "оврага" (этот нематематический термин прочно закрепился в литературе) описанные выше методы спуска оказываются неэффективными.
Для борьбы с "оврагами" был предложен ряд специальных приемов. Один из них заключается в следующем. Совершают градиентный спуск на дно "оврага" и исследуют пошагово (без использования градиента) окрестность этой точки. Выбирают направление в котором наблюдается наиболее значительное снижение функции и делают вдоль нее большой (овражный) шаг. Из найденной точки снова спускаются на дно "оврага" и делают второй овражный шаг. В результате, двигаясь достаточно быстро вдоль "оврага", приближаемся к искомому наименьшему значению целевой функции. Такой метод достаточно эффективен для функций двух переменных, однако при большем числе переменных могут возникнуть трудности.
Проблема многоэкстремальности
Достаточно часто на практике имеются функции имеющие несколько минимумов.
На рисунке приведены линии уровня функции с двумя локальными минимумами в точках O 1 и O 2 . Такие функции принято называть многоэкстремальными. Сравнивая между собой значения функции в точках O 1 и O 2 f 1 =3 , f 2 =1 , находим, что наименьшее значение функция достигает в точке O 2 .
Представьте себе теперь, что, не имея перед глазами рисунка и не зная о многоэкстремальности функции, мы начали поиск наименьшего значения с помощью метода градиентного спуска из точки A 1 . Поиск приведет нас в точку O 1 , которую ошибочно можно принять за искомый ответ. С другой стороны, если мы начнем поиск с точки A 2 , то окажемся на правильном пути и быстро придем в точку O 2 .
Как бороться с многоэкстремальностью? Универсального ответа на этот вопрос нет. Самый простой прием состоит в том, что проводят поиск несколько раз, начиная его с разных точек. Если при этом получаются разные ответы, то сравнивают в них значения целевой функции и выбирают наименьшее. Расчеты останавливают после того, как несколько новых поисков не меняют полученного ранее результата. Выбор начальных точек поиска, обоснованность прекращения расчетов в значительной степени зависят от опыта и интуиции специалистов, решающих задачу.
Решение задач условной оптимизации методом Лагранжа
Особый интерес для практических задач оптимизации представляют задачи, в которых наряду с целевой функцией заданы ограничения. Задачи, имеющие ограничения значений переменных получили название задачи условной оптимизации. Задачи условной оптимизации не могут быть решены с использованием классических методов и для них были разработаны специальные методы. Одним из наиболее часто используемых методов является метод Лагранжа.
Решение задач условной оптимизации методом Лагранжа.
Пусть задана задача математического программирования: максимизировать функцию
Z = f (х 1 , х 2 , ..., х n) при ограничениях
g i (х 1 , х 2 , ..., х n ) = 0, i= 1, 2. ..., m
Основная идея метода заключается в переходе от задачи на условный экстремум исходной функции f (x) к задаче на безусловный экстремум некоторой специально построенной функции Лагранжа F .
С этой целью составим функцию
(2.7)
Где множитель Лагранжа.
Определим частные производные
И приравняем их нулю. В результате получим систему уравнений
Функция (2.7) называется функцией Лагранжа, а числа - множителями Лагранжа . Решая систему находим точки x 1 (0) , x 2 (0) , ..., x n (0) , λ 1 (0) , λ 2 (0) , ..., λ m (0) которые и определяют точки экстремума (в общем случае таких точек может быть несколько). Однако для того чтобы определить какой экстремум (мах или мин) нужно дополнительное исследование связанное с анализом значения функции в найденной точке.
Пример 1. Найти точку условного экстремума функции Z=x 1 x 2 +x 2 x 3 при ограничениях
Решение. Составим функцию Лагранжа
F (х 1 , х 2 , х 3 , λ 1 , λ 2 )= х 1 х 2 + х 2 х 3 + λ 1 (х 1 + х 2 -2)+ λ 2 (х 2 + х 3 -2)
и продифференцируем ее по переменным х 1 , х 2 , х 3 , λ 1 и λ 2 . Приравнивая полученные выражения нулю, получим следующую систему уравнений:
Из первого и третьего уравнения следует, что λ 1 = λ 2 = - х 2 ; тогда
Решая данную систему, получим: х 1 = х 2 = х 3 = 1, Z =2.
Для определения характера экстремума исследуем окрестность точки Z =2. С этой целью дадим приращения h 1, h 2, h 3 для точек х1, х2, х3.
Т.е новые точки имеют координаты 1+ h 1, 1+ h 2, 1+ h 3
Подставим эти значения в ограничения.
1+ h 1+1+ h 2=2
1+ h 2+1+ h 3=2
Т.е.
h 1+ h 2=0
h 2+ h 3=0
Или h 1=- h 2 и h 2=- h 3
Подставим значения новых точек в функцию
Ф=(1+ h 1)*(1+ h 2)+(1+ h 2)*(1+ h 3)
С учетом найденных значений h
Ф=2-2 h 1 2
Т.е окрестность точки экстремума меньше значения функции в этой точке, что свидетельствует, что это максимум.
Еще раз подчеркнем, что основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных средств решения проблемы.
Методы Хука-Дживса
1. Введение
2. Метод Хука-Дживса
4. Блок-схема данного метода
5. Блок-схема единичного исследования
6. Текст программы
7. Распечатка результатов работы программы
8. Литература
Введение
На разработку методов прямого поиска для определения минимума функций и переменных было затрачено много усилий. Методы прямого поиска являются методами, в которых используются только значения функции. Мы рассмотрим подробно лишь один из них. Практика показала, что этот метод эффективен и применим для широкого числа приложений.
Рассмотрим функцию двух переменных. Ее линии постоянного уровня 1
на рис. 1,

а минимум лежит в точке (x 1 * ,x 2 *). Простейшим методом поиска является метод покоординатного спуска. Из точки А мы производим поиск минимума вдоль направления оси и, таким образом, находим точку В, в которой касательная к линии постоянного уровня параллельна оси. Затем, производя поиск из точки В в направлении оси, получаем точку С, производя поиск параллельно оси, получаем точку D, и т. д. Таким образом, мы приходим к оптимальной точке. Очевидным образом эту идую можно применить для функций n-переменных.
Теоретически данный метод эффективен в случае единственного минимума функции. Но на практике он оказывается слишком медленным. Поэтому были разработаны более сложные методы, использующие больше информации на основании уже полученных значений функции.
Метод Хука-Дживса
Метод Хука-Дживса был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу. Он применяется для решения задачи минимизирования функции без учета ограничений.
Описание этой процедуры представлено ниже:
А. Выбрать начальную базисную точку b 1 и шаг длиной h 1 для каждой переменной x j , j = 1, 2,…, n. В приведенной ниже программе для каждой переменной используется шаг h , однако указанная выше модификация тоже может оказаться полезной.
Б. Вычислить f (х) в базисной точке b 1 с целью получения сведений о локальном поведении функции f (x). Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции. Функция f (x) в базисной точке b 1 , находится следующим образом:
1. Вычисляется значение функции f (b 1) в базисной точке b 1 .
2. Каждая переменная по очереди изменяется прибавлением длины шага. Таким образом, мы вычисляем значение функции f (b 1 +h 1 e 1), где e 1 – единичный вектор в направлении оси x 1 . Если это приводит к уменьшению значения функции, то b 1 заменяется на b 1 +h 1 e 1 . В противном случае вычисляется значение функции f (b 1 -h 1 e 1), и если ее значение уменьшилось, то b 1 заменяем на b 1 -h 1 e 1 . Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b 1 остается неизменной и рассматриваются изменения в направлении оси х 2 , т. е. находится значение функции f (b 1 +h 2 e 2) и т. д. Когда будут рассмотрены все n переменные, мы будем иметь новую базисную точку b 2 .
3. Если b 2 =b 1 , т. е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b 1 , но с уменьшенной длиной шага. На практике удовлетворительным является уменьшение шага (шагов) в десять раз от начальной длины.
4. Если b 2 b 1 , то производится поиск по образцу.
В. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:
3. Разумно двигаться из базисной точки b 2 в направлении b 2 -b 1 , поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца
P 1 =b 1 +2(b 2 -b 1) .
В общем случае
P i =b i +2(b i+1 -b i) .
2. Затем исследование следует продолжать вокруг точки Р 1 (Р i) .
3. Если наименьшее значение на шаге В, 2 меньше значения в базисной точке b 2 (в общем случае b i+1), то получают новую базисную точку b 3 (b i+2), после чего следует повторить шаг В, 1. В противном случае не производить поиск по образцу из точки b 2 (b i+1), а продолжить исследования в точке b 2 (b i+1).
Г. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до заданного малого значения.
Модифицированный метод Хука-Дживса
Этот метод нетрудно модифицировать и для учета ограничений.Было выдвинуто предложение, что для этого будет вполне достаточно при решении задачи минимизации присвоить целевой функции очень большое значение там,где ограничения нарушаются.К тому же такую идею просто реализовать с помощью програмирования.
Нужно проверить,каждая ли точка,полученная в процессе поиска, принадлежит области ограничений.Если каждая, то целевая функция вычисляется обычным путем. Если нет, то целевой функции присваивается очень большое значение. Таким образом, поиск будет осуществляться снова в допустимой области в направлении к минимальной точке внутри этой области.
В тексте прогаммы модифицированного метода прямого поиска Хука-Дживса сделана попытка реализовать такую процедуру. Рассматриваемая задача формулируется следующим образом:
минимизировать f


Текст программы
program HuDjMody;
(*** Модифицированный метод Хука-Дживса ***)
(*** (при наличии ограничений) ***)
label 0,1,2,3,4,5,6,7;
var k,h,z,ps,bs,fb,fi:real;
i,j,n,fe:integer;
x,y,b,p:array of real;
(*** Процедура,вычисляющая функцию ***)
procedure calculate;
z:=3*sqr(x)+(4*x*x)+(5*sqr(x));
if (x<0) or (x<0) or ((x+x)<4) then
fe:=fe+1; (*** Счетчик ***)
writeln("Модифицированный метод Хука-Дживса");
writeln("(при наличии ограничений)");
writeln("Введите число переменных:");
writeln("Введите начальную точку x1,x2,…,xN");
for i:=1 to n do
writeln("Введите длину шага");
for i:=1 to n do
writeln("Начальное значение функции", z:2:3);
for i:=1 to n do
writeln(x[i]:2:3);
(*** Исследование вокруг базисной точки ***)
0: x[j]:=y[j]+k;
if z if z writeln("Пробный шаг"," ", z:2:3); for i:=1 to n do writeln(x[i]:2:3); if j=n then goto 3; 3: if fi (*** После оператора 3,если функция не уменьшилась, ***) (*** произвести поиск по образцу ***) if (ps=1) and (bs=0) then (*** Но если исследование производилось вокруг точки ***) (*** шаблона PT,и уменьшение функции не было достигнуто,***) (*** то изменить базисную точку в операторе 4: ***) (*** в противном случае уменьшить длину шага в операторе***) 4: for i:=1 to n do writeln("Замена базисной точки"," ",z:2:3); for i:=1 to n do writeln(x[i]:1:3); (*** (следует за последним комментарием) ***) (*** и провести исследование вокруг новой базисной точки ***) writeln("Уменьшить длину шага"); if k<1e-08 then goto 7; (*** Если поиск незакончен,то произвести новое ***) (*** исследование вокруг новой базисной точки ***) (*** Поиск по образцу ***) 6: for i:=1 to n do p[i]:=2*y[i]-b[i]; writeln("Поиск по образцу"," ",z:2:3); for i:=1 to n do writeln(x[i]:2:3); (*** После этого произвести исследование вокруг ***) (*** последней точки образца ***) 7: writeln("Минимум найден"); for i:=1 to n do writeln("x(",i,")=",p[i]:2:3); writeln("Минимум функции равен"," ",fb:2:3); writeln("Количество вычислений функции равно"," ",fe); repeat until keypressed; Приведенная выше программа реализует описанную процедуру. Одной или двух точек бывает недостаточно для определения начальной точки. Первая точка всегда должна выбираться осмотрительно. ЭВМ работает только с ограниченной точностью, и ошибки могут накапливаться в процессе сложных вычислений, особенно если шаг имеет “неудобную” длину. (Обычно мы будем избегать “неудобной” длины, но программа должна быть работоспособна и в таких ситуациях.) Поэтому в строке, где выясняется вопрос об изменении базисной точки, мы избегаем уменьшения длины шага из-за накапливания ошибки введением длины шага, равной . Мы отслеживаем, где производится исследование – в базисной точке (В5 = 1, Р5 = 0) или в точке образца (В5 = 0, Р5 = 1). Как можно убедиться на практике, если не принимаются такие меры предосторожности даже программа с удовлетворительной логикой будет неработоспособна. В приведенной программе минимальная длина шага равна , но она может быть изменена. Для контроля за выполнением процедуры в программу введена печать промежуточных результатов. Для увеличения скорости счета могут быть удалены строки вывода подсказок и пояснений. Процедура calculate
вычисляет значение минимизируемой функции,в нашем случае: f
(x 1
,x 2) = 3x 1
2
+4x 1
x 2
+5x 2
2
, при ограничениях x 1
x 2
x 1
+x 2
. Минимум, равный 44, достигается в точке (3;1) при ограничении x 1
+x 2
=4. Для начальной точки (4;3) и при длине шага, равной единице, программой успешно решена задача минимизации. Ниже приведена распечатка результата работы программы: Модифицированный метод Хука-Дживса (при наличииограничений) Введите число переменных Введите длину шага Начальное значение функции 141.000 Пробный шаг 108.000 Пробный шаг 71.000 Пробный шаг 44.000 Пробный шаг 44.000 Поиск по образцу 1.70000000000001566Е+0038 Пробный шаг 48.000 Пробный шаг 48.000 Замена базисной точки 44.000 Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Пробный шаг 44.000 Пробный шаг 44.000 Уменьшить длину шага Минимум найден Минимум функции равен 44.000 Количество вычислений равно 74 Для начальной точки (3;4) и длины шага, равной единице, программой также успешно решена задача минимизации. Для начальной точки (5;6) и длины шага, равной единице, задача не решена, т.к. программа остановилась в точке (1;3) , т.е. на активном ограничении, и выдала неверный результат. Распечатка результата работы программы приведена ниже: Модифицированный метод Хука-Дживса (при наличииограничений) Введите число переменных Введите начальную точку х1,х2,…,хN Введите длину шага Начальное значение функции 375.000 Пробный шаг 324.000 Пробный шаг 253.000 Поиск по образцу 155.000 Пробный шаг 124.000 Пробный шаг 81.000 Поиск по образцу 1.70000000000001566Е+0038 Пробный шаг 1.70000000000001566Е+0038 Замена базисной точки 81.000 Пробный шаг 60.000 Пробный шаг 60.000 Поиск по образцу 1.70000000000001566Е+0038 Пробный шаг 60.000 Пробный шаг 60.000 Замена базисной точки 60.000 Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Пробный шаг 60.000 Пробный шаг 60.000 Уменьшить длину шага Минимум найден Минимум функции равен 60.000 Количество вычислений равно 89 Аналогичные неутешительные результаты были получены для начальной точки (5;6) и длины шага, равной 0.5 .Неверное решение было найдено в точке (1.5;2.5) . Для начальной точки (4;3) и длины шага, равной 0.5 ,программа работала нормально, но было получено неверное решение в точке (2.5;1.5) . Проблема понятна. С помощью данного метода невозможно двигаться вдоль границы области ограничений и сходимость достигается в первой же точке границы, где и находится решение. Общая задача оптимизации при наличии ограничений очень сложна и для получения практического метода решения требуются более изощренные процедуры, чем приведенная выше. Литература:
1. Б.Банди “Методы оптимизации” 2. Р.Хук, Т.А.Дживс “ Прямой поиск решения для числовых и статических проблем ”, 212-219 с., 1961 .