Математические методы исследования. Методическая разработка на тему: математические исследования на уроках математики. Резерв:начальный и конечный

Содержание статьи

МАТЕМАТИЧЕСКИЙ АНАЛИЗ, раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела.

Начало математическому анализу положил в 1665 И.Ньютон и (около 1675) независимо от него Г.Лейбниц, хотя важную подготовительную работу провели И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма (1601–1665), Дж.Валлис (1616–1703) и И.Барроу (1630–1677).

Чтобы сделать изложение более живым, мы будем прибегать к языку графиков. Поэтому читателю, возможно, будет полезно заглянуть в статью АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ , прежде чем приступать к чтению данной статьи.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

Касательные.

На рис. 1 показан фрагмент кривой y = 2x – x 2 , заключенный между x = –1 и x = 3. Достаточно малые отрезки этой кривой выглядят прямыми. Иначе говоря, если Р – произвольная точка этой кривой, то существует некоторая прямая, проходящая через эту точку и являющаяся приближением кривой в малой окрестности точки Р , причем чем меньше окрестность, тем лучше приближение. Такая прямая называется касательной к кривой в точке Р . Основная задача дифференциального исчисления заключается в построении общего метода, позволяющего находить направление касательной в любой точке кривой, в которой касательная существует. Нетрудно представить себе кривую с резким изломом (рис. 2). Если Р – вершина такого излома, то можно построить аппроксимирующую прямую PT 1 – справа от точки Р и другую аппроксимирующую прямую РТ 2 – слева от точки Р . Но не существует единственной прямой, проходящей через точку Р , которая одинаково хорошо приближалась к кривой в окрестности точки P как справа, так и слева, следовательно касательной в точке P не существует.

На рис. 1 касательная ОТ проведена через начало координат О = (0,0). Угловой коэффициент этой прямой равен 2, т.е. при изменении абсциссы на 1 ордината увеличивается на 2. Если x и y – координаты произвольной точки на ОТ , то, удаляясь от О на расстояние х единиц вправо, мы удаляемся от О на 2y единиц вверх. Следовательно, y /x = 2, или y = 2x . Это уравнение касательной ОТ к кривой y = 2x – x 2 в точке О .

Необходимо теперь объяснить, почему из множества прямых, проходящих через точку О , выбрана именно прямая ОТ . Чем же прямая с угловым коэффициентом 2 отличается от других прямых? Существует один простой ответ, и нам трудно удержаться от искушения привести его, используя аналогию с касательной к окружности: касательная ОТ имеет с кривой только одну общую точку, тогда как любая другая невертикальная прямая, проходящая через точку О , пересекает кривую дважды. В этом можно убедиться следующим образом.

Поскольку выражение y = 2x – x 2 можно получить вычитанием х 2 из y = 2x (уравнения прямой ОТ ), то значения y для графика оказываются меньше знаний y для прямой во всех точках, за исключением точки x = 0. Следовательно, график всюду, кроме точки О , расположен ниже ОТ , и эта прямая и график имеют только одну общую точку. Кроме того, если y = mx – уравнение какой-нибудь другой прямой, проходящей через точку О , то обязательно найдутся две точки пересечения. Действительно, mx = 2x – x 2 не только при x = 0, но и при x = 2 – m . И только при m = 2 обе точки пересечения совпадают. На рис. 3 показан случай, когда m меньше 2, поэтому справа от О возникает вторая точка пересечения.

То, что ОТ – единственная невертикальная прямая, проходящая через точку О и имеющая с графиком лишь одну общую точку, не самое главное ее свойство. Действительно, если мы обратимся к другим графикам, то вскоре выяснится, что отмеченное нами свойство касательной в общем случае не выполняется. Например, из рис. 4 видно, что вблизи точки (1,1) график кривой y = x 3 хорошо аппроксимируется прямой РТ , имеющей однако, с ним более одной общей точки. Тем не менее, нам хотелось бы считать РТ касательной к этому графику в точке Р . Поэтому необходимо найти какой-то иной способ выделения касательной, чем тот, который так хорошо послужил нам в первом примере.

Предположим, что через точку О и произвольную точку Q = (h ,k ) на графике кривой y = 2x – x 2 (рис. 5) проведена прямая (называемая секущей). Подставляя в уравнение кривой значения x = h и y = k , получаем, что k = 2h – h 2 , следовательно, угловой коэффициент секущей равен

При очень малых h значение m близко к 2. Более того, выбирая h достаточно близким к 0, мы можем сделать m сколь угодно близким к 2. Можно сказать, что m «стремится к пределу», равному 2, когда h стремится к нулю, или что предел m равен 2 при h , стремящемся к нулю. Символически это записывается так:

Тогда касательная к графику в точке О определяется как прямая, проходящая через точку О , с угловым коэффициентом, равным этому пределу. Такое определение касательной применимо в общем случае.

Покажем преимущества этого подхода еще на одном примере: найдем угловой коэффициент касательной к графику кривой y = 2x – x 2 в произвольной точке P = (x ,y ), не ограничиваясь простейшим случаем, когда P = (0,0).

Пусть Q = (x + h , y + k ) – вторая точка на графике, находящаяся на расстоянии h справа от Р (рис. 6). Требуется найти угловой коэффициент k /h секущей PQ . Точка Q находится на расстоянии

над осью х .

Раскрывая скобки, находим:

Вычитая из этого уравнения y = 2x – x 2 , находим расстояние по вертикали от точки Р до точки Q :

Следовательно, угловой коэффициент m секущей PQ равен

Теперь, когда h стремится к нулю, m стремится к 2 – 2x ; последнюю величину мы и примем за угловой коэффициент касательной PT . (Тот же результат получится, если h принимает отрицательные значения, что соответствует выбору точки Q слева от P .) Заметим, что при x = 0 полученный результат совпадает с предыдущим.

Выражение 2 – 2x называется производной от 2x – x 2 . В старину производную также называли «дифференциальным отношением» и «дифференциальным коэффициентом». Если выражением 2x – x 2 обозначить f (x ), т.е.

то производную можно обозначить

Для того, чтобы узнать угловой коэффициент касательной к графику функции y = f (x ) в какой-нибудь точке, необходимо подставить в f ў (x ) соответствующее этой точке значение х . Таким образом, угловой коэффициент f ў (0) = 2 при х = 0, f ў (0) = 0 при х = 1 и f ў (2) = –2 при х = 2.

Производную также обозначают у ў , dy /dx , D х y и Dу .

Тот факт, что кривая y = 2x – x 2 вблизи данной точки практически неотличима от ее касательной в этой точке, позволяет говорить об угловом коэффициенте касательной как об «угловом коэффициенте кривой» в точке касания. Такие образом, мы можем утверждать, что угловой коэффициент рассматриваемой нами кривой имеет в точке (0,0) угловой коэффициент 2. Можно также сказать, что при x = 0 скорость изменения y относительно x равна 2. В точке (2,0) угловой коэффициент касательной (и кривой) равен –2. (Знак минус означает, что при возрастании x переменная y убывает.) В точке (1,1) касательная горизонтальна. Мы говорим, что кривая y = 2x – x 2 имеет в этой точке стационарное значение.

Максимумы и минимумы.

Мы только что показали, что кривая f (x ) = 2x – x 2 стационарна в точке (1,1). Так как f ў (x ) = 2 – 2x = 2(1 – x ), ясно, что при x , меньших 1, f ў (x ) положительна, и, следовательно, y возрастает; при x , больших 1, f ў (x ) отрицательна, и поэтому y убывает. Таким образом, в окрестности точки (1,1), обозначенной на рис. 6 буквой М , значение у растет до точки М , стационарно в точке М и убывает после точки М . Такая точка называется «максимумом», поскольку значение у в этой точке превосходит любые его значения в достаточно малой ее окрестности. Аналогично, «минимум» определяется как точка, в окрестности которой все значения y превосходят значение у в самой этой точке. Может также случиться, что хотя производная от f (x ) в некоторой точке и обращается в нуль, ее знак в окрестности этой точки не меняется. Такая точка, не являющаяся ни максимумом, ни минимумом, называется точкой перегиба.

В качестве примера найдем стационарную точку кривой

Производная этой функции равна

и обращается в нуль при x = 0, х = 1 и х = –1; т.е. в точках (0,0), (1, –2/15) и (–1, 2/15). Если х чуть меньше –1, то f ў (x ) отрицательна; если х чуть больше –1, то f ў (x ) положительна. Следовательно, точка (–1, 2/15) – максимум. Аналогично, можно показать, что точка (1, –2/15) – минимум. Но производная f ў (x ) отрицательна как до точки (0,0), так и после нее. Следовательно, (0,0) – точка перегиба.

Проведенное исследование формы кривой, а также то обстоятельство, что кривая пересекает ось х при f (x ) = 0 (т.е. при х = 0 или ) позволяют представить ее график примерно так, как показано на рис. 7.

В общем, если исключить необычные случаи (кривые, содержащие прямолинейные отрезки или бесконечное число изгибов), существуют четыре варианта взаимного расположения кривой и касательной в окрестности точки касания Р . (См . рис. 8, на котором касательная имеет положительный угловой коэффициент.)

1) По обе стороны от точки Р кривая лежит выше касательной (рис. 8,а ). В этом случае говорят, что кривая в точке Р выпукла вниз или вогнута.

2) По обе стороны от точки Р кривая расположена ниже касательной (рис. 8,б ). В этом случае говорят, что кривая выпукла вверх или просто выпукла.

3) и 4) Кривая располагается выше касательной по одну сторону от точки Р и ниже – по другую. В этом случае Р – точка перегиба.

Сравнивая значения f ў (x ) по обе стороны от Р с ее значением в точке Р , можно определить, с каким из этих четырех случаев приходится иметь дело в конкретной задаче.

Приложения.

Все изложенное выше находит важные приложения в различных областях. Например, если тело брошено вертикально вверх с начальной скоростью 200 футов в секунду, то высота s , на которой они будут находиться через t секунд по сравнению с начальной точкой составит

Действуя так же, как в рассмотренных нами примерах, находим

эта величина обращается в нуль при с. Производная f ў (x ) положительна до значения с и отрицательна по истечении этого времени. Следовательно, s возрастает до , затем становится стационарной, а после убывает. Таково общее описание движения брошенного вверх тела. Из него мы узнаем, когда тело достигает высшей точки. Далее, подставляя t = 25/4 в f (t ), мы получаем 625 футов, максимальную высоту подъема. В данной задаче f ў (t ) имеет физический смысл. Эта производная показывает скорость, с которой тело движется в момент времени t .

Рассмотрим теперь приложение другого типа (рис. 9). Из листа картона площадью 75 см 2 требуется изготовить коробку с квадратным дном. Каковы должны быть размеры этой коробки, чтобы она имела максимальный объем? Если х – сторона основания коробки и h – ее высота, то объем коробки равен V = x 2 h , а площадь поверхности равна 75 = x 2 + 4xh . Преобразуя уравнение, получаем:

Производная от V оказывается равной

и обращается в нуль при х = 5. Тогда

и V = 125/2. График функции V = (75x – x 3)/4 показан на рис. 10 (отрицательные значения х опущены как не имеющие физического смысла в данной задаче).

Производные.

Важная задача дифференциального исчисления – создание методов, позволяющих быстро и удобно находить производные. Например, несложно посчитать, что

(Производная от постоянной, разумеется, равна нулю.) Нетрудно вывести общее правило:

где n – любое целое число или дробь. Например,

(На этом примере видно, как полезны дробные показатели степени.)

Приведем некоторые важнейшие формулы:

Существуют также следующие правила: 1) если каждая из двух функций g (x ) и f (x ) имеет производные, то производная их суммы равна сумме производных этих функций, а производная разности равна разности производных, т.е.

2) производная произведения двух функций вычисляется по формуле:

3) производная отношения двух функций имеет вид

4) производная функции, умноженной на константу, равна константе, умноженной на производную этой функции, т.е.

Часто бывает, что значения функции приходится вычислять поэтапно. Например, чтобы вычислить sin x 2 , нам необходимо сначала найти u = x 2 , а затем уже вычислить синус числа u . Производную таких сложных функций мы находим с помощью так называемого «цепного правила»:

В нашем примере f (u ) = sin u , f ў (u ) = cos u , следовательно,

Эти и другие, аналогичные им, правила позволяют сразу же выписывать производные многих функций.

Линейные аппроксимации.

То обстоятельство, что, зная производную, мы можем во многих случаях заменить график функции вблизи некоторой точки ее касательной в этой точке, имеет огромное значение, поскольку с прямыми легче работать.

Эта идея находит непосредственное приложение в вычислении приближенных значений функций. Например, довольно трудно вычислить значение при x = 1,033. Но можно воспользоваться тем, что число 1,033 близко к 1 и что . Вблизи x = 1 мы можем заменить график кривой касательной, не совершая при этом сколько-нибудь серьезной ошибки. Угловой коэффициент такой касательной равен значению производной (x 1/3)ў = (1/3)x –2/3 при x = 1, т.е. 1/3. Так как точка (1,1) лежит на кривой и угловой коэффициент касательной к кривой в этой точке равен 1/3, уравнение касательной имеет вид

На этой прямой при х = 1,033

Полученное значение y должно быть очень близко к истинному значению y ; и, действительно, оно лишь на 0,00012 больше истинного. В математическом анализе разработаны методы, позволяющие повышать точность такого рода линейных приближений. Эти методы обеспечивают надежность наших приближенных вычислений.

Только что описанная процедура наводит на мысль об одном полезном обозначении. Пусть P – точка, соответствующая на графике функции f переменной х , и пусть функция f (x ) дифференцируема. Заменим график кривой вблизи точки Р касательной к нему, проведенной в этой точке. Если х изменить на величину h , то ордината касательной изменится на величину h Ч f ў (x ). Если h очень мало, то последняя величина служит хорошим приближением к истинному изменению ординаты y графика. Если вместо h мы напишем символ dx (это не произведение!), а изменение ординаты y обозначим dy , то получим dy = f ў (x )dx , или dy /dx = f ў (x ) (см . рис. 11). Поэтому вместо Dy или f ў (x ) для обозначения производной часто используется символ dy /dx . Удобство этого обозначения зависит главным образом от явного появления цепного правила (дифференцирования сложной функции); в новых обозначениях эта формула выглядит следующим образом:

где подразумевается, что у зависит от u , а u в свою очередь зависит от х .

Величина dy называется дифференциалом у ; в действительности она зависит от двух переменных, а именно: от х и приращения dx . Когда приращение dx очень мало, величина dy близка к соответствующему изменению величины y . Но предполагать, что приращение dx мало, нет необходимости.

Производную функции y = f (x ) мы обозначили f ў (x ) или dy /dx . Часто оказывается возможным взять производную от производной. Результат называется второй производной от f (x ) и обозначается f ўў (x ) или d 2 y /dx 2 . Например, если f (x ) = x 3 – 3x 2 , то f ў (x ) = 3x 2 – 6x и f ўў (x ) = 6x – 6. Аналогичные обозначения используются и для производных более высокого порядка. Однако, чтобы избежать большого количества штрихов (равного порядку производной) четвертую производную (например) можно записать как f (4) (x ), а производную n -го порядка как f (n ) (x ).

Можно показать, что кривая в точке выпукла вниз, если вторая производная положительна, и выпукла вверх, если вторая производная отрицательна.

Если функция имеет вторую производную, то изменение величины y , соответствующее приращению dx переменной х , можно приближенно вычислить по формуле

Это приближение, как правило, лучше, чем то, которое дает дифференциал f ў (x )dx . Оно соответствует замене части кривой уже не прямой, а параболой.

Если у функции f (x ) существуют производные более высоких порядков, то

Остаточный член имеет вид

где x – некоторое число между x и x + dx . Приведенный выше результат называется формулой Тейлора с остаточным членом. Если f (x ) имеет производные всех порядков, то обычно R n ® 0 при n ® Ґ .

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

Площади.

При изучении площадей криволинейных плоских фигур открываются новые аспекты математического анализа. Такого рода задачи пытались решать еще древние греки, для которых определение, например, площади круга было одной из труднейших задач. Больших успехов в решении этой проблемы добился Архимед, которому также удалось найти площадь параболического сегмента (рис. 12). С помощью весьма сложных рассуждений Архимед доказал, что площадь параболического сегмента составляет 2/3 от площади описанного прямоугольника и, следовательно, в данном случае равна (2/3)(16) = 32/3. Как мы увидим в дальнейшем, этот результат можно легко получить методами математического анализа.

Предшественники Ньютона и Лейбница, главным образом Кеплер и Кавальери, решали задачи о вычислении площадей криволинейных фигур с помощью метода, который трудно назвать логически обоснованным, но который оказался чрезвычайно плодотворным. Когда же Валлис в 1655 соединил методы Кеплера и Кавальери с методами Декарта (аналитической геометрией) и воспользовался только что зародившейся алгеброй, сцена для появления Ньютона была полностью подготовлена.

Валлис разбивал фигуру, площадь которой требовалось вычислить, на очень узкие полоски, каждую из которых приближенно считал прямоугольником. Затем он складывал площади аппроксимирующих прямоугольников и в простейших случаях получал величину, к которой стремилась сумма площадей прямоугольников, когда число полосок стремилось к бесконечности. На рис. 13 показаны прямоугольники, соответствующие некоторому разбиению на полоски площади под кривой y = x 2 .

Основная теорема.

Великое открытие Ньютона и Лейбница позволило исключить трудоемкий процесс перехода к пределу суммы площадей. Это было сделано благодаря новому взгляду на понятие площади. Суть в том, что мы должны представить площадь под кривой как порожденную ординатой, движущейся слева направо и спросить, с какой скоростью изменяется заметаемая ординатами площадь. Ключ к ответу на этот вопрос мы получим, если рассмотрим два частных случая, в которых площадь заранее известна.

Начнем с площади под графиком линейной функции y = 1 + x , поскольку в этом случае площадь можно вычислить с помощью элементарной геометрии.

Пусть A (x ) – часть плоскости, заключенная между прямой y = 1 + x и отрезком OQ (рис. 14). При движении QP вправо площадь A (x ) возрастает. С какой скоростью? Ответить на этот вопрос нетрудно, так как мы знаем, что площадь трапеции равна произведению ее высоты на полусумму оснований. Следовательно,

Скорость изменения площади A (x ) определяется ее производной

Мы видим, что A ў (x ) совпадает с ординатой у точки Р . Случайно ли это? Попробуем проверить на параболе, изображенной на рис. 15. Площадь A (x ) под параболой у = х 2 в интервале от 0 до х равна A (x ) = (1 / 3)(x )(x 2) = x 3 /3. Скорость изменения этой площади определяется выражением

которое в точности совпадает с ординатой у движущейся точки Р .

Если предположить, что это правило выполняется в общем случае так, что

есть скорость изменения площади под графиком функции y = f (x ), то этим можно воспользоваться для вычислений и других площадей. На самом деле, соотношение A ў (x ) = f (x ) выражает фундаментальную теорему, которую можно было бы сформулировать следующим образом: производная, или скорость изменения площади как функции от х , равна значению функции f (x ) в точке х .

Например, чтобы найти площадь под графиком функции y = x 3 от 0 до х (рис. 16), положим

Возможный ответ гласит:

так как производная от х 4 /4 действительно равна х 3 . Кроме того, A (x ) равна нулю при х = 0, как и должно быть, если A (x ) действительно является площадью.

В математическом анализе доказывается, что другого ответа, кроме приведенного выше выражения для A (x ), не существует. Покажем, что это утверждение правдоподобно с помощью следующего эвристического (нестрогого) рассуждения. Предположим, что существует какое-либо второе решение В (x ). Если A (x ) и В (x ) «стартуют» одновременно с нулевого значения при х = 0 и все время изменяются с одинаковой скоростью, то их значения ни при каком х не могут стать различными. Они должны всюду совпадать; следовательно, существует единственное решение.

Как можно обосновать соотношение A ў (x ) = f (x ) в общем случае? На этот вопрос можно ответить, лишь изучая скорость изменения площади как функции от х в общем случае. Пусть m – наименьшее значение функции f (x ) в интервале от х до (x + h ), а M – наибольшее значение этой функции в том же интервале. Тогда приращение площади при переходе от х к (x + h ) должно быть заключено между площадями двух прямоугольников (рис. 17). Основания обоих прямоугольников равны h . Меньший прямоугольник имеет высоту m и площадь mh , больший, соответственно, М и Mh . На графике зависимости площади от х (рис. 18) видно, что при изменении абсциссы на h , значение ординаты (т.е. площадь) увеличивается на величину, заключенную между mh и Mh . Угловой коэффициент секущей на этом графике находится между m и M . Что происходит, когда h стремится к нулю? Если график функции y = f (x ) непрерывен (т.е. не содержит разрывов), то и М , и m стремятся к f (x ). Следовательно, угловой коэффициент A ў (x ) графика площади как функции от х равен f (x ). Именно к такому заключению и требовалось придти.

Лейбниц предложил для площади под кривой y = f (x ) от 0 до а обозначение

При строгом подходе этот так называемый определенный интеграл должен быть определен как предел некоторых сумм на манер Валлиса. Учитывая полученный выше результат, ясно, что этот интеграл вычисляется при условии, что мы можем найти такую функцию A (x ), которая обращается в нуль при х = 0 и имеет производную A ў (x ), равную f (x ). Нахождение такой функции принято называть интегрированием, хотя уместнее эту операцию было бы называть антидифференцированием, имея в виду, что она является в некотором смысле обратной дифференцированию. В случае многочлена интегрирование выполняется просто. Например, если

в чем нетрудно убедиться, продифференцировав A (x ).

Чтобы вычислить площадь А 1 под кривой y = 1 + x + x 2 /2, заключенную между ординатами 0 и 1, мы просто записываем

и, подставляя х = 1, получаем A 1 = 1 + 1 / 2 + 1 / 6 = 5 / 3 . Площадь A (x ) от 0 до 2 равна A 2 = 2 + 4 / 2 + 8 / 6 = 16 / 3 . Как видно из рис. 19, площадь, заключенная между ординатами 1 и 2, равна A 2 – A 1 = 11 / 3 . Обычно она записывается в виде определенного интеграла

Объемы.

Аналогичные рассуждения позволяют удивительно просто вычислять объемы тел вращения. Продемонстрируем это на примере вычисления объема шара, еще одной классической задачи, которую древним грекам, с помощью известных им методов, удалось решить с великим трудом.

Повернем часть плоскости, заключенной внутри четверти круга радиуса r , на угол 360° вокруг оси х . В результате мы получим полушарие (рис. 20), объем которого обозначим V (x ). Требуется определить, с какой скоростью возрастает V (x ) с увеличением x . Переходя от х к х + h , нетрудно убедиться в том, что приращение объема меньше, чем объем p (r 2 – x 2)h кругового цилиндра радиуса и высотой h , и больше, чем объем p [r 2 – (x + h ) 2 ]h цилиндра радиуса и высотой h . Следовательно, на графике функции V (x ) угловой коэффициент секущей заключен между p (r 2 – x 2) и p [r 2 – (x + h ) 2 ]. Когда h стремится к нулю, угловой коэффициент стремится к

При x = r мы получаем

для объема полушария, и, следовательно, 4p r 3 /3 для объема всего шара.

Аналогичный метод позволяет находить длины кривых и площади искривленных поверхностей. Например, если a (x ) – длина дуги PR на рис. 21, то наша задача состоит в вычислении a ў(x ). Воспользуемся на эвристическом уровне приемом, который позволяет не прибегать к обычному предельному переходу, необходимому при строгом доказательстве результата. Предположим, что скорость изменения функции а (x ) в точке Р такая же, какой она была бы при замене кривой ее касательной PT в точке P . Но из рис. 21 непосредственно видно, при шаге h вправо или влево от точки х вдоль РТ значение а (x ) меняется на

Следовательно, скорость изменения функции a (x ) составляет

Чтобы найти саму функцию a (x ), необходимо лишь проинтегрировать выражение, стоящее в правой части равенства. Оказывается, что для большинства функций выполнить интегрирование довольно трудно. Поэтому разработка методов интегрального исчисления составляет большую часть математического анализа.

Первообразные.

Каждую функцию, производная которой равна данной функции f (x ), называют первообразной (или примитивной) для f (x ). Например, х 3 /3 – первообразная для функции х 2 , так как (x 3 /3)ў = x 2 . Разумеется, х 3 /3 – не единственная первообразная функции х 2 , так как x 3 /3 + C также является производной для х 2 при любой константе С . Однако мы в дальнейшем условимся опускать такие аддитивные постоянные. В общем случае

где n – положительное целое число, так как (x n + 1/(n + 1))ў = x n . Соотношение (1) выполняется в еще более общем смысле, если n заменить любым рациональным числом k , кроме –1.

Произвольную первообразную функцию для заданной функции f (x ) принято называть неопределенным интегралом от f (x ) и обозначать его в виде

Например, так как (sin x )ў = cos x , справедлива формула

Во многих случаях, когда существует формула для неопределенного интеграла от заданной функции, ее можно найти в многочисленных широко публикуемых таблицах неопределенных интегралов. Табличными являются интегралы от элементарных функций (в их число входят степени, логарифмы, показательная функция, тригонометрические функции, обратные тригонометрические функции, а также их конечные комбинации, получаемые с помощью операций сложения, вычитания, умножения и деления). С помощью табличных интегралов можно вычислить интегралы и от более сложных функций. Существует много способов вычисления неопределенных интегралов; наиболее распространенный из них метод подстановки или замены переменной. Он состоит в том, что если мы хотим в неопределенном интеграле (2) заменить x на некоторую дифференцируемую функцию x = g (u ), то, чтобы интеграл не изменился, надо x заменить на g ў (u )du . Иначе говоря, справедливо равенство

(подстановка 2x = u , откуда 2dx = du ).

Приведем еще один метод интегрирования – метод интегрирования по частям. Он основан на известной уже формуле

Проинтегрировав левую и правую части, и учитывая, что

Эта формула называется формулой интегрирования по частям.

Пример 2. Требуется найти . Так как cos x = (sin x )ў , мы можем записать, что

Из (5), полагая u = x и v = sin x , получаем

А поскольку (–cos x )ў = sin x мы находим, что и

Следует подчеркнуть, что мы ограничились лишь весьма кратким введением в весьма обширный предмет, в котором накоплены многочисленные остроумные приемы.

Функции двух переменных.

В связи с кривой y = f (x ) мы рассмотрели две задачи.

1) Найти угловой коэффициент касательной к кривой в данной точке. Эта задача решается вычислением значения производной f ў (x ) в указанной точке.

2) Найти площадь под кривой над отрезком оси х , ограниченную вертикальными линиями х = а и х = b . Эта задача решается вычислением определенного интеграла .

Каждая из этих задач имеет аналог в случае поверхности z = f (x ,y ).

1) Найти касательную плоскость к поверхности в данной точке.

2) Найти объем под поверхностью над частью плоскости ху , ограниченной кривой С , а сбоку – перпендикулярами к плоскости xy , проходящими через точки граничной кривой С (см . рис. 22).

Следующие примеры показывают, как решаются эти задачи.

Пример 4. Найти касательную плоскость к поверхности

в точке (0,0,2).

Плоскость определена, если заданы две лежащие в ней пересекающиеся прямые. Одну из таких прямых (l 1) мы получим в плоскости xz (у = 0), вторую (l 2) – в плоскости yz (x = 0) (см . рис. 23).

Прежде всего, если у = 0, то z = f (x ,0) = 2 – 2x – 3x 2 . Производная по х , обозначаемая f ў x (x ,0) = –2 – 6x , при х = 0 имеет значение –2. Прямая l 1 , задаваемая уравнениями z = 2 – 2x , у = 0 – касательная к С 1 , линии пересечения поверхности с плоскостью у = 0. Аналогично, если х = 0, то f (0,y ) = 2 – y – y 2 , и производная по у имеет вид

Так как f ў y (0,0) = –1, кривая С 2 – линия пересечения поверхности с плоскостью yz – имеет касательную l 2 , задаваемую уравнениями z = 2 – y , х = 0. Искомая касательная плоскость содержит обе прямые l 1 и l 2 и записывается уравнением

Это – уравнение плоскости. Кроме того, мы получаем прямые l 1 и l 2 , полагая, соответственно, у = 0 и х = 0.

В том, что уравнение (7) действительно задает касательную плоскость, на эвристическом уровне можно убедиться, если заметить, что это уравнение содержит члены первого порядка, входящие в уравнение (6), и что члены второго порядка можно представить в виде –. Так как это выражение отрицательно при всех значениях х и у , кроме х = у = 0, поверхность (6) всюду лежит ниже плоскости (7), кроме точки Р = (0,0,0). Можно сказать, что поверхность (6) выпукла вверх в точке Р .

Пример 5. Найти касательную плоскость к поверхности z = f (x ,y ) = x 2 – y 2 в начале координат 0.

На плоскости у = 0 имеем: z = f (x ,0) = x 2 и f ў x (x ,0) = 2x . На С 1 , линии пересечения, z = x 2 . В точке O угловой коэффициент равен f ў x (0,0) = 0. На плоскости х = 0 имеем: z = f (0,y ) = –y 2 и f ў y (0,y ) = –2y . На С 2 , линии пересечения, z = –y 2 . В точке O угловой коэффициент кривой С 2 равен f ў y (0,0) = 0. Так как касательные к С 1 и С 2 являются осями х и у , касательная плоскость, содержащая их, есть плоскость z = 0.

Однако в окрестности начала координат наша поверхность не находится по одну сторону от касательной плоскости. Действительно, кривая С 1 всюду, за исключением точки 0, лежит выше касательной плоскости, а кривая С 2 – соответственно ниже ее. Поверхность пересекает касательную плоскость z = 0 по прямым у = х и у = –х . Про такую поверхность говорят, что она имеет седловую точку в начале координат (рис. 24).

Частные производные.

В предыдущих примерах мы использовали производные от f (x ,y ) по х и по у . Рассмотрим теперь такие производные в более общем плане. Если у нас имеется функция двух переменных, например, F (x ,y ) = x 2 – xy , то мы можем определить в каждой точке две ее «частные производные», одну – дифференцируя функцию по х и фиксируя у , другую – дифференцируя по у и фиксируя х . Первая из этих производных обозначается как f ў x (x ,y ) или ¶ f /¶ x ; вторая – как f f ў y . Если обе смешанные производные (по х и у , по у и х ) непрерывны, то ¶ 2f /¶ x ¶ y = ¶ 2f /¶ y ¶ x ; в нашем примере ¶ 2f /¶ x ¶ y = ¶ 2f /¶ y ¶ x = –1.

Частная производная f ў x (x ,y ) указывает скорость изменения функции f в точке (x ,y ) в направлении возрастания х , а f ў y (x ,y ) – скорость изменения функции f в направлении возрастания у . Скорость изменения функции f в точке (х ,у ) в направлении прямой, составляющей угол q с положительным направлением оси х , называется производной от функции f по направлению; ее величина представляет собой комбинацию двух частных производных от функции f в касательной плоскости почти равно (при малых dx и dy ) истинному изменению z на поверхности, но вычислить дифференциал обычно бывает легче.

Уже рассмотренная нами формула из метода замены переменной, известная как производная сложной функции или цепное правило, в одномерном случае, когда у зависит от х , а х зависит от t , имеет вид:

Для функций двух переменных аналогичная формула имеет вид:

Понятия и обозначения частного дифференцирования нетрудно обобщить на более высокие размерности. В частности, в случае если поверхность задана неявно уравнением f (x ,y ,z ) = 0, уравнению касательной плоскости к поверхности можно придать более симметричную форму: уравнение касательной плоскости в точке (x (x 2 /4)], затем интегрируется по х от 0 до 1. Окончательный результат равен 3/4.

Формулу (10) можно интерпретировать и как так называемый двойной интеграл, т.е. как предел суммы объемов элементарных «клеток». Каждая такая клетка имеет основание D x D y и высоту, равную высоте поверхности над некоторой точкой прямоугольного основания (см . рис. 26). Можно показать, что обе точки зрения на формулу (10) эквивалентны. Двойные интегралы используются для нахождения центров тяжести и многочисленных моментов, встречающихся в механике.

Более строгое обоснование математического аппарата.

До сих пор мы излагали понятия и методы математического анализа на интуитивном уровне и, не колеблясь, прибегали к геометрическим фигурам. Нам осталось кратко рассмотреть более строгие методы, появившиеся в 19 и 20-м столетиях.

В начале 19 в., когда эпоха штурма и натиска в «создании математического анализа» завершилась, на первый план вышли вопросы его обоснования. В работах Абеля, Коши и ряда других выдающихся математиков были точно определены понятия «предела», «непрерывной функции», «сходящегося ряда». Это было необходимо для того, чтобы внести логический порядок в основание математического анализа с тем, чтобы сделать его надежным инструментом исследования. Потребность в тщательном обосновании стала еще более очевидной после открытия в 1872 Вейерштрассом всюду непрерывных, но нигде не дифференцируемых функций (график таких функций в каждой своей точке имеет излом). Этот результат произвел ошеломляющее впечатление на математиков, поскольку явно противоречил их геометрической интуиции. Еще более поразительным примером ненадежности геометрической интуиции стала построенная Д.Пеано непрерывная кривая, целиком заполняющая некоторый квадрат, т.е. проходящая через все его точки. Эти и другие открытия вызвали к жизни программу «арифметизации» математики, т.е. придания ей большей надежности путем обоснования всех математических понятий с помощью понятия числа. Почти пуританское воздержание от наглядности в работах по основаниям математики имело свое историческое оправдание.

По современным канонам логической строгости недопустимо говорить о площади под кривой y = f (x ) и над отрезком оси х , даже если f – непрерывная функция, не определив предварительно точный смысл термина «площадь» и не установив, что определенная таким образом площадь действительно существует. Эта задача была успешно решена в 1854 Б.Риманом, который дал точное определение понятия определенного интеграла. С тех пор идея суммирования, стоящая за понятием определенного интеграла, была предметом многих глубоких исследований и обобщений. В результате сегодня удается придать смысл определенному интегралу, даже если подынтегральная функция является повсюду разрывной. Новые понятия интегрирования, в создание которых большой вклад внес А.Лебег (1875–1941) и другие математики, приумножили мощь и красоту современного математического анализа.

Вряд ли было бы уместно входить в детали всех этих и других понятий. Ограничимся лишь тем, что приведем строгие определения предела и определенного интеграла.

В заключение скажем, что математический анализ, являясь крайне ценным инструментом в руках ученого и инженера, и сегодня привлекает внимание математиков как источник плодотворных идей. В то же время современное развитие как будто свидетельствует и о том, что математический анализ все более поглощается такими доминирующими в 20 в. разделами математики, как абстрактная алгебра и топология.

Одним из показателей зрелости науки считается использование ею математических методов исследования. Такие методы применяются в криминалистике издавна. В сущности, уже упоминавшийся такой общий метод познания, как измерение, есть гносеологически обобщенное понятие любого математического метода. Однако когда мы говорим о "математизации" криминалистики, то имеем в виду современные математические методы исследования, состоящие из операций неизмеримо более сложных, нежели простое сравнение объекта с мерой.

С начала 60-х годов в криминалистической литературе получает широкое признание как принципиальная возможность использования математических методов в криминалистических научных исследованиях, так и необходимость их применения для решения задач криминалистической экспертизы, в том числе и задачи идентификации. Рассматривая эту проблему в разных аспектах, криминалисты неизменно подчеркивали, что применение математических методов исследования открывает новые возможности в развитии как криминалистической науки, так и практики доказывания, а сама постановка этой проблемы свидетельствует о достижении криминалистикой такого уровня развития, когда она, как и другие развитые науки, испытывает потребность в тех точных методах познания своего предмета, которые может предоставить ей современная математика.

Процесс "математизации" криминалистики в настоящее время протекает в трех направлениях. Первое из них - это общетеоретическое направление.

В общетеоретическом плане процесс "математизации" поставил перед криминалистами задачу принципиального обоснования возможностей применения математических методов исследования и определения тех областей науки, при разработке которых эти методы могут дать наиболее эффективные результаты. В литературе данное направление представлено работами В. А. Пошкявичуса, Н. С. Полевого, А. А. Эйсмана, Н. А. Селиванова, З. И. Кирсанова, Л. Г. Эджубова и других авторов. Основные выводы, которые можно сделать после ознакомления с их исследованиями, сводятся к следующему:

1. Процесс "математизации" криминалистики есть естественный процесс, обусловленный современным этапом развития этой науки и математических методов исследования, приобретающих в силу этого все более универсальный характер. Использование математико-кибернетических методов исследования в криминалистике принципиально допустимо; их применение в доказывании нельзя рассматривать как использование специальных знаний, если речь идет о количественных характеристиках и элементарных математических методах; в тех случаях, когда математические методы используются для описания, обоснования или анализа явлений, познание которых осуществляется с помощью специальных знаний, применение этих методов охватывается понятием применения в судопроизводстве специальных познаний.

2. Использование математико-кибернетических методов исследования возможно в целях:

А) совершенствования методики криминалистической экспертизы, что в итоге приведет к расширению ее возможностей;

Б) научного анализа процесса доказывания и разработки рекомендаций по применению теории вероятностей и математической статистики, математической логики, исследования операций и теории игр в следственной практике.

В исследованиях общетеоретического направления получили свое отражение и два других направления процесса "математизации" криминалистики: использование математических методов в криминалистической экспертизе и при анализе процесса доказывания в целом.

Второе направление рассматриваемого процесса - использование математических методов для разработки проблем теории криминалистической идентификации и ее практических приложений и проблем криминалистической экспертизы, а в итоге - и проблем судебной экспертизы в целом . Суть этого направления и пути использования результатов математизации охарактеризованы А. Р. Шляховым: "Роль математических методов в судебной экспертизе двояка: с одной стороны, они выступают в качестве составной части функционирования ЭВМ в виде программных комплексов решения задач и ИПС, с другой стороны, они могут использоваться самостоятельно, без ЭВМ и обеспечивать полное либо частичное решение задач судебной экспертизы. Математические методы давно и прочно вошли в методики производства экспертиз, например, трасологических, баллистических, почерковедческих, автотехнических и др. ... Математические методы полезны при обработке результатов измерений, аналитического сравнения и как критерий достаточности выявленной совокупности признаков для индивидуализации объекта, оценки полноты ее в целях отождествления".

Это направление развивается наиболее интенсивно как непосредственно отвечающее потребностям судебно-экспертной практики. Еще в 1969 г. А. Р. Шляхов отмечал, что математические методы заняли одно из главных мест в системе методов, общих для всех стадий экспертного исследования и различных видов криминалистических экспертиз. В 1977 г. методы прикладной математики и программно-математические методы применения ЭВМ по предложенной А. И. Винбергом и А. Р. Шляховым классификации методов экспертного исследования были отнесены к числу общих (общепознавательных) методов. С конца 60-х гг. идет интенсивный поиск точек приложения математико-кибернетических методов практически во всех видах судебных экспертиз, предпринимаются попытки инвентаризации применяемых методов.

В результате интенсивного изучения проблемы использования математических методов в научных и экспертных исследованиях был поставлен вопрос о пределах их применения. Г. Л. Грановский отметил две точки зрения: одни возлагают надежды в области совершенствования экспертизы только на применение методов точных наук, другие более осторожно подходят к этому вопросу и указывают на пределы возможностей использования современной математики. Именно их позиция представляется более близкой к правильному пониманию проблемы". По его мнению, существуют естественные ограничения, "которые природа объектов экспертизы налагает на возможности использования для их исследования математических методов... Применение количественных методов в любой экспертизе теоретически допустимо, но практически еще мало известно, какие признаки и в каких пределах поддаются математическому описанию и оценке, какие результаты можно ожидать от использования для их исследования математических методов". Современная экспертная практика идет по пути решения этой двуединой задачи: определение точек приложения математических методов, и затем уже их практическое использование.

В настоящее время математические методы наиболее активно применяются при решении задач судебно-почерковедческой экспертизы, САТЭ, а также КЭМВИ; при этом они не только используются при проведении судебно-экспертного исследования (в процессе получения информации об объекте судебной экспертизы), но и являются средством решения судебно- экспертной задачи на основе информации об объекте. При этом наибольшую доказательственную ценность составляет количественная информация, что подтверждают исследования, связанные с решением задачи установления ФКВ объектов волокнистой природы (В.А. Пучков, В. З. Поляков, 1986) на основе результатов аналитического исследования микрочастиц волокон (когда после проведения информационного поиска по массиву волокон, исследованных в экспертизах, задача принятия решения по результатам конкретного аналитического исследования сводится к теоретико-вероятностной задаче), с применением вероятностно-статистической модели (Л. А. Гегечкори, 1985) к решению задачи криминалистической идентификации по признакам состава и строения (модель может быть использована как на предварительной стадии, так и на стадиях сравнительного исследования и синтезирующей; ядром модели являются статистические критерии, использующиеся на стадии сравнительного исследования и в зависимости от которых организуется статистический анализ информационных фондов, необходимый при работе модели на других стадиях решения задачи), с разработкой математической модели задач дифференциации подлинных подписей и неподлинных, выполненных с подражанием после предварительной тренировки (С. А. Атаходжаев и др., 1984). Отметим также разработку математических моделей задачи о наезде ТС на пешехода в условиях ограниченной видимости и некоторые подходы к применению математических методов в задачах судебно-фоноскопической экспертизы.

Опыт использования математических методов в судебной экспертизе свидетельствует о том, что необходимо четко разграничивать применение математических методов для обработки информации, получаемой в процессе изучения объектов судебной экспертизы, и разработку математических моделей для решения судебно-экспертных задач на основе результатов исследования. Если первый аспект не является специфически криминалистическим (ибо исследование объекта судебной экспертизы ведется естественнонаучными методами), то второй имеет особую криминалистическую природу. Она предстает в снятом виде, когда мы располагаем уже математической моделью для решения типовой судебно-экспертной задачи, однако, если не отвлекаться от процесса разработки математической модели, криминалистическая природа ее обнаруживается со всей очевидностью. В самом деле, разработка математических моделей для типовых судебно-экспертных задач всегда инициируется потребностью решения конкретных, индивидуально определенных задач. Специалист-математик в тесном контакте с судебным экспертом выделяет наиболее существенные количественные закономерности, которые дают возможность разработать математическую модель не только для конкретной судебно-экспертной задачи, но и для целого типа задач. В этом и заключен глубокий смысл математизации их решения. Математические методы в судебной экспертизе являются не только (и не столько) методами изучения объектов, получения информации о них (каковы, например, физические и химические методы), но и методами решения судебно-экспертных задач на основе результатов исследования.

Третье направление математизации криминалистических научных исследований - применение математических методов для решения проблем криминалистической тактики и методики. В литературе оно представлено работами А. А. Эйсмана, И. М. Лузгина, Л. Г. Видонова, Н.А. Селиванова и др. Уже первые исследования в этой области показали ограниченность приложения математических методов к решению проблем тактики и методики.

А. А. Эйсман справедливо отметил, что "судебное доказывание не может быть описано с помощью средств традиционной логики, прежде всего, потому, что все акты доказывания, как простые, так и сложные, носят не только качественный характер (да/нет), но и количественный (более надежно, менее надежно). Именно эта оценочная, количественная сторона создает главные трудности для моделирования... Отсутствуют какие бы то ни было средства и возможности показать абсолютный уровень этой надежности, дать ей строгие количественные значения. Это вполне понятно, потому что мы не располагаем (и трудно с научной достоверностью предсказать, будем ли когда-нибудь располагать) методами количественной оценки улик. По-видимому, единственным средством получения таких количественных характеристик является статистическая обработка огромного числа событий и фактов, входящих в содержание доказательств. При этом речь идет о статистическом учете значения отдельных фактов (например, обнаружения поличного) в разных меняющихся условиях. Нетрудно представить почти беспредельный объем таких статистических исследований. В то же время, трудно судить и о практической эффективности результатов, если они будут получены." Именно поэтому А. А. Эйсман высказывал мнение, что в логике следствия из средств математической логики используются лишь некоторые формулы исчисления высказываний, которые "не образуют строгого исчисления, то есть законченного аппарата правил построения вывода, а играют вспомогательную роль". Это мнение поддерживал и И. М. Лузгин.

Н. А. Селиванов ограничил применение математических методов в области криминалистической тактики лишь измерением различных объектов и решением некоторых задач в процессе отдельных следственных действий, преимущественно при осмотре места происшествия: для определения неизвестного расстояния по двум известным, наклона линии полета брызг крови, размеров автомобильных шин по их следам, скорости движения автомобиля по тормозному пути и некоторых других. У И. М. Лузгина мы встречаем упоминание о логико-математическом моделировании, объектами которого, с его точки зрения, могут быть признаки спорных ситуаций, факты, образующие состав преступления, и связанные с ним обстоятельства, отношения между предметами и явлениями, признаки следов. Однако, кроме упоминания, никаких данных, подтверждающих реальную возможность такого моделирования, он не приводит.

Пионерами изучения возможности применения в криминалистической методике вероятностно-статистических методов можно считать З. И. Кирсанова и Н. А. Родионова. Первый определил основные направления применения статистических методов: для изучения способов совершения преступления, видов документов, подделываемых преступниками, предметов, используемых в качестве тайников, в целом для обобщения и изучения следственной практики и т. п.. Второй назвал те статистические методы, которые, по его мнению, могут быть применены при расследовании преступлений. Примером успешного применения вероятностно-статистических методов для определения зависимостей между элементами криминалистической характеристики умышленных убийств служат работы Л. Г. Видонова.

Предпринимаются попытки оценки при помощи вероятностно-статистических методов эффективности отдельных тактических приемов или их сочетаний в рамках специальных комплексов, эффективности тактических комбинаций (операций) по отдельным категориям преступлений.

Расширение сферы применения в криминалистике математических методов логически повлекло за собой исследование возможностей их использования для решения практических задач на базе компьютерных технологий. "Говоря о применении математических методов, хотелось бы подчеркнуть, что не следует противопоставлять их ЭВМ, - справедливо замечал уже в 1984 году в этой связи А. Р. Шляхов. - Математические и технико- криминалистические методы могут дополнять друг друга, взаимодействовать, а в ряде случаев функционировать параллельно. По своей сути и форме они не тождественны. Верно, что почти все достижимое математикой может решать и

ЭВМ (иногда даже лучше математиков), но без математиков ЭВМ бессильна". Такой областью правоохранительной практической деятельности, где применение ЭВМ оказалось наиболее перспективным, является судебная экспертиза.

Помимо экспертной практики, в криминалистике определились следующие направления использования кибернетических методов:

Извлечение информации о различных объектах, процессах и автоматизация ее первичной обработки;

Применение автоматических устройств и ЭВМ для срочной обработки информации и для получения производных параметров по фиксированной первичной информации;

Автоматизация процесса кодирования и сканирования информации;

Компьютерное распознавание образов;

Исследование математических моделей процесса доказывания.

Математические методы наиболее широко используются при проведении системных исследований. При этом решение практических задач математическими методами последовательно осуществляется по следующему алгоритму:

математическая формулировка задачи (разработки математической модели);

выбор метода проведения исследования полученной математической модели;

анализ полученного математического результата.

Математическая формулировка задачи обычно представляется в виде чисел, геометрических образов, функций, систем уравнений и т. п. Описание объекта (явления) может быть представлено с помощью непрерывной или дискретной, детерминированной или стохастической и другими математическими формами.

Математическая модель представляет собой систему математических соотношений (формул, функций, уравнений, систем уравнений), описывающих те или иные стороны изучаемого объекта, явления, процесса или объект (процесс) в целом.

Первым этапом математического моделирования является постановка задачи, определение объекта и целей исследования, задание критериев (признаков) изучения объектов и управления ими. Неправильная или неполная постановка задачи может свести на нет результаты всех последующих этапов.

Модель является результатом компромисса между двумя противоположными целями:

модель должна быть подробной, учитывать все реально существующие связи и участвующие в его работе факторы и параметры;

в то же время модель должна быть достаточно простой, чтобы можно было получить приемлемые решения или результаты в приемлемые сроки при определенных ограничениях на ресурсы.

Моделирование можно назвать приближенным научным исследованием. А степень его точности зависит от исследователя, его опыта, целей, ресурсов.

Допущения, принимаемые при разработке модели, являются следствием целей моделирования и возможностей (ресурсов) исследователя. Они определяются требованиями точности результатов, и как сама модель, являются результатом компромисса. Ведь именно допущения отличают одну модель одного и того же процесса от другой.

Обычно при разработке модели отбрасываются (не принимаются во внимание) несущественные факторы. Константы в физических уравнениях считаются постоянными. Иногда усредняются некоторые величины, изменяющиеся в процессе (например, температура воздуха может считаться неизменной за какой-то промежуток времени).

1. Процесс разработки модели

Это процесс последовательной (и возможно, неоднократной) схематизации или идеализации исследуемого явления.

Адекватность модели - это ее соответствие тому реальному физическому процессу (или объекту), который она представляет.

Для разработки модели физического процесса необходимо определить:

Иногда используется подход, когда применяется модель небольшой полноты, носящая вероятностный характер. Потом с помощью ЭВМ производится ее анализ и уточнение.

Проверка модели начинается и проходит в самом процессе ее построения, когда выбираются или устанавливаются те или иные взаимосвязи между ее параметрами, оцениваются принятые допущения. Однако после сформирования модели в целом надо проанализировать ее с некоторых общих позиций.

Математическая основа модели (т. е. математическое описание физических взаимосвязей) должна быть непротиворечивой именно с точки зрения математики: функциональные зависимости должны иметь те же тенденции изменения, что и реальные процессы; уравнения должны иметь область существования не менее диапазона, в котором проводится исследование; в них не должно быть особых точек или разрывов, если их нет в реальном процессе, и т. д. Уравнения не должны искажать логику реального процесса.

Модель должна адекватно, т. е. по возможности точно, отражать действительность. Адекватность нужна не вообще, а в рассматриваемом диапазоне.

Расхождения между результатами анализа модели и реальным поведением объекта неизбежны, так как модель - это отражение, а не сам объект.

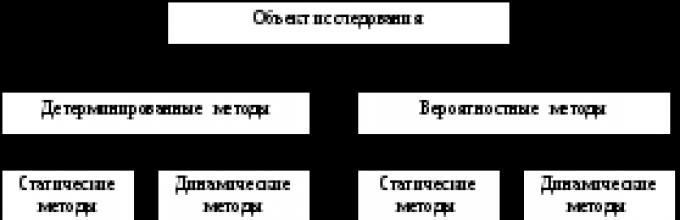
На рис. 3. представлено обобщенное представление, которое используется при построении математических моделей.

Рис. 3. Аппарат для построения математических моделей

При использовании статических методов наиболее часто используется аппарат алгебры и дифференциальные уравнения с независимыми от времени аргументами.

В динамических методах таким же образом используются дифференциальные уравнения; интегральные уравнения; уравнения в частных производных; теория автоматического управления; алгебра.

В вероятностных методах используются: теория вероятностей; теория информации; алгебра; теория случайных процессов; теория Марковских процессов; теория автоматов; дифференциальные уравнения.

Важное место при моделировании занимает вопрос о подобии модели и реального объекта. Количественные соответствия между отдельными сторонами процессов, протекающих в реальном объекте и его модели, характеризуются масштабами.

В целом подобие процессов в объектах и модели характеризуется критериями подобия. Критерий подобия - это безразмерный комплекс параметров, характеризующий данный процесс. При проведении исследований в зависимости от области исследований применяют различные критерии. Например, в гидравлике таким критерием является число Рейнольдса (характеризует текучесть жидкости), в теплотехнике - число Нусссельта (характеризует условия теплоотдачи), в механике - критерий Ньютона и т. д.

Считается, что если подобные критерии для модели и исследуемого объекта равны, то модель является правильной.

К теории подобия примыкает еще один метод теоретического исследования - метод анализа размерностей, который основан на двух положениях:

физические закономерности выражаются только произведениями степеней физических величин, которые могут быть положительными, отрицательными, целыми и дробными; размерности обоих частей равенства, выражающего физическую размерность, должны быть одинаковы.

Сравним методику применения математики в практических исследованиях с методикой других естественных наук. Такие науки, как физика, химия, биология изучают непосредственно сам реальный объект (возможно в уменьшенных масштабах и в лабораторных условиях). Научные результаты, после необходимой проверки, также непосредственно можно применить на практике. Математика же изучает не сами объекты, а их модели. Описание объекта и формулировка проблемы переводятся с обычного языка на «язык математики» (формализуются), в результате чего получается математическая модель. Далее эта модель исследуется как математическая задача. Полученные научные результаты не сразу применяются на практике, так как они сформулированы на математическом языке. Поэтому осуществляется обратный процесс - содержательная интерпретация (на языке исходной проблемы) полученных математических результатов. Только после этого решается вопрос об их применении на практике.

Неотъемлемой частью методики прикладной математики является всесторонний анализ реальной проблемы, предшествующий ее математическому моделированию. В целом системный анализ проблемы, предполагает выполнение следующих этапов:

· гуманитарный (доматематический) анализ проблемы;

· математическое исследование проблемы;

· применение полученных результатов на практике.

Проведение такого системного анализа каждой конкретной проблемы должно осуществляться исследовательской группой, включающей экономистов (как постановщиков проблемы или заказчиков), математиков, юристов, социологов, психологов, экологов и т. д. Причем математики, как основные исследователи, должны участвовать не только в «решении» задачи, но и в ее постановке, а также во внедрении результатов на практике.

Для проведения математических исследований экономической задачи требуется выполнение следующих основных этапов:

1. изучение предметной области и определение цели исследования;

2. формулировка проблемы;

3. сбор данных (статистических, экспертных и прочих);

4. построение математической модели;

5. выбор (или разработка) вычислительного метода и построение алгоритма решения задачи;

6. программирование алгоритма и отладка программы;

7. проверка качества модели на контрольном примере;

8. внедрение результатов на практике.

Этапы 1 -3 относятся к доматематической части исследования. Предметная область должна быть досконально изучена самими экономистами для того, чтобы они, как заказчики, могли четко сформулировать проблему и определить цели перед исследователями. Исследователям должны быть предоставлены все необходимые документальные и статистические данные в исчерпывающем объеме. Математиками производится организация, хранения, анализ и обработка данных, предоставленных им в удобной (электронной) форме заказчиками.

Этапы 4 -7 относятся к математической части исследований. Результатом этого этапа является формулировка исходной проблемы в виде строгой математической задачи. Математическую модель редко можно «подобрать» из числа имеющихся, известных моделей (рис.1.1). Процесс подбора параметров модели таким образом, чтобы она соответствовала изучаемому объекту, называется идентификацией модели . Исходя из характера полученной модели (задачи) и цели исследования выбирают либо известный метод, либо приспосабливают (модифицируют) известный метод, либо разрабатывают новый. После этого составляют алгоритм (порядок решения задачи) и программу для ЭВМ. Полученные с помощью этой программы результаты анализируют: решают тестовые задачи, вводят необходимые изменения и исправления в алгоритм и программу.

Если для «чистой» математики традиционным является однократный выбор математической модели и однократная формулировка допущений в самом начале исследования, то в прикладных работах часто бывает полезно вернуться к модели и внести в нее исправления после того, как первый тур пробных расчетов уже произведен. Более того, часто оказывается плодотворным сопоставление моделей, когда одно и то же явление описывается не одной, а несколькими моделями. Если выводы оказываются (приблизительно) одними и теми же при разных моделях, разных методах исследования - это является свидетельством правильности расчетов, адекватности модели самому объекту, объективности выдаваемых рекомендаций.

Заключительный этап 8 проводится совместными усилиями заказчиков и разработчиков модели.

Результаты математических (как и всяких научных) исследований являются только рекомендацией к использованию на практике. Окончательное решение этого вопроса - применять модель или нет - зависит от заказчика, т. е. от лица ответственного за исход и за последствия, к которым приведет применение рекомендуемых результатов.

Для построения математической модели конкретной экономической задачи (проблемы) рекомендуется выполнение следующей последовательности работ:

1. определение известных и неизвестных величин, а также существующих условий и предпосылок (что дано и что требуется найти?);

2. выявление важнейших факторов проблемы;

3. выявление управляемых и неуправляемых параметров;

4. математическое описание посредством уравнений, неравенств, функций и иных отношений взаимосвязей между элементами модели (параметрами, переменными), исходя из содержания рассматриваемой задачи.

Известные параметры задачи относительно ее математической модели считаются внешними (заданными априори, т. е. до построения модели). В экономической литературе они называются экзогенными переменными . Значение же изначально неизвестных переменных вычисляются в результате исследования модели, поэтому по отношению к модели они считаются внутренними . В экономической литературе они называются эндогенными переменными .

В § 2 под важнейшими понимаются факторы, которые играют существенную роль в самой задаче и которые, так или иначе, влияют на конечный результат. В § 3 управляемыми называются те параметры задачи, которым можно придавать произвольные числовые значения исходя из условий задачи; неуправляемыми считаются те параметры, значение которых зафиксировано и не подлежит изменению.

С точки зрения назначения, можно выделить описательные модели и модели принятия решения . Описательные модели отражают содержание и основные свойства экономических объектов как таковых. С их помощью вычисляются числовые значения экономических факторов и показателей.

Модели принятия решения помогают найти наилучшие варианты плановых показателей или управленческих решений. Среди них наименее сложным являются оптимизационные модели, посредством которых описываются (моделируются) задачи типа планирования, а наиболее сложными - игровые модели, описывающие задачи конфликтного характера с учетом пересечения различных интересов. Эти модели отличаются от описательных тем, что в них имеется возможность выбора значений управляющих параметров (что отсутствует в описательных моделях).

Примеры составления математических моделей

Пример 1.1. Пусть некоторый экономический регион производит несколько видов продуктов исключительно своими силами и только для населения данного региона. Предполагается, что технологический процесс отработан, а спрос населения на эти товары изучен. Надо определить годовой объем выпуска продуктов, с учетом того, что этот объем должен обеспечить как конечное, так и производственное потребление.

Составим математическую модель этой задачи. По условию даны: виды продуктов, спрос на них и технологический процесс; требуется найти объем выпуска каждого вида продукта Обозначим известные величины: - спрос населения на -й продукт ; - количество i-го продукта, необходимое для выпуска единицы -го продукта по данной технологии . Обозначим неизвестные величины: - объем выпуска -го продукта . Совокупность называется вектором спроса, числа - технологическими коэффициентами, а совокупность - вектором выпуска. По условию задачи вектор распределяется на две части: на конечное потребление (вектор ) и на воспроизводство (вектор ). Вычислим ту часть вектора которая идет на воспроизводство. В силу обозначений для производства количества -го товара идет количества -го товара. Тогда сумма показывает ту величину -го товара, которая нужна для всего выпуска . Следовательно, должно выполняться равенство:

Обобщая это рассуждение на все виды продуктов, приходим к искомой модели:

Решая полученную систему линейных уравнений относительно находим требуемый вектор выпуска.

Для того чтобы написать эту модель в более компактной (векторной) форме, введем обозначения:

Квадратная матрица А (размером ) называется технологической матрицей. Очевидно, модель можно записать в виде: или

Получили классическую модель «Затраты-выпуск», автором которой является известный американский экономист В. Леонтьев.

Пример 1.2. Нефтеперерабатывающий завод располагает двумя сортами нефти: сортом в количестве 10 единиц, сортом - 15 единиц. При переработке из нефти получаются два материала: бензин () и мазут (). Имеется три варианта технологического процесса переработки:

I : 1ед.А + 2ед.В дает 3ед.Б + 2ед.М ;

II :2ед.А + 1ед.В дает 1ед.Б + 5ед.М ;

III :2ед.А + 2ед.В дает 1ед.Б + 2ед.М.

Цена бензина - 10 долл. за единицу, мазута - 1 долл. за единицу. Требуется определить наиболее выгодное сочетание технологических процессов переработки имеющегося количества нефти.

Перед моделированием уточним следующие моменты. Из условия задачи следует, что «выгодность» технологического процесса для завода следует понимать в смысле получения максимального дохода от реализации своей готовой продукции (бензина и мазута). В связи с этим понятно, что «выбор (принятие) решения» завода состоит в определении того, какую технологию и сколько раз применить. Очевидно, что таких возможных вариантов достаточно много.

Обозначим неизвестные величины: - количество использования -го технологического процесса . Остальные параметры модели (запасы сортов нефти, цены бензина и мазута) известны .

Тогда одно конкретное решение завода сводится к выбору одного вектора , для которого выручка завода равна долл. Здесь 32 долл. - это доход, полученный от одного применения первого технологического процесса (10 долл. 3ед.Б + 1 долл. 2ед.М = 32 долл.). Аналогичный смысл имеют коэффициенты 15 и 12 для второго и третьего технологических процессов соответственно. Учет запаса нефти приводит к следующим условиям:

для сорта А : ,

для сорта В : ,

где в первом неравенстве коэффициенты 1, 2, 2 - это нормы расхода нефти сорта А для одноразового применения технологических процессов I , II , III соответственно. Коэффициенты второго неравенства имеют аналогичный смысл для нефти сорта В .

Математическая модель в целом имеет вид:

Найти такой вектор , чтобы

максимизировать

при выполнении условий:

,

,

.

Сокращенная форма этой записи имеет вид:

при ограничениях

, (1.4.2)

,

Получили так называемую задачу линейного программирования. Модель (1.4.2.) является примером оптимизационной модели детерминированного типа (с вполне определенными элементами).

Пример 1.3. Инвестору требуется определить наилучший набор из акций, облигаций и других ценных бумаг для приобретения их на некоторую сумму с целью получения определенной прибыли с минимальным риском для себя. Прибыль на каждый доллар, вложенный в ценную бумагу - го вида, характеризуется двумя показателями: ожидаемой прибылью и фактической прибылью. Для инвестора желательно, чтобы ожидаемая прибыль на один доллар вложений была для всего набора ценных бумаг не ниже заданной величины . Заметим, что для правильного моделирования этой задачи от математика требуются определенные базовые знания в области портфельной теории ценных бумаг. Обозначим известные параметры задачи: - число разновидностей ценных бумаг; - фактическая прибыль (случайное число) от -го вида ценной бумаги - ожидаемая прибыль от -го вида ценной бумаги. Обозначим неизвестные величины: - средства, выделенные для приобретения ценных бумаг вида . В силу обозначений вся инвестированная сумма определяется как . Для упрощения модели введем новые величины

Таким образом, - это доля от всех средств, выделяемая для приобретения ценных бумаг вида . Очевидно, что . Из условия задачи видно, что цель инвестора - достижение определенного уровня прибыли с минимальным риском. Содержательно риск - это мера отклонения фактической прибыли от ожидаемой. Поэтому его можно отождествить с ковариацией

прибыли для ценных бумаг вида и вида . Здесь М - обозначение математического ожидания. Математическая модель исходной задачи имеет вид:

(1.4.3)

Получили известную модель Марковица для оптимизации структуры портфеля ценных бумаг. Модель (1.4.3.) является примеров оптимизационной модели стохастического типа (с элементами случайности).

Пример 1.4. На базе торговой организации имеется типов одного из товаров ассортиментного минимума. В магазин должен быть завезен только один из типов данного товара. Требуется выбрать тот тип товара, который целесообразно завести в магазин. Если товар типа будет пользоваться спросом, то магазин от его реализации получит прибыль , если же он не будет пользоваться спросом - убыток .

Математическое исследование благодаря своей универсальности применяется в областях, весьма далеких от математики. Это объясняется тем, что любое положение, правило или закон, записанные на математическом языке, ста- новятся инструментом предсказания (прогнозирования), являющегося важнейшей задачей каждого научного исследования.

Основой традиционной (классической) математики является система аксиом, из которых методом дедукции получают результаты, представляемые в виде лемм, теорем и т.п. Получаемые на их основе аналитические решения в пределе являются точными. В рамках этих методов исследуются вопросы существования решений, их единственности, а также устойчивости и сходимости к абсолютно точным решениям при неограниченном возрастании их числа.

Разработка таких методов способствует развитию собственно математики (появлению новых ее разделов и направлений). Однако для решения многих прикладных задач они оказываются малоэффективными, так как для их использования необходимо вводить массу допущений, приводящих к тому, что математическая модель исследуемого процесса оказывается существенно отличающейся от реального физического процесса.

В связи с этим в математике возникло ответвление, называемое прикладной математикой. Ее основное отличие от традиционной состоит в том, что здесь находится не точное, а приближенное решение с точностью, достаточной для инженерных приложений, но без учета тех допущений, которые принимаются в рамках классической математики. Оценка точности полученных решений выполняется путем сравнения с точными решениями каких-либо тестовых задач либо с результатами экспериментальных исследований.

К методам прикладной математики относятся вариационные (Ритца, Треффтца, Канторовича и др.), ортогональные методы взвешенных невязок (Бубнова-Галеркина, Канторовича), коллокаций, моментов, наименьших квадратов и др.; вариационно-разностные методы (конечных элементов, граничных элементов; спектральный метод и др.)- Все они относятся к группе так называемых прямых методов - это такие приближенные аналитические методы решения задач математической физики, которые сводят решение дифференциальных и интегральных уравнений к решению систем алгебраических линейных уравнений. Коротко остановимся на хронологии развития этих методов и их физической сути.

В 1662 г. французский математик П. Ферма сформулировал закон преломления света на границе двух сред следующим образом: из всех возможных путей движения света от пункта А к пункту В реализуется тот, на котором время движения достигает минимума. Это была одна из первых формулировок вариационного принципа.

В 1696 г. И. Бернулли сформулировал задачу нахождения длины пути (траектории), по которому материальная точка, двигаясь от точки А под действием только силы тяжести, за наименьшее время достигает точки В. Нахождение такой кривой, называемой брахистохроной (кривой наискорейшего спуска), сводится к определению минимума функционала

при граничных условиях у (0) = 0; у{а) = у а, являющихся координатами точек начала и конца движения.

Здесь Т - время наискорейшего спуска; g - ускорение силы тяжести.

Введением функционала (а) было положено начало появлению вариационного исчисления. Подобные функционалы в общем виде записываются следующим образом:

при граничных условиях у(а) = А = const, y(b) = В = const.

Обычно в задачах математической физики находятся экстремумы некоторых функций у = у(х). Значение вариационного исчисления заключается в том, что здесь определяются экстремумы более сложных, чем функции, величин - экстремумы функционалов J =J от функций у(х). В связи с чем открылись возможности исследования новых физических объектов и развития новых математических направлений.

В 1774 г. Л. Эйлер показал, что если функция у(х) доставляет минимум линейному интегралу J = J [у (х), то она должна удовлетворять некоторым дифференциальным уравнениям, названным впоследствии уравнениями Эйлера. Открытие этого факта явилось важным достижением математического моделирования (построения математических моделей). Стало ясно, что одна и та же математическая модель может быть представлена в двух эквивалентных видах: в виде функционала или в виде дифференциального уравнения Эйлера (системы дифференциальных уравнений). В связи с этим замена дифференциального уравнения функционалом получила название обратной задачи вариационного исчисления. Таким образом, решение задачи на экстремум функционала можно рассматривать так же, как и решение соответствующего этому функционалу дифференциального уравнения Эйлера. Следовательно, математическая постановка одной и той же физической задачи может быть представлена либо в виде функционала с соответствующими граничными условиями (экстремум этого функционала доставляет решение физической задачи), либо в виде соответствующего этому функционалу дифференциального уравнения Эйлера с теми же граничными условиями (интегрирование этого уравнения доставляет решение поставленной задачи).

Широкому распространению вариационных методов в прикладных науках способствовало появление в 1908 г. публикации В. Ритца, связанной с методом минимизации функционалов, названным впоследствии методом Ритца. Этот метод считается классическим вариационным методом. Основная его идея заключается в том, что искомая функция у = у(х) у доставляющая функционалу (А) с граничными условиями у (а) = А, у(Ъ ) = В минимальное значение, разыскивается в виде ряда

где Cj (i = 0, гг) - неизвестные коэффициенты; (р/(д) (г = 0, п) - координатные функции (алгебраический или тригонометрический полипом).

Координатные функции находятся в таком виде, чтобы они точно удовлетворяли граничным условиям задачи.

Подставляя (с) в (А), после определения производных от функционалаJ по неизвестным С, (г = 0, гг) относительно последних получается система алгебраических линейных уравнений. После определения коэффициентов С, решение задачи в замкнутом виде находится из (с).

При использовании большого числа членов ряда (с) (п - 5 ? °о) в принципе можно получить решение требуемой точности. Однако, как показыва- ют расчеты конкретных задач, матрица коэффициентов С, (г = 0, п) представляет собой заполненную квадратную матрицу с большим разбросом коэффициентов по абсолютной величине. Такие матрицы близки к вырожденным и, как правило, являются плохо обусловленными. Это связано с тем, что они не удовлетворяют ни одному из условий, при которых матрицы могут быть хорошо обусловленными. Рассмотрим некоторые из этих условий.

• 1. Положительная определенность матрицы (члены, находящиеся на главной диагонали, должны быть положительными и максимальными).
• 2. Ленточный вид матрицы относительно главной диагонали при минимальной ширине ленты (коэффициенты матрицы, находящиеся вне ленты, равны нулю).
• 3. Симметричность матрицы относительно главной диагонали.

В связи с этим при увеличении приближений в методе Ритца число обусловленности матрицы, определяемое отношением ее максимального собственного числа к минимальному, устремляется к бесконечно большой величине. А точность получаемого при этом решения ввиду быстрого накопления ошибок округления при решении больших систем алгебраических линейных уравнений может не улучшаться, а ухудшаться.

Наряду с методом Ритца развивался родственный с ним метод Галерки- на. В 1913 г. И. Г. Бубнов установил, что алгебраические линейные уравнения относительно неизвестных С, (/ = 0, п ) из (с) можно получать, не используя функционал вида (А). Математическая постановка задачи в данном случае включает дифференциальное уравнение с соответствующими граничными условиями. Решение, как и в методе Ритца, принимается в виде (с). Благодаря особой конструкции координатных функций ф,(х) решение (с) точно удовлетворяет граничным условиям задачи. Для определения неизвестных коэффициентов С, (г = 0, п) составляется невязка дифференциального уравнения и требуется ортогональность невязки ко всем координатным функциям ф 7 Сг) (/ = i = 0, п). Определяя получающиеся при этом интегралы, относительно неизвестных коэффициентов С, (г = 0, гг) получаем систему алгебраических линейных уравнений, которая полностью совпадает с системой аналогичных уравнений метода Ритца. Таким образом, при решении одних и тех же задач с использованием одинаковых систем координатных функций методы Ритца и Бубнова - Галеркина приводят к одинаковым результатам.

Несмотря на идентичность получаемых результатов, важным преимуществом метода Бубнова-Галеркина по сравнению с методом Ритца является то, что он не требует построения вариационного аналога (функционала) дифференциального уравнения. Отметим, что подобный аналог не всегда может быть построен. В связи с этим методом Бубнова-Галеркина могут быть решены задачи, для которых классические вариационные методы неприменимы.

Еще одним методом, относящимся к группе вариационных, является метод Канторовича . Его отличительным признаком является то, что в качестве неизвестных коэффициентов в линейных комбинациях вида (с) принимаются не константы, а функции, зависящие от одной из независимых переменных задачи (например, времени). Здесь, как и в методе Бубнова-Галеркина, составляется невязка дифференциального уравнения и требуется ортогональность невязки ко всем координатным функциям (ру(дг) (j = i = 0, п). После определения интегралов относительно неизвестных функций fj(x) будем иметь систему обыкновенных дифференциальных уравнений первого порядка. Методы решения таких систем хорошо разработаны (имеются стандартные программы для ЭВМ).

Одним из направлений при решении краевых задач является совместное использование точных (Фурье, интегральных преобразований и др.) и приближенных (вариационных, взвешенных невязок, коллокаций и др.) аналитических методов. Такой комплексный подход позволяет наилучшим образом использовать положительные стороны этих двух важнейших аппаратов прикладной математики, так как появляется возможность без проведения тонких и громоздких математических расчетов в простой форме получать выражения, эквивалентные главной части точного решения, состоящего из бесконечного функционального ряда. Для практических расчетов, как правило, используется именно эта час- тичная сумма нескольких слагаемых . При использовании таких методов для получения более точных результатов на начальном участке параболической координаты необходимо выполнять большое число приближений. Однако при большом п координатные функции с соседними индексами приводят к алгебраическим уравнениям, связанным почти линейной зависимостью. Матрица коэффициентов в этом случае, являясь заполненной квадратной матрицей, близка к вырожденной и оказывается, как правило, плохо обусловленной. И при п - 3 ? °° приближенное решение может не сходиться даже к слабо точному решению. Решение систем алгебраических линейных уравнений с плохо обусловленными матрицами представляет существенные технические трудности вследствие быстрого накопления ошибок округления. Поэтому такие системы уравнений необходимо решать с большой точностью промежуточных вычислений .

Особое место среди приближенных аналитических методов, позволяющих получать аналитические решения на начальном участке временной (параболической) координаты занимают методы, в которых используется понятие фронта температурного возмущения. Согласно этим методам, весь процесс нагрева или охлаждения тел формально разделяется на две стадии. Первая из них характеризуется постепенным распространением фронта температурного возмущения от поверхности тела к его центру, а вторая - изменением температуры но всему объему тела вплоть до наступления стационарного состояния. Такое разделение теплового процесса по времени на две стадии позволяет осуществлять поэтапное решение задач нестационарной теплопроводности и для каждой из стадий в отдельности, как правило, уже в первом приближении находить удовлетворительные по точности, достаточно простые и удобные в инженерных приложениях расчетные формулы. Данные методы обладают и существенным недостатком, заключающимся в необходимости априорного выбора координатной зависимости искомой температурной функции. Обычно принимаются квадратичная или кубическая параболы. Эта неоднозначность решения порождает проблему точности, так как, принимая заранее тот или иной профиль температурного поля, всякий раз будем получать различные конечные результаты.

Среди методов, в которых используется идея конечной скорости перемещения фронта температурного возмущения, наибольшее распространение получил интегральный метод теплового баланса . С его помощью уравнение в частных производных удается свести к обыкновенному дифференциальному уравнению с заданными начальными условиями, решение которого довольно часто можно получить в замкнутом аналитическом виде. Интегральный метод, например, можно использовать для приближенного решения задач, когда теплофизические свойства не являются постоянными, а определяются сложной функциональной зависимостью, и задач, в которых совместно с теплопроводностью приходится также учитывать и конвекцию. Интегральному методу также присущ отмеченный выше недостаток - априорный выбор температурного профиля, что порождает проблему однозначности решения и приводит к низкой его точности.

Многочисленные примеры применения интегрального метода к решению задач теплопроводности приведены в работе Т. Гудмена . В этой работе наряду с иллюстрацией больших возможностей показана и его ограниченность. Так, несмотря на то что многие задачи успешно решаются интегральным методом, существует целый класс задач, для которых этот метод практически не применим. Это, например, задачи с импульсным изменением входных функций. Причина обусловлена тем, что температурный профиль в виде квадратичной или кубической параболы не соответствует истинному профилю температур для таких задач. Поэтому если истинное распределение температуры в исследуемом теле принимает вид немонотонной функции, то получить удовлетворительное решение, согласующееся с физическим смыслом задачи, ни при каких условиях не удается.

Очевидный путь повышения точности интегрального метода - использование полиномиальных температурных функций более высокого порядка. В этом случае основные граничные условия и условия плавности на фронте температурного возмущения не являются достаточными для определения коэффициентов таких полиномов. В связи с этим возникает необходимость поиска недостающих граничных условий, которые совместно с заданными позволили бы определять коэффициенты оптимального температурного профиля более высокого порядка, учитывающего все физические особенности исследуемой задачи. Такие дополнительные граничные условия могут быть получены из основных граничных условий и исходного дифференциального уравнения их дифференцированием в граничных точках но пространственной координате и но времени .

При исследовании различных задач теплообмена предполагают, что теп- лофизические свойства не зависят от температуры, а в качестве граничных принимают линейные условия. Однако если температура тела изменяется в широких пределах, то ввиду зависимости теплофизических свойств от температуры уравнение теплопроводности становится нелинейным. Его решение значительно усложняется, и известные точные аналитические методы оказываются неэффективными. Интегральный метод теплового баланса позволяет преодолеть некоторые трудности, связанные с нелинейностью задачи. Например, с его помощью уравнение в частных производных с нелинейными граничными условиями приводится к обыкновенному дифференциальному уравнению с заданными начальными условиями, решение которого часто может быть получено в замкнутой аналитической форме.

Известно, что точные аналитические решения в настоящее время получены лишь для задач в упрощенной математической постановке, когда не учитываются многие важные характеристики процессов (нелинейность, переменность свойств и граничных условий и пр.). Все это приводит к существенному отклонению математических моделей от реальных физических процессов, протекающих в конкретных энергетических установках. К тому же точные решения выражаются сложными бесконечными функциональными рядами, которые в окрестностях граничных точек и при малых значениях временной координаты являются медленно сходящимися. Такие решения малопригодны для инженерных приложений, и особенно в случаях, когда решение температурной задачи является промежуточным этапом решения каких-либо других задач (задач термоуиругости, обратных задач, задач управления и др.). В связи с этим большой интерес представляют перечисленные выше методы прикладной математики, позволяющие получать решения, хотя и приближенные, но в аналитической форме, с точностью, во многих случаях достаточной для инженерных приложений. Эти методы позволяют значительно расширить круг задач, для которых могут быть получены аналитические решения по сравнению с классическими методами.