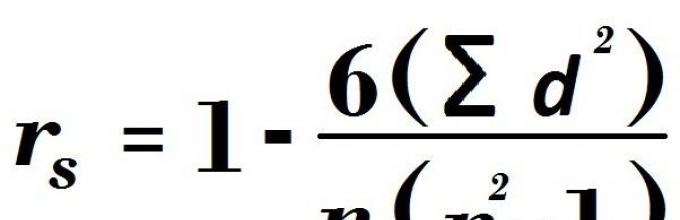Коэффициент корреляции Спирмена. Коэффициент ранговой корреляции Спирмена. Проверка значимости корреляции. Методы корреляционного анализа

Корреляция Пирсона есть мера линейной связи между двумя переменными. Она позволяет определить, насколько пропорциональна изменчивость двух переменных. Если переменные пропорциональны друг другу, то графически связь между ними можно представить в виде прямой линии с положительным (прямая пропорция) или отрицательным (обратная пропорция) наклоном.

На практике связь между двумя переменными, если она есть, является вероятностной и графически выглядит как облако рассеивания эллипсоидной формы. Этот эллипсоид, однако, можно представить (аппроксимировать) в виде прямой линии, или линии регрессии. Линия регрессии - это прямая, построенная методом наименьших квадратов: сумма квадратов расстояний (вычисленных по оси Y) от каждой точки графика рассеивания до прямой является минимальной

Особое значение для оценки точности предсказания имеет дисперсия оценок зависимой переменной. По сути, дисперсия оценок зависимой переменной Y - это та часть ее полной дисперсии, которая обусловлена влиянием независимой переменной X. Иначе говоря, отношение дисперсии оценок зависимой переменной к ее истинной дисперсии равно квадрату коэффициента корреляции.

Квадрат коэффициента корреляции зависимой и независимой переменных представляет долю дисперсии зависимой переменной, обусловленной влиянием независимой переменной, и называется коэффициентом детерминации. Коэффициент детерминации, таким образом, показывает, в какой степени изменчивость одной переменной обусловлена (детерминирована) влиянием другой переменной.

Коэффициент детерминации обладает важным преимуществом по сравнению с коэффициентом корреляции. Корреляция __________не является линейной функцией связи между двумя переменными. Поэтому, среднее арифметическое коэффициентов корреляции для нескольких выборок не совпадает с корреляцией, вычисленной сразу для всех испытуемых из этих выборок (т.е. коэффициент корреляции не аддитивен). Напротив, коэффициент детерминации отражает связь линейно и поэтому является аддитивным: допускается его усреднение для нескольких выборок.

Дополнительную информацию о силе связи дает значение коэффициента корреляции в квадрате - коэффициент детерминации: это часть дисперсии одной переменной, которая может быть объяснена влиянием другой переменной. В отличие от коэффициента корреляции коэффициент детерминации линейно возрастает с увеличением силы связи.

Коэффициенты корреляции Спирмена и τ-Кендалла (ранговые корреляции)

Если обе переменные, между которыми изучается связь, представлены в порядковой шкале, или одна из них - в порядковой, а другая - в метрической, то применяются ранговые коэффициенты корреляции: Спирмена или τ-Кенделла. И тот, и другой коэффициент требует для своего применения предварительного ранжирования обеих переменных.

Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Если члены группы численностью были ранжированы сначала по переменной x, затем – по переменной y, то корреляцию между переменными x и y можно получить, просто вычислив коэффициент Пирсона для двух рядов рангов. При условии отсутствия связей в рангах (т.е. отсутствия повторяющихся рангов) по той и другой переменной, формула для Пирсона может быть существенно упрощена в вычислительном отношении и преобразована в формулу, известную как Спирмена.

Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции.

Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности.

Коэффициент ранговой корреляции Спирмена при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений.

Альтернативу корреляции Спирмена для рангов представляет корреляция τ-Кендалла. В основе корреляции, предложенной М.Кендаллом, лежит идея о том, что о направлении связи можно судить, попарно сравнивая между собой испытуемых: если у пары испытуемых изменение по x совпадает по направлению с изменением по y, то это свидетельствует о положительной связи, если не совпадает - то об отрицательной связи.

Калькулятор ниже вычисляет коэффициент ранговой корреляции Спирмена между двумя случайными величинами. Теоретическая часть, чтобы не отвлекаться от калькулятора, традиционно размещается под ним.

add import_export mode_edit delete

Изменения случайных величин

Изменения случайных величин

Импортировать данные Ошибка импорта

Для разделения полей можно использовать один из этих символов: Tab, ";" или "," Пример: -50.5;-50.5

Импортировать Назад Отменить

Метод расчета коэффициента ранговой корреляции Спирмена на самом деле описывается очень просто. Это тот же самый Коэффициент корреляции Пирсона , только рассчитанный не для самих результатов измерений случайных величин, а для их ранговых значений .

То есть,

Осталось только разобраться, что такое ранговые значения и для чего все это нужно.

Если элементы вариационного ряда расположить в порядке возрастания или убывания, то рангом элемента будет являться его номер в этом упорядоченном ряду.

Например, пусть у нас есть вариационный ряд {17,26,5,14,21}. Отсортируем его элементы в порядке убывания {26,21,17,14,5}. 26 имеет ранг 1, 21 - ранг 2 и т.д. Вариационный ряд ранговых значений будет выглядеть следующим образом {3,1,5,4,2}.

То есть, при расчете коэффициента Спирмена исходные вариационные ряды преобразуются в вариационные ряды ранговых значений, после чего к ним применяется формула Пирсона.

Есть одна тонкость - ранг повторяющихся значений берется как среднее из рангов. То есть для ряда {17, 15, 14, 15} ряд ранговых значений будет выглядеть как {1, 2.5, 4, 2.5}, так как первый элемент равный 15 имеет ранг 2, а второй - ранг 3, и .

Если же повторяющихся значений нет, то есть все значения ранговых рядов - числа из диапазона от 1 до n, формулу Пирсона можно упростить до

Ну и кстати, эта формула чаще всего и приводится как формула расчета коэффицента Спирмена.

В чем же суть перехода от самих значений к их ранговым значениям?
А суть в том, что исследуя корреляцию ранговых значений можно установить насколько хорошо зависимость двух переменных описывается монотонной функцией.

Знак коэффициента указывает на направление связи между переменными. Если знак положительный, то значения Y имеют тенденцию увеличиваться при увеличении значений X; если знак отрицательный, то значения Y имеют тенденцию уменьшаться при увеличении значений X. Если коэффициент равен 0, то никакой тенденции нет. Если же коэффициент равен 1 или -1, то зависимость между X и Y имеет вид монотонной функции - то есть, при увеличении X, Y также увеличивается, либо наоборот, при увеличении X, Y уменьшается.

То есть, в отличие от коэффициента корреляции Пирсона, который может выявить только линейную зависимость одной переменной от другой, коэффициент корреляции Спирмена может выявить монотонную зависимость, там, где непосредственная линейная связь не выявляется.

Поясню на примере. Предположим, что мы исследуем функцию y=10/x.
У нас есть следующие результаты измерений X и Y
{{1,10}, {5,2}, {10,1}, {20,0.5}, {100,0.1}}
Для этих данных коэффициент корреляции Пирсона равен -0.4686, то есть связь слабая либо отсутствует. А вот коэффициент корреляции Спирмена строго равен -1, что как бы намекает исследователю, что Y имеет строгую отрицательную монотонную зависимость от X.

Дисциплина "высшая математика" у некоторых вызывает неприятие, так как поистине не всем дано ее понять. Но те, кому посчастливилось изучать этот предмет и решать задачи, используя различные уравнения и коэффициенты, могут похвастаться практически полной в ней осведемленности. В психологической науке существует не только гуманитарная направленность, но и определенные формулы и способы для математической проверки выдвигаемой в ходе исследований гипотезы. Для этого применяются различные коэффициенты.

Коэффициент корреляции Спирмена

Это распространенное измерение по определению тесноты связи между какими-либо двумя признаками. Коэффициент еще называют непараметрическим методом. Он показывает статистику связи. То есть мы знаем, например, что у ребенка агрессия и раздражительность связаны между собой, а коэффициент корреляции рангов Спирмена показывает статистическую математическую связь этих двух признаков.

Как вычисляется ранговый коэффициент?

Естественно, что для всех математических определений или величин существуют свои формулы, по которым они вычисляются. Ею обладает и коэффициент корреляции Спирмена. Формула у него следующая:

С первого взгляда формула не совсем понятна, но если разобраться, все очень легко вычисляется:

• n - это количество признаков или показателей, которые проранжированы.
• d - разность определенных двух рангов, соответствующих конкретным двум переменным каждого испытуемого.
• ∑d 2 - сумма всех квадратов разностей рангов признака, квадраты которых вычисляются отдельно для каждого ранга.

Область применения математической меры связи

Для применения рангового коэффициента необходимо, чтобы количественные данные признака были проранжированы, то есть им был присвоен определенный номер в зависимости от места, на котором расположен признак, и от его значения. Доказано, что два ряда признаков, выраженных в числовом виде, несколько параллельны между собой. Коэффициент ранговой корреляции Спирмена определяет степень этой параллельности, тесноты связи признаков.

Для математической операции по расчету и определению связи признаков с помощью указанного коэффициента нужно произвести некоторые действия:

1. Каждому значению какого-либо испытуемого или явления присваивается номер по порядку - ранг. Он может соответствовать значению явления по возрастанию и по убыванию.
2. Дальше сопоставляются ранги значения признаков двух количественных рядов для того, чтобы определить разность между ними.
3. В отдельном столбце таблицы для каждой полученной разности прописывается ее квадрат, а внизу результаты суммируются.
4. После этих действий применяется формула, по которой рассчитывается коэффициент корреляции Спирмена.

Свойства коэффициента корреляции

К основным свойствам коэффициента Спирмена относят следующие:

• Измерение значений в пределах от -1 до 1.
• Знак коэффициента интерпретаций не имеет.
• Теснота связи определяется по принципу: чем выше величина, тем теснее связь.

Как проверить полученное значение?

Для проверки связи признаков между собой необходимо выполнить определенные действия:

1. Выдвигается нулевая гипотеза (H0), она же основная, затем формулируется другая, альтернативная первой (H 1). Первая гипотеза будет заключаться в том, что коэффициент корреляции Спирмена равняется 0 - это значит, что связи не будет. Вторая, наоборот, гласит, что коэффициент не равен 0, тогда связь есть.
2. Следующим действием будет нахождение наблюдаемого значения критерия. Оно находится по основной формуле коэффициента Спирмена.
3. Далее находятся критические значения заданного критерия. Это можно сделать только с помощью специальной таблицы, где отображаются различные значения по заданным показателям: уровень значимости (l) и число, определяющее (n).
4. Теперь нужно сравнить два полученных значения: установленного наблюдаемого, а также критического. Для этого необходимо построить критическую область. Нужно начертить прямую линию, на ней отметить точки критического значения коэффициента со знаком "-" и со знаком"+". Слева и справа от критических значений полукругами от точек откладываются критические области. Посередине, объединяя два значения, отмечается полукругом ОПГ.
5. После этого делается вывод о тесноте связи между двумя признаками.

Где лучше использовать эту величину

Самой первой наукой, где активно использовался этот коэффициент, была психология. Ведь это наука, не основывающаяся на цифрах, однако для доказательства каких-либо важных гипотез, касающихся развития отношений, черт характера людей, знаний студентов, требуется статистическое подтверждение выводов. Также его используют в экономике, в частности, при валютных оборотах. Здесь оцениваются признаки без статистики. Очень удобен коэффициент ранговой корреляции Спирмена в этой области применения тем, что оценка производится независимо от распределения переменных, так как они заменяются ранговым числом. Активно применяется коэффициент Спирмена в банковском деле. Социология, политология, демография и другие науки также используют его в своих исследованиях. Результаты получаются быстро и максимально точно.

Удобно и быстро используется коэффициент корреляции Спирмена в Excel. Здесь существуют специальные функции, которые помогают быстро получить необходимые значения.

Какие еще коэффициенты корреляции существуют?

Кроме того, что мы узнали про коэффициент корреляции Спирмена, существуют еще различные корреляционные коэффициенты, позволяющие измерить, оценить качественные признаки, связь между количественными признаками, тесноту связи между ними, представленными в ранговой шкале. Это такие коэффициенты, как биссериальный, рангово-биссериальный, контенгенции, ассоциации, и так далее. Коэффициент Спирмена очень точно показывает тесноту связи, в отличие от всех остальных методов ее математического определения.

В случаях, если измерения исследуемых признаков проводятся в шкале порядка, или же форма взаимосвязи отличается от линейной, исследование взаимосвязи между двумя случайными величинами осуществляется с помощь ранговых коэффициентов корреляции. Рассмотрим коэффициент ранговой корреляции Спирмена. При его вычислении необходимо ранжировать (упорядочить) варианты выборки. Ранжированием называется группировка экспериментальных данных в определенном порядке, либо по возрастанию, либо по убыванию.

Проведение операции ранжирования осуществляется по следующему алгоритму:

1. Меньшему значению начисляется меньший ранг. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений. Наименьшему значению начисляется ранг равный 1. Например, если n=7, то наибольшее значение получит ранг под номером 7, за исключением случаев, которые предусмотрены вторым правилом.

2. Если несколько значений равны, то им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны. В качестве примера рассмотрим упорядоченную по возрастанию выборку, состоящую из 7 элементов: 22, 23, 25, 25, 25, 28, 30. Значения 22 и 23 встречаются по одному разу, поэтому их ранги соответственно равны R22=1, а R23=2. Значение 25 встречается 3 раза. Если бы эти значения не повторялись, то их ранги были бы равными 3, 4, 5. Поэтому их ранг R25 равен среднему арифметическому 3, 4 и 5: . Значения 28 и 30 не повторяются, поэтому их ранги соответственно равны R28=6, а R30=7. Окончательно имеем следующее соответствие:

3. Общая сумма рангов должна совпадать с расчетной, которая определяется по формуле:

где n - общее количество ранжируемых значений.

Несовпадение реальной и расчетной сумм рангов будет свидетельствовать об ошибке, допущенной при начислении рангов или их суммировании. В этом случае необходимо найти и исправить ошибку.

Коэффициент ранговой корреляции Спирмена является методом, позволяющим определить силу и направленность взаимосвязи между двумя признаками или двумя иерархиями признаков. Применение коэффициента ранговой корреляции имеет ряд ограничений:

• а) Предполагаемая корреляционная зависимость должна носить монотонный характер.
• б) Объем каждой из выборок должен быть больше или равен 5. Для определения верхней границы выборки пользуются таблицами критических значений (Таблица 3 Приложения). Максимальное значение n в таблице - 40.
• в) При проведении анализа вероятна возможность возникновения большого количества одинаковых рангов. В этом случае, необходимо вносить поправку. Наиболее благоприятным является случай когда, обе изучаемые выборки представляют собой две последовательности несовпадающих значений.

Для проведения корреляционного анализа исследователь должен располагать двумя выборками, которые могут быть ранжированы, например:

• - два признака, измеренные в одной и той же группе испытуемых;
• - две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков;
• - две групповые иерархии признаков;
• - индивидуальная и групповая иерархии признаков.

Расчет начинаем с ранжирования изучаемых показателей отдельно по каждому из признаков.

Проведем анализ случая с двумя признаками, измеренными в одной и той же группе испытуемых. Сначала ранжируют индивидуальные значения по первому признаку, полученные разными испытуемыми, а затем индивидуальные значения по второму признаку. Если меньшим рангам одного показателя соответствуют меньшие ранги другого показателя, а большим рангам одного показателя соответствуют большие ранги другого показателя, то два признака связаны положительно. Если же большим рангам одного показателя соответствуют меньшие ранги другого показателя, то два признака связаны отрицательно. Для нахождения rs, определяем разности между рангами (d) по каждому испытуемому. Чем меньше разности между рангами, тем ближе коэффициент ранговой корреляции rs будет к «+1». Если взаимосвязь отсутствует, то между ними не будет никакого соответствия, следовательно rs окажется близким к нулю. Чем больше разности между рангами испытуемых по двум переменным, тем ближе к «-1» будет значение коэффициента rs. Таким образом, коэффициент ранговой корреляции Спирмена является мерой любой монотонной зависимости между двумя исследуемыми признаками.

Рассмотрим случай с двумя индивидуальными иерархиями признаков, выявленными у двух испытуемых по одному и тому же набору признаков. В данной ситуации ранжируют индивидуальные значения, полученные каждым из двух испытуемым по определенной совокупности признаков. Признаку с самым низким значением необходимо присвоить первый ранг; признаку с более высоким значением - второй ранг и т.д. Следует обратить особое внимание на то, чтобы все признаки были измерены в одних и тех же единицах. Например, невозможно ранжировать показатели, если они выражены в различных по «цене» баллах, поскольку невозможно определить, какой из факторов будет занимать первое место по выраженности, пока все значения не будут приведены к единой шкале. Если признаки, имеющие низкие ранги у одного из испытуемых так же имеют низкие ранги у другого, и наоборот, то индивидуальные иерархии связаны положительно.

В случае с двумя групповыми иерархиями признаков, ранжируют средне-групповые значения, полученные в двух группах испытуемых по одинаковому для исследуемых групп, набору признаков. Далее следует придерживаемся алгоритма, приведенного в предыдущих случаях.

Проведем анализ случая с индивидуальной и групповой иерархией признаков. Начинают с того, что ранжируют отдельно индивидуальные значения испытуемого и средне-групповые значения по тому же набору признаков, которые получены, при исключении того испытуемого, который не участвует в средне-групповой иерархии, так как с ней будет сопоставляться его индивидуальная иерархия. Ранговая корреляция позволяет оценить степень согласованности индивидуальной и групповой иерархии признаков.

Рассмотрим, как определяется значимость коэффициента корреляции в перечисленных выше случаях. В случае с двумя признаками она будет определяться объемом выборки. В случае с двумя индивидуальными иерархиями признаков значимость зависит от количества признаков, входящих в иерархию. В двух последних случаях значимость обуславливается числом изучаемых признаков, а не численностью групп. Таким образом, значимость rs во всех случаях определяется числом ранжированных значений n.

При проверке статистической значимости rs пользуются таблицами критических значений коэффициента ранговой корреляции, составленных для различных количеств ранжируемых значений и разных уровней значимости. Если абсолютная величина rs, достигает критического значения или превышает его, то корреляция достоверна.

При рассмотрении первого варианта (случай с двумя признаками, измеренными в одной и той же группе испытуемых) возможны следующие гипотезы.

Н0: Корреляция между переменными x и y не отличается от нуля.

Н1: Корреляция между переменными x и y достоверно отличается от нуля.

Если мы работаем с любым из трех оставшихся случаев, то необходимо выдвинуть другую пару гипотез:

Н0: Корреляция между иерархиями x и y не отличается от нуля.

Н1: Корреляция между иерархиями x и y достоверно отличается от нуля.

Последовательность действий при вычислении коэффициента ранговой корреляции Спирмена rs такова.

• - Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные x и y.
• - Ранжировать значения переменной x, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Поместить ранги в первую колонку таблицы по порядку номеров испытуемых или признаков.
• - Ранжировать значения переменной y. Поместить ранги во вторую колонку таблицы по порядку номеров испытуемых или признаков.
• - Вычислить разности d между рангами x и y по каждой строке таблицы. Результаты поместить в следующую колонку таблицы.
• - Вычислить квадраты разностей (d2). Полученные значения поместить в четвертую колонку таблицы.
• - Вычислить сумму квадратов разностей? d2.
• - При возникновении одинаковых рангов вычислить поправки:

где tx - объем каждой группы одинаковых рангов в выборке x;

ty - объем каждой группы одинаковых рангов в выборке y.

Вычислить коэффициент ранговой корреляции в зависимости от наличия или отсутствия одинаковых рангов. При отсутствии одинаковых рангов коэффициент ранговой корреляции rs рассчитать по формуле:

При наличии одинаковых рангов коэффициент ранговой корреляции rs рассчитать по формуле:

где?d2 - сумма квадратов разностей между рангами;

Tx и Ty - поправки на одинаковые ранги;

n - количество испытуемых или признаков, участвовавших в ранжировании.

Определить по таблице 3 Приложения критические значения rs, для данного количества испытуемых n. Достоверное отличие от нуля коэффициента корреляции будет наблюдаться при условии, если rs не меньше критического значения.

Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин.

Величина коэффициента корреляции Спирмена также лежит в интервале +1 и -1. Он, как и коэффициент Пирсона, может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале.

В принципе число ранжируемых признаков (качеств, черт и т.п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков -- затруднителен. Возможно, что именно поэтому таблица критических значений рангового коэффициента корреляции рассчитана лишь для сорока ранжируемых признаков (n < 40, табл. 20 приложения 6).

Ранговый коэффициент корреляции Спирмена подсчитывается по формуле:

где n - количество ранжируемых признаков (показателей, испытуемых);

D - разность между рангами по двум переменным для каждого испытуемого;

Сумма квадратов разностей рангов.

Используя ранговый коэффициент корреляции, рассмотрим следующий пример.

Пример : Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.

Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. Результаты представим в табл. 13.

Таблица 13

Подставляем полученные данные в формулу и производим расчет. Получаем:

Для нахождения уровня значимости обращаемся к табл. 20 приложения 6, в которой приведены критические значения для коэффициентов ранговой корреляции.

Подчеркнем, что в табл. 20 приложения 6, как и в таблице для линейной корреляции Пирсона, все величины коэффициентов корреляции даны по абсолютной величине. Поэтому, знак коэффициента корреляции учитывается только при его интерпретации.

Нахождение уровней значимости в данной таблице осуществляется по числу n, т. е. по числу испытуемых. В нашем случае n = 11. Для этого числа находим :

0,61 для P 0,05

0,76 для P 0,01

Строим соответствующую ``ось значимости"":

Полученный коэффициент корреляции совпал с критическим значением для уровня значимости в 1%. Следовательно, можно утверждать, что показатели школьной готовности и итоговые оценки первоклассников связаны положительной корреляционной зависимостью - иначе говоря, чем выше показатель школьной готовности, тем лучше учится первоклассник. В терминах статистических гипотез психолог должен отклонить нулевую (Нгипотезу о сходстве и принять альтернативную (Но наличии различий, которая говорит о том, что связь между показателями школьной готовности и средней успеваемостью отлична от нуля.

Случай одинаковых (равных) рангов

При наличии одинаковых рангов формула расчета коэффициента линейной корреляции Спирмена будет несколько иной. В этом случае в формулу вычисления коэффициентов корреляции добавляются два новых члена, учитывающие одинаковые ранги. Они называются поправками на одинаковые ранги и добавляются в числитель расчетной формулы.

где n - число одинаковых рангов в первом столбце,

k - число одинаковых рангов во втором столбце.

Если имеется две группы одинаковых рангов, в каком-либо столбце то формула поправки несколько усложняется:

где n - число одинаковых рангов в первой группе ранжируемого столбца,

k - число одинаковых рангов в второй группе ранжируемого столбца. Модификация формулы в общем случае такова:

Пример : Психолог, используя тест умственного развития (ШТУР) проводит исследование интеллекта у 12 учащихся 9 класса. Одновременно с этим, но просит учителей литературы и математики провести ранжирование этих же учащихся по показателям умственного развития. Задача заключается в том, чтобы определить, как связаны между собой объективные показатели умственного развития (данные ШТУРа) и экспертные оценки учителей.

Экспериментальные данные этой задачи и дополнительные столбцы, необходимые для расчета коэффициента корреляции Спирмена, представим в виде табл. 14.

Таблица 14

Поскольку при ранжировании использовались одинаковые ранги, то необходимо проверить правильность ранжирования во втором, третьем и четвертом столбцах таблицы. Суммирование в каждом из этих столбцов дает одинаковую сумму - 78.

Проверяем по расчетной формуле. Проверка дает:

В пятом и шестом столбцах таблицы приведены величины разности рангов между экспертными оценками психолога по тесту ШТУР для каждого ученика и величинами экспертных оценок учителей, соответственно по математике и литературе. Сумма величин разностей рангов должна быть равна нулю. Суммирование величин D в пятом и шестом столбцах дало искомый результат. Следовательно, вычитание рангов проведено правильно. Подобную проверку необходимо делать каждый раз при проведении сложных видов ранжирования.

Прежде, чем начать расчет по формуле необходимо рассчитать поправки на одинаковые ранги для второго, третьего и четвертого столбцов таблицы.

В нашем случае во втором столбце таблицы два одинаковых ранга, следовательно, по формуле величина поправки D1 будет:

В третьем столбце три одинаковых ранга, следовательно, по формуле величина поправки D2 будет:

В четвертом столбце таблицы две группы по три одинаковых ранга, следовательно, по формуле величина поправки D3 будет:

Прежде, чем преступить к решению задачи, напомним, что психолог выясняет два вопроса - как связаны величины рангов по тесту ШТУР с экспертными оценками по математике и литературе. Именно поэтому расчет проводится дважды.

Считаем первый ранговый коэффициент с учетом добавок по формуле. Получаем:

Подсчитаем без учета добавки:

Как видим, разница в величинах коэффициентов корреляции оказалась очень незначительной.

Считаем второй ранговый коэффициент с учетом добавок по формуле. Получаем:

Подсчитаем без учета добавки:

И опять, различия оказались очень незначительны. Поскольку число учащихся в обоих случаях одинаково, по табл. 20 приложения 6 находим критические значения при n = 12 сразу для обоих коэффициентов корреляции.

0,58 для P 0,05

0,73 для P 0,01

Откладываем первое значение на ``оси значимости"":

В первом случае полученный коэффициент ранговой корреляции находится в зоне значимости. Поэтому психолог должен отклонить нулевую Нгипотезу о сходстве коэффициента корреляции с нулем и принять альтернативную Но значимом отличии коэффициента корреляции от нуля. Иными словами, полученный результат говорит о том, что чем выше экспертные оценки учащихся по тесту ШТУР, тем выше их экспертные оценки по математике.

Откладываем второе значение на ``оси значимости"":

Во втором случае коэффициент ранговой корреляции находится в зоне неопределенности. Поэтому психолог может принять нулевую Нгипотезу о сходстве коэффициента корреляции с нулем и отклонить альтернативную Но значимом отличии коэффициента корреляции от нуля. В этом случае полученный результат говорит о том, что экспертные оценки учащихся по тесту ШТУР не связаны с экспертными оценками по литературе.

Для применения коэффициента корреляции Спирмена, необходимо соблюдать следующие условия:

1. Сравниваемые переменные должны быть получены в порядковой (ранговой) шкале, но могут быть измерены также в шкале интервалов и отношений.

2. Характер распределения коррелируемых величин не имеет значения.

3. Число варьирующих признаков в сравниваемых переменных X и Y должно быть одинаковым.

Таблицы для определения критических значений коэффициента корреляции Спирмена (табл. 20 приложение 6) рассчитаны от числа признаков равных n = 5 до n = 40 и при большем числе сравниваемых переменных следует использовать таблицу для пирсоновского коэффициента корреляции (табл. 19 приложение 6). Нахождение критических значений осуществляется при k = n.