Численные методы 1

Решение нелинейных уравнений 1

Постановка задачи 1

Локализация корней 2

Уточнение корней 4

Методы уточнения корней 4

Метод половинного деления 4

Метод хорд 5

Метод Ньютона (метод касательных) 6

Численное интегрирование 7

Постановка задачи 7

Метод прямоугольников 8

Метод трапеций 9

Метод парабол (формула Симпсона) 10

Численные методы

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит потому, что искомое решение обычно не выражается в элементарных или других известных функциях. Поэтому большое значение приобрели численные методы.

Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. В зависимости от сложности задачи, заданной точности, применяемого метода может потребоваться огромное количество действий, и здесь без быстродействующего компьютера не обойтись.

Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения задачи являются:

погрешность метода решения;

погрешности округлений в действиях над числами.

Погрешность метода вызвана тем, что численным методом обычно решается другая, более простая задача, аппроксимирующая (приближающая) исходную задачу. В ряде случаев численный метод представляет собойбесконечный процесс , которыйв пределе приводит к искомому решению. Процесс, прерванный на некотором шаге, дает приближенное решение.

Погрешность округления зависит от количества арифметических действий, выполняемых в процессе решения задачи. Для решения одной и той же задачи могут применяться различные численные методы. Чувствительность к погрешностям округления существенно зависит от выбранного метода.

Решение нелинейных уравнений Постановка задачи

Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих в различных разделах физики, химии, биологии и других областях науки и техники.

В общем случае нелинейное уравнение с одним неизвестным можно записать:

f (x ) = 0 ,

где f (x ) – некоторая непрерывная функция аргументаx .

Всякое число x 0 , при которомf (x 0 ) ≡ 0, называется корнем уравненияf (x ) = 0.

Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) иитерационные . Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени не удается получить аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с любой заданной точностью.

При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на осиx , в пределах которых содержится один единственный корень, иуточнение корней , т.е. вычисление приближенных значений корней с заданной точностью.

Локализация корней

Для отделения корней уравнения f (x ) = 0 необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке [a ,b ] имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке.

Если функция f (x ) непрерывна на отрезке [a ,b ], а на концах отрезка её значения имеют разные знаки, т. е.

f (a )  f (b ) < 0 ,

то на этом отрезке расположен, по крайней мере, один корень.

Рис 1. Отделение корней. Функция f (x ) не монотонна на отрезке [a ,b ].

Это условие, как видно из рисунка (1), не обеспечивает единственности корня. Достаточным дополнительным условием, обеспечивающем единственность корня на отрезке [a ,b ] является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием постоянства знака первой производнойf ′(x ) .

Таким образом, если на отрезке [ a ,b ] функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень.

Воспользовавшись этим критерием, можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически , если удается построить график функцииy =f (x ) . Например, график функции на рисунке (1) показывает, что эта функция на интервале может быть разбита на три интервала монотонности и на этом интервале у нее существуют три корня.

Отделение корней можно также выполнить табличным способом. Допустим, что все интересующие нас корни уравнения (2.1) находятся на отрезке [A, B ]. Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи.

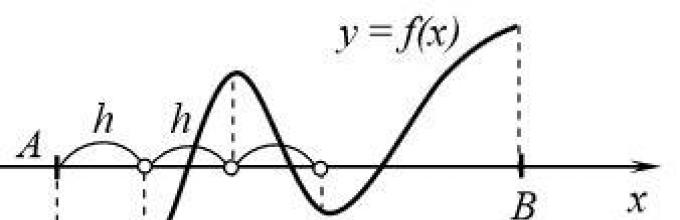
Рис. 2. Табличный способ локализации корней.

Будем вычислять значения f (x ) , начиная с точкиx =A , двигаясь вправо с некоторым шагомh (рис. 2). Как только обнаруживается пара соседних значенийf (x ) , имеющих разные знаки, так соответствующие значения аргументаx можно считать границами отрезка, содержащего корень.

Надежность табличного способа отделения корней уравнений зависит как от характера функции f (x ) , так и от выбранной величины шагаh . Действительно, если при достаточно малом значенииh (h <<|B −A |) на границах текущего отрезка [x, x +h ] функцияf (x ) принимает значения одного знака, то естественно ожидать, что уравнениеf (x ) = 0 корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функцииf (x ) на отрезке [x, x +h ] могут оказаться корни уравнения (рис. 3а).

Рис 3а Рис 3б

Также несколько корней на отрезке [x, x +h ] могут оказаться и при выполнении условияf (x )  f (x + h ) < 0 (рис. 3б). Предвидя подобные ситуации, следует выбирать достаточно малые значенияh .

Отделяя таким образом корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска (h /2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

Назначение сервиса . Сервис предназначен для нахождения корней уравнений f(x) в онлайн режиме методом хорд.

Инструкция . Введите выражение F(x) , нажмите Далее. Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel . Ниже представлена видеоинструкция.

F(x) =

Искать в интервале от до
Точность ξ =
Количество интервалов разбиения , n =
Метод решения нелинейных уравнений Метод дихотомии Метод Ньютона (метод касательных) Модифицированный метод Ньютона Метод хорд Комбинированный метод Метод золотого сечения Метод итераций Метод секущих

Правила ввода функции

Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Рассмотрим более быстрый способ нахождения корня на интервале , в предположении, что f(a)f(b)<0.
f’’(x)>0 f’’(x)<0
f(b)f’’(b)>0 f(a)f’’(a)>0


Рис.1а Рис. 1б

Рассмотрим рис.1а. Проведем через точки А и В хорду. Уравнение хорды
.
В точке x=x 1 , y=0, в результате получим первое приближение корня
. (3.8)
Проверяем условия
(а) f(x 1)f(b)<0,
(б) f(x 1)f(a)<0.
Если выполняется условие (а), то в формуле (3.8) точку a заменяем на x 1 , получим

.

Продолжая этот процесс, получим для n-го приближения
. (3.9)
Здесь подвижен конец a, то есть f(x i)f(b)<0. Аналогичная ситуация на рис 2а.
Рассмотрим случай, когда неподвижен конец a .
f’’(x)<0 f’’(x)>0
f(b)f’’(b)<0 f(a)f’’(a)<0


Рис.2а Рис.2б

На рис 1б,2б выполняется f(x i)f(a)<0. Записав уравнение хорды, мы на первом шаге итерационного процесса получим x 1 (см. (3.8)). Здесь выполняется f(x 1)f(a)<0. Затем вводим b 1 =x 1 (в формуле (3.8) точку b заменяем на x 1), получим
.

Продолжая процесс, придем к формуле
. (3.10)
Останов процесса

|x n – x n-1 |<ε; ξ≈x n

Рис. 3
На рис.3 f’’(x) меняет знак, поэтому подвижными будут оба конца.
Прежде чем перейти к вопросу о сходимости итерационного процесса метода хорд введем понятие выпуклой функции.

Определение. Непрерывная на функция называется выпуклой (вогнутой), если для любых двух точек x 1 ,x 2 , удовлетворяющих a≤x 1 f(αx 1 + (1-α)x 2) ≤ αf(x 1) + (1-α)f(x 2) - выпуклая.
f(αx 1 + (1-α)x 2) ≥ αf(x 1) + (1-α)f(x 2) - вогнутая
Для выпуклой функции f’’(x)≥0.
Для вогнутой функции f’’(x)≤0

Теорема 3. Если функция f(x) выпукла (вогнута) на отрезке , то на любом отрезке график функции f(x) лежит не выше (не ниже) хорды, проходящей через точки графика с абсциссами x 1 и x 2 .

Доказательство:

Рассмотрим выпуклую функцию. Уравнение хорды: проходящей через x 1 и x 2 имеет вид:
.
Рассмотрим точку c= αx 1 + (1-α)x 2 , где aÎ

С другой стороны, по определению выпуклой функции имеем f(αx 1 + (1-α)x 2) ≤ αf 1 + (1-α)f 2 ; поэтому f(c) ≤ g(c) ч.т.д.

Для вогнутой функции доказательство аналогично.
Доказательство сходимости итерационного процесса рассмотрим для случая выпуклой (вогнутой) функции.

Теорема 4. Пусть задана непрерывная: дважды дифференцируемая функция f(x) на и пусть f(a)f(b)<0, а f’(x) и f’’(x) сохраняют свои знаки на (см. рис 1а,1б и рис 2а,2б). Тогда итерационный процесс метода хорд сходится к корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим для примера случай f(a)f’’(a)<0 (см рис 1а и 2а). Из формулы (9) следует, что x n > x n -1 так как (b-x n -1)>0, а f n -1 /(f b -f n -1)<0. Это справедливо для любого n, то есть получаем возрастающую последовательность чисел
a≤x 0 Докажем теперь, что все приближения x n < ξ, где ξ - корень. Пусть x n -1 < ξ. Покажем, что x n тоже меньше ξ. Введем
. (3.11)
Имеем
(3.12)
(то есть значение функции y(x) в точке x n на хорде совпадает с f(ξ)).
Так как , то из (3.12) следует
или
. (3.13)
Для рис. 1а , следовательно
или
значит что и т.д. (см. (3.11)).
Для рис 2а . Следовательно, из (3.12) получим
значит
так как ч.т.д.
Аналогичное доказательство для рис.1б и рис.2б. Таким образом, мы доказали, что последовательность чисел является сходящейся.
a≤x 0 a≤ ξЭто значит, что для любого ε можно указать такое n, что будет выполняться |x n - ξ |<ε. Теорема доказана.
Сходимость метода хорд линейная с коэффициентом .
, (3.14)
где m 1 =min|f’(x)|, M 1 =max|f’(x)|.
Это вытекает из следующих формул. Рассмотрим случай неподвижного конца b и f(b)>0.
Имеем из (3.9) . Отсюда
. Учитывая, что , мы можем записать или
.
Заменяя в знаменателе правой части (ξ-x n -1) на (b-x n -1) и учитывая, что (ξ-x n -1)< (b-x n -1), получим , что и требовалось доказать (см. неравенство (3.14)).
Доказательство сходимости для случая рис.3 (f’’(x) меняет знак; в общем случае как f’, так и f’’ могут менять знаки) более сложное и здесь не приводится.

В задачах определить количество действительных корней уравнения f(x) = 0, отделить эти корни и, применяя метод хорд и касательных, найти их приближенные значения с точностью до 0.001.

Наименование параметра	Значение
Тема статьи:	Метод хорд.
Рубрика (тематическая категория)	Математика

Метод хорд - один из распространенных итерационных методов. Его еще называют методом линœейного интерполирования, методом пропорциональных частей.

Идея метода хорд в том, что на достаточно малом отрезке дуга кривой у =f (x) заменяется хордой и абсцисса точки пересечения хорды с осью Ox является приближенным значением корня.

Рисунок 2 – Геометрическая интерпретация метода Ньютона.

Пусть для определœенности f" (х)> 0, f"" (x) >0, f (а) <0, f (b)> 0 (рис. 3, а). Возьмем за начальное приближение искомого корня х* значения х 0 =а. Через точки а 0 и В проведем хорду и за первое приближение корня х* возьмем абсциссу x 1 точки пересечения хорды с осью ОХ. Теперь приближенное значение х 1 корня можно уточнить если применить метод хорд на отрезке [х 1 ; b ]. Абсцисса х 2 точки пересечения хордыА 1 В будет другим приближением корня. Продолжая данный процесс далее, получим последовательность х 0 , х 1 , х 2 ,..., х k , ... приближенных значений корня х* данного уравнения.

Таким образом метод хорд можно записать так:

, k=0, 1.2, …, (8)

В общем случае неподвижным будет тот конец отрезка изолированного корня, в которой знак функции f(х) совпадает со знаком второй производной, а за начальное приближение x 0 можно взять точку отрезка [а; b ], в которой f(x 0)×f"’(x 0) < 0.

К примеру, когда f (a) >0, f (b) <0, f"(х)< 0, f"(х)< 0 (рис. .3, б) конец b отрезка [а; b ] является неподвижным.

В случае если f (а)>0, f (b)< 0, f" (х)< 0, f"(x) >0 (рис.3, в), или f (а) <0, f (b) >0, f’ (х) >0, f"’ (x) <0 (рис. 3, г), точка а является неподвижным концом отрезка [а; b ].

Достаточные условия сходимости метода хорд дает такая теорема.

Рисунок 3. – Геометрическая интерпретация метода хорд

Теорема. Пусть на отрезке [а; b ] функция f (х) непрерывна вместе со своими производными второго порядка включительно, причем f(a)×f(b)<0, а производные f" (x) и f" (х) сохраняют свои знаки на [а; b ], тогда существует такая окружность корня х* уравнения f (x) =0, что для любого начального приближения х 0 этой окружности последовательность {х k }, вычисленная по формуле (8), сходится к корню х*.

Метод хорд. - понятие и виды. Классификация и особенности категории "Метод хорд." 2017, 2018.

- Метод хорд

Пусть 1) функция y=F(x) определена и непрерывна на отрезке . 2) F(a)F(b)<0 Требуется найти корень на отрезке с точностью &... .

- МЕТОД ХОРД

При дифференцировании этим методом отмечают ряд точек на вычерченной кривой графика функции, которые соединяют хордами, т.е. заменяют заданную кривую ломаной линией (Рис.2). Принимают следующее допущение: угол наклона касательных в точках, расположенных посередине... .

- Метод хорд

В некоторых случаях несколько большей скоростью сходимости обладает метод хорд, у которого на втором этапе при выборе очередного приближения внутри отрезка, содержащего корень, учитывается величина невязки на концах отрезка: точка выбирается ближе к тому концу, где... .

- Метод хорд.

Идея метода проиллюстрирована рисунком. Задается интервал , на котором f(x0)f(x1) &... .

- Метод хорд

В данном методе в качестве приближения выбирается не середина отрезка, а точка пересечения хорды с осью абсцисс. Уравнение хорды АВ, соединяющей концы отрезка: (1) Точка пересечения с осью абсцисс имеет координаты, подставим в (1) и найдем (2). Сравниваем знаки и... .

- Комбинированный метод хорд и касательных

Если и - приближенные значения корня по недостатку и избытку. 1. Если на, то, при этом. 2. Если на, то, при этом. Пример. Отделить корни аналитически и уточнить их комбинированным методом хорд и касательных с точностью до 0,001. , следовательно, для вычислений...

Метод хорд (метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .

В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось - Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.

Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).

Рис.1. Построение отрезка (хорды) к функции .

Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов - умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:

или .

Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

Рис.2. Пояснение к определению погрешности расчета.

Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.

Алгоритм нахождения корня нелинейного уравнения по методу хорд

1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации () .

2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:

Если выполняется условие , то искомый корень находится внутри левого отрезка положить, ;

Если выполняется условие , то искомый корень находится внутри правого отрезка принять , .

В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

Если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

Если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.

Пример решения уравнений методом хорд

В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .

Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд

Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .

Примечание:

Модификацией данного метода является метод ложного положения (False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.

Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:

Случай №1:

Из первого условия получается, что неподвижной стороной отрезка является – сторона a .

Случай №2: