Трапецией называется выпуклый четырёхугольник, у которого параллельны две противоположные стороны и непараллельны две другие. Если все противоположные стороны четырёхугольника попарно параллельны, то это параллелограмм.

Вам понадобится

  • - все стороны трапеции (AB, BC, CD, DA).

Инструкция

  • Непараллельные стороны трапеции называются боковыми сторонами, а параллельные - основаниями. Линия между основаниями, перпендикулярная к ним - высота трапеции . Если боковые стороны трапеции равны, то она называется равнобедренной. Сначала рассмотрим решение для трапеции , которая не является равнобедренной.
  • Проведите отрезок BE из точки B к нижнему основанию AD параллельно боковой стороне трапеции CD. Поскольку BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE - параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
  • Рассмотрите треугольник ABE. Вычислите сторону AE. AE=AD-ED. Основания трапеции BC и AD известны, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
  • Теперь узнайте площадь треугольника ABE по формуле Герона, вычислив полупериметр. S=корень(p*(p-AB)*(p-BE)*(p-AE)). В этой формуле p - полупериметр треугольника ABE. p=1/2*(AB+BE+AE). Для вычисления площади вам известны все необходимые данные: AB, BE=CD, AE=AD-BC.
  • Далее запишите площадь треугольника ABE другим способом - она равна половине произведения высоты треугольника BH и стороны AE, к которой она проведена. S=1/2*BH*AE.
  • Выразите из этой формулы высоту треугольника, которая является и высотой трапеции . BH=2*S/AE. Вычислите её.

    • Если трапеция равнобедренная, решение можно выполнить по-другому. Рассмотрите треугольник ABH. Он прямоугольный, так как один из углов, BHA, прямой.

  • Проведите из вершины C высоту CF.
  • Изучите фигуру HBCF. HBCF прямоугольник, поскольку две его стороны - высоты, а другие две являются основаниями трапеции , то есть углы прямые, а противолежащие стороны параллельны. Это значит, что BC=HF.
  • Посмотрите на прямоугольные треугольники ABH и FCD. Углы при высотах BHA и CFD прямые, а углы при боковых стороных BAH и CDF равны, так как трапеция ABCD равнобедренная, значит, треугольники подобны. Так как высоты BH и CF равны или боковые стороны равнобедренной трапеции AB и CD равны, то и подобные треугольники равны. Значит, их стороны AH и FD тоже равны.
  • Найдите AH. AH+FD=AD-HF. Так как из параллелограмма HF=BC, а из треугольников AH=FD, то AH=(AD-BC)*1/2.
  • Далее из прямоугольного треугольника ABH по теореме Пифагора рассчитайте высоту BH. Квадрат гипотенузы AB равен сумме квадратов катетов AH и BH. BH=корень(AB*AB-AH*AH).

Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:

, где DP – внешняя высота в

Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:

Вынесем за скобку

Что и требовалось доказать.

Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то

2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда

3) Метод сдвига диагонали
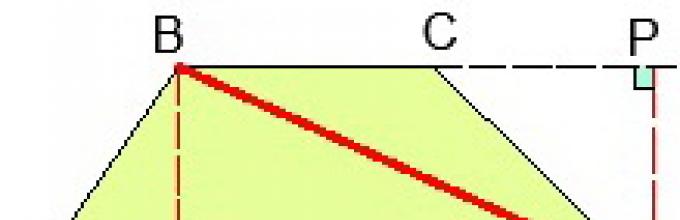
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:

Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).

Спецприемы репетитора по математике.

Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:

Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:

Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.

В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!

Задачи на площадь трапеции:

Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.

1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).

Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.

Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .

Многоликая трапеция... Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.

Несколько слов о трапеции и ее элементах

Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.

Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.

Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.

Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.

Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:

  • высота, то есть отрезок, перпендикулярный обоим основаниям;
  • средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?

Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.

Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:

S = ((а 1 + а 2)/2)*н.

Формула, по которой вычисляется площадь, если даны ее высота и средняя линия

Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:

S = l * н.

Возможность найти площадь по диагоналям

Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:

S = ((д 1 * д 2)/2) * sin α.

В этом выражении можно легко заменить α на β. Результат не изменится.

Как узнать площадь, если известны все стороны фигуры?

Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:

S = ((а 1 + а 2) / 2) * √ {в 1 2 - [(а 1 - а 2) 2 + в 1 2 - в 2 2) / (2 * (а 1 - а 2))] 2 }.

Способы вычисления площади равнобедренной трапеции

Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:

S = (4 * r 2) / sin γ.

Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:

S = ((а 1 + а 2) / 2) * √ {в 2 - [(а 1 - а 2) 2 / (2 * (а 1 - а 2))] 2 }.

Методы вычисления площади прямоугольной трапеции

Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.

Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.

Это достаточно простой способ того, как найти площадь прямоугольной трапеции.

Как быть, если известны координаты вершин трапеции?

В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.

Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.

До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:

длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.

Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.

Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.

Осталось только подставить получавшиеся значения в формулу площади трапеции:

S = ((3 + 9) / 2) * 6 = 36.

Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.

Примеры задач

№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.

Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).

Теперь нужно воспользоваться подходящей формулой для площади:

S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.

Ответ: площадь трапеции равна 4,5 дм 2 .

№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е - середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.

Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.

Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой - накрест лежащий.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.

Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .

Ответ: S = 20 см 2 .

№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание - 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.

Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 - 4) / 2 = 10 / 2 = 5 (см).

Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.

S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).

Ответ: Искомая площадь равна 45 см 2 .

№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.

Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.

Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .

Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:

(х + а 2) * н 1 = 1/5 (х + а 1) * н 2

н 1 /н 2 = (х + а 1) / (5(х + а 2)).

Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:

н 1 /н 2 = (х - а 2) / (а 1 - х).

В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х - а 2) / (а 1 - х).

Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.

Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.


Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:


Следующее важное понятие.

Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?

Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:


*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

Посмотреть ещё одно объяснение

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:


Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.

Теперь рассмотрим треугольник:


*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Площадь трапеции формула:


Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.

То есть, получается, что она равна произведению средней линии и высоты:

Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:


То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:

Но дело тут не в записи, конечно, а в понимании.

Скачать (посмотреть) материал статьи в формате *pdf

На этом всё. Успеха вам!

С уважением, Александр.

В нашей жизни очень часто приходится сталкиваться с применением геометрии на практике, например, в строительстве. Среди наиболее часто встречающихся геометрических фигур есть и трапеция. И для того, чтобы проект был успешным и красивым, необходим правильный и точный расчет элементов для такой фигуры.

Что собой представляет выпуклый четырехугольник, который имеет пару параллельных сторон, именуемых основаниями трапеции. Но есть еще две другие стороны, соединяющие эти основания. Их называют боковыми. Один из вопросов, касающийся данной фигуры, это: «Как найти высоту трапеции?» Сразу необходимо обратить внимание, что высота - это отрезок, определяющий расстояние от одного основания до другого. Существует несколько способов для определения этого расстояния, в зависимости от известных величин.

1. Известны величины обоих оснований, обозначим их b и k, а так же площадь данной трапеции. Используя известные величины, найти высоту трапеции в этом случае очень легко. Как известно из геометрии, вычисляется, как произведение половины суммы оснований и высоты. Из этой формулы можно легко вывести искомую величину. Для этого необходимо площадь разделить на половину суммы оснований. В виде формул это будет выглядеть так:

S=((b+k)/2)*h, отсюда h=S/((b+k)/2)=2*S/(b+k)

2. Известна длина средней линии, обозначим ее d, и площадь. Для тех, кто не знает, средней линией называю расстояние между серединами боковых сторон. Как найти высоту трапеции в этом случае? Согласно свойству трапеции, средняя линия соответствует половине суммы оснований, то есть d=(b+k)/2. Опять же прибегаем к формуле площади. Заменив половину суммы оснований на величину средней линии, получим следующее:

Как видим из полученной формулы очень легко вывести высоту. Разделив площадь на величину средней линии, мы найдем искомую величину. Запишем это формулой:

3. Известна длина одной боковой стороны (b) и угол, образующийся между этой стороной и наибольшим основанием. Ответ на вопрос, как найти высоту трапеции, есть и в этом случае. Рассмотрим трапецию ABCD, где AB и CD являются боковыми сторонами, причем AB=b. Наибольшим основанием является AD. Угол, образованный AB и AD обозначим α. Из точки B опустим высоту h на основание AD. Теперь рассмотрим полученный треугольник ABF, который является прямоугольным. Сторона AB является гипотенузой, а BF-катетом. Из свойства прямоугольного треугольника отношение значения катета и значению гипотенузы соответствует синусу угла, противолежащего катету (BF). Поэтому, исходя из вышеизложенного, для вычисления высоты трапеции перемножаем значение известной стороны и синус угла α. В виде формулы это выглядит следующим образом:

4. Аналогично рассматривается случай, если известны размер боковой стороны и угол, обозначим его β, образующийся между этой стороной и меньшим основанием. При решении такой задачи величина угла между известной боковой стороной и проведенной высотой будет 90°- β. Из свойства треугольников - отношение длины катета и гипотенузы соответствует косинусу угла, расположенного между ними. Из этой формулы легко вывести величину высоты:

h = b *cos(β-90°)

5. Как найти высоту трапеции, если известен лишь радиус вписанной окружности? Из определения окружности, она касается одной точкой каждого основания. Кроме того, эти точки находятся на одной линии с центром окружности. Из этого следует, что расстояние между ними является диаметром и, в то же время, высотой трапеции. Выглядит так:

6. Часто встречаются задачи, в которых необходимо найти высоту равнобедренной трапеции. Напомним, что трапеция, имеющая равные боковые стороны, называется равнобедренной. Как найти высоту равнобедренной трапеции? При перпендикулярных диагоналях высота равна половине суммы оснований.

Но, что делать, если диагонали не перпендикулярны? Рассмотрим равнобедренную трапецию ABCD. Согласно ее свойствам, основания параллельны. Из этого следует, что углы при основаниях также будут равны. Проведем две высоты BF и CM. Исходя из вышесказанного, можно утверждать, что треугольники ABF и DCM равны, то есть AF= DM = (AD - BC)/2 = (b-k)/ 2. Теперь, исходя из условия задачи, определимся с известными величинами, а уж потом находим высоту, учитывая все свойства равнобедренной трапеции.