№1 Дата05.09.14
Предмет Геометрия
Класс 11
Тема урока: Понятие о многогранном угле. Трехгранный угол.
Цели урока:
ввести понятия: “трехгранные углы”, “многогранные углы”, “многогранник”;
ознакомить учащихся с элементами трехгранного и многогранного углов, многогранника, а также определениями выпуклого многогранного угла и свойствами плоских углов многогранного угла;
продолжить работу по развитию пространственных представлений и пространственного воображения, а также логического мышления учащихся.
Тип урока: изучения нового материала
ХОД УРОКА
1. Организационный момент.
Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.
2. Формирование новых понятий и способов действия.
Задачи: Обеспечить восприятие, осмысление и запоминание учащимися изучаемого материала. Обеспечить усвоение учащимися методики воспроизведения изученного материала, содействовать философскому осмыслению усваиваемых понятий, законов, правил, формул. Установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления, провести коррекцию. Обеспечить соотнесение учащимися своего субъективного опыта с признаками научного знания.
Пусть даны три луча а, b и с с общим началом точкой О (рис. 1.1). Эти три луча не обязательно лежат в одной плоскости. На рисунке 1.2 лучи b и с лежат в плоскости р, а луч а не лежит в этой плоскости.
Лучи а, b и с попарно задают три выделенных дугами плоских угла (рис. 1.3).
Рассмотрим фигуру, состоящую из трех указанных выше углов и части пространства, ограниченной этими плоскими углами. Эту пространственную фигуру называют
трехгранным углом
(рис. 2).

Лучи а, b и с называются ребрами трехгранного угла, а углы: = AOC, = AOB,
=
BOC
,
ограничивающие трехгранный угол, - его
гранями.
Эти углы-грани образуют
поверхность трехгранного угла.
Точка
О
называется
вершиной трехгранного угла.
Трехгранный угол можно обозначать так:
OABC

Рассмотрев внимательно все многогранные углы, изображенные на рисунке 3, мы можем заключить, что у каждого из многогранных углов одинаковое число ребер и граней:

4 грани и одна вершина;
у шестигранного угла - 6 ребер, 6 граней и одна вершина и т. д.
у пятигранного угла - 5 ребер, 5 граней и одна вершина;
Многогранные углы бывают выпуклыми и невыпуклыми.
Представьте себе, что мы взяли четыре луча с общим началом, как на рисунке 4. В этом случае мы получили невыпуклый многогранный угол.
Определение 1. Многогранный угол называется выпуклым, если он лежит по одну сторону от плоскости каждой его грани.
Другими словами, выпуклый многогранный угол всегда можно положить любой его гранью на некоторую плоскость. Вы видите, что в случае, изображенном на рисунке 4, так поступить не всегда удается. Четырехгранный угол, изображенный на рисунке 4, является невыпуклым.
Отметим, что в нашем учебнике, если мы говорим “многогранный угол”, то имеем в виду, что он выпуклый. Если рассматриваемый многогранный угол невыпуклый, об этом будет сказано отдельно.
Свойства плоских углов многогранного угла
Теорема 1. Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Теорема 2. Сумма величин всех плоских углов выпуклого многогранного угла меньше 360°.
3. Применение. Формирование умений и навыков.
Задачи: Обеспечить применение учащимися знаний и способов действий, которые им необходимы для СР, создать условия для выявления школьниками индивидуальных способов применения изученного.
6.Этап информации о домашнем задании.
Задачи: Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.
§1(1.1, 1.2) стр. 4, № 9.
7.Подведение итогов урока.
Задача: Дать качественную оценку работы класса и отдельных учащихся.
8.Этап рефлексии.
Задачи: Инициировать рефлексию учащихся на самооценку своей деятельности. Обеспечить усвоение учащимися принципов само регуляции и сотрудничества.
Беседа по вопросам:
Что тебе на уроке было интересно?
Что не понятно?
На что обратить внимание учителю на следующем уроке?
Как ты оценишь свою работу на уроке?
Определения. Возьмём несколько углов (черт. 37): ASB, BSC, CSD, которые, примыкая последовательно один к другому, расположены в одной плоскости вокруг общей вершины S.
Повернём плоскость угла ASВ вокруг общей стороны SB так, чтобы эта плоскость составила некоторый двугранный угол с плоскостью BSC. Затем, не изменяя получившегося двугранного угла, повернём его вокруг прямой SC так, чтобы плоскость BSC составила некоторый двугранный угол с плоскостью CSD. Продолжим такое последовательное вращение вокруг каждой общей стороны. Если при этом последняя сторона SF совместится с первой стороной SA, то образуется фигура (черт. 38), которая называется многогранным углом . Углы ASB, BSC,... называются плоскими углами или гранями , стороны их SA, SB, ... называются рeбрами , а общая вершина S- вершиной многогранного угла.

Каждое ребро является вместе с тем ребром некоторого двугранного угла; поэтому в многогранном угле столько двугранных углов и столько плоских, сколько в нём всех рёбер. Наименьшее число граней в многогранном угле - три; такой угол называется трёхгранным . Могут быть углы четырёхгранные, пятигранные и т. д.
Многогранный угол обозначается или одной буквой S, поставленной у вершины, или же рядом букв SABCDE, из которых первая обозначает вершину, а прочие - рёбра по порядку их расположения.
Многогранный угол называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней, неограниченно продолженной. Таков, например, угол, изображённый на чертеже 38. Наоборот, угол на чертеже 39 нельзя назвать выпуклым, так как он расположен по обе стороны от грани ASB или от грани BSС.

Если все грани многогранного угла пересечём плоскостью, то в сечении образуется многоугольник (abcde ). В выпуклом многогранном угле этот многоугольник тоже выпуклый.
Мы будем рассматривать только выпуклые многогранные углы.
Теорема. В трёхгранном угле каждый плоский угол меньше суммы двух других плоских углов.
Пусть в трёхгранном угле SABC (черт. 40) наибольший из плоских углов есть угол ASC.

Отложим на этом угле угол ASD, равный углу ASB, и проведём какую-нибудь прямую АС, пересекающую SD в некоторой точке D. Отложим SB = SD. Соединив В с А и С, получим \(\Delta\)АВС, в котором
AD + DC < АВ + ВС.
Треугольники ASD и ASB равны, так как они содержат по равному углу, заключённому между равными сторонами: следовательно, AD = AB. Поэтому, если в выведенном неравенстве отбросить равные слагаемые AD и АВ, получим, что DC < ВС.
Теперь замечаем, что у треугольников SCD и SCB две стороны одного равны двум сторонам другого, а третьи стороны не равны; в таком случае против большей из этих сторон лежит больший угол; значит,
∠ CSD < ∠ CSВ.
Прибавив к левой части этого неравенства угол ASD, а к правой равный ему угол ASB, получим то неравенство, которое требовалось доказать:
∠ ASC < ∠ CSB + ∠ ASB.
Мы доказали, что даже наибольший плоский угол меньше суммы двух других углов. Значит, теорема доказана.
Следствие. Отнимем от обеих частей последнего неравенства по углу ASB или по углу CSB; получим:
∠ ASC - ∠ ASB < ∠ CSB;
∠ ASC - ∠CSB < ∠ ASB.
Рассматривая эти неравенства справа налево и приняв во внимание, что угол ASC как наибольший из трёх углов больше разности двух других углов, мы приходим к заключению, что в трёхгранном угле каждый плоский угол больше разности двух других углов .
Теорема. В выпуклом многогранном угле сумма всех плоских углов меньше 4d (360°) .
Пересечём грани (черт. 41) выпуклого угла SABCDE какой-нибудь плоскостью; от этого в сечении получим выпуклый n -угольник ABCDE.

Применяя теорему, доказанную ранее, к каждому из трёхгранных углов, вершины которых находятся в точках А, В, С, D и Е, пахолим:
∠ABC < ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.
Сложим почленно все эти неравенства. Тогда в левой части получим сумму всех углов многоугольника ABCDE, которая равна 2dn - 4d , а в правой - сумму углов треугольников ABS, SBC и т. д., кроме тех углов, которые лежат при вершине S. Обозначив сумму этих последних углов буквой х , мы получим после сложения:
2dn - 4d < 2dn - х .
Так как в разностях 2dn - 4d и 2dn - х уменьшаемые одинаковы, то, чтобы первая разность была меньше второй, необходимо, чтобы вычитаемое 4d было больше вычитаемого х ; значит, 4d > х , т. е. х < 4d .
Простейшие случаи равенства трёхгранных углов
Теоремы. Трёхгранные углы равны, если они имеют:
1) по равному двугранному углу, заключённому между двумя соответственно равными и одинаково расположенными плоскими углами , или
2) по равному плоскому углу, заключённому между двумя соответственно равными и одинаково расположенными двугранными углами .
1) Пусть S и S 1 - два трехгранных угла (черт. 42), у которых ∠ASB = ∠A 1 S 1 B 1 , ∠ASC = ∠A 1 S 1 C 1 (и эти равные углы одинаково расположены) и двугранный угол AS равен двугранному углу A 1 S 1 .

Вложим угол S 1 в угол S так, чтобы у них совпали точки S 1 и S, прямые S 1 A 1 и SA и плоскости A 1 S 1 B 1 и ASB. Тогда ребро S 1 B 1 пойдет по SB (в силу равенства углов A 1 S 1 B 1 и ASB), плоскость A 1 S 1 C 1 пойдёт по ASC (по равенству двугранных углов) и ребро S 1 C 1 пойдёт по ребру SC (в силу равенства углов A 1 S 1 C 1 и ASC). Таким образом, трёхгранные углы совместятся всеми своими рёбрами, т.е. они будут равны.
2) Второй признак, подобно первому, доказывается вложением.
Симметричные многогранные углы
Как известно, вертикальные углы равны, если речь идёт об углах, образованных прямыми или плоскостями. Посмотрим, справедливо ли это утверждение применительно к углам многогранным.

Продолжим (черт. 43) все рёбра угла SABCDE за вершину S, тогда образуется другой многогранный угол SA 1 B 1 C 1 D 1 E 1 , который можно назвать вертикальным по отношению к первому углу. Нетрудно видеть, что у обоих углов равны соответственно и плоские углы, и двугранные, но те и другие расположены в обратном порядке. Действительно, если мы вообразим наблюдателя, который смотрит извне многогранного угла на его вершину, то рёбра SА, SВ, SС, SD, SЕ будут казаться ему расположенными в направлении против движения часовой стрелки, тогда как, смотря на угол SA 1 B 1 C 1 D 1 E 1 , он видит рёбра SА 1 , SВ 1 , ..., расположенными по движению часовой стрелки.
Многогранные углы с соответственно равными плоскими и двугранными углами, но расположенными в обратном порядке вообще не могут совместиться при вложении; значит, они не равны. Такие углы называются симметричными (относительно вершины S). Подробнее о симметрии фигур в пространстве будет сказано ниже.
Другие материалы Многогранные углы Многогранный угол является пространственным аналогом многоугольника на плоскости. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной этой плоскости и ограниченной ею внутренней областью.
Многогранные углы Многогранный угол является пространственным аналогом многоугольника на плоскости. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной этой плоскости и ограниченной ею внутренней областью.
 Определение многогранного угла Поверхность, образованную конечным набором плоских углов A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 с общей вершиной S, в которых соседние углы не имеют общий точек, кроме точек общего луча, а не соседние углы не имеют общих точек, кроме общей вершины, будем называть многогранной поверхностью. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA 1, …, SAn называются ребрами многогранного угла, а сами плоские углы A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 – гранями многогранного угла. Многогранный угол обозначается буквами SA 1…An, указывающими вершину и точки на его ребрах.
Определение многогранного угла Поверхность, образованную конечным набором плоских углов A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 с общей вершиной S, в которых соседние углы не имеют общий точек, кроме точек общего луча, а не соседние углы не имеют общих точек, кроме общей вершины, будем называть многогранной поверхностью. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA 1, …, SAn называются ребрами многогранного угла, а сами плоские углы A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 – гранями многогранного угла. Многогранный угол обозначается буквами SA 1…An, указывающими вершину и точки на его ребрах.
 Виды многогранных углов В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.
Виды многогранных углов В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.
 Упражнение 1 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные углы; б) четырехгранные углы; в) пятигранные углы. Ответ: а) Тетраэдр, куб, додекаэдр; б) октаэдр; в) икосаэдр.
Упражнение 1 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные углы; б) четырехгранные углы; в) пятигранные углы. Ответ: а) Тетраэдр, куб, додекаэдр; б) октаэдр; в) икосаэдр.
 Упражнение 2 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные и четырехгранные углы; б) трехгранные и пятигранные углы; в) четырехгранные и пятигранные углы. Ответ: а) четырехугольная пирамида, треугольная бипирамида; б) пятиугольная пирамида; в) пятиугольная бипирамида.
Упражнение 2 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные и четырехгранные углы; б) трехгранные и пятигранные углы; в) четырехгранные и пятигранные углы. Ответ: а) четырехугольная пирамида, треугольная бипирамида; б) пятиугольная пирамида; в) пятиугольная бипирамида.
 Неравенство треугольника Для треугольника имеет место следующая теорема. Теорема (Неравенство треугольника). Каждая сторона треугольника меньше суммы двух других сторон. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов.
Неравенство треугольника Для треугольника имеет место следующая теорема. Теорема (Неравенство треугольника). Каждая сторона треугольника меньше суммы двух других сторон. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов.
 Доказательство Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства ASB ASC
Доказательство Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства ASB ASC
 Точка пересечения биссектрис Для треугольника имеет место следующая теорема. Теорема. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Биссектральные плоскости двугранных углов трехгранного угла пересекаются по одной прямой.
Точка пересечения биссектрис Для треугольника имеет место следующая теорема. Теорема. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Биссектральные плоскости двугранных углов трехгранного угла пересекаются по одной прямой.
 Доказательство Рассмотрим трехгранный угол SABC. Биссектральная плоскость SAD двугранного угла SA является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SAC. Аналогично, биссектральная плоскость SBE двугранного угла SB является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SBC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех граней трехгранного угла. Следовательно, через нее будет проходить биссектральная плоскость двугранного угла SC.
Доказательство Рассмотрим трехгранный угол SABC. Биссектральная плоскость SAD двугранного угла SA является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SAC. Аналогично, биссектральная плоскость SBE двугранного угла SB является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SBC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех граней трехгранного угла. Следовательно, через нее будет проходить биссектральная плоскость двугранного угла SC.
 Точка пересечения серединных перпендикуляров Для треугольника имеет место следующая теорема. Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через биссектрисы граней трехгранного угла и перпендикулярные этим граням, пересекаются по одной прямой.
Точка пересечения серединных перпендикуляров Для треугольника имеет место следующая теорема. Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через биссектрисы граней трехгранного угла и перпендикулярные этим граням, пересекаются по одной прямой.
 Доказательство Рассмотрим трехгранный угол SABC. Плоскость, проходящая через биссектрису SD угла BSC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SB и SC трехгранного угла SABC. Аналогично, плоскость, проходящая через биссектрису SE угла ASC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SA и SC трехгранного угла SABC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех ребер трехгранного угла. Следовательно, ее будет содержать плоскость, проходящая через биссектрису угла ASB и перпендикулярная его плоскости.
Доказательство Рассмотрим трехгранный угол SABC. Плоскость, проходящая через биссектрису SD угла BSC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SB и SC трехгранного угла SABC. Аналогично, плоскость, проходящая через биссектрису SE угла ASC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SA и SC трехгранного угла SABC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех ребер трехгранного угла. Следовательно, ее будет содержать плоскость, проходящая через биссектрису угла ASB и перпендикулярная его плоскости.
 Точка пересечения медиан Для треугольника имеет место следующая теорема. Теорема. Медианы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и биссектрисы противоположных граней, пересекаются по одной прямой.
Точка пересечения медиан Для треугольника имеет место следующая теорема. Теорема. Медианы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и биссектрисы противоположных граней, пересекаются по одной прямой.
 Доказательство Рассмотрим трехгранный угол SABC. На его ребрах отложим равные отрезки SA = SB = CS. Биссектрисы SD, SE, SF плоских углов трехгранного угла являются медианами треугольников соответственно SBC, SAB. Следовательно, AD, BE, CF – медианы треугольника ABC. Пусть O – точка пересечения медиан. Тогда прямая SO будет линией пересечения рассматриваемых плоскостей.
Доказательство Рассмотрим трехгранный угол SABC. На его ребрах отложим равные отрезки SA = SB = CS. Биссектрисы SD, SE, SF плоских углов трехгранного угла являются медианами треугольников соответственно SBC, SAB. Следовательно, AD, BE, CF – медианы треугольника ABC. Пусть O – точка пересечения медиан. Тогда прямая SO будет линией пересечения рассматриваемых плоскостей.
 Точка пересечения высот Для треугольника имеет место следующая теорема. Теорема. Высоты треугольника или их продолжения пересекаются в одной точке. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и перпендикулярные плоскостям противоположных граней, пересекаются по одной прямой.
Точка пересечения высот Для треугольника имеет место следующая теорема. Теорема. Высоты треугольника или их продолжения пересекаются в одной точке. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и перпендикулярные плоскостям противоположных граней, пересекаются по одной прямой.
 Доказательство Рассмотрим трехгранный угол Sabc. Пусть d, e, f – линии пересечения плоскостей граней трехгранного угла с плоскостями, проходящими через ребра a, b, c этого угла и перпендикулярные соответствующим плоскостям граней. Выберем какую-нибудь точку C на ребре с. Опустим из нее перпендикуляры CD и CE на прямые d и e соответственно. Обозначим A и B точки пересечения прямых CD и CE с прямыми SB и SA соответственно. Прямая d является ортогональной проекцией прямой AD на плоскость BSC. Так как BC перпендикулярна прямой d, то она перпендикулярна и прямой AD. Аналогично, прямая AC перпендикулярна прямой BE. Пусть O – точка пересечения прямых AD и BE. Прямая BC перпендикулярна плоскости SAD, следовательно, она перпендикулярна прямой SO. Аналогично, Прямая AC перпендикулярна плоскости SBE, следовательно, она перпендикулярна прямой SO. Таким образом, прямая SO перпендикулярна прямым BC и AC, следовательно, перпендикулярна плоскости ABC, значит, перпендикулярна и прямой AB. С другой стороны, прямая CO перпендикулярна прямой AB. Таким образом, прямая AB перпендикулярна плоскости SOC. Плоскость SAB проходит через прямую AB, перпендикулярную плоскости SOC, следовательно, сама перпендикулярна этой плоскости. Значит, все три рассматриваемые плоскости пересекаются по прямой SO.
Доказательство Рассмотрим трехгранный угол Sabc. Пусть d, e, f – линии пересечения плоскостей граней трехгранного угла с плоскостями, проходящими через ребра a, b, c этого угла и перпендикулярные соответствующим плоскостям граней. Выберем какую-нибудь точку C на ребре с. Опустим из нее перпендикуляры CD и CE на прямые d и e соответственно. Обозначим A и B точки пересечения прямых CD и CE с прямыми SB и SA соответственно. Прямая d является ортогональной проекцией прямой AD на плоскость BSC. Так как BC перпендикулярна прямой d, то она перпендикулярна и прямой AD. Аналогично, прямая AC перпендикулярна прямой BE. Пусть O – точка пересечения прямых AD и BE. Прямая BC перпендикулярна плоскости SAD, следовательно, она перпендикулярна прямой SO. Аналогично, Прямая AC перпендикулярна плоскости SBE, следовательно, она перпендикулярна прямой SO. Таким образом, прямая SO перпендикулярна прямым BC и AC, следовательно, перпендикулярна плоскости ABC, значит, перпендикулярна и прямой AB. С другой стороны, прямая CO перпендикулярна прямой AB. Таким образом, прямая AB перпендикулярна плоскости SOC. Плоскость SAB проходит через прямую AB, перпендикулярную плоскости SOC, следовательно, сама перпендикулярна этой плоскости. Значит, все три рассматриваемые плоскости пересекаются по прямой SO.
 Сумма плоских углов Теорема. Сумма плоских углов трехгранного угла меньше 360°. Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу неравенства треугольника, имеет место неравенство BAС
Сумма плоских углов Теорема. Сумма плоских углов трехгранного угла меньше 360°. Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу неравенства треугольника, имеет место неравенство BAС
 Выпуклые многогранные углы Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов. Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°. Доказательство аналогично доказательству соответствующего свойства для трехгранного угла.
Выпуклые многогранные углы Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов. Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°. Доказательство аналогично доказательству соответствующего свойства для трехгранного угла. Упражнение 5 Два плоских угла трехгранного угла равны 70° и 80°. В каких границах находится третий плоский угол? Ответ: 10 о
Упражнение 5 Два плоских угла трехгранного угла равны 70° и 80°. В каких границах находится третий плоский угол? Ответ: 10 о
 Упражнение 6 Плоские углы трехгранного угла равны 45°, 45° и 60°. Найдите величину угла между плоскостями плоских углов в 45°. Ответ: 90 о.
Упражнение 6 Плоские углы трехгранного угла равны 45°, 45° и 60°. Найдите величину угла между плоскостями плоских углов в 45°. Ответ: 90 о.
 Упражнение 7 В трехгранном угле два плоских угла равны по 45°; двугранный угол между ними прямой. Найдите третий плоский угол. Ответ: 60 о.
Упражнение 7 В трехгранном угле два плоских угла равны по 45°; двугранный угол между ними прямой. Найдите третий плоский угол. Ответ: 60 о.
 Упражнение 8 Плоские углы трехгранного угла равны 60°, 60° и 90°. На его ребрах от вершины отложены равные отрезки OA, OB, OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC. Ответ: 90 о.
Упражнение 8 Плоские углы трехгранного угла равны 60°, 60° и 90°. На его ребрах от вершины отложены равные отрезки OA, OB, OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC. Ответ: 90 о.
 Упражнение 9 Каждый плоский угол трехгранного угла равен 60°. На одном из его ребер отложен от вершины отрезок, равный 3 см, и из его конца опущен перпендикуляр на противоположную грань. Найдите длину этого перпендикуляра. Ответ: см.
Упражнение 9 Каждый плоский угол трехгранного угла равен 60°. На одном из его ребер отложен от вершины отрезок, равный 3 см, и из его конца опущен перпендикуляр на противоположную грань. Найдите длину этого перпендикуляра. Ответ: см.
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
В планиметрии одним из объектов изучения является угол.
Угол - это геометрическая фигура, состоящая из точки - вершины угла и двух лучей, исходящих из этой точки.
Два угла одна сторона, которых общая и две другие являются продолжением одна другой, в планиметрии называются смежными.
Циркуль можно рассматривать как модель плоского угла.
Вспомним понятие двухгранного угла.
Это фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости в геометрии называется двугранным углом. Полуплоскости - это грани двугранного угла. Прямая а - это ребро двугранного угла.
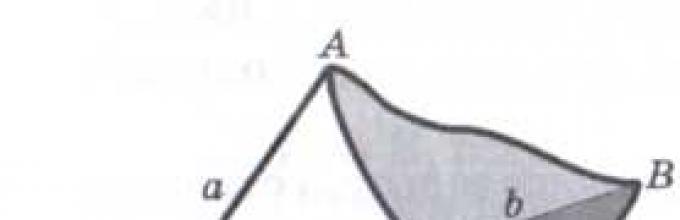
Крыша дома наглядно демонстрирует двухгранный угол.
Но крыша дома на рисунке два выполнена в виде фигуры образованной из шести плоских углов с общей вершиной так, что углы берутся в определенном порядке и каждая пара соседних углов, включая первый и последний, имеет общую сторону. Как называется такая форма крыши?
В геометрии фигура, составленная из углов
А углы из которых составлен этот угол называются плоскими углами. Стороны плоских углов называются ребрами многогранного угла. Точка О называется вершиной угла.

Примеры многогранных углов можно найти в тетраэдре и параллелепипеде.
Грани тетраэдра DBA, ABC, DBC образуют многогранный угол ВADC. Чаще он называется трёхгранным углом.
В параллелепипеде грани АА1D1D, ABCD, AA1B1B образую трехгранный угол AA1DB.
Ну а крыша дома выполнена в форме шестигранного угла. Она состоит из шести плоских углов.
Для многогранного угла справедлив ряд свойств. Сформулируем их и докажем. Здесь говорится, что утверждение

Во-первых, для любого выпуклого многогранного угла существует плоскость, пересекающая все его рёбра.
Рассмотри для доказательства многогранный угол ОА1А2 А3…Аn.
По условию он выпуклый. Угол называется выпуклым, если он лежит по одну сторону от плоскости каждого из своих плоских углов.
Так как по условию этот угол выпуклый, то точки О, А1, А2 ,А3, Аn лежат по одну сторону от плоскости ОА1А2
Проведем среднюю линию KM треугольника ОА1А2 и выберем из ребер ОА3, ОА4, ОАn то ребро которое образует с плоскостью ОКМ, наименьший двугранный угол. Пусть это будет ребро ОАi.(оа итое)
Рассмотрим полуплоскость α с границей КМ, делящую двугранный угол ОКМАi на два двухгранных угла. Все вершины от А до Аn лежат по одну сторону от плоскости α, а точка О по другую сторону. Следовательно, плоскость α пересекает все ребра многогранного угла. Утверждение доказано.
Выпуклые многогранные углы обладают ещё одним важным свойством.
Сумма плоских углов выпуклого многогранного угла меньше 360°.

Рассмотрим выпуклый многогранный угол с вершиной в точке О. В силу доказанного утверждения существует плоскость, которая пересекает все его ребра.
Проведем такую плоскость α, пусть она пересекает рёбра угла в точках А1, А2, А3 и так далее Аn.
Плоскость α от внешней области плоского угла будет отсекать треугольник. Сумма углов которого 180°. Получим, что сумма всех плоских углов от А1ОА2 до АnОА1 равна выражению преобразуем, данное выражение перегруппируем слагаемые, получим
В данном выражении суммы указанные в скобках, являются суммами плоских углов трехгранного угла, а как известно они больше третьего плоского угла.
Данное неравенство можно записать для всех трёхгранных углов образующих данный многогранный угол.
Следовательно, получим следующее продолжение равенства
Полученный ответ доказывает, что сумма плоских углов выпуклого многогранного угла меньше 360 градусов.
20. Разноуровневое изучение многогранных углов, свойств плоских углов трехгранного угла и многогранного угла.
Базовый уровень:
Атанасян
Рассматривает только Двугранный угол.
Погорелов
Сначала рассматривает двугранный угол и затем сразу трехгранный и многогранный.
Рассмотрим три луча а, b, с, исходящие из одной точки лежащие в одной плоскости. Трехгранным углом (abc) называется фигура, составленная из трех плоских углов (ab), (bc) и (ac) (рис. 400). Эти углы называются гранями трехгранного угла, а их стороны - ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Аналогично вводится понятие многогранного угла(рис.401).
рис 400 и рис.401
П рофильный
уровень
(А.Д.Алексндров, А.Л.Вернер,
В.И.Рыжих):
рофильный
уровень
(А.Д.Алексндров, А.Л.Вернер,
В.И.Рыжих):
Оставляя определение и изучение произвольных многогранных углов до § 31, мы рассмотрим сейчас простейшие из них - трехгранные углы. Если в стереометрии аналогами плоских углов можно считать двугранные углы, то трехгранные углы можно рассматривать как аналоги плоских треугольников , а в следующих параграфах увидим, как они естественно связаны со сферическими треугольниками.
Построить (а значит, и конструктивно определить) трехгранный угол можно так. Возьмем любые три луча а, b,c, имеющие общее начало О и не лежащие в одной плоскости (рис. 150). Эти лучи являются сторонами трех выпуклых плоских углов: угла α со сторонамиb, с, угла β со сторонами а, с и угла γ со сторонами а,b. Объединение этих трех углов α, β, γ и называется трехгранным углом Оabc(или, короче, трехгранным углом О). Лучи а,b, с называются ребрами трехгранного угла Оаbс, а плоские углы α, β, γ - его гранями. Точка О называется вершиной трехгранного угла.
3 а м е ч а н и е. Можно было бы определить
трехгранный угол и с невыпуклой гранью
(рис. 151), но мы такие трехгранные углы
рассматривать не будем. 
При каждом из ребер трехгранного угла определяется соответствующий двугранный угол, такой, ребро которого содержит соответствующее ребро трехгранного угла, а грани которого содержат прилежащие к этому ребру грани трехгранного угла.
Величины двугранных углов трехгранного угла Оаbс при ребрах а,b, с будем соответственно обозначать через а^,b^, с^(крышечки непосредственно над буквами).
Три грани α, β, γ трехгранного угла Оаbс и три его двугранных угла при ребрах а,b, с, а также велbчины α, β, γ и а^,b^, с^ будем называть элементами трехгранного угла. (Вспомните, что элементы плоского треугольника - это его стороны и его углы.)
Наша задача - Выразить одни элементы трехгранного угла через другие его элементы, т. е. построить «тригонометрию» трехгранных углов.
1) Начнем с вывода аналога теоремы косинусов. Сначала рассмотрим такой трехгранный угол Оаbс, у которого хотя бы две грани, например α и β являются острыми углами. Возьмем на его ребре с точку С и проведем из нее в гранях α и β перпендикуляры СВ и СА к ребру с до пересечения с ребрами а иbв точках А и В (рис. 152). Выразим расстояние АВ из треугольников ОАВ и САВ по теореме косинусов.
АВ 2 =АС 2 +ВС 2 -2АС*ВС*Cos(c^) и АВ 2 =ОА 2 +ОВ 2 -2АО*ВО*Cosγ.
Вычитая из второго равенства первое, получим:
ОА 2 -АС 2 +ОВ 2 -ВС 2 +2АС*ВС*Cos(c^)-2АО*ВО*Cosγ=0 (1). Т.к. треугольники ОСВ и ОСА прямоугольные, то АС 2 -АС 2 =ОС 2 и ОВ 2 -ВС 2 =ОС 2 (2)
Поэтому из (1) и (2) следует, что ОА*ОВ*Cosγ=ОС 2 +АС*ВС*Cos(c^)
т.е.

Но
 ,
, ,
, ,
, .
Поэтому
.
Поэтому
(3) – аналог теоремы косинусов для трехгранных углов-формула косинусов .
Обе грани α и β – тупые углы.
Один из углов α и β, например α, острый, а другой – β- тупой.
Хоты бы 1 из углов α или β прямой.
Признаки равенства трехгранных углов похожи на признаки равенства треугольников. Но есть отличие: например, два трехгранных угла равны, если соответственно равны их двугранные углы. Вспомните, что два плоских треугольника, у которых соответственные углы равны, подобны. А для трехгранных углов аналогичное условие приводит не к подобию, а к равенству.
Трехгранные углы обладают замечательным свойством , которое называется двойственностью. Если в какой-либо теореме о трехгранном угле Оаbс заменить величины а,b, с на π-α, π-β, π-γи, наоборот, заменить α, β, γ на π-a^, π-b^, π-c^, то снова получим верное утверждение о трехгранных углах, двойственное исходной теореме. Правда, если такую замену произвести в теореме синусов, то снова придем к теореме синусов (она сама себе двойственна). Но если так сделать в теореме косинусов (3), то получим новую формулу
cosc^= -cosa^ cosb^+sina^ sin b^ cosγ.
Почему имеет место такая двойственность, станет ясно, если для трехгранного угла построить двойственный ему трехгранный угол, ребра которого перпендикулярны граням исходного угла (см. п. 33.3 и рис. 356).
Одними из простейших поверхностей являются многогранные углы . Они составляются из обычных углов (такие углы теперь часто будем называть плоскими углами), подобно тому как замкнутая ломаная составляется из отрезков. А именно дается следующее определение:
Многогранным углом называется фигура, образованная плоскими углами так, что выполнены условия:
1) Никакие два угла не имеют общих точек, кроме их общей вершины или целой стороны.
2) У каждого из этих углов каждая его сторона является общей с одним и только с одним другим таким углом.
3) От каждого угла к каждому можно перейти по углам, имеющим общие стороны.
4) Никакие два угла с общей стороной не лежат в одной плоскости (рис. 324).
При этом условии плоские углы, образующие многогранный угол, называются его гранями, а их стороны - его ребра.
Под данное определение подходит и двугранный угол. Он составлен из двух развернутых плоских углов. Вершиной его может считаться любая точка на его ребре, и эта точка разбивает ребро на два ребра, сходящиеся в вершине. Но ввиду этой неопределенности в положении вершины двугранный угол исключают из числа многогранных углов.
П
 онятие
о многогранном угле важно, в частности,
при изучении многогранников - в теории
многогранников. Строение многогранника
характеризуется тем, из каких граней
он составлен и как они сходятся в
вершинах, т. е. какие там оказываются
многогранные углы.
онятие
о многогранном угле важно, в частности,
при изучении многогранников - в теории
многогранников. Строение многогранника
характеризуется тем, из каких граней
он составлен и как они сходятся в
вершинах, т. е. какие там оказываются
многогранные углы.
Рассмотрите многогранные углы у разных многогранников.
Обратите внимание, что грани многогранных углов могут быть и невыпуклыми углами.