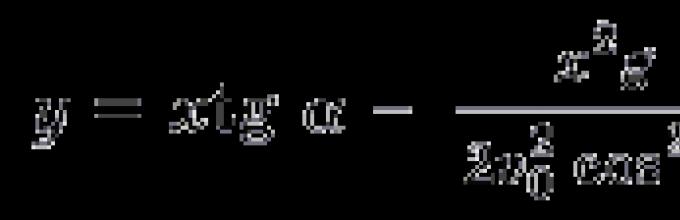Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.

Огромный толчок развитию математического моделирования дало появление ЭВМ, хотя сам метод зародился одновременно с математикой тысячи лет назад. моделирование нелинейный задача математический

Математическое моделирование не всегда требует компьютерной поддержки. Каждый специалист, профессионально занимающийся математическим моделированием, делает все возможное для аналитического исследования модели. Аналитические решения (т. е. представленные формулами, выражающими результаты исследования через исходные данные) обычно удобнее и информативнее численных. Однако возможности аналитических методов решения сложных математических задач очень ограничены и, как правило, эти методы гораздо сложнее численных.

Этапы математического моделирования

С появлением ЭВМ метод математического моделирования занял ведущее место среди других методов исследования. Особенно важную роль этот метод играет в современной экономической науке. Изучение и прогнозирование какого-либо экономического явления методом математического моделирования позволяет проектировать новые технические средства, прогнозировать воздействие на данное явление тех или иных факторов, планировать эти явления даже при существовании нестабильной экономической ситуации.

Построение математической модели - это центральный этап исследования или проектирования любой системы. От качества модели зависит весь последующий анализ объекта. Построение модели - это процедура не формальная. Сильно зависит от исследователя, его опыта и вкуса, всегда опирается на определенный опытный материал. Модель должна быть достаточно точной, адекватной и должна быть удобна для использования.

Основные этапы моделирования

1. Постановка задачи.

Определение цели анализа и пути ее достижения и выработки общего подхода к исследуемой проблеме. На этом этапе требуется глубокое понимание существа поставленной задачи. Иногда, правильно поставить задачу не менее сложно чем ее решить. Постановка - процесс не формальный, общих правил нет.

2. Изучение теоретических основ и сбор информации об объекте оригинала.

На этом этапе подбирается или разрабатывается подходящая теория. Если ее нет, устанавливаются причинно - следственные связи между переменными описывающими объект. Определяются входные и выходные данные, принимаются упрощающие предположения.

В целях правильного построения числовой модели, получения приемлемого оптимального решения особое внимание необходимо уделять подготовке исходной информации, её переработке в технико-экономические характеристики объекта исследования.

Информация как совокупность необходимых для моделирования сведений об процессе и объекте должна быть репрезентативной, содержательной, достаточной, доступной, актуальной, своевременной, точной, достоверной, устойчивой.

На рисунке показана информация, используемая для экономико-математического моделирования. Она разделена на входную, выходную, первичную, вторичную, определенную, стохастическую, неопределенную и другую.

Входную информацию по способу ее использования подразделяют на две основные группы - условно-постоянную (справочную) и переменную.

Условно-постоянная информация объединяет большую группу зафиксированной информации, используемой неоднократно. Информация данной группы используется в моделях в виде нормативных коэффициентов, например, нормы затрат i - го вида производственных ресурсов по j - м видам деятельности, нормы выхода i - го вида продукции по j - м видам деятельности.

Переменная информация обеспечивает разработку и решение конкретной математической задачи. К переменной информации относят многие коэффициенты, сформулированные для данной числовой модели с учетом конкретных условий; задания на гарантированные объемы производства (); главным образом, информацию технико-экономического планирования, оперативных планов производственных процессов, использования средств, финансовые планы и т. п.

Переменная информация используется при моделировании, как правило, одноразово, а затем она теряет свои качества и становится непригодной для дальнейших работ.

По стадии обработки можно выделить первичную и вторичную информацию.

Первая из них возникает непосредственно в процессе деятельности объекта и регистрируется на начальной стадии, а вторичная - является результатом обработки первичной информации и может использоваться в качестве исходных данных для последующих расчетов, либо для выработки управленческих решений.

По продолжительности данные, используемые при моделировании, анализируются в разрезе одного месяца, года или ряда лет.

Информацию можно группировать по уровню обобщения: данные об отраслях, хозяйствах, группах хозяйств, муниципальных образованиях и о регионе.

По степени определенности выделяют производственно-экономическую информацию в виде определенных, стохастических и неопределенных величин.

Определенные (детерминированные) показатели производственных процессов, как правило, являются постоянными и предсказуемыми. К таким показателям относятся земельные ресурсы, площади сельскохозяйственных угодий, сельскохозяйственная техника и другие.

К стохастическим (случайным) величинам относятся такие характеристики, которые могут быть описаны с помощью вероятностных законов распределения. Во многих случаях ряды урожайностей сельскохозяйственных культур в отдельных хозяйствах подчинены гамма и логарифмически нормальному закону распределения. Для хозяйств с неустойчивым сельскохозяйственным производством в группу случайных величин могут попасть затраты, прибыль, трудовые ресурсы.

Под неопределенностью следует понимать отсутствие, неполноту, недостаточность информации об объекте, процессе, явлении или неуверенность в достоверности информации. В ряде случаев сведения о неопределенных характеристиках можно получить с помощью экспертных оценок.

Источниками информации для разработки оптимизационной модели служат годовые отчеты, производственно-финансовые и перспективные планы, данные первичного учета сельскохозяйственных предприятий, технологические карты по возделыванию и уборке сельскохозяйственных культур и выращиванию животных, а также различные нормативные справочники.

3. Формализация.

Заключается в выборе системы условных обозначений и с их помощью записывать отношения между составляющими объекта в виде математических выражений. Устанавливается класс задач, к которым может быть отнесена полученная математическая модель объекта. Значения некоторых параметров на этом этапе еще могут быть не конкретизированы.

4. Выбор метода решения.

На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта. Для полученной математической задачи выбирается какой- либо метод решения или разрабатывается специальный метод. При выборе метода учитываются знания пользователя, его предпочтения, а также предпочтения разработчика.

5. Реализация модели.

Разработав алгоритм, пишется программа, которая отлаживается, тестируется и получается решение нужной задачи.

6. Анализ полученной информации.

Сопоставляется полученное и предполагаемое решение, проводится контроль погрешности моделирования.

7. Проверка адекватности реальному объекту.

Результаты, полученные по модели сопоставляются либо с имеющейся об объекте информацией или проводится эксперимент и его результаты сопоставляются с расчётными.

Процесс моделирования является итеративным. В случае неудовлетворительных результатов этапов 6. или 7. осуществляется возврат к одному из ранних этапов, который мог привести к разработке неудачной модели. Этот этап и все последующие уточняются и такое уточнение модели происходит до тех пор, пока не будут получены приемлемые результаты.

Лекция 1.

МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ

    Современное состояние проблемы моделирования систем

Понятия модели и моделирования

Моделирование можно рассматривать как замещение исследуемогообъекта (оригинала) его условным образом, описанием или другим объектом,именуемым моделью и обеспечивающим близкое к оригиналу поведениев рамках некоторых допущений и приемлемых погрешностей. Моделированиеобычно выполняется с целью познания свойств оригинала путем исследованияего модели, а не самого объекта. Разумеется, моделирование оправдано в томслучае когда оно проще создания самого оригинала или когда последний покаким-то причинам лучше вообще не создавать.

Под моделью понимается физический или абстрактный объект, свойствакоторого в определенном смысле сходны со свойствами исследуемого объекта.При этом требования к модели определяются решаемой задачей и имеющимисясредствами. Существует ряд общих требований к моделям:

2) полнота – предоставление получателю всей необходимой информации

об объекте;

3) гибкость – возможность воспроизведения различных ситуаций во всем

диапазоне изменения условий и параметров;

4) трудоемкость разработки должна быть приемлемой для имеющегося

времени и программных средств.

Моделирование – это процесс построения модели объекта и исследованияего свойств путем исследования модели.

Таким образом, моделирование предполагает 2 основных этапа:

1) разработка модели;

2) исследование модели и получение выводов.

При этом на каждом из этапов решаются разные задачи и используются

отличающиеся по сути методы и средства.

На практике применяют различные методы моделирования. В зависимостиот способа реализации, все модели можно разделить на два больших класса:физические и математические.

Математическое моделирование принято рассматривать как средствоисследования процессов или явлений с помощью их математических моделей.

Под физическим моделированием понимается исследование объектов иявлений на физических моделях, когда изучаемый процесс воспроизводятс сохранением его физической природы или используют другое физическоеявление, аналогичное изучаемому. При этом физические модели предполагают, как правило, реальное воплощение тех физических свойстворигинала, которые являются существенными в конкретной ситуации.Например, при проектировании нового самолета создается его макет,обладающий теми же аэродинамическими свойствами; при планированиизастройки архитекторы изготавливают макет, отражающий пространственноерасположение ее элементов. В связи с этим физическое моделированиеназывают также макетированием .

Полунатурное моделирование представляет собой исследованиеуправляемых систем на моделирующих комплексах с включением в составмодели реальной аппаратуры. Наряду с реальной аппаратурой в замкнутуюмодель входят имитаторы воздействий и помех, математические моделивнешней среды и процессов, для которых неизвестно достаточно точноематематическое описание. Включение реальной аппаратуры или реальныхсистем в контур моделирования сложных процессов позволяет уменьшитьаприорную неопределенность и исследовать процессы, для которых нет точногоматематического описания. С помощью полунатурного моделированияисследования выполняются с учетом малых постоянных времени инелинейностей, присущих реальной аппаратуре. При исследовании моделей свключением реальной аппаратуры используется понятие динамическогомоделирования , при исследовании сложных систем и явлений -эволюционного , имитационного и кибернетического моделирования .

Очевидно, действительная польза от моделирования может быть полученатолько при соблюдении двух условий:

1) модель обеспечивает корректное (адекватное) отображение свойств

оригинала, существенных с точки зрения исследуемой операции;

2) модель позволяет устранить перечисленные выше проблемы, присущие

проведению исследований на реальных объектах.

2. Основные понятия математического моделирования

Решение практических задач математическими методами последовательноосуществляется путем формулировки задачи (разработки математическоймодели), выбора метода исследования полученной математической модели,анализа полученного математического результата. Математическаяформулировка задачи обычно представляется в виде геометрических образов,функций, систем уравнений и т.п. Описание объекта (явления) может бытьпредставлено с помощью непрерывной или дискретной, детерминированнойили стохастической и другими математическими формами.

Теория математического моделирования обеспечивает выявлениезакономерностей протекания различных явлений окружающего мира илиработы систем и устройств путем их математического описания имоделирования без проведения натурных испытаний. При этом используютсяположения и законы математики, описывающие моделируемые явления,системы или устройства на некотором уровне их идеализации.

Математическая модель (ММ) представляет собой формализованноеописание системы (или операции) на некотором абстрактном языке, например,в виде совокупности математических соотношений или схемы алгоритма,т. е. такое математическое описание, которое обеспечивает имитацию работысистем или устройств на уровне, достаточно близком к их реальномуповедению, получаемому при натурных испытаниях систем или устройств.

Любая ММ описывает реальный объект, явление или процесс с некоторойстепенью приближения к действительности. Вид ММ зависит как от природыреального объекта, так и от задач исследования.

Математическое моделирование общественных, экономических,биологических и физических явлений, объектов, систем и различных устройствявляется одним из важнейших средств познания природы и проектированиясамых разнообразных систем и устройств. Известны примеры эффективногоиспользования моделирования в создании ядерных технологий, авиационных иаэрокосмических систем, в прогнозе атмосферных и океанических явлений,погоды и т.д.

Однако для таких серьезных сфер моделирования нередко нужнысуперкомпьютеры и годы работы крупных коллективов ученых по подготовкеданных для моделирования и его отладки. Тем не менее, и в этом случаематематическое моделирование сложных систем и устройств не толькоэкономит средства на проведение исследований и испытаний, но и можетустранить экологические катастрофы – например, позволяет отказаться отиспытаний ядерного и термоядерного оружия в пользу его математическогомоделирования или испытаний аэрокосмических систем перед их реальнымиполетами.Между тем математическое моделирование на уровне решения болеепростых задач, например, из области механики, электротехники, электроники,радиотехники и многих других областей науки и техники в настоящее времястало доступным выполнять на современных ПК. А при использованииобобщенных моделей становится возможным моделирование и достаточносложных систем, например, телекоммуникационных систем и сетей,радиолокационных или радионавигационных комплексов.

Целью математического моделирования является анализ реальныхпроцессов (в природе или технике) математическими методами. В своюочередь, это требует формализации ММ процесса, подлежащего исследованию.Модель может представлять собой математическое выражение, содержащеепеременные, поведение которых аналогично поведению реальной системы.Модель может включать элементы случайности, учитывающие вероятностивозможных действий двух или большего числа «игроков», как, например, втеории игр; либо она может представлять реальные переменные параметрывзаимосвязанных частей действующей системы.

Математическое моделирование для исследования характеристик системможно разделить на аналитическое, имитационное и комбинированное. В своюочередь, ММ делятся на имитационные и аналитические.

Аналитическое моделирование

Для аналитического моделирования характерно, что процессыфункционирования системы записываются в виде некоторых функциональныхсоотношений (алгебраических, дифференциальных, интегральных уравнений). Аналитическая модель может быть исследована следующими методами:

1) аналитическим, когда стремятся получить в общем виде явныезависимости для характеристик систем;

2) численным, когда не удается найти решение уравнений в общем виде иих решают для конкретных начальных данных;

3) качественным, когда при отсутствии решения находят некоторые егосвойства.

Аналитические модели удается получить только для сравнительно простыхсистем. Для сложных систем часто возникают большие математическиепроблемы. Для применения аналитического метода идут на существенноеупрощение первоначальной модели. Однако исследование на упрощенноймодели помогает получить лишь ориентировочные результаты. Аналитическиемодели математически верно отражают связь между входными и выходнымипеременными и параметрами. Но их структура не отражает внутреннююструктуру объекта.

При аналитическом моделировании его результаты представляются в видеаналитических выражений. Например, подключив RC -цепь к источникупостоянного напряжения E (R , C и E - компоненты данной модели), мыможем составить аналитическое выражение для временной зависимостинапряжения u (t ) на конденсаторе C :

Это линейное дифференциальное уравнение (ДУ) и являетсяаналитической моделью данной простой линейной цепи. Его аналитическоерешение, при начальном условии u (0) = 0 , означающем разряженныйконденсатор C в момент начала моделирования, позволяет найти искомуюзависимость – в виде формулы:

u (t ) = E (1− eх p (- t / RC )). (2)

Однако даже в этом простейшем примере требуются определенные усилиядля решения ДУ (1) или для применения систем компьютерной математики (СКМ) с символьными вычислениями – систем компьютернойалгебры. Для данного вполне тривиального случая решение задачимоделирования линейной RC -цепи дает аналитическое выражение (2)достаточно общего вида – оно пригодно для описания работы цепи при любыхноминалах компонентов R , C и E , и описывает экспоненциальный зарядконденсатора C через резистор R от источника постоянного напряжения E .

Безусловно, нахождение аналитических решений при аналитическоммоделировании оказывается исключительно ценным для выявления общихтеоретических закономерностей простых линейных цепей, систем и устройств.Однако его сложность резко возрастает по мере усложнения воздействий намодель и увеличения порядка и числа уравнений состояния, описывающихмоделируемый объект. Можно получить более или менее обозримыерезультаты при моделировании объектов второго или третьего порядка, но ужепри большем порядке аналитические выражения становятся чрезмерногромоздкими, сложными и трудно осмысляемыми. Например, даже простойэлектронный усилитель зачастую содержит десятки компонентов. Тем неменее, многие современные СКМ, например, системы символьной математикиMaple, Mathematica или среда MATLAB , способны в значительноймере автоматизировать решение сложных задач аналитическогомоделирования.

Одной из разновидностей моделирования является численное моделирование, которое заключается в получении необходимыхколичественных данных о поведении систем или устройств каким-либоподходящим численным методом, таким как методы Эйлера илиРунге-Кутта. На практике моделирование нелинейных систем и устройствс использованием численных методов оказывается намного болееэффективным, чем аналитическое моделирование отдельных частных линейныхцепей, систем или устройств. Например, для решения ДУ (1) или систем ДУв более сложных случаях решение в аналитическом виде не получается, но поданным численного моделирования можно получить достаточно полныеданные о поведении моделируемых систем и устройств, а также построитьграфики описывающих это поведение зависимостей.

Имитационное моделирование

Приимитационном 10имоделировании реализующий модель алгоритмвоспроизводит процесс функционирования системы во времени. Имитируютсяэлементарные явления, составляющие процесс, с сохранением их логическойструктуры и последовательности протекания во времени.

Основным преимуществом имитационных моделей по сравнениюсаналитическими является возможность решения более сложных задач.

Имитационные модели позволяют легко учитывать наличие дискретных илинепрерывных элементов, нелинейные характеристики, случайные воздействияи др. Поэтому этот метод широко применяется на этапе проектированиясложных систем. Основным средством реализации имитационногомоделирования служит ЭВМ, позволяющая осуществлять цифровоемоделирование систем и сигналов.

В связи с этим определим словосочетание «компьютерноемоделирование », которое все чаще используется в литературе. Будем полагать,что компьютерное моделирование - это математическое моделированиес использованием средств вычислительной техники. Соответственно,технология компьютерного моделирования предполагает выполнениеследующих действий:

1) определение цели моделирования;

2) разработка концептуальной модели;

3) формализация модели;

4) программная реализация модели;

5) планирование модельных экспериментов;

6) реализация плана эксперимента;

7) анализ и интерпретация результатов моделирования.

При имитационном моделировании используемая ММ воспроизводиталгоритм («логику») функционирования исследуемой системы во времени приразличных сочетаниях значений параметров системы и внешней среды.

Примером простейшей аналитической модели может служить уравнениепрямолинейного равномерного движения. При исследовании такого процессас помощью имитационной модели должно быть реализовано наблюдениеза изменением пройденного пути с течением времени.Очевидно, в одних случаях более предпочтительным являетсяаналитическое моделирование, в других - имитационное (или сочетание того идругого). Чтобы выбор был удачным, необходимо ответить на два вопроса.

С какой целью проводится моделирование?

К какому классу может быть отнесено моделируемое явление?

Ответы на оба эти вопроса могут быть получены в ходе выполнения двухпервых этапов моделирования.

Имитационные модели не только по свойствам, но и по структуресоответствуют моделируемому объекту. При этом имеется однозначное и явноесоответствие между процессами, получаемыми на модели, и процессами,протекающими на объекте. Недостатком имитационного моделированияявляется большое время решения задачи для получения хорошей точности.

Результаты имитационного моделирования работы стохастическойсистемы являются реализациями случайных величин или процессов. Поэтомудля нахождения характеристик системы требуется многократное повторение ипоследующая обработка данных. Чаще всего в этом случае применяетсяразновидность имитационного моделирования - статистическое

моделирование (или метод Монте-Карло), т.е. воспроизведение в моделяхслучайных факторов, событий, величин, процессов, полей.

По результатам статистического моделирования определяют оценкивероятностных критериев качества, общих и частных, характеризующихфункционирование и эффективность управляемой системы. Статистическоемоделирование широко применяется для решения научных и прикладных задачв различных областях науки и техники. Методы статистическогомоделирования широко применяются при исследовании сложныхдинамических систем, оценке их функционирования и эффективности.

Заключительный этап статистического моделирования основан наматематической обработке полученных результатов. Здесь используют методыматематической статистики (параметрическое и непараметрическое оценивание,проверку гипотез). Примером параметрической оценки являетсявыборочное среднее показателя эффективности. Среди непараметрическихметодов большое распространение получил метод гистограмм .

Рассмотренная схема основана на многократных статистическихиспытаниях системы и методах статистики независимых случайных величин.Эта схема является далеко не всегда естественной на практике и оптимальнойпо затратам. Сокращение времени испытания систем может быть достигнуто засчет использования более точных методов оценивания. Как известно изматематической статистики, наибольшую точность при заданном объемевыборки имеют эффективные оценки. Оптимальная фильтрация и методмаксимального правдоподобия дают общий метод получения таких оценок.В задачах статистического моделирования обработка реализацийслучайных процессов необходима не только для анализа выходных процессов.

Весьма важен также и контроль характеристик входных случайныхвоздействий. Контроль заключается в проверке соответствия распределенийгенерируемых процессов заданным распределениям. Эта задача частоформулируется как задача проверки гипотез .

Общей тенденцией моделирования с использованием ЭВМ у сложныхуправляемых систем является стремление к уменьшению временимоделирования, а также проведение исследований в реальном масштабевремени. Вычислительные алгоритмы удобно представлять в рекуррентнойформе, допускающей их реализацию в темпе поступления текущей информации.

ПРИНЦИПЫ СИСТЕМНОГО ПОДХОДА В МОДЕЛИРОВАНИИ

    Основные положения теории систем

Основные положения теории систем возникли в ходе исследованиядинамических систем и их функциональных элементов. Под системой понимают группу взаимосвязанных элементов, действующих совместнос целью выполнения заранее поставленной задачи. Анализ систем позволяетопределить наиболее реальные способы выполнения поставленной задачи,обеспечивающие максимальное удовлетворение поставленных требований.

Элементы, составляющие основу теории систем, не создаются с помощьюгипотез, а обнаруживаются экспериментальным путем. Для того чтобы начатьпостроение системы, необходимо иметь общие характеристикитехнологических процессов. Это же справедливо и в отношении принциповсоздания математически сформулированных критериев, которым долженудовлетворять процесс или его теоретическое описание. Моделированиеявляется одним из наиболее важных методов научного исследования иэкспериментирования.

При построении моделей объектов используется системный подход,представляющий собой методологию решения сложных задач, в основекоторой лежит рассмотрение объекта как системы, функционирующейв некоторой среде. Системный подход предполагает раскрытие целостностиобъекта, выявление и изучение его внутренней структуры, а также связейс внешней средой. При этом объект представляется как часть реального мира,которая выделяется и исследуется в связи с решаемой задачей построениямодели. Кроме этого, системный подход предполагает последовательныйпереход от общего к частному, когда в основе рассмотрения лежит цельпроектирования, а объект рассматривается во взаимосвязи с окружающейсредой.

Сложный объект может быть разделен на подсистемы, представляющие собой части объекта, удовлетворяющие следующим требованиям:

1) подсистема является функционально независимой частью объекта. Онасвязана с другими подсистемами, обменивается с ними информацией иэнергией;

2) для каждой подсистемы могут быть определены функции или свойства,не совпадающие со свойствами всей системы;

3) каждая из подсистем может быть подвергнута дальнейшему делению доуровня элементов.

В данном случае под элементом понимается подсистема нижнего уровня,дальнейшее деление которой нецелесообразно с позиций решаемой задачи.

Таким образом, систему можно определить как представление объектав виде набора подсистем, элементов и связей с целью его создания,исследования или усовершенствования. При этом укрупненное представлениесистемы, включающее в себя основные подсистемы и связи между ними,называется макроструктурой, а детальное раскрытие внутреннего строениясистемы до уровня элементов – микроструктурой.

Наряду с системой обычно существует надсистема – система болеевысокого уровня, в состав которой входит рассматриваемый объект, причёмфункция любой системы может быть определена только через надсистему.

Следует выделить понятие среды как совокупности объектов внешнего мира,существенно влияющих на эффективность функционирования системы, но невходящих в состав системы и ее надсистемы.

В связи с системным подходом к построению моделей используетсяпонятие инфраструктуры, описывающей взаимосвязи системы с ееокружением (средой).При этом выделение, описание и исследование свойств объекта,существенных в рамках конкретной задачи называется стратификациейобъекта, а всякая модель объекта является его стратифицированнымописанием.

Для системного подхода важным является определение структуры системы, т.е. совокупности связей между элементами системы, отражающих ихвзаимодействие. Для этого вначале рассмотрим структурный ифункциональный подходы к моделированию.

При структурном подходе выявляются состав выделенных элементов системы и связи между ними. Совокупность элементов и связей позволяет судить о структуре системы. Наиболее общим описанием структуры является топологическое описание. Оно позволяет определить составные части системыи их связи с помощью графов. Менее общим является функциональное описание, когда рассматриваютсяо тдельные функции, т. е. алгоритмы поведения системы. При этом реализуетсяфункциональный подход, определяющий функции, которые выполняетсистема.

На базе системного подхода может быть предложена последовательностьразработки моделей, когда выделяют две основные стадии проектирования:макропроектирование и микропроектирование.

На стадии макропроектирования строится модель внешней среды,выявляются ресурсы и ограничения, выбирается модель системы и критериидля оценки адекватности.

Стадия микропроектирования в значительной степени зависит отконкретного типа выбранной модели. В общем случае предполагает созданиеинформационного, математического, технического и программногообеспечения системы моделирования. На этой стадии устанавливаютсяосновные технические характеристики созданной модели, оцениваются времяработы с ней и затраты ресурсов для получения заданного качества модели.

Независимо от типа модели при ее построении необходиморуководствоваться рядом принципов системного подхода:

1) последовательное продвижение по этапам создания модели;

2) согласование информационных, ресурсных, надежностных и другиххарактеристик;

3) правильное соотношение различных уровней построения модели;

4) целостность отдельных стадий проектирования модели.

Математическое моделирование

1. Что такое математическое моделирование?

С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как «математическая экономика», «математическая химия», «математическая лингвистика» и т. д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Математическая модель - это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования - исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование - это еще и метод познания окружающего мира, дающий возможность управлять им.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, «что было бы, если бы...» Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

2. Основные этапы математического моделирования

1) Построение модели . На этом этапе задается некоторый «нематематический» объект - явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.

2) Решение математической задачи, к которой приводит модель . На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.

5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

3. Классификация моделей

Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие - как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т. д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф - это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).

По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.

4. Примеры математических моделей

1) Задачи о движении снаряда.

Рассмотрим следующую задачу механики.

Снаряд пущен с Земли с начальной скоростью v 0 = 30 м/с под углом a = 45° к ее поверхности; требуется найти траекторию его движения и расстояние S между начальной и конечной точкой этой траектории.

Тогда, как это известно из школьного курса физики, движение снаряда описывается формулами:

где t - время, g = 10 м/с 2 - ускорение свободного падения. Эти формулы и дают математическую модель поставленной задачи. Выражая t через x из первого уравнения и подставляя во второе, получим уравнение траектории движения снаряда:

Эта кривая (парабола) пересекает ось x в двух точках: x 1 = 0 (начало траектории) и (место падения снаряда). Подставляя в полученные формулы заданные значения v0 и a, получим

ответ: y = x – 90x 2 , S = 90 м.

Отметим, что при построении этой модели использован ряд предположений: например, считается, что Земля плоская, а воздух и вращение Земли не влияют на движение снаряда.

2) Задача о баке с наименьшей площадью поверхности.

Требуется найти высоту h 0 и радиус r 0 жестяного бака объема V = 30 м 3 , имеющего форму закрытого кругового цилиндра, при которых площадь его поверхности S минимальна (в этом случае на его изготовление пойдет наименьшее количество жести).

Запишем следующие формулы для объема и площади поверхности цилиндра высоты h и радиуса r:

V = p r 2 h, S = 2p r(r + h).

Выражая h через r и V из первой формулы и подставляя полученное выражение во вторую, получим:

Таким образом, с математической точки зрения, задача сводится к определению такого значения r, при котором достигает своего минимума функция S(r). Найдем те значения r 0 , при которых производная

обращается в ноль:Можно проверить, что вторая производная функции S(r) меняет знак с минуса на плюс при переходе аргумента r через точку r 0 . Следовательно, в точке r0 функция S(r) имеет минимум. Соответствующее значение h 0 = 2r 0 . Подставляя в выражение для r 0 и h 0 заданное значение V, получим искомый радиус и высоту

3) Транспортная задача.

В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозят 50 т муки, а со второго - 70 т на заводы, причем на первый - 40 т, а на второй - 80 т.

Обозначим через a ij стоимость перевозки 1 т муки с i-го склада на j-й завод (i, j = 1,2). Пусть

a 11 = 1,2 р., a 12 = 1,6 р., a 21 = 0,8 р., a 22 = 1 р.

Как нужно спланировать перевозки, чтобы их стоимость была минимальной?

Придадим задаче математическую формулировку. Обозначим через x 1 и x 2 количество муки, которое надо перевезти с первого склада на первый и второй заводы, а через x 3 и x 4 - со второго склада на первый и второй заводы соответственно. Тогда:

x 1 + x 2 = 50, x 3 + x 4 = 70, x 1 + x 3 = 40, x 2 + x 4 = 80. (1)

Общая стоимость всех перевозок определяется формулой

f = 1,2x 1 + 1,6x 2 + 0,8x 3 + x 4 .

С математической точки зрения, задача заключается в том, чтобы найти четыре числа x 1 , x 2 , x 3 и x 4 , удовлетворяющие всем заданным условиям и дающим минимум функции f. Решим систему уравнений (1) относительно xi (i = 1, 2, 3, 4) методом исключения неизвестных. Получим, что

x 1 = x 4 – 30, x 2 = 80 – x 4 , x 3 = 70 – x 4 , (2)

а x 4 не может быть определено однозначно. Так как x i і 0 (i = 1, 2, 3, 4), то из уравнений (2) следует, что 30Ј x 4 Ј 70. Подставляя выражение для x 1 , x 2 , x 3 в формулу для f, получим

f = 148 – 0,2x 4 .

Легко видеть, что минимум этой функции достигается при максимально возможном значении x 4 , то есть при x 4 = 70. Соответствующие значения других неизвестных определяются по формулам (2): x 1 = 40, x 2 = 10, x 3 = 0.

4) Задача о радиоактивном распаде.

Пусть N(0) - исходное количество атомов радиоактивного вещества, а N(t) - количество нераспавшихся атомов в момент времени t. Экспериментально установлено, что скорость изменения количества этих атомов N"(t) пропорциональна N(t), то есть N"(t)=–l N(t), l >0 - константа радиоактивности данного вещества. В школьном курсе математического анализа показано, что решение этого дифференциального уравнения имеет вид N(t) = N(0)e –l t . Время T, за которое число исходных атомов уменьшилось вдвое, называется периодом полураспада, и является важной характеристикой радиоактивности вещества. Для определения T надо положить в формуле Тогда Например, для радона l = 2,084 · 10 –6 , и следовательно, T = 3,15 сут.

5) Задача о коммивояжере.

Коммивояжеру, живущему в городе A 1 , надо посетить города A 2 , A 3 и A 4 , причем каждый город точно один раз, и затем вернуться обратно в A 1 . Известно, что все города попарно соединены между собой дорогами, причем длины дорог b ij между городами A i и A j (i, j = 1, 2, 3, 4) таковы:

b 12 = 30, b 14 = 20, b 23 = 50, b 24 = 40, b 13 = 70, b 34 = 60.

Надо определить порядок посещения городов, при котором длина соответствующего пути минимальна.

Изобразим каждый город точкой на плоскости и пометим ее соответствующей меткой Ai (i = 1, 2, 3, 4). Соединим эти точки отрезками прямых: они будут изображать дороги между городами. Для каждой «дороги» укажем ее протяженность в километрах (рис. 2). Получился граф - математический объект, состоящий из некоторого множества точек на плоскости (называемых вершинами) и некоторого множества линий, соединяющих эти точки (называемых ребрами). Более того, этот граф меченый, так как его вершинам и ребрам приписаны некоторые метки - числа (ребрам) или символы (вершинам). Циклом на графе называется последовательность вершин V 1 , V 2 , ..., V k , V 1 такая, что вершины V 1 , ..., V k - различны, а любая пара вершин V i , V i+1 (i = 1, ..., k – 1) и пара V 1 , V k соединены ребром. Таким образом, рассматриваемая задача заключается в отыскании такого цикла на графе, проходящего через все четыре вершины, для которого сумма всех весов ребер минимальна. Найдем перебором все различные циклы, проходящие через четыре вершины и начинающиеся в A 1:

1) A 1 , A 4 , A 3 , A 2 , A 1 ;
2) A 1 , A 3 , A 2 , A 4 , A 1 ;
3) A 1 , A 3 , A 4 , A 2 , A 1 .

Найдем теперь длины этих циклов (в км): L 1 = 160, L 2 = 180, L 3 = 200. Итак, маршрут наименьшей длины - это первый.

Заметим, что если в графе n вершин и все вершины попарно соединены между собой ребрами (такой граф называется полным), то число циклов, проходящих через все вершины, равно Следовательно, в нашем случае имеется ровно три цикла.

6) Задача о нахождении связи между структурой и свойствами веществ.

Рассмотрим несколько химических соединений, называемых нормальными алканами. Они состоят из n атомов углерода и n + 2 атомов водорода (n = 1, 2 ...), связанных между собой так, как показано на рисунке 3 для n = 3. Пусть известны экспериментальные значения температур кипения этих соединений:

y э (3) = – 42°, y э (4) = 0°, y э (5) = 28°, y э (6) = 69°.

Требуется найти приближенную зависимость между температурой кипения и числом n для этих соединений. Предположим, что эта зависимость имеет вид

y » a n + b,

где a , b - константы, подлежащие определению. Для нахождения a и b подставим в эту формулу последовательно n = 3, 4, 5, 6 и соответствующие значения температур кипения. Имеем:

– 42 » 3a + b, 0 » 4a + b, 28 » 5a + b, 69 » 6a + b.

Для определения наилучших a и b существует много разных методов. Воспользуемся наиболее простым из них. Выразим b через a из этих уравнений:

b » – 42 – 3a , b » – 4a , b » 28 – 5a , b » 69 – 6a .

Возьмем в качестве искомого b среднее арифметическое этих значений, то есть положим b » 16 – 4,5a . Подставим в исходную систему уравнений это значение b и, вычисляя a , получим для a следующие значения: a » 37, a » 28, a » 28, a » 36. Возьмем в качестве искомого a среднее значение этих чисел, то есть положим a » 34. Итак, искомое уравнение имеет вид

y » 34n – 139.

Проверим точность модели на исходных четырех соединениях, для чего вычислим температуры кипения по полученной формуле:

y р (3) = – 37°, y р (4) = – 3°, y р (5) = 31°, y р (6) = 65°.

Таким образом, ошибка расчетов данного свойства для этих соединений не превышает 5°. Используем полученное уравнение для расчета температуры кипения соединения с n = 7, не входящего в исходное множество, для чего подставим в это уравнение n = 7: y р (7) = 99°. Результат получился довольно точный: известно, что экспериментальное значение температуры кипения y э (7) = 98°.

7) Задача об определении надежности электрической цепи.

Здесь мы рассмотрим пример вероятностной модели. Сначала приведем некоторые сведения из теории вероятностей - математической дисциплины, изучающей закономерности случайных явлений, наблюдаемых при многократном повторении опыта. Назовем случайным событием A возможный исход некоторого опыта. События A 1 , ..., A k образуют полную группу, если в результате опыта обязательно происходит одно из них. События называются несовместными, если они не могут произойти одновременно в одном опыте. Пусть при n-кратном повторении опыта событие A произошло m раз. Частотой события A называется число W = . Очевидно, что значение W нельзя предсказать точно до проведения серии из n опытов. Однако природа случайных событий такова, что на практике иногда наблюдается следующий эффект: при увеличении числа опытов значение практически перестает быть случайным и стабилизируется около некоторого неслучайного числа P(A), называемого вероятностью события A. Для невозможного события (которое никогда не происходит в опыте) P(A)=0, а для достоверного события (которое всегда происходит в опыте) P(A)=1. Если события A 1 , ..., A k образуют полную группу несовместимых событий, то P(A 1)+...+P(A k)=1.

Пусть, например, опыт состоит в подбрасывании игральной кости и наблюдении числа выпавших очков X. Тогда можно ввести следующие случайные события A i ={X = i}, i = 1, ..., 6. Они образуют полную группу несовместных равновероятных событий, поэтому P(A i) = (i = 1, ..., 6).

Суммой событий A и B называется событие A + B, состоящее в том, что в опыте происходит хотя бы одно из них. Произведением событий A и B называется событие AB, состоящее в одновременном появлении этих событий. Для независимых событий A и B верны формулы

P(AB) = P(A) P(B), P(A + B) = P(A) + P(B).

8) Рассмотрим теперь следующую задачу . Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны P 1 = 0,1, P 2 = 0,15, P 3 = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли данная цепь надежной.

Так как элементы включены последовательно, то тока в цепи не будет (событие A), если откажет хотя бы один из элементов. Пусть A i - событие, заключающееся в том, что i-й элемент работает (i = 1, 2, 3). Тогда P(A1) = 0,9, P(A2) = 0,85, P(A3) = 0,8. Очевидно, что A 1 A 2 A 3 - событие, заключающееся в том, что одновременно работают все три элемента, и

P(A 1 A 2 A 3) = P(A 1) P(A 2) P(A 3) = 0,612.

Тогда P(A) + P(A 1 A 2 A 3) = 1, поэтому P(A) = 0,388 < 0,4. Следовательно, цепь является надежной.

В заключение отметим, что приведенные примеры математических моделей (среди которых есть функциональные и структурные, детерминистические и вероятностные) носят иллюстративный характер и, очевидно, не исчерпывают всего разнообразия математических моделей, возникающих в естественных и гуманитарных науках.

Существует несколько подходов к выделению основных этапов математического моделирования. Приведем некоторые из них.

В. И. Крутова и В. В. Попова выделяют два основных этапа . Первым этапом математического моделирования является постановка задачи, определение объекта и целей исследования, задание критериев (признаков) изучения объектов и управления ими. Неправильная или неполная постановка задачи может свести на нет результаты всех последующих этапов.

Вторым этапом моделирования является выбор типа математической модели, что является важнейшим моментом, определяющим направление всего исследования. Обычно последовательно строится несколько моделей. Сравнение результатов их исследования с реальностью позволяет установить наилучшую из них. На этапе выбора типа математической модели при помощи анализа данных поискового эксперимента устанавливаются: линейность или нелинейность, динамичность или статичность, стационарность или нестационарность, а также степень детерминированности исследуемого объекта или процесса.

Процесс выбора математической модели объекта заканчивается ее предварительным контролем, который также является первым шагом на пути к исследованию модели. При этом осуществляются следующие виды контроля (проверки): размерностей, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, математической замкнутости, физического (экономического, биологического и др.) смысла, устойчивости модели .

Поясним, что это подразумевает:

· контроль размерностей сводится к проверке выполнения правила, согласно которому приравниваться и складываться могут только величины одинаковой размерности;

· контроль порядков величин направлен на упрощение модели. При этом определяются порядки складываемых величин и явно малозначительные слагаемые отбрасываются;

· анализ характера зависимостей сводится к проверке направления и скорости изменения одних величин при изменении других. Направления и скорость, вытекающие из математической модели, должны соответствовать физическому смыслу задачи;

· анализ экстремальных ситуаций сводится к проверке наглядного смысла решения при приближении параметров модели к нулю или бесконечности;

· контроль граничных условий состоит в том, что проверяется соответствие математической модели граничным условиям, вытекающим из смысла задачи. При этом проверяется, действительно ли граничные условия поставлены и учтены при построении искомой функции и что эта функция на самом деле удовлетворяет таким условиям;

· анализ математической замкнутости сводится к проверке того, что математическая модель дает однозначное решение;

· анализ физического смысла сводится к проверке физического содержания промежуточных соотношений, используемых при построении математической модели;

· проверка устойчивости модели состоит в проверке того, что варьирование исходных данных в рамках имеющихся данных о реальном объекте не приведет к существенному изменению решения.

С.А. Айвазян, И.С. Енюков и Л.Д. Мешалкин выделяют шесть основных этапов моделирования .

1. Исходный этап. На этом этапе осуществляется определение конечных целей моделирования, отбор показателей, включаемых в модель, разделение их на входные и выходные.

2. Формирование априорной информации, т.е. постулирование, математическая формализация и, по возможности, экспериментальная проверка исходных допущений, относящихся к качественному характеру изучаемого явления.

3. Собственно моделирование. На этом этапе устанавливают общий вид модели (структуру, аналитическую и символьную запись).

4. Статистический анализ модели – оценивание неизвестных параметров, входящих в аналитическую запись модели, исследование свойств полученных статистических оценок.

5. Анализ адекватности модели. Заключается в применении различных процедур сопоставления выводов, оценок, следствий, полученных по результатам анализа модели и реально наблюдаемой действительностью.

6. Этап уточнения модели. Проводится лишь в том случае, если необходимы уточняющие исследования, развитие и углубление информации.

Еще один подход к выделению этапов математического моделирования, представленный В.П. Трусовым, изображен на схеме (Рис. 7).

Поясним выделенные на схеме основные этапы.

1. Обследование объекта моделирования означает, что математические модели, особенно использующие численные методы, требуют для своего построения значительных интеллектуальных, финансовых и временных затрат. Поэтому решение о разработке новой модели принимается лишь в случае отсутствия иных, более простых путей решения возникших проблем (например, модификации одной из существующих моде­лей). Основной целью обследования объекта моделирования является подго­товка содержательной постановки задачи моделирования, т.е. списка основных вопросов об объекте моделирования, интересующих за­казчика.

Приведем пример содержательной по­становки задачи о баскетболисте: необходимо разработать математическую модель, позволяющую описать по­лет баскетбольного мяча, брошенного игроком в баскетбольную кор­зину.

Модель должна обеспечить решение следующих задач: вычислять положение мяча в любой момент времени, определять точность попадания мяча в корзину после броска при различных начальных параметрах.

Исходные данные: масса и радиус мяча; начальные координаты, начальная скорость и угол броска мяча; координаты центра и радиус корзины.

1. Концептуальная постановка задачи – это сфор­мулированный в терминах конкретных дисциплин (физики, химии, био­логии и т.д.) перечень основных вопросов, интересующих заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования. Концептуальная постановка позволяет сформули­ровать математическую постановку задачи моделирования, т.е. со­вокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

Для контроля правильности полученной системы математичес­ких соотношений требуется проведение ряда обязательных прове­рок (о них упоминают также В. И. Крутова и В. В. Попова):

· Контроль размерностей, включающий правило, согласно ко­торому приравниваться и складываться могут только вели­чины одинаковой размерности.

· Контроль порядков, состоящий из грубой оценки сравнитель­ных порядков складываемых величин и исключением мало­значимых параметров.

· Контроль характера зависимостей заключается в проверке того, что направление и скорость изменения выходных па­раметров модели, вытекающие из математичес­ких соотношений, такие, как это следует непосредственно из «физического» смысла изучаемой модели.

· Контроль экстремальных ситуаций – проверка того, какой вид принимают математические соотношения, а также результа­ты моделирования, если параметры модели или их комби­нации приближаются к предельно допустимым зна­чениям, чаще всего к нулю или бесконечности. В подобных экстремальных ситуациях модель часто упрощается, матема­тические соотношения приобретают более наглядный смысл, упрощается их проверка.

· Контроль граничных условий, включающий проверку того, что граничные условия действительно наложены, что они ис­пользованы в процессе построения искомого решения и что значения выходных параметров модели на самом деле удов­летворяют данным условиям.

· Контроль физического смысла - проверка физического или иного смысла исходных и промежуточных соотношений.

· Контроль математической замкнутости, состоящий в про­верке того, что выписанная система математических соотно­шений дает возможность, притом однозначно, решить по­ставленную математическую задачу. Например, если задача свелась к отысканию n неизвестных из некоторой системы алгебраических уравнений, то контроль замкнутости состоит в проверке того, что число неза­висимых уравнений должно быть n . Если их меньше n , то надо установить недостающие уравнения, а если их больше n , то либо уравнения зависимы, либо при их составлении допущена ошибка. Однако если уравнения получаются из эксперимента или в результате наблюдений, то возможна постановка задачи, при которой число уравнений превыша­ет n , но сами уравнения удовлетворяются лишь приближен­но, а решение ищется, например, по методу наименьших квадратов

3. Понятие корректности задачи имеет большое значение в при­кладной математике. Например, численные методы решения оправ­дано применять лишь к корректно поставленным задачам. Дока­зательство корректности конкретной математической задачи - до­статочно сложная проблема. Математическая модель является корректной, если для нее осу­ществлен и получен положительный результат всех контрольных проверок размерности, порядков, характера зависимостей, экстре­мальных ситуаций, граничных условий, физического смысла и ма­тематической замкнутости.

4. Выбор и обоснование методов решения задачи.

При использовании разработанных математических моделей, как правило, требуется найти зависимость некоторых неизвестных заранее параметров объекта моделирования (например, координат и скорости центра масс тела), удовлетворяющих определенной системе уравнений. Таким образом, поиск решения задачи сводится к отысканию некоторых зависимостей искомых величин от исходных параметров модели. Все методы решения задач, составляющих «ядро» математи­ческих моделей, можно подразделить на аналитические и алгорит­мические.

Аналитические методы более удобны для пос­ледующего анализа результатов, но применимы лишь для относи­тельно простых моделей. В случае, если математическая задача допускает аналитическое решение, оно, без сомнения, предпочтительнее численного.

Алгорит­мические методы сводятся к некоторому алгоритму, ре­ализующему вычислительный эксперимент с использованием ЭВМ. Точность моделирования в подобном эксперименте существенно за­висит от выбранного метода и его параметров (например, шага ин­тегрирования). Алгоритмические методы, как правило, более тру­доемки в реализации, требуют обширной библиотеки специального программного обеспечения и мощной вычислитель­ной техники.

Общим для всех численных методов является сведение мате­матической задачи к конечномерной. Это чаще всего достига­ется дискретизацией исходной задачи, т.е. переходом от функции непрерывного аргумента к функциям дискретного аргумента. На­пример, траектория центра тяжести баскетбольного мяча опреде­ляется не как непрерывная функция времени, а как дискретная функция координат от времени. Полученное решение дискретной задачи принимается за прибли­женное решение исходной математической задачи.

6. Проверка адекватности модели.

Под адекватностью математической модели понимается степень соответствия результатов моделирования – экспериментальным данным или тестовой задаче.

Проверка адекватности модели преследует две цели: убедиться в справедливости гипотез, принятых на этапах концептуальной и математической постано­вок и установить, что точность полученных результатов соответ­ствует точности, оговоренной в техническом задании.

Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хорошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором – о сравне­нии с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требо­ваний, предъявляемых к модели, и ее назначения. В моделях, пред­назначенных для выполнения оценочных расчетов, удовлетворительной считается точность 10 - 15 %. В моделях, исполь­зуемых в управляющих системах, требуемая точность может быть 1 - 2% и даже более.

Как правило, различают качественное и количественное совпа­дение результатов сравнения. При качественном сравнении требуется лишь совпадение некоторых характерных особенностей исследуемых параметров (например, наличие экстре­мальных точек, возрастание или убывание параметра). При количествен­ном сравнении большое значение следует придавать точности ис­ходных данных для моделирования и соответствующих им значе­ний сравниваемых параметров.

7. Практическое использование построенной модели.

Независимо от того, в какой области применима построенная модель, необходим количественный и качественный анализ результатов моделирования.

Всесторонний анализ результатов мо­делирования позволяет:

· выполнить модификацию рассматриваемого объекта, найти его оптимальные характеристики или, по крайней мере, луч­шим образом учесть его поведение и свойства;

· обозначить область применения модели, что особенно важ­но в случае использования моделей для систем автоматичес­кого управления;

· проверить обоснованность гипотез, принятых на этапе мате­матической постановки, оценить возможность упрощения модели с целью повышения ее эффективности при сохране­нии требуемой точности;

· показать, в каком направлении следует развивать модель в дальнейшем.

Вышеописанную В.П. Трусовым периодизацию основных этапов математического моделирования, мы считаем наиболее содержательной и полной.

Исследуя научную литературу, мы выделили основные этапы математического моделирования, которые выделены у ряда ученых:

1) Построение модели. Задается некоторый «нематематический» объект – явление природы, конструкция, экономический план, производственный процесс и т. д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель.

2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи, в том числе на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах установленной точности.

5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ 2. КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Методы научного познания. Место моделирования среди методов познания. Модели в науке и технике. Классификация математических моделей в зависимости: - от сложности объекта моделирования; - от оператора модели; - от параметров модели; - от методов реализации; - от целей моделирования. Классификация математических моделей технических объектов. Типовая схема проектирования технического объекта в САПР. Методология математического моделирования (вычислительный эксперимент)

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ. МЕСТО МОДЕЛИРОВАНИЯ СРЕДИ МЕТОДОВ ПОЗНАНИЯ. Метафизический Общенаучные Всеобщие МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ Диалектический Частнонаучные Общие Эмпирические Теоретические Анализ Наблюдение Абстрагирование Синтез Эксперимент Идеализация Аналогия Измерение Формализация Моделирование Индукция Дедукция Изучением методов познания окружающего мира занимается методология. Основная задача методологии изучение происхождения, сущности, эффективности и других характеристик методов познания. Метод – совокупность приемов и операций практического и теоретического освоения действительности. Владеть методом – значит знать, каким образом, в какой последовательности нужно совершать те или иные действия для решения различных задач, и уметь реализовать эти знания на практике. Моделирование – метод познания окружающего мира, относящийся к общенаучным методам; он применяется как на эмпирическом, так и на теоретическом уровне познания.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МЕТОДОВ МОДЕЛИРОВАНИЯ. Физическое Аналоговое Материальное моделирование ОБЪЕКТ МОДЕЛИРОВАНИЯ Идеальное моделирование Интуитивное Научное Знаковое моделирование При физическом моделировании реальному объекту ставится в соответствие его (увеличенный или уменьшенный) материальный аналог, допускающий исследование в лабораторных условиях; свойства изучаемых процессов и явлений переносятся затем с модели на объект на основе теории подобия. Аналоговое моделирование - это моделирование, основанное на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими соотношениями, логическими и структурными схемами). Интуитивное моделирование основано на интуитивном (не обоснованном с позиций формальной логики) представлении об объекте исследования, не поддающемся формализации или не нуждающемся в ней. Научное моделирование - это всегда логически обоснованное моделирование, использующее минимальное число предположений, принятых в качестве гипотез на основании наблюдений за объектом моделирования. Математическое моделирование - это идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ И ВЗАИМОСВЯЗЬ МОДЕЛЕЙ (УРОВНИ МОДЕЛИРОВАНИЯ) При наблюдении за объектом-оригиналом в голове исследователя формируется некий мысленный образ объекта, его идеальная модель, которую в научной литературе принято называть когнитивной (мысленной) моделью. ОБЪЕКТ МОДЕЛИРОВАНИЯ Когнитивная модель Представление когнитивной модели на естественном языке называется содержательной моделью. Содержательная модель Когнитивная модель Описательная Объяснительная Предсказательная Концептуальная модель Материальное моделирование Причинно. Логико. Структурносемантическая функциональная следственная Формальная модель Математическая Информационная Концептуальной моделью принято называть содержательную модель, при формулировке которой используются понятия и представления предметных областей знаний, занимающихся изучением объекта моделирования. В более широком смысле под концептуальной моделью понимают содержательную модель, базирующуюся на определенной концепции или точке зрения. Формальная модель является представлением концептуальной модели с помощью одного или нескольких формальных языков (например, языков математических теорий или алгоритмических языков). Математическая модель – совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МОДЕЛИ В НАУКЕ И ТЕХНИКЕ В научной и технической литературе понятие модель чаще всего употребляется в следующем смысле: модель - аналог (чертеж, график, план, схема, описание) реального объекта; модель - образец (уменьшенный, увеличенный, в натуральную величину) будущего изделия. Под моделью понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект-оригинал, сохраняя основные важные для данного исследования черты оригинала. Процесс построения, исследования и использования модели называется моделированием. Свойства математических моделей: адекватность; полнота, замкнутость, внутренняя непротиворечивость; простота и наглядность; потенциальность (возможности модели с точки зрения получения новых знаний об объекте исследования); устойчивость (или робастность, грубость); точность; экономичность; универсальность. Если результаты моделирования удовлетворяют исследователя и могут служить основой для прогнозирования поведения или свойств исследуемого объекта, то говорят, что модель адекватна объекту. Другими словами, под адекватностью математической модели понимают правильное качественное и достаточное количественное описание тех характеристик объекта моделирования, которые важны в данном конкретном исследовании. Адекватность модели зависит от целей моделирования и принятых критериев.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ УНИВЕРСАЛЬНОСТЬ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Одна и та же математическая модель находит подчас самые различные приложения. Например, с помощью модели, содержащей уравнение Пуассона можно изучать - установившееся течение (несжимаемой) жидкости; - стационарные тепловые поля; - распределение электрического потенциала; - механические напряжения при кручении стержней; - деформацию тонкой мембраны; - фильтрацию нефти в нефтеносном пласте или влаги в почве; - диффузию посторонней примеси в твердом теле, жидкости или газе; - распространение эпидемии в регионе. В каждой из перечисленных задач функции и приобретают свой содержательный смысл, однако их связь описывается общим для всех задач уравнением Пуассона. Если правая часть обращается в нуль, рассматриваемое уравнение называется уравнением Лапласа:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗАЧЕМ НУЖНА МОДЕЛЬ? ЦЕЛИ МОДЕЛИРОВАНИЯ Модель нужна для того, чтобы: понять, как устроен конкретный объект: какова его структура, основные свойства, законы развития и взаимодействия с окружающей средой; научиться управлять объектом или процессом, находить оптимальные способы управления при заданных целях и критериях; прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект. Хорошо построенная модель, как правило, доступнее, информативнее и удобнее для исследователя, нежели реальный объект. Практическое использование математической модели (экспериментирование с моделью), аналогично проведению экспериментов с реальным объектом, но вместо физического (лабораторного, натурного) эксперимента с реальным объектом проводится вычислительный эксперимент с его моделью. Прямой натурный эксперимент часто дорог, трудоемок, опасен или попросту невозможен. Работа не с самим объектом, а с его моделью позволяет относительно быстро и без существенных затрат исследовать свойства и поведение объекта в любых мыслимых ситуациях. Эксперименты на моделях с применением ЭВМ позволяют разработать план натурных экспериментов, выяснить требуемые характеристики измерительной аппаратуры, наметить сроки проведения наблюдений, оценить стоимость эксперимента.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СТРУКТУРА МАТЕМАТИЧЕСКОЙ МОДЕЛИ Математическая модель - это любой оператор, позволяющий по значениям входных параметров из области допустимых значений установить выходные значения параметров объекта моделирования: Здесь и - множества допустимых значений входных и выходных параметров для моделируемого объекта. В зависимости от природы, моделируемого объекта элементами множеств и могут являться любые математические объекты (числа, векторы, тензоры, функции, множества и т. п.). Оператор - это: – некоторая функция, связывающая входные и выходные значения, – отображение (оператор), представляющее символическую запись системы алгебраических, дифференциальных, интегро-дифференциальных или интегральных уравнений, – некоторый алгоритм (совокупность правил, таблиц), обеспечивающих определение выходных параметров по заданным исходным значениям.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (в зависимости от сложности объекта моделирования) ОБЪЕКТ МОДЕЛИРОВАНИЯ Простой объект Имитационная модель Система Структурная модель Функциональная модель Структурно-функциональная модель · Объект моделирования - это некоторое материальное тело (конструкция, техническое устройство, агрегат, узел, деталь и т. п.), - физическое явление, - природный, технологический или социальный процесс. · Все объекты моделирования можно разделить на две группы: простые и объектысистемы. Объект является простым, если при моделировании не рассматривается его внутреннее строение, не выделяются составляющие его элементы или подпроцессы (например, материальная точка в классической механике – простой объект). · Система есть совокупность взаимосвязанных элементов, в определенном смысле обособленная от окружающей среды и взаимодействующая с ней как целое.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (в зависимости от оператора модели) Линейный Нелинейный ОПЕРАТОР МОДЕЛИ Алгоритмический Сложный Простой Функция ОДУ РУ СЛАУ СОДУ ДУЧП ИДУ ОДУ – обыкновенное дифференциальное уравнение, РУ – разностное уравнение, СЛАУ – система линейных алгебраических уравнений, СОДУ – система обыкновенных дифференциальных уравнений, ДУЧП - дифференциальные уравнения в частных производных, ИДУ – интегро-дифференциальные уравнения.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (в зависимости от параметров модели) Стохастические Случайные Интервальные Детерминированные Нечеткие Неопределенные ПАРАМЕТРЫ И ПЕРЕМЕННЫЕ МОДЕЛИРОВАНИЯ По отношению ко времени По отношению к размерности пространства Динамические Статические Стационарные Одномерные Нестационарные Двухмерные Трехмерные По составу параметров Дискретные Качественные Непрерывные Количественные Смешанные

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (в зависимости от методов реализации модели) МЕТОДЫ ИССЛЕДОВАНИЯ МОДЕЛИ Аналитические Алгоритмические Алгебраические Численные Приближенные Имитационные Метод исследования модели относят к аналитическим, если он позволяет получить выходные величины в виде аналитических выражений. При алгоритмическом подходе задается некоторый алгоритм, преобразующий (за конечное число шагов) входные данные в искомое решение. При численном подходе (МКР, МКЭ) производится дискретизация исходных математических соотношений, то есть переход от функций непрерывного аргумента к функциям дискретного аргумента. Полученное решение дискретной задачи принимается за приближенное решение исходной математической задачи. При имитационном подходе на отдельные элементы разбивается сам объект исследования. В этом случае система математических соотношений для объекта-системы в целом не записывается, а заменяется некоторым алгоритмом, моделирующим ее поведение и учитывающим взаимодействие друг с другом отдельных элементов системы. В качестве моделей отдельных элементов могут быть использованы как аналитические, так и численные модели.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (в зависимости от целей моделирования) ЦЕЛИ МОДЕЛИРОВАНИЯ Дескриптивные Оптимизационные Управленческие Целью дескриптивных моделей (от лат. descriptio - описание) является построение законов изменения параметров модели. Эти модели описывают зависимость выходных величин от значений входных параметров. Поэтому дескриптивные модели являются реализацией описательных и объяснительных содержательных моделей на формальном уровне моделирования. Оптимизационные модели предназначены для определения оптимальных (с точки зрения некоторого критерия) параметров моделируемого объекта или же для поиска оптимального (наилучшего) режима управления некоторым процессом. Управленческие модели применяются для принятия эффективных управленческих решений в различных областях целенаправленной деятельности человека.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ТЕХНИЧЕСКИХ ОБЪЕКТОВ ВИДЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (ММ) ТЕХНИЧЕСКИХ ОБЪЕКТОВ (ТО) По форме представления ММ По характеру отображаемых свойств ТО По степени абстрагирования По способу получения ММ По учету физических свойств ТО Инвариантные Функциональные Теоретические Динамические Алгоритмические Структурные ММ микроуровня (ММ с распределенными параметрами) Экспериментальные факторные Статические Аналитические Графические (схемные) Структурнофункциональные По способности прогнозирования результатов Детерминированные Вероятностные ММ макроуровня (ММ с сосредоточенными параметрами) Непрерывные ММ метауровня Линейные Дискретные Нелинейные

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТИПОВАЯ СХЕМА ПРОЕКТИРОВАНИЯ ТЕХНИЧЕСКОГО ОБЪЕКТА В САПР Формирование ТЗ на объект проектирования уровня Проектирование системы на уровне Генерирование варианта структуры Уровень Корректировка ТЗ С Формирование математической модели Изменение структуры И Выбор исходных значений параметров Н ОПТИМИЗАЦИЯ ПАРАМЕТРОВ АНАЛИЗ Параметры оптимальны? Технические требования выполнены? Оформление технической документации Формирование ТЗ на подсистемы объекта Уровень Нет Т Изменение управляемых параметров Структурный синтез закончен? Е Нет З Да (СТРУКТУРНАЯ ОПТИМИЗАЦИЯ) Уровень

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭТАПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ (ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ) Анализ объекта моделирования, формулировка технического задания (ТЗ) на разработку модели (содержательная постановка задачи, расчетная схема) Концептуальная и математическая постановка задачи Качественный анализ и проверка корректности модели Выбор (разработка) и обоснование выбора метода решения задачи Аналитические методы Поиск решения Прочие методы Разработка алгоритма решения и исследование его свойств, реализация алгоритма в виде компьютерной программы Проверка адекватности модели Практическое использование построенной модели

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕР: ЗАДАЧА О БАСКЕТБОЛИСТЕ (содержательная постановка задачи) Разработать математическую модель, позволяющую описать полет баскетбольного мяча, брошенного игроком в баскетбольную корзину. Модель должна позволять: вычислять положение мяча в любой момент времени; определять точность попадания мяча в корзину после броска при различных начальных параметрах. Исходные данные: масса и радиус мяча; начальные координаты, начальная скорость и угол броска мяча; координаты центра и радиус корзины.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕР: ЗАДАЧА О БАСКЕТБОЛИСТЕ (концептуальная постановка задачи) Примем следующие предположения и гипотезы: объектом моделирования является баскетбольный мяч радиуса R; движение баскетбольного мяча может быть описано в соответствии с законами классической механики Ньютона; мяч будем считать материальной точкой массой m, положение которой совпадает с центром масс мяча; движение происходит в поле сил тяжести с постоянным ускорением свободного падения g ; движение мяча происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины; пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс; параметры движения мяча: координаты (x и y) и скорость (ее проекции vx и vy). Концептуальная постановка задачи: определить закон движения материальной точки массой m под действием силы тяжести, если известны начальные координаты точки xo и yo, ее начальная скорость vo и угол бросания αo. Центр корзины имеет координаты xk и yk. Вычислить точность броска Δ=x(tk)-xk, где tk определяется из условий: tk>0, vy

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИМЕР: ЗАДАЧА О БАСКЕТБОЛИСТЕ (математическая постановка задачи) Найти зависимости x(t), y(t) и vx(t) и vy(t) из решения системы дифференциальных уравнений: при следующих начальных условиях: Вычислить параметр Δ как где tk определить из условий Аналитическое решение:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ? ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ. 1. Какое место занимает моделирование среди других методов познания окружающего мира? 2. Какие типы моделирования вы знаете? Дайте им краткую характеристику. 3. Какое содержание вкладывается в понятия модель и моделирование в научно-технических дисциплинах? 4. Какие типы моделей используются в изучаемых вами дисциплинах? В чем состоят цели моделирования? 5. Что такое математическая модель и математическое моделирование? Дайте определения, сформулируйте достоинства математических моделей и их свойства. Какие примеры математических моделей вам известны? 6. Какие классификационные признаки можно выделить, приступая к классификации математических моделей? Дайте классификацию моделей в зависимости от типа объекта моделирования. 7. В чем заключается сложность моделирования систем? Приведите пример технической системы и обоснуйте свой ответ на этом примере. 8. Какие типы математических моделей можно выделить по виду оператора модели? 9. Какие типы математических моделей можно выделить по виду параметров модели? 10. Приведите классификацию математических моделей в зависимости от методов реализации моделей. В чем достоинства и недостатки этих методов? 11. Перечислите этапы построения математической модели, дав при этом краткое описание каждого этапа. 12. Что вкладывается в понятие адекватности модели? Какие цели преследует проверка адекватности модели? Укажите причины возможной неадекватности. Как соотносятся понятия «истинности» и «адекватности» модели? Литература: , , , .