Дифференциальные уравнения высших порядков

Основная терминология дифференциальных уравнений высших порядков (ДУ ВП).

Уравнение вида , где n >1 (2)

называется дифференциальным уравнением высшего порядка, т. е. n -го порядка.

Область определения ДУ, n -го порядка есть область .

В данном курсе будут рассматриваться ДУ ВП следующих видов:

Задача Коши ДУ ВП:

Пусть дано ДУ ,
и начальные условия н/у: числа .

Требуется найти непрерывную и n раз дифференцируемую функцию
:

1)
является решением данного ДУ на , т. е.
;

2) удовлетворяет заданным, начальным условиям: .

Для ДУ второго порядка геометрическая интерпретация решения задачи заключается в следующем: ищется интегральная кривая, проходящая через точку (x 0 , y 0 ) и касающаяся прямой с угловым коэффициентом k = y 0 ́ .

Теорема существования и единственности (решения задачи Коши для ДУ (2)):

Если 1)
непрерывна (по совокупности (n +1) аргументов) в области
; 2)
непрерывны (по совокупности аргументов
) в , то ! решение задачи Коши для ДУ , удовлетворяющее заданным начальным условиям н/у: .

Область называется областью единственности ДУ.

Общее решение ДУ ВП (2) – n -параметрическая функция ,
, где
– произвольные постоянные, удовлетворяющая следующим требованиям:

1)

– решение ДУ (2) на ;

2) н/у из области единственности !
:
удовлетворяет заданным начальным условиям.

Замечание .

Соотношение вида
, неявно определяющее общее решение ДУ (2) на называется общим интегралом ДУ.

Частное решение ДУ (2) получается из его общего решения при конкретном значении .

Интегрирование ДУ ВП.

Дифференциальные уравнения высших порядков, как правило, не решаются точными аналитическими методами.

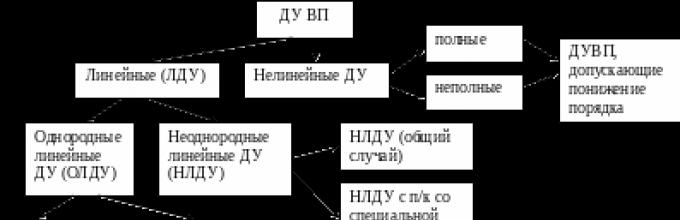
Выделим некоторого вида ДУВП, допускающих понижения порядка и сводящихся к квадратурам. Сведем в таблицу эти виды уравнений и способы понижения их порядка.

ДУ ВП, допускающие понижения порядка

Определение однородной функции:

Функция
называется однородной по переменным
, если


в любой точке области определения функции
;

– порядок однородности.

Например, – функция однородная 2-го порядка относительно
, т.е. .

Пример 1 :

Найти общее решение ДУ
.

ДУ 3-го порядка, неполное, не содержит явно
. Последовательно интегрируем уравнение три раза.

,

– общее решение ДУ.

Пример 2 :

Решить задачу Коши для ДУ
при

.

ДУ второго порядка, неполное, не содержит явно .

Подстановка
и ее производная
понизит порядок ДУ на единицу.

. Получили ДУ первого порядка – уравнение Бернулли. Для решения этого уравнения применим подстановку Бернулли:

,

и подставим в уравнение.

На этом этапе решим задачу Коши для уравнения
:
.

– уравнение первого порядка с разделяющимися переменными.

В последнее равенство подставляем начальные условия:

Ответ:
– решение задачи Коши, удовлетворяющее начальным условиям.

Пример 3:

Решить ДУ.

– ДУ 2-го порядка, неполное, не содержит явно переменную , и поэтому допускает понижение порядка на единицу с помощью подстановки или
.

Получим уравнение
(пусть
).

– ДУ 1-го порядка с разделяющими переменными. Разделим их.

– общий интеграл ДУ.

Пример 4 :

Решить ДУ.

Уравнение
есть уравнение в точных производных. Действительно,
.

Проинтегрируем левую и правую части по , т. е.
или . Получили ДУ 1-го порядка с разделяющимися переменными т. е.
– общий интеграл ДУ.

Пример5 :

Решить задачу Коши для
при .

ДУ 4-го порядка, неполное, не содержит явно
. Заметив, что это уравнение в точных производных, получим
или
,
. Подставим в это уравнение начальные условия:
. Получим ДУ
3-го порядка первого вида (см. таблицу). Проинтегрируем его три раза, и после каждого интегрирования в уравнение будем подставлять начальные условия:

Ответ:
- решение задачи Коши исходного ДУ.

Пример 6 :

Решить уравнение.

– ДУ 2-го порядка, полное, содержит однородность относительно
. Подстановка
понизит порядок уравнения. Для этого приведем уравнение к виду
, разделив обе части исходного уравнения на . И продифференцируем функцию p :

.

Подставим
и
в ДУ:
. Это уравнение 1-го порядка с разделяющимися переменными .

Учитывая, что
, получим ДУ или
– общее решение исходного ДУ.

Теория линейных дифференциальных уравнений высшего порядка.

Основная терминология.

– НЛДУ -го порядка, где – непрерывные функции на некотором промежутке .

Называется интервалом непрерывности ДУ (3).

Введем (условный) дифференциальный оператор -го порядка

При действии его на функцию , получим

Т. е. левую часть линейного ДУ -го порядка.

Вследствие этого ЛДУ можно записать

Линейные свойства оператора
:

1) – свойство аддитивности

2)
– число – свойство однородности

Свойства легко проверяются, т. к. производные этих функций обладают аналогичными свойствами (конечная сумма производных равна сумме конечного числа производных; постоянный множитель можно вынести за знак производной).

Т. о.
– линейный оператор.

Рассмотрим вопрос существования и единственности решения задачи Коши для ЛДУ
.

Разрешим ЛДУ относительно
: ,
, – интервал непрерывности.

Функция непрерывная в области , производные
непрерывны в области

Следовательно, область единственности , в которой задача Коши ЛДУ (3) имеет единственное решение и зависит только от выбора точки
, все остальные значения аргументов
функции
можно брать произвольными.

Общая теория ОЛДУ .

– интервал непрерывности.

Основные свойства решений ОЛДУ:

1. Свойство аддитивности

(
– решение ОЛДУ (4) на )
(
– решение ОЛДУ (4) на ).

Доказательство:

– решение ОЛДУ (4) на

– решение ОЛДУ (4) на

Тогда

2. Свойство однородности

( – решение ОЛДУ (4) на ) (
( – числовое поле))

– решение ОЛДУ (4) на .

Доказывается аналогично.

Свойства аддитивности и однородности называются линейными свойствами ОЛДУ (4).

Следствие:

(
– решение ОЛДУ (4) на )(

– решение ОЛДУ (4) на ).

3. ( – комплексно-значное решение ОЛДУ (4) на )(
– действительно-значные решения ОЛДУ (4) на ).

Доказательство:

Если – решение ОЛДУ (4) на , то при подстановке в уравнение обращает его в тождество, т. е.
.

В силу линейности оператора , левую часть последнего равенства можно записать так:
.

Это значит, что , т. е. – действительно-значные решения ОЛДУ (4) на .

Последующие свойства решений ОЛДУ связаны с понятием “линейная зависимость ”.

Определение линейной зависимости конечной системы функций

Система функций называется линейно зависимой на , если найдётся нетривиальный набор чисел
такой, что линейная комбинация
функций
с этими числами тождественно равна нулю на , т. е.
.n , что неверно. Теорема доказана.дифференциальные уравнения высших порядков (4 час...

Дифференциальные уравнения второго порядка и высших порядков.
Линейные ДУ второго порядка с постоянными коэффициентами.
Примеры решений.

Переходим к рассмотрению дифференциальных уравнений второго порядка и дифференциальных уравнений высших порядков. Если Вы смутно представляете, что такое дифференциальное уравнение (или вообще не понимаете, что это такое), то рекомендую начать с урока Дифференциальные уравнения первого порядка. Примеры решений . Многие принципы решения и базовые понятия диффуров первого порядка автоматически распространяются и на дифференциальные уравнения высших порядков, поэтому очень важно сначала разобраться с уравнениями первого порядка .

У многих читателей может быть предубеждение, что ДУ 2-го, 3-го и др. порядков – что-то очень трудное и недоступное для освоения. Это не так. Научиться решать диффуры высшего порядка вряд ли сложнее, чем «обычные» ДУ 1-го порядка . А местами – даже проще, поскольку в решениях активно используется материал школьной программы.

Наиболее популярны дифференциальные уравнения второго порядка . В дифференциальное уравнение второго порядка обязательно входит вторая производная и не входят

Следует отметить, что некоторые из малышей (и даже все сразу) могут отсутствовать в уравнении, важно, чтобы дома был отец . Самое примитивное дифференциальное уравнение второго порядка выглядит так:

Дифференциальные уравнения третьего порядка в практических заданиях встречаются значительно реже, по моим субъективным наблюдениям в Государственную Думу они бы набрали примерно 3-4% голосов.

В дифференциальное уравнение третьего порядка обязательно входит третья производная и не входят производные более высоких порядков:

Самое простое дифференциальное уравнение третьего порядка выглядит так: – папаша дома, все дети на прогулке.

Аналогичным образом можно определить дифференциальные уравнения 4-го, 5-го и более высоких порядков. В практических задачах такие ДУ проскакивают крайне редко, тем не менее, я постараюсь привести соответствующие примеры.

Дифференциальные уравнения высших порядков, которые предлагаются в практических задачах, можно разделить на две основные группы.

1) Первая группа – так называемые уравнения, допускающие понижение порядка . Налетайте!

2) Вторая группа – линейные уравнения высших порядков с постоянными коэффициентами . Которые мы начнем рассматривать прямо сейчас.

Линейные дифференциальные уравнения второго порядка
с постоянными коэффициентами

В теории и практике различают два типа таких уравнений – однородное уравнение и неоднородное уравнение .

Однородное ДУ второго порядка с постоянными коэффициентами имеет следующий вид:
, где и – константы (числа), а в правой части – строго ноль.

Как видите, особых сложностей с однородными уравнениями нет, главное, правильно решить квадратное уравнение .

Иногда встречаются нестандартные однородные уравнения, например уравнение в виде , где при второй производной есть некоторая константа , отличная от единицы (и, естественно, отличная от нуля). Алгоритм решения ничуть не меняется, следует невозмутимо составить характеристическое уравнение и найти его корни. Если характеристическое уравнение будет иметь два различных действительных корня, например: , то общее решение запишется по обычной схеме: .

В ряде случаев из-за опечатки в условии могут получиться «нехорошие» корни, что-нибудь вроде . Что делать, ответ придется записать так:

С «плохими» сопряженными комплексными корнями наподобие тоже никаких проблем, общее решение:

То есть, общее решение в любом случае существует . Потому что любое квадратное уравнение имеет два корня.

В заключительном параграфе, как я и обещал, коротко рассмотрим:

Линейные однородные уравнения высших порядков

Всё очень и очень похоже.

Линейное однородное уравнение третьего порядка имеет следующий вид:
, где – константы.
Для данного уравнения тоже нужно составить характеристическое уравнение и найти его корни. Характеристическое уравнение, как многие догадались, выглядит так:
, и оно в любом случае имеет ровно три корня.

Пусть, например, все корни действительны и различны: , тогда общее решение запишется следующим образом:

Если один корень действительный , а два других – сопряженные комплексные , то общее решение записываем так:

Особый случай, когда все три корня кратны (одинаковы). Рассмотрим простейшие однородное ДУ 3-го порядка с одиноким папашей: . Характеристическое уравнение имеет три совпавших нулевых корня . Общее решение записываем так:

Если характеристическое уравнение имеет, например, три кратных корня , то общее решение, соответственно, такое:

Пример 9

Решить однородное дифференциальное уравнение третьего порядка

Решение: Составим и решим характеристическое уравнение:

, – получен один действительный корень и два сопряженных комплексных корня.

Ответ: общее решение

Аналогично можно рассмотреть линейное однородное уравнение четвертого порядка с постоянными коэффициентами: , где – константы.

Уравнение вида: называется линейным дифференциальным уравнением высшего порядка, гдеa 0 ,а 1 ,…а n -функции переменной х или константы, причём a 0 ,а 1 ,…а n и f(x) считаются непрерывными.

Если a 0 =1(если
то на него можно разделить)
уравнение примет вид:

Если
уравнение неоднородное.

уравнение однородное.

Линейные однородные дифференциальные уравнения порядка n

Уравнение вида: называются линейными однородными дифференциальными уравнениями порядкаn.

Для этих уравнений справедливы следующие теоремы:

Теорема 1: Если
- решение , то сумма
- тоже решение

Доказательство: подставим сумму в

Т.к производная любого порядка от суммы равна суме производных, то можно перегруппироватся, раскрыв скобки:

т.к y 1 и y 2 – решение.

0=0(верно)
сумма тоже решение.

теорема доказана.

Теорема 2: Если y 0 -решение , то
- тоже решение.

Доказательство: Подставим
в уравнение

т.к С выносится за знак производной, то

т.к решение, 0=0(верно)
Сy 0 -тоже решение.

теорема доказана.

Следствие из Т1 и Т2: если
- решения (*)
линейеая комбинация-тоже решение (*).

Линейно независимые и линейно зависимые системы функций. Определитель Вронского и его свойства

Определение: Система функций
- называется линейно независимой, если линейная комбинациякоэффициенты
.

Определение: Систему функций
- называют линейно зависимой, еслии есть коэффициенты
.

Возьмём систему двух линейно зависимых функций
т.к
или
- условие линейной независимости двух функций.

1)
линейно независимы

2)
линейно зависимы

3)линейно зависимы

Определение: Дана система функций
- функций переменной х.

Определитель
-определитель Вронского для системы функций
.

Для системы двух функций определитель Вронского выглядит следующим образом:

Свойства определителя Вронского:

Теорема: Об общем решении линейного однородного дифференциального уравнения 2 порядка.

Если y 1 и y 2 – линейно независимые решения линейного однородного дифференциального уравнения 2 порядка, то

общее решение имеет вид:

Доказательство:
- решение по следствию из Т1 и Т2.

Если даны начальные условия то идолжны находится однозначно.

- начальные условия.

Составим систему для нахождения и. Для этого подставим начальные условия в общее решение.

определитель этой системы:
- определитель Вронского, вычисленный в точке х 0

т.к илинейно независимы
(по 2 0)

т.к определитель системы не равен 0, то система имеет единственное решение и инаходятся из системы однозначно.

Общее решение линейного однородного дифференциального уравнения порядка n

Можно показать что уравнение имеет n линейно независимых решений

Определение: n линейно независимых решений
линейного однородного дифференциального уравнения порядкаn называется фундаментальной системой решения.

Общее решение линейного однородного дифференциального уравнения порядкаn , т.е (*) – линейная комбинация фундаментальной системы решений:

Где
- фундаментальная система решения.

Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами

Это уравнения вида:
, гдеp и g – числа(*)

Определение: Уравнение
- называетсяхарактеристическим уравнением дифференциального уравнения (*) – обычное квадратное уравнение, решение которого зависит от D, возможны следующие случаи:

1)D>0
- два действительных различных решения.

2)D=0
- один действительный корень кратности 2.

3)D<0
- два комплексно сопряжённых корня.

Для каждого из этих случаев укажем фундаментальную систему решений, составленную из 2 функций и.

Будем показывать что:

1) и- ЛНЗ

2) и- решение (*)

Рассмотрим 1 случай D>0
- 2 действительных различных корня.

Х
арактеристическое уравнение:

В качестве ФСР возьмём:

а) покажем ЛНЗ

б) покажем, что - решение (*), подставим

+p
+g
=0

верное равенство

решение (*)

аналогично показывается для y 2 .

Вывод:
- ФСР (*)
общее решение

Рассмотрим 2случай: D=0
- 1 действительный корень кратности 2.

В качестве ФСР возьмём:

ЛНЗ:
ЛНЗ есть.

-решение уравнения (см. 1 случай). Покажем что
- решение.

подставим в ДУ

-решение.

Вывод: ФСР

Пример:

3 случай : D<0
- 2 комплексно сопряжённых корня.

подставим
в характ. уравнение

комплексное число равно 0, когда действительная и мнимая часть равны 0.

- будем использовать.

Покажем, что
- образуют ФСР.

А)ЛНЗ:

Б)
-решение ДУ

верное равенство
- решение ДУ.

Аналогично показывается, что тоже решение.

Вывод: ФСР:

Общее решение:

Если заданы н.у.

- то сначала находят общее решение
, его производную:
, а потом в эту систему подставляют н.у и находяти.

Н.у:

В некоторых задачах физики непосредственную связь между величинами, описывающими процесс, установить не удается. Но существует возможность получить равенство, содержащее производные исследуемых функций. Так возникают дифференциальные уравнения и потребность их решения для нахождения неизвестной функции.

Эта статья предназначена тем, кто столкнулся с задачей решения дифференциального уравнения, в котором неизвестная функция является функцией одной переменной. Теория построена так, что с нулевым представлением о дифференциальных уравнениях, вы сможете справиться со своей задачей.

Каждому виду дифференциальных уравнений поставлен в соответствие метод решения с подробными пояснениями и решениями характерных примеров и задач. Вам остается лишь определить вид дифференциального уравнения Вашей задачи, найти подобный разобранный пример и провести аналогичные действия.

Для успешного решения дифференциальных уравнений с Вашей стороны также потребуется умение находить множества первообразных (неопределенные интегралы) различных функций. При необходимости рекомендуем обращаться к разделу .

Сначала рассмотрим виды обыкновенных дифференциальных уравнений первого порядка, которые могут быть разрешены относительно производной, далее перейдем к ОДУ второго порядка, следом остановимся на уравнениях высших порядков и закончим системами дифференциальных уравнений.

Напомним, что , если y является функцией аргумента x .

Дифференциальные уравнения первого порядка.

Простейшие дифференциальные уравнения первого порядка вида .

Запишем несколько примеров таких ДУ .

Дифференциальные уравнения можно разрешить относительно производной, произведя деление обеих частей равенства на f(x) . В этом случае приходим к уравнению , которое будет эквивалентно исходному при f(x) ≠ 0 . Примерами таких ОДУ являются .

Если существуют значения аргумента x , при которых функции f(x) и g(x) одновременно обращаются в ноль, то появляются дополнительные решения. Дополнительными решениями уравнения при данных x являются любые функции, определенные для этих значений аргумента. В качестве примеров таких дифференциальных уравнений можно привести .

Дифференциальные уравнения второго порядка.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами .

ЛОДУ с постоянными коэффициентами является очень распространенным видом дифференциальных уравнений. Их решение не представляет особой сложности. Сначала отыскиваются корни характеристического уравнения . При различных p и q возможны три случая: корни характеристического уравнения могут быть действительными и различающимися , действительными и совпадающими или комплексно сопряженными . В зависимости от значений корней характеристического уравнения, записывается общее решение дифференциального уравнения как , или , или соответственно.

Для примера рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами . Корнями его характеристического уравнения являются k 1 = -3 и k 2 = 0 . Корни действительные и различные, следовательно, общее решение ЛОДУ с постоянными коэффициентами имеет вид


Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами .

Общее решение ЛНДУ второго порядка с постоянными коэффициентами y ищется в виде суммы общего решения соответствующего ЛОДУ и частного решения исходного неоднородного уравнения, то есть, . Нахождению общего решения однородного дифференциального уравнения с постоянными коэффициентами , посвящен предыдущий пункт. А частное решение определяется либо методом неопределенных коэффициентов при определенном виде функции f(x) , стоящей в правой части исходного уравнения, либо методом вариации произвольных постоянных.

В качестве примеров ЛНДУ второго порядка с постоянными коэффициентами приведем


Разобраться в теории и ознакомиться с подробными решениями примеров мы Вам предлагаем на странице линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами .

Линейные однородные дифференциальные уравнения (ЛОДУ) и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка .

Частным случаем дифференциальных уравнений этого вида являются ЛОДУ и ЛНДУ с постоянными коэффициентами.

Общее решение ЛОДУ на некотором отрезке представляется линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, .

Главная сложность заключается именно в нахождении линейно независимых частных решений дифференциального уравнения этого типа. Обычно, частные решения выбираются из следующих систем линейно независимых функций:


Однако, далеко не всегда частные решения представляются в таком виде.

Примером ЛОДУ является .

Общее решение ЛНДУ ищется в виде , где - общее решение соответствующего ЛОДУ, а - частное решение исходного дифференциального уравнения. О нахождении мы только что говорили, а можно определить, пользуясь методом вариации произвольных постоянных.

В качестве примера ЛНДУ можно привести .

Дифференциальные уравнения высших порядков.

Дифференциальные уравнения, допускающие понижение порядка.

Порядок дифференциального уравнения , которое не содержит искомой функции и ее производных до k-1 порядка, может быть понижен до n-k заменой .

В этом случае , и исходное дифференциальное уравнение сведется к . После нахождения его решения p(x) останется вернуться к замене и определить неизвестную функцию y .

Например, дифференциальное уравнение после замены станет уравнением с разделяющимися переменными , и его порядок с третьего понизится до первого.