В радиотехнике часто применяется понятие свертки двух сигналов. Так, например, сигнал на выходе четырехполюсника можно найти с помощью свертки входного сигнала и импульсной характеристики четырехполюсника. Поскольку были рассмотрены дискретные и цифровые сигналы, то определим понятие свертки для дискретных сигналов , или дискретной свертки.
Пусть имеется дискретный сигнал х Д (t) , состоящий из N отсчетов х к , и дискретный сигнал у д (Г), состоящий из N отсчетов у к, тогда дискретной сверткой этих двух сигналов называется сигнал z A (t) , для которого
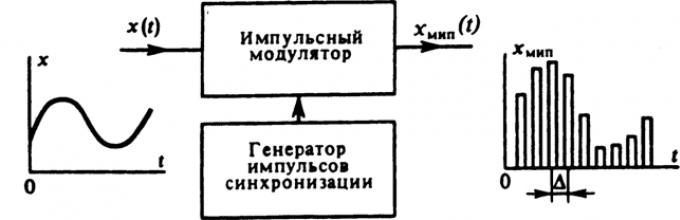
Дискретные сигналы получили широкое распространение при создании систем с импульсной модуляцией.
Устройство дискретизации в простейшем случае представляет собой стробируемый каскад (ключ), открывающийся на время т и с периодом А (рис. 4.7).

Рис. 4.
Интервал дискретизации А может быть постоянным (равномерная дискретизация) или переменным (адаптивная дискретизация). Наиболее распространенной формой дискретизации является равномерная, в основе которой лежит теорема Котельникова.
Импульсный модулятор - это устройство с двумя входами, на один из которых подается аналоговый сигнал, а на второй поступают короткие синхронизирующие импульсы с периодом повторения А. При этом в момент поступления синхроимпульса происходит измерение мгновенного значения сигнала лс(г). На выходе модулятора возникает последовательность импульсов, каждый из которых имеет площадь, пропорциональную соответствующему отсчетному значению аналогового сигнала (рис. 4.7).
Сигнал Хмпн (t ) на выходе импульсного модулятора называют модулированной импульсной последовательностью (МИП). Математически МИП записывается так
а спектральная плотность МИП выражается через спектральную плотность аналогового сигнала следующим образом:
Модель дискретного сигнала предполагает, что отсчетные значения аналогового сигнала могут быть получены в неограниченном числе точек на оси времени. Практически же обработка всегда ведется на конечном интервале времени.
Рассмотрим особенности спектрального представления дискретного сигнала, заданного на интервале своими отсчетами x 0 ,x x ,...,x N _ x . Полное число отсчетов N - Т / А.
Методика изучения таких дискретных сигналов состоит в том, что полученная выборка отсчетных значений мысленно повторяется бесконечное число раз. В результате сигнал становится периодическим (рис. 4.8).
Сопоставив такому сигналу математическую модель, можно воспользоваться разложением в ряд Фурье и найти соответствующие амплитудные коэффициенты. Совокупность этих коэффициентов образует спектр дискретного периодического сигнала.

Рис. 4.8.
Запишем модель ограниченного периодического сигнала в виде последовательности дельта-импульсов:
Разложим сигнал Хмип (0 в ряд Фурье:
здесь замена переменных? = f / А. Окончательно получаем
Эта формула определяет последовательность коэффициентов, образующих дискретное преобразование Фурье (ДПФ) рассматриваемого сигнала.
ДПФ обладает следующими свойствами:
1. ДПФ есть линейное преобразование, т. е. если z k = а х к + /? у к, то
С"Z П ~ ^ С Х п Р Су п .
2. Число различных коэффициентов Cq,Ci,...,C n _i равно числу N отсчетов за период, при n = N коэффициент C N = С 0 .
3. С 0 является средним значением всех отсчетов С 0 = - ^х к.
N к =о
- 4. Если N- четное число, то С N = -^(-1) к х к.
- 7 ^ ?=о
- 5. Если отсчеты х к - вещественные числа и N - четное число, то C N = C* N , / = 0; Л/7 2 -1.
- -+i - -i
- 6. Если y k =x k+m , m = l;JV-l,TO C, t =C, * e ~ j2rrkm,N .
- 2 tf-l
- 7. Если z k = - > T0 C z к =C X k C y k
iy/ i =0
ДПФ применяется для вычисления спектров функций, заданных таблицами или графиками, обработки экспериментальных данных, нахождения сигнала на выходе дискретного фильтра и т. д.
Если на основе отсчетов x 0 ,x l ,...,x N _ l некоторого сигнала найдены коэффициенты ДПФ C 0 ,Ci,... 9 C n/2 , то по ним можно восстановить аналоговый сигнал с ограниченным спектром x(t). Ряд Фурье такого сигнала имеет вид (при четном N)
где |Q| - модуль коэффициентов ДПФ; =arg - фазовый угол (аргумент)
коэффициентов ДПФ. Частота первой гармоники: f= - / в = - = -/i- нечетном N последнее слагаемое в формуле (4.17) равно:
Для вычисления дискретных отсчетов х к по имеющимся коэффициентам ДПФ существует следующая формула:
Эта формула носит название обратного дискретного преобразования Фурье {ОДПФ).
Преобразование Фурье (§ 1.5) можно рассматривать как линейное преобразование с ядром
Найдем его дискретное представление по базису
для сигналов с ограниченным на интервале спектром, для которых справедливо представление

Преобразование Фурье такого сигнала равно

Рассмотрим теперь периодический сигнал

Его спектр равен

где -отсчеты спектра сигнала взятого на отрезке (см. табл. 1.2, строка 19). Если Т достаточно велико, а сигнал достаточно быстро спадает до нуля на этом интервале, так что его искажениями в сумме (3.60) за счет наложения периодов можно пренебречь, то Отсюда
причем суммирование по к проводится в пределах
Значения Т и можно всегда выбрать так, чтобы величина была целой. Обозначим ее N. Обозначим также

Здесь выбрано так, чтобы суммирование в (3.62) могло производиться по к от 0 до Тогда получим

Это соотношение называется дискретным преобразованием Фурье
Дискретное преобразование Фурье обратимо:

Его ядро - матрица
![]()
является дискретным представлением ядра непрерывного преобразования Фурье.
Формула (3.65) является аналогом (3.3). Отметим, что ее можно получить сразу из (3.3) для базиса
Коэффициенты последовательности приближенно равны отсчетам спектра сигнала периодически продолженного с периодом Т, взятым с шагом Такова связь ДПФ с непрерывным преобразованием Фурье. Из предположения ограниченной протяженности сигнала вытекает, что для его спектра справедлива теорема отсчетов и что, следовательно, он может быть восстановлен по величинам - коэффициентам ДПФ отсчетов сигнала.
Наиболее употребительные свойства одномерного ДПФ приведены в табл. 3.1. Для удобства сопоставления их со свойствами непрерывного преобразования Фурье в правой колонке табл. 3.1 указаны номера соответствующих строк табл. 1.2. Главное отличие ДПФ от
(см. скан)
(см. скан)
(см. скан)
Продолжение табл. 3.1 (см. скан)
непрерывного преобразования Фурье - цикличность, или периодичность: номера отсчетов последовательности и ее ДПФ отсчитываются по модулю N, т. е. как бы по кругу; число точек в цикле равно N (табл. 3.1, строка 2).
По аналогии с одномерным ДПФ, применив двумерную теорему отсчетов к двумерным сигналам и спектрам, можно получить двумерное ДПФ. Обычно используется только такое двумерное ДПФ, которое вытекает из двумерной теоремы отсчетов в прямоугольных координатах:
Оно удобно тем, что факторизуется на два одномерных ДПФ, т. е. является разделимым.
Обратное двумерное ДПФ записывается как
Некоторые свойства двумерного ДПФ приведены в табл. 3.2. Для двумерного ДПФ характерна двумерная цикличность (периодичность). Можно считать, что коэффициенты двумерного ДПФ - это отсчеты двумерного непрерывного спектра сигнала, периодически размноженного на плоскости в прямоугольной системе координат, как на рис. 3.4, а.
Даётся программный код для прямого и обратного преобразования Фурье. Рассматривается быстрое преобразование Фурье.
Дискретное преобразование Фурье (ДПФ) - это мощный инструмент анализа, который широко используется в области цифровой обработки сигналов (ЦОС). Существуют прямое и обратное преобразования Фурье. Прямое дискретное преобразование Фурье переводит сигнал из временной области в частотную и служит для анализа частотного спектра сигнала. Обратное преобразование делает ровно противоположное: по частотному спектру сигнала восстанавливает сигнал во временной области.
Для расчёта преобразования Фурье обычно используется ускоренная процедура расчёта - т.н. быстрое преобразование Фурье (БПФ). Это позволяет в значительной мере сократить процессорное время на достаточно сложные и ресурсоёмкие математические расчёты.
1 Комплексные числа
Для начала нам потребуется вспомогательный класс, который будет описывать комплексные числа. Комплексные числа - это особый вид чисел в математике. Каждое комплексное число состоит из двух частей - действительной и мнимой. Сейчас нам достаточно знать о комплексных числах применительно к ДПФ то, что действительная часть комплексного числа хранит информацию об амплитуде сигнала, а мнимая - о фазе.
Код класса для описания комплексных чисел (разворачивается) """2 Прямое дискретное быстрое преобразование Фурье
На вход функции передаётся массив комплексных чисел. Действительная часть которого представляет произвольный дискретный сигнал, с отсчётами через равные промежутки времени. Мнимая часть содержит нули. Число отсчётов в сигнале должно равняться степени двойки. Если ваш сигнал короче, то дополните его нулями до числа, кратного степени 2: 256, 512, 1024 и т.д. Чем длиннее сигнал, тем у рассчитанного спектра будет выше разрешение по частоте.
Код для расчёта прямого быстрого преобразования Фурье на VB.NET (разворачивается) """3 Обратное дискретное быстрое преобразование Фурье
Обратное дискретное преобразование Фурье (ОДПФ) одним из этапов расчёта включает в себя прямое ДПФ на массиве комплексных чисел, где мнимая часть - это инверсия относительно оси X мнимой части спектра.
Код для расчёта обратного быстрого преобразования Фурье на VB.NET (разворачивается) """Ну и конечно же, опишем использовавшийся метод, который проверяет число элементов переданного массива:
"""
4 Проверка прямого и обратного преобразования Фурье
Теперь давайте проверим, что наши функции работают. Для этого пропустим произвольный сигнал через механизм прямого преобразования Фурье, а затем «соберём» его обратно с помощью обратного преобразования Фурье. Восстановленный сигнал должен практически совпадать с исходным. Ошибки округления, возникающие при работе с числами в компьютере, имеют место быть, поэтому сигналы не будут идентичны полностью, но их отклонение друг от друга должно быть пренебрежимо малым.
Для примера в качестве исходного сигнала возьмём функцию синуса и сформируем данные длиной 128 отсчётов вот таким образом:
Dim cn(127) As ComplexNumber For i As Integer = 0 To cn.Length - 1 cn(i) = New ComplexNumber(Math.Sin(i * 3 * Math.PI / 180)) Next
Получим вот такой сигнал:
Здесь по оси X - номера отсчётов во временной области, по оси Y - амплитуда. Обратим внимание, что сигнал состоит только из действительных частей, а мнимая часть на всём отрезке равна "0".
Теперь передадим этот сигнал на вход функции FFT(). По полученным в ходе прямого преобразования Фурье массивам комплексных чисел построим два графика - действительной (Re) и мнимой (Im) частей спектра:

Здесь по оси X - отсчёты в частотной области, по оси Y - амплитуда. Чтобы получить реальные значения частоты, необходимо рассчитать их, учитывая, что "0" оси Y соответствует нулевой частоте, максимум оси Y соответствует частоте дискретизации.
Полученный спектр сигнала передадим функции обратного преобразования Фурье IFFT(). Получим массив комплексных чисел, где действительная часть будет содержать восстановленный сигнал:

Как видно, восстановленный сигнал полностью повторяет исходный.
Линейная фильтрация изображений может осуществляться как в пространственной, так и в частотной области. При этом считается, что "низким" пространственным частотам соответствует основное содержание изображения - фон и крупноразмерные объекты, а "высоким" пространственным частотам - мелкоразмерные объекты, мелкие детали крупных форм и шумовая компонента.
Традиционно для перехода в область пространственных частот используются методы, основанные на $\textit{преобразовании Фурье}$. В последние годы все большее применение находят также методы, основанные на $\textit{вейвлет-преобразовании (wavelet-transform)}$.
Преобразование Фурье.
Преобразование Фурье позволяет представить практически любую функцию или набор данных в виде комбинации таких тригонометрических функций, как синус и косинус, что позволяет выявить периодические компоненты в данных и оценить их вклад в структуру исходных данных или форму функции. Традиционно различаются три основные формы преобразования Фурье: интегральное преобразование Фурье, ряды Фурье и дискретное преобразование Фурье.
Интегральное преобразование Фурье переводит вещественную функцию в пару вещественных функций или одну комплексную функцию в другую.
Вещественную функцию $f(x)$ можно разложить по ортогональной системе тригонометрических функций, то есть представить в виде
$$ f\left(x \right)=\int\limits_0^\infty {A\left(\omega \right)} \cos \left({2\pi \omega x} \right)d\omega -\int\limits_0^\infty {B\left(\omega \right)} \sin \left({2\pi \omega x} \right)d\omega , $$
где $A(\omega)$ и $B(\omega)$ называются интегральными косинус- и синус-преобразованиями:
$$ A\left(\omega \right)=2\int\limits_{-\infty }^{+\infty } {f\left(x \right)} \cos \left({2\pi \omega x} \right)dx; \quad B\left(\omega \right)=2\int\limits_{-\infty }^{+\infty } {f\left(x \right)} \sin \left({2\pi \omega x} \right)dx. $$
Ряд Фурье представляет периодическую функцию $f(x)$, заданную на интервале $$, в виде бесконечного ряда по синусам и косинусам. То есть периодической функции $f(x)$ ставится в соответствие бесконечная последовательность коэффициентов Фурье
$$ f\left(x \right)=\frac{A_0 }{2}+\sum\limits_{n=1}^\infty {A_n } \cos \left({\frac{2\pi xn}{b-a}} \right)+\sum\limits_{n=1}^\infty {B_n \sin \left({\frac{2\pi xn}{b-a}} \right)} , $$
$$ A_n =\frac{2}{b-a}\int\limits_a^b {f\left(x \right)} \cos \left({\frac{2\pi nx}{b-a}} \right)dx; \quad B_n =\frac{2}{b-a}\int\limits_a^b {f\left(x \right)} \sin \left({\frac{2\pi nx}{b-a}} \right)dx. $$
Дискретное преобразование Фурье переводит конечную последовательность вещественных чисел в конечную последовательность коэффициентов Фурье.
Пусть $\left\{ {x_i } \right\}, i= 0,\ldots, N-1 $ - последовательность вещественных чисел - например, отсчеты яркости пикселов по строке изображения. Эту последовательность можно представить в виде комбинации конечных сумм вида
$$ x_i =a_0 +\sum\limits_{n=1}^{N/2} {a_n } \cos \left({\frac{2\pi ni}{N}} \right)+\sum\limits_{n=1}^{N/2} {b_n \sin \left({\frac{2\pi ni}{N}} \right)} , $$
$$ a_0 =\frac{1}{N}\sum\limits_{i=0}^{N-1} {x_i } , \quad a_{N/2} =\frac{1}{N}\sum\limits_{i=0}^{N-1} {x_i } \left({-1} \right)^i, \quad a_k =\frac{2}{N}\sum\limits_{i=0}^{N-1} {x_i \cos \left({\frac{2\pi ik}{N}} \right)}, $$
$$
b_k =\frac{2}{N}\sum\limits_{i=0}^{N-1} {x_i \sin \left({\frac{2\pi ik}{N}} \right)},
\quad
i\le k Основное отличие между тремя формами преобразования Фурье заключается в том,
что если интегральное преобразование Фурье определено по всей области
определения функции $f(x)$, то ряд и дискретное преобразование Фурье
определены только на дискретном множестве точек, бесконечном для ряда Фурье
и конечном для дискретного преобразования. Как видно из определений преобразования Фурье, наибольший интерес для систем
цифровой обработки сигналов представляет дискретное преобразование Фурье.
Данные, получаемые с цифровых носителей или источников информации,
представляют собой упорядоченные наборы чисел, записанные в виде векторов
или матриц. Обычно принимается, что входные данные для дискретного преобразования
представляют собой равномерную выборку с шагом $\Delta $, при этом величина
$T=N\Delta $ называется длиной записи, или основным периодом. Основная
частота равна $1/T$. Таким образом, в дискретном преобразовании Фурье
производится разложение входных данных по частотам, которые являются целым
кратным основной частоты. Максимальная частота, определяемая размерностью
входных данных, равна $1/2 \Delta $ и называется $\it{частотой Найквиста}$. Учет частоты Найквиста
имеет важное значение при использовании дискретного преобразования. Если
входные данные имеют периодические составляющие с частотами, превышающими
частоту Найквиста, то при вычислении дискретного преобразования Фурье
произойдет подмена высокочастотных данных более низкой частотой, что может
привести к ошибкам при интерпретации результатов дискретного преобразования. Важным инструментом анализа данных является также $\it{энергетический спектр}$. Мощность сигнала на
частоте $\omega $ определяется следующим образом: $$
P \left(\omega \right)=\frac{1}{2}\left({A \left(\omega \right)^2+B \left(\omega \right)^2} \right) .
$$ Эту величину часто называют $\it{энергией сигнала}$ на частоте $\omega $. Согласно теореме
Парсеваля общая энергия входного сигнала равна сумме энергий по всем
частотам. $$
E=\sum\limits_{i=0}^{N-1} {x_i^2 } =\sum\limits_{i=0}^{N/2} {P \left({\omega _i } \right)} .
$$ График зависимости мощности от частоты называется энергетическим спектром
или спектром мощности. Энергетический спектр позволяет выявлять скрытые
периодичности входных данных и оценивать вклад определенных частотных
компонент в структуру исходных данных. Кроме тригонометрической формы записи дискретного преобразования Фурье
широко используется $\it{комплексное представление}$. Комплексная форма записи преобразования Фурье широко
используется в многомерном анализе и в частности при обработке изображений. Переход из тригонометрической в комплексную форму осуществляется на
основании формулы Эйлера $$
e^{j\omega t}=\cos \omega t+j\sin \omega t,
\quad
j=\sqrt {-1} .
$$ Если входная последовательность представляет собой $N$ комплексных чисел, то
ее дискретное преобразование Фурье будет иметь вид $$
G_m =\frac{1}{N}\sum\limits_{n=1}^{N-1} {x_n } e^{\frac{-2\pi jmn}{N}},
$$ а обратное преобразование $$
x_m =\sum\limits_{n=1}^{N-1} {G_n } e^{\frac{2\pi jmn}{N}}.
$$ Если входная последовательность представляет собой массив вещественных
чисел, то для нее существует как комплексное, так и синусно-косинусное
дискретное преобразование. Взаимосвязь этих представлений выражается
следующим образом: $$
a_0 =G_0 ,
\quad
G_k =\left({a_k -jb_k } \right)/2,
\quad
1\le k\le N/2;
$$ остальные $N/2$ значений преобразования являются комплексно сопряженными и не
несут дополнительной информации. Поэтому график спектра мощности дискретного
преобразования Фурье симметричен относительно $N/2$. Простейший способ вычисления дискретного преобразования Фурье (ДПФ) -
прямое суммирование, оно приводит к $N$ операциям на каждый коэффициент. Всего
коэффициентов $N$, так что общая сложность $O\left({N^2} \right)$. Такой
подход не представляет практического интереса, так как существуют гораздо
более эффективные способы вычисления ДПФ, называемые быстрым преобразованием
Фурье (БПФ), имеющее сложность $O (N\log N)$.
БПФ применяется только к последовательностям, имеющим длину (число
элементов), кратную степени 2. Наиболее общий принцип, заложенный в алгоритм
БПФ, заключается в разбиении входной последовательности на две
последовательности половинной длины. Первая последовательность заполняется
данными с четными номерами, а вторая - с нечетными. Это дает возможность
вычисления коэффициентов ДПФ через два преобразования размерностью $N/2$. Обозначим $\omega _m =e^{\frac{2\pi j}{m}}$, тогда $G_m =\sum\limits_{n=1}^{(N/2)-1} {x_{2n} } \omega
_{N/2}^{mn} +\sum\limits_{n=1}^{(N/2)-1} {x_{2n+1} }
\omega _{N/2}^{mn} \omega _N^m $. Для $m < N/2$ тогда можно записать $G_m =G_{\textrm{even}} \left(m \right)+G_{\textrm{odd}}
\left(m \right)\omega _N^m $. Учитывая, что элементы ДПФ с индексом
б ольшим, чем $N/2$, являются комплексно сопряженными к элементам с индексами
меньшими $N/2$, можно записать $G_{m+(N/2)} =G_{\textrm{even}} \left(m \right)-G_{\textrm{odd}}
\left(m \right)\omega _N^m $. Таким образом, можно вычислить БПФ длиной $N$,
используя два ДПФ длиной $N/2$. Полный алгоритм БПФ заключается в рекурсивном
выполнении вышеописанной процедуры, начиная с объединения одиночных элементов в пары,
затем в четверки и так до полного охвата исходного массива данных. Дискретное преобразование Фурье для двумерного массива чисел размера
$M\times N$ определяется следующим образом: $$
G_{uw} =\frac{1}{NM}\sum\limits_{n=1}^{N-1} {\sum\limits_{m=1}^{M-1} {x_{mn}
} } e^{{-2\pi j\left[ {\frac{mu}{M}+\frac{nw}{N}} \right]} },
$$ а обратное преобразование $$
x_{mn} =\sum\limits_{u=1}^{N-1} {\sum\limits_{w=1}^{M-1} {G_{uw} } }
e^{ {2\pi j\left[ {\frac{mu}{M}+\frac{nw}{N}}
\right]} }.
$$ В случае обработки изображений компоненты двумерного преобразования Фурье
называют $\textit{пространственными частотами}$. Важным свойством двумерного преобразования Фурье является возможность его
вычисления с использованием процедуры одномерного БПФ: $$
G_{uw} =\frac{1}{N}\sum\limits_{n=1}^{N-1} { \left[
{\frac{1}{M}\sum\limits_{m=0}^{M-1} {x_{mn} e^{\frac{-2\pi jmw}{M}}} } \right] } e^{\frac{-2\pi jnu}{N}},
$$ Здесь выражение в квадратных скобках есть одномерное преобразование строки
матрицы данных, которое может быть выполнено с одномерным БПФ. Таким
образом, для получения двумерного преобразования Фурье нужно сначала
вычислить одномерные преобразования строк, записать результаты в исходную
матрицу и вычислить
одномерные преобразования для столбцов полученной
матрицы. При вычислении двумерного преобразования Фурье низкие частоты будут
сосредоточены в углах матрицы, что не очень удобно для дальнейшей обработки
полученной информации. Для перевода получения представления двумерного
преобразования Фурье, в котором низкие частоты сосредоточены в центре
матрицы, можно выполнить простую процедуру, заключающуюся в умножении
исходных данных на $-1^{m+n}$. На рис. 16 показаны исходное изображение и его Фурье-образ. Полутоновое изображение и его Фурье-образ (изображения получены в системе LabVIEW) Свертка функций $s(t)$ и $r(t)$ определяется как $$
s\ast r\cong r\ast s\cong \int\limits_{-\infty }^{+\infty } {s(\tau)} r(t-\tau)d\tau .
$$ На практике приходится иметь дело с дискретной сверткой, в которой
непрерывные функции заменяются наборами значений в узлах равномерной сетки
(обычно берется целочисленная сетка): $$
(r\ast s)_j \cong \sum\limits_{k=-N}^P {s_{j-k} r_k }.
$$ Здесь $-N$ и $P$ определяют диапазон, за пределами которого $r(t) = 0$. При вычислении свертки с помощью преобразования Фурье используется свойство
преобразования Фурье, согласно которому произведение образов функций в
частотной области эквивалентно свертке этих функций во временн ой области. Для вычисления сверки необходимо преобразовать исходные данные в частотную
область, то есть вычислить их преобразование Фурье, перемножить результаты
преобразования и выполнить обратное преобразование Фурье, восстановив
исходное представление. Единственная тонкость в работе алгоритма связана с тем, что в случае
дискретного преобразования Фурье (в отличие от непрерывного) происходит
свертка двух периодических функций, то есть наши наборы значений задают
именно периоды этих функций, а не просто значения на каком-то отдельном
участке оси. То есть алгоритм считает, что за точкой $x_{N }$ идет не ноль, а
точка $x_{0}$, и так далее по кругу. Поэтому, чтобы свертка корректно
считалась, необходимо приписать к сигналу достаточно длинную
последовательность нулей. Линейные методы фильтрации относятся к числу хорошо структурированных
методов, для которых разработаны эффективные вычислительные схемы,
основанные на быстрых алгоритмах свертки и спектральном анализе. В общем
виде линейные алгоритмы фильтрации выполняют преобразование вида $$
f"(x,y) = \int\int f(\zeta -x, \eta -y)K (\zeta , \eta) d \zeta d \eta ,
$$ где $K(\zeta ,\eta)$ - ядро линейного преобразования. При дискретном представлении сигнала интеграл в данной формуле вырождается
во взвешенную сумму отсчетов исходного изображения в пределах некоторой
апертуры. При этом выбор ядра $K(\zeta ,\eta)$ в соответствии с тем или
иным критерием оптимальности может привести к ряду полезных свойств
(гауссовское сглаживание при регуляризации задачи численного
дифференцирования изображения и др.). Наиболее эффективно линейные методы обработки реализуются в частотной
области. Использование Фурье-образа изображения для выполнения операций фильтрации
обусловлено прежде всего более высокой производительностью таких операций.
Как правило, выполнение прямого и обратного двумерного преобразования Фурье
и умножение на коэффициенты Фурье-образа фильтра занимает меньше времени,
чем выполнение двумерной свертки исходного изображения. Алгоритмы фильтрации в частотной области основываются на теореме о свертке.
В двумерном случае преобразование свертки выглядит следующим образом: $$
G\left({u,v} \right)=H\left({u,v} \right)F\left({u,v} \right),
$$ где $G$ - Фурье-образ результата свертки, $H$ - Фурье-образ фильтра, а
$F$ - Фурье-образ исходного изображения. То есть в частотной области двумерная
свертка заменяется поэлементным перемножением образов исходного изображения
и соответствующего фильтра. Для выполнения свертки необходимо выполнить следующие действия. Связь между функцией фильтра в частотной и пространственной области можно
определить, используя теорему о свертке $$
\Phi \left[ {f\left({x,y} \right)\ast h(x,y)} \right]=F\left({u,v}
\right)H\left({u,v} \right),
$$ $$
\Phi \left[ {f\left({x,y} \right)h(x,y)} \right]=F\left({u,v} \right)\ast
H\left({u,v} \right).
$$ Свертка функции с импульсной функцией может быть представлена следующим
образом: $$
\sum\limits_{x=0}^M {\sum\limits_{y=0}^N {s\left({x,y} \right)}
} \delta \left({x-x_0 ,y-y_0 } \right)=s(x_0 ,y_0).
$$ Фурье-преобразование импульсной функции $$
F\left({u,v} \right)=\frac{1}{MN}\sum\limits_{x=0}^M
{\sum\limits_{y=0}^N {\delta \left({x,y} \right) } } e^{ {-2\pi
j\left({\frac{ux}{M}+\frac{vy}{N}}
\right)} }
=\frac{1}{MN}.
$$ Пусть $f(x,y) = \delta (x,y)$, тогда свертка $$
f\left({x,y} \right)\ast h(x,y)=\frac{1}{MN}h\left({x,y} \right),
$$ $$
\Phi \left[ {\delta \left({x,y} \right)\ast h(x,y)} \right]=\Phi
\left[ {\delta \left({x,y} \right)} \right]H\left({u,v}
\right)=\frac{1}{MN}H\left({u,v} \right).
$$ Из этих выражений видно, что функции фильтра в частотной и пространственной
областях взаимосвязаны через преобразование Фурье. Для данной функции
фильтра в частотной области всегда можно найти соответствующий фильтр в
пространственной области, применив обратное преобразование Фурье. То же верно
и для обратного случая. Используя данную взаимосвязь, можно определить
процедуру синтеза пространственных линейных фильтров.
{$\textit{Идеальный фильтр низких частот}$} $H(u,v)$ имеет вид
$$H(u,v) = 1, \quad \mbox{если }D(u,v) < D_0 ,$$
$$H(u,v) = 0, \quad \mbox{если }D(u,v) \ge D_0 ,$$
где $D\left({u,v} \right)=\sqrt {\left({u-\frac{M}{2}} \right)^2+\left({v-\frac{N}{2}} \right)^2}$ - расстояние от центра частотной плоскости. {$\textit{Идеальный высокочастотный фильтр}$} получается путем
инверсии идеального низкочастотного фильтра: $$
H"(u,v) = 1-H(u,v).
$$ Здесь происходит полное подавление низкочастотных компонент при сохранении
высокочастотных. Однако как и в случае идеального низкочастотного фильтра,
его применение чревато появлением существенных искажений. Для синтеза фильтров с минимальными искажениями используются различные
подходы. Одним из них является синтез фильтров на основе экспоненты. Такие
фильтры привносят минимальные искажения в результирующее изображение и
удобны для синтеза в частотной области. Широко используемым при обработке изображений является семейство фильтров на
основании вещественной функции Гаусса. $\textit{Низкочастотный гауссовский фильтр}$ имеет вид $$
h\left(x \right)=\sqrt {2\pi } \sigma Ae^{-2\left({\pi \sigma
x} \right)^2} \mbox{ и } H\left(u \right)=Ae^{-\frac{u^2}{2\sigma ^2}}
$$ Чем уже профиль фильтра в частотной области (чем больше $\sigma $), тем он
шире в пространственной. {$\textit{Высокочастотный гауссовский фильтр}$} имеет вид $$
h\left(x \right)=\sqrt {2\pi } \sigma _A Ae^{-2\left({\pi \sigma _A x}
\right)^2}-\sqrt {2\pi } \sigma _B Be^{-2\left({\pi \sigma _B x} \right)^2 },
$$ $$
H\left(u \right)=Ae^{-\frac{u^2}{2\sigma _A^2 }}-Be^{-\frac{u^2}{2\sigma
_B^2 }}.
$$ В двумерном случае {$\it{низкочастотный}$} фильтр гаусса
выглядит следующим образом: $$
H\left({u,v} \right)=e^{-\frac{D^2\left({u,v} \right)}{2D_0^2 }}.
$$ {$\it{Высокочастотный}$} гауссовский фильтр имеет вид $$
H\left({u,v} \right)=1-e^{-\frac{D^2\left({u,v} \right)}{2D_0^2 }}.
$$ Рассмотрим пример фильтрации изображения (рис. 1) в частотной области
(рис. 17 - 22). Заметим, что частотная фильтрация изображения может
иметь смысл как сглаживания ($\textit{низкочастотная фильтрация}$), так и выделения контуров и мелкоразмерных
объектов ($\textit{высокочастотная фильтрация}$). Как видно из рис. 17, 19, по мере нарастания "мощности" фильтрации в низкочастотной
составляющей изображения все сильнее проявляется эффект "кажущейся расфокусировки" или
$\it{размытия}$ изображения. В то же время в высокочастотную составляющую, где в начале
наблюдаются лишь контура объектов, постепенно переходит большая часть
информационного содержания изображения (рис. 18, 20 - 22). Рассмотрим теперь поведение высокочастотных и низкочастотных фильтров
(рис. 23 - 28)
в присутствии аддитивного гауссовского шума на изображении (рис. 7). Как видно из рис. 23, 25, свойства низкочастотных фильтров по
подавлению аддитивной случайной помехи аналогичны свойствам ранее
рассмотренных линейных фильтров - при достаточной мощности фильтра помехи
подавляются, однако платой за это является сильное размытие контуров и
"расфокусировка" всего изображения. Высокочастотная составляющая
зашумленного изображения перестает быть информативной, так как помимо
контурной и объектовой информации там теперь также полностью присутствует и
шумовая компонента (рис. 27, 28). Применение частотных методов наиболее целесообразно в случае, когда известны
статистическая модель шумового процесса или/и оптическая передаточная
функция канала передачи изображения. Учесть такие априорные данные удобно,
выбрав в качестве восстанавливающего фильтра обобщенный управляемый
(параметрами $\sigma$ и $\mu$) фильтр следующего вида: $$
F(w_1,w_2)=
\left[
{ \frac
{1}
{P(w_1,w_2)}
}\right]
\cdot
\left[
{\frac
{{\vert P(w_1,w_2) \vert }^2}
{\vert P(w_1,w_2) \vert ^2 + \alpha \vert Q(w_1,w_2) \vert ^2}
}\right].
$$ где $0 < \sigma < 1$, $0 < \mu < 1$ - назначаемые параметры фильтра,
$P(w_{1}$, $w_{2})$ - передаточная функция системы, $Q(w_{1}$, $w_{2})$ -
стабилизатор фильтра, согласованный с энергетическим спектром фона. Выбор
параметров $\sigma = 1$, $\mu = 0$ приводит к чисто инверсной фильтрации,
$\sigma =\mu = 1$ к \it{винеровской фильтрации}, что позволяет получить изображение, близкое к
истинному в смысле минимума СКО при условии, что спектры
плотности мощности
изображения и его шумовой компоненты априорно известны. Для дальнейшего
улучшения эффекта сглаживания в алгоритм линейной (винеровской) фильтрации
вводят адаптацию, основанную на оценке локальных статистик: математического
ожидания $M(P)$ и дисперсии $\sigma (P)$. Этот алгоритм эффективно фильтрует
засоренные однородные поверхности (области) фона. Однако при попадании в
скользящее окно обработки неоднородных участков фона импульсная
характеристика фильтра сужается ввиду резкого изменения локальных статистик,
и эти неоднородности (контуры, пятна) передаются практически без
расфокусировки, свойственной неадаптивным методам линейной фильтрации. К достоинствам методов линейной фильтрации следует отнести их ясный
физический смысл и простоту анализа результатов. Однако при резком ухудшении
соотношения сигнал/шум, при возможных вариантах площадного зашумления и
наличии высокоамплитудного импульсного шума линейные методы предварительной
обработки могут оказаться недостаточными. В этой ситуации значительно более
мощными оказываются нелинейные методы. Преобразование Фурье
При использовании преобразований Фурье изображение представляется в виде суммы сложных показательных функций переменных амплитуды, частоты и фазы. Преобразование Фурье играет очень важную роль во многих областях обработки изображений, включая улучшение, анализ, восстановление и сжатие. Основные определения преобразования Фурье
Если ƒ(m,n)
представляет собой функцию двух дискретных пространственных переменных m и n, тогда двумерное преобразование Фурье функции ƒ(m,n)
может быть представлено следующим выражением Переменные представляют собой угловые частоты. Таким образом, представляет собой функцию ƒ(m,n)
в частотной области. является комплекснозначной функцией с соответствующими частотами . Частоты находятся в пределах диапазона , . Отметим, что F
(0,0) представляется в виде суммы всех переменных ƒ(m,n)
. По этой причине F
(0,0) часто называют постоянной составляющей преобразования Фурье. Обратное двумерное преобразование Фурье представляется выражением Т.е. это выражение представляет ƒ(m,n)
в виде суммы бесконечного числа сложных экспоненциальных функций (синусоид) с различными частотами. Амплитуда и фаза определяют вклад частот в представление . Визуализация Фурье-преобразования
При иллюстрации Фурье-преобразования допустим, что функция ƒ(m,n)
равна 1 и представлена в виде прямоугольника. Для упрощения диаграммы, функция ƒ(m,n)
будет представляться непрерывной функцией двух дискретных переменных m
и n
. На рисунке внизу с использованием функции mesh визуализировано значения амплитуд, которые получены при Фурье-преобразовании прямоугольной функции, представленной на предыдущем рисунке. Визуализацию амплитуды еще называют визуализацией преобразований Фурье. Пик функции находится в центре и отображает значение F
(0,0), которое является суммой всех значений ƒ(m,n)
. Все остальные составляющие представляют собой распределение энергии по вертикальным и горизонтальным частотам. Другой путь визуализации Фурье-преобразования заключается в отображении значений в виде изображения. Рассмотрим примеры преобразования Фурье функций различных простых форм. Дискретное косинусное преобразование
Дискретные косинусные преобразования представляют изображение в виде суммы синусоид с различной амплитудой и частотой. Функция dct2 в приложении Image Processing Toolbox реализует двумерные дискретные косинусные преобразования изображений. Одна из особенностей дискретного преобразования Фурье состоит в том, что некоторые локальные участки изображения можно охарактеризовать небольшим количеством коэффициентов дискретного преобразования Фурье. Это свойство очень часто используется при разработке методов сжатия изображений. Например, дискретное косинусное преобразование является основой международного стандарта, который используется в алгоритме сжатия изображений с потерями JPEG. Название формата “JPEG” состоит из первых букв названия рабочей группы, которая принимала участие в разработке этого стандарта (Joint Photographic Experts Group). Двумерное дискретное косинусное преобразование матрицы A
с размерами реализуется согласно следующему выражению Значения B pq
называют коэффициентами дискретного косинусного преобразования матрицы A
. (Следует отметить, что индексы матрицы в MATLAB всегда начинаются с 1, а не с 0. Поэтому элементы матрицы, которые представлены в MATLAB как A(1,1) и B(1,1), будут соответствовать элементам A 00
и B 00
из приведенной выше формулы.) Обратное дискретное косинусное преобразование реализуется согласно выражениям Выражение обратного дискретного косинусного преобразования может интерпретироваться как представление матрицы A
с размерами в виде суммы следующих функций Эти функции называются основными (базовыми) функциями дискретного косинусного преобразования. Коэффициенты дискретного косинусного преобразования B pq
можно рассматривать как весовые при каждой базовой функции. Например, для матрицы с размером элементов существует 64 базовые функции, что продемонстрировано на изображении. Горизонтальные частоты увеличиваются слева направо, а вертикальные – сверху вниз. Матрица дискретных косинусных преобразований
Приложение Image Processing Toolbox предлагает два различных пути реализации дискретных косинусных преобразований. Первый метод реализован в функции dct2. Функция dct2 использует быстрое преобразования Фурье для ускорения вычислений. Второй метод использует матрицу дискретных косинусных преобразований, которая возвращается функцией dctmtx. Матрица преобразований T формируется согласно следующего выражения Для матрицы A
с размерами представляет собой матрицу с размерами , где каждый столбец содержит одномерное дискретное косинусное преобразование A
. Двумерное дискретное косинусное преобразование A
вычисляется как B=T*A*T’
. Обратное двумерное дискретное косинусное преобразование B
вычисляется как T’*B*T.
Дискретные косинусные преобразования и сжатие изображений
В алгоритме сжатия изображений JPEG исходное изображение разделяется на блоки с размерами или элементов. Далее для каждого блока вычисляется двумерное дискретное косинусное преобразование. Коэффициенты дискретных косинусных преобразований квантируются, кодируются и передаются. Получатель JPEG–данных декодирует коэффициенты дискретного косинусного преобразования, вычисляет обратное двумерное дискретное косинусное преобразование в каждом блоке и далее совмещает их вместе в одно изображение. Рассмотрим пример вычисления двумерных дискретных косинусных преобразований в блоках с размерами элементов исходного изображения. Далее при реконструкции изображения будем учитывать только 10 коэффициентов из каждого блока, остальные приравняем к нулю. При проведении описанных вычислений будет использоваться также матрица преобразований. I = imread("cameraman.tif");
I = im2double(I);
T = dctmtx(8);
B = blkproc(I,,"P1*x*P2",T,T");
mask = ;
B2 = blkproc(B,,"P1.*x",mask);
I2 = blkproc(B2,,"P1*x*P2",T",T);
imshow(I);
figure, imshow(I2)
На рисунке представлено два изображения – исходное и реконструированное. При реконструкции изображения использовалось только 15 % коэффициентов дискретных косинусных преобразований. Однако, следует отметить, что качество реконструированного изображения является довольно приемлемым. Для просмотра других свойств дискретного косинусного преобразования см. функцию dctdemo. Преобразования Радона
Функция radon в приложении Image Processing Toolbox вычисляет матрицу проекций изображения вдоль заданных направлений. Проекция двумерной функции f(x,y) равна интегралу вдоль указанной линии. Функция Радона представляет собой вычисление проекций изображения на оси, которые задаются углами в градусах относительно горизонтали против часовой стрелки. На рисунке показана проекция некоторой фигуры под указанным углом На рисунке внизу показаны горизонтальные и вертикальные проекции для простой двумерной функции. Проекции могут вычисляться вдоль произвольного угла theta. Встроенная в приложение Image Processing Toolbox функция radon вычисляет проекции изображения вдоль определенных направлений. Проекция двумерной функции f(x,y) на ось x’ представляет собой линейный интеграл Таким образом, оси x’ y’ задаются поворотом на угол против часовой стрелки. На изображении внизу проиллюстрировано геометрию преобразования Радона. Визуализация преобразований Радона
При проведении преобразований Радона необходимо указать исходное изображение и вектор углов theta. Radon(I,theta);
R
представляет собой матрицу, в которой каждый столбец является преобразованием Радона для одного из углов, который содержится в векторе theta. Вектор xp содержит соответствующие координаты вдоль оси x. Центральный пиксель I определяется согласно выражению floor((size(I)+1)/2). Рассмотрим, как в преобразованиях Радона вычисляются проекции. Рассмотрим проекции под углом 0° и 45°. I = zeros(100,100);
I(25:75, 25:75) = 1;
imshow(I)
Radon(I,);
figure; plot(xp,R(:,1)); title("R_{0^o} (x\prime)")
Преобразования Радона при 0° Figure; plot(xp,R(:,2)); title("R_{45^o} (x\prime)")
Преобразования Радона при большом числе углов часто отображается в виде изображения. В данном примере рассмотрено преобразования Радона для изображения в виде квадрата при диапазоне углов от 0° до 180° с дискретностью 1°. Theta = 0:180;
= radon(I,theta);
imagesc(theta,xp,R);
title("R_{\theta} (X\prime)");
xlabel("\theta (degrees)");
ylabel("X\prime");
set(gca,"XTick",0:20:180);
colormap(hot);
colorbar
Использование преобразований Радона при детектировании линий
Преобразования Радона аналогичны другим известным операциям, которые известны как преобразования Хоха. Функцию radon можно применять для детектирования прямых линий. Рассмотрим основные этапы этого процесса. Наибольший пик в матрице R
соответствует =1° и x´= -80. Из центра исходного изображения проводится линия под углом на расстояние x’. Перпендикулярно к этой линии проводится прямая, которая соответствует прямой на исходном изображении. Кроме того, на изображении присутствуют и другие линии, которые представлены в матрице R
соответствующими пиками.Комплексное представление преобразования Фурье.
Быстрое преобразование Фурье.
Двумерное преобразование Фурье.
Свертка с использованием преобразования Фурье.
Фильтрация изображений в частотной области.

Прямоугольная функция
Амплитуда изображения прямоугольной функции
Логарифмическое представление Фурье-преобразования прямоугольной функции
Примеры Фурье преобразования функций различных простых форм


64 базовые функции, которые получены для матрицы с размерами элементов


Параллельно-лучевая проекция с углом поворота theta
Горизонтальная и вертикальная проекции некоторой простой функции

Геометрия преобразования Радона

Преобразования Радона при 45°
Преобразования радона с использованием 180 проекций

Геометрия преобразования Радона при детектировании прямых линий