Что такое математика. Математические науки и их метаморфозы

Математика - одна из отраслей наук. Термин математика произошел от древнегреческого глагола manthano (я изучаю). Ясно, что он недостаточен для характеристики математики в качестве особой отрасли науки. Но, как очевидно, именно этот вопрос представляет первостепенный интерес. Чтобы приблизиться к его разрешению, целесообразно обратить внимание на те науки, которые входят в состав математики: теория категорий, топология, алгебра, теория чисел и численный анализ, геометрия, математический анализ и анализ функций, теория вероятностей, математическая статистика, исследование операций, компьютерная математика.
Приведенный список содержит всего десять наук. Разумеется, нельзя утверждать, что он исчерпывает весь перечень математических наук, но в первом приближении представляет его в достаточно полном виде.
Многое относительно природы математических наук разъясняет учет истории развития математики. В своем первоначальном античном варианте математика была представлена всего двумя науками, а именно арифметикой и геометрией. Увеличение числа математических наук стало результатом многовекового развития. Причем в этом процессе ярко проявлялись следующие четыре тенденции. Во-первых, происходило обобщение математического знания, результатом которого стало появление алгебры, топологии, а затем и теории категорий. Во-вторых, видоизменялись сами арифметика и геометрия. В ее нынешнем виде арифметика входит в состав теории чисел, которая в свою очередь стоит у истоков анализа и функционального анализа, равно как и теории вероятностей. В-третьих, возникли математические дисциплины, инициированные не столько внутри математики, сколько ее окружением. К этим наукам относятся исследование операций и компьютерная

математика. В-четвертых, выявились многочисленные связи между математическими науками. Надо полагать, что в рамках математики интернаучные связи свидетельствуют о ее единстве (сравните: алгебраическая геометрия, геометрия чисел, алгебраическая теория чисел и т.п.). Указанные тенденции позволяют представить строение современной математики следующим образом (рис. 1.1).

Рис. ,1.1. Современная математика

К нам по поводу рисунка могут быть предъявлены многие претензии (указаны, мол, далеко не все интернаучные связи, относительно скромно изображена правая ветвь рисунка и т.д.). Нам было важно дать некоторый графический образ, который представил бы направление развития математического знания в основном, без учета тех тонкостей, которые нет смысла обсуждать в самом начале исследования. В частности, подчеркнем, что алгебра является обобщением теории чисел. Сходную роль по отношению к геометрии играет топология. В свою очередь теория категорий предстает как обобщение алгебры и топологии. Воспользуемся этим обстоятельством для характеристики специфики математических наук.
Очевидно, что для реализации желания дать предельно лаконичную характеристику математических наук необходимо обратиться к самой общей теории - теории категорий. В противном случае мы рискуем заблудиться в частностях. Математическая категория - это совокупность однотипных математических объектов и отображений (морфизмов) между ними. Итак, необходимо различать класс объектов и класс морфизмов. Крайне существенно, что эти два класса не равнозначны. Дело в том, что не морфизмы каким-то образом извлекаются из объектов, а последние характеризуются посредством морфизмов. Можно выразиться так: морфизмы задают специфику (смысл) объектов. Вполне правомерно утверждать, что математика является наукой о морфизмах. Этим сказано главное. Но приведенное определение математики недостаточно, если руководствоваться негласно установленной нормой, согласно которой при определении специфики той или иной науки непременно нужно характеризовать ее объекты (индивиды). С учетом этой нормы кажется, что можно определить математику следующим образом. Математика - это наука об объектах, изучаемых с точностью до морфизмов. Но это определение уже ошибочно. Дело в том, что математика изучает именно морфизмы, все остальное выходит за область ее компетенции. Выражение «с точностью до морфизмов» предполагает, что за морфизмами есть нечто такое, от чего математики абстрагируются. Математики действительно не изучают все то, что входит в состав других наук. Им нет необходимости абстрагироваться от других наук, вроде бы как «отхватывая» от них лакомый кусочек под названием морфизмы. Математика - самостоятельная наука, а изучает она морфизмы.
Греческое слово morphe означает вид. Имея дело с отображениями, математика изучает объекты одинакового вида. Только и всего. Науки о морфизмах принято называть формальными. Определенные морфизмы изучает не только математика, но и логика. Но она имеет дело не с математическими, а логическими морфизмами. Итак, математика - это наука об особых классах морфизмов. В последующем тексте мы еще не раз вернемся к этому определению. В данном же месте лишь подчеркнем, что все математические объекты, будь то числа, фигуры, кольца, поля, тензоры, векторы, определяются посредством морфизмов.
До сих пор мы рассуждали о математике. Но предметом нашего особого интереса является философия математики. Есть ли в ней необходимость? Если да, то почему?
История развития наук показывает, что до определенной поры они развиваются без философского сопровождения. Час философии науки пробивает лишь после встречи с существенными затруднениями, например парадоксами, которые никак не удается преодолеть. Физики стали философствовать в связи с необходимостью осмыслить проблемы специальной теории относительности и квантовой механики. Философия должна способствовать преодолению затора на пути научной мысли. Объектом изучения становится сама теория. А это означает, что философия науки конституируется как метанаука. Греческая приставка meta означает, что философия науки идет за, после науки. Науку, которая является объектом метанауки, принято называть субнаукой (от лат. sub - под). Если не использовать приставки meta и sub, то наука отождествляется с субнаукой, что неправомерно. Философия математики является наукой в неменьшей степени, чем субматематика. Математика - это единство суб- и метаматематики. Философия математики является наукой о субматематике.
Обратимся к метаморфозам математики, которые в конечном счете как раз и привели к конституированию философии математики.
В III в. до н.э. Евклид изобрел аксиоматическую геометрию. Это изобретение стало рубежом между квазинаучной и научной математикой. Опора на дедукцию позволяла считать геометрические доказательства достоверными, неопровержимыми. До такого рода доказательств не доходила математика Вавилонии и Древнего Египта.
Явный математический успех древних греков вызвал к жизни клубок сложнейших проблем. Что такое точка, прямая, плоскость? Уходят ли непересекающиеся линии в бесконечность? Изобретая весьма необычные математические объекты, греки всегда стремились представить их себе в форме наглядных аналогов. Аналогом геометрической точки является тело маленьких размеров. Тут вроде бы все более или менее ясно. Но что является аналогом параллельных прямых, уходящих в безбрежную даль? На этот вопрос грекам было сложно найти ответ. Понятие математической бесконечности им было чуждо уже постольку, поскольку оно не иллюстрируемо.
Скандал по поводу геометрической бесконечности хорошо известен в связи с дебатами вокруг пятой аксиомы евклидовой геометрии, которую в наши дни связывают с возможностью проведения через точку, находящуюся вне данной прямой, только одной прямой, параллельной исходной (обе прямые должны лежать в одной плоскости). Все попытки вывести пятую аксиому евклидовой геометрии из девяти других заканчивались безрезультатно. Это обстоятельство.рано или поздно должно было навести на мысль, что через точку, находящуюся вне данной прямой, можно провести либо более чем одну, либо вообще ни одной прямой, параллельной исходной линии.
Исторически первая разновидность неевклидовой геометрии была придумана Н.И. Лобачевским (1826). Среди изобретателей неевклидовых геометрий значатся также венгр Я. Больяи и немцы К. Гаусс и

Б. Риман. Открытия геометров вызвали в стане математиков явное замешательство. К. Гаусс, опасаясь окриков коллег, вообще не опубликовал результаты своих изысканий. Почему существует несколько геометрий? Геометрия - наука о пространстве, но оно вроде бы существует в единственном экземпляре. Если одно и то же пространство описывается несколькими геометриями, то какая из них истинна? Н.И. Лобачевский, рассуждая о «воображаемой геометрии», нашел изящный выход из затруднительной ситуации: «Некоторые силы в природе следуют одной, другие своей особой геометрии...». Этот вывод во времена Н.И. Лобачевского не мог быть подтвержден экспериментально. К тому же он имеет не математический, а физический статус. Речь же должна идти о математических аргументах. Математики извлекли ведь свои выводы не из физических экспериментов. Не имея возможности опереться на данные наук о природе, математикам пришлось признать, что геометрия - конструкция чисто математическая. Наиболее последовательно эту идею защищал Г. Грассман (1844).
Создание неевклидовых геометрий, во-первых, способствовало развенчанию эмпиризма в математике. Она, мол, извлекается не из эксперимента, а является продуктом творческого концептуального воображения людей. Во-вторых, благодаря неевклидовым геометриям в математике был создан плацдарм для математического плюрализма. В-третьих, неевклидовы геометрии в яркой форме представили один из типов математического обобщения. Развитие математического познания часто связано с обобщениями. В этой связи полезно вспомнить о расширении понятия числа: натуральные - дробные - отрицательные - рациональные - иррациональные - комплексные числа.
Рассмотрим еще одну линию математического обобщения, истоки которой находятся не в геометрии, а в арифметике. Ее обобщение привело к алгебре, в которой широко используются буквенные обозначения, облегчающие анализ различных числовых систем. Так называемые алгебраические операции сходны со сложением и умножением чисел. Использование в геометрии алгебраических методов превратило ее в аналитическую геометрию. Союз арифметики, алгебры и геометрии в XVII в. кульминировал в концептах переменной (вначале говорили только о переменных величинах), функции, дифференциала, производной. Так возник математический анализ с его ядром, дифференциальным и интегральным исчислением, о достоинствах которого наслышан каждый.

Ь актуальности математического анализа мало кто сомневался, но его основания привели к острейшим разногласиям в стане математиков. Особенно острые споры разразились вокруг статуса так называемых малых зеличин (постоянно напоминала о себе и проблема бесконечности, особенно в связи с расходящимися рядами). Основатели математического анализа Г. Лейбниц и И. Ньютон считали дифференциалы то нулями, то конечными величинами. Споры о природе бесконечно малых величин шли весь XVIII в. Наконец, разгул эклектического плюрализма был прерван идеями О. Коши в двадцатых годах XIX в., которые в конце того же столетия получили дальнейшее развитие в работах Б. Больцано и особенно К. Вейерштрасса.
О. Коши прославился разработкой концепта предела (некоторая переменная в процессе ее изменения неограниченно приближается к какому-то постоянному значению). Как выяснилось, основные понятия математического анализа, в том числе непрерывность, производная, интеграл, определяются посредством концепта предела.
Теория пределов имела важнейшее значение для развития философских. вопросов математики. Во-первых, теория пределов посрамила огромную армию метафизиков, которые пытались разрешить проблемы математического анализа без вхождения в его тонкости. Во-вторых, она продемонстрировала, что сами математики порой с большим трудом находят путь к новым концептам, явно нагруженным философскими моментами. Так, работы О. Коши показали, что в математическом анализе величины являются бесконечно малыми не актуально, а потенциально. В наши дни этот вывод уточнен: надо проводить различие между актуально и потенциально существующими бесконечно малыми величинами. В-третьих, теория пределов опрокинула программу эмпиризма в Математике еще более решительно, чем евклидовы геометрии. Никакой эксперимент не позволяет продемонстрировать, каким образом та или иная переменная достигает своего предела.
. При всех ее достижениях теория пределов в том виде, в каком она существовала в XIX в., обладала и недостатками. Так, при определении предела О. Коши опирался на понятие действительного числа. Но с другой етороны, иррациональные числа, а они, как известно, являются действительными числами, понимались как пределы последовательностей рациональных чисел. Налицо логический круг.
Тесзрия пределов в известной степени справилась с трудностями, связанными со статусом бесконечно малых величин. Но ее недостатки особенно четко выявились при анализе расходящихся рядов с бесконечно большим числом членов. Выяснилось, что при доказательстве теорем в математическом анализе некритически используется понятие актуальной бесконечности. Это и другие обстоятельства укрепили немецкого математика Г. Кантора в необходимости разработать теорию не только конечных, но и бесконечных множеств.
В качестве основателя теоретико-множественного подхода Кантор добился впечатляющих успехов, в частности, разработал понятие мощности множества и доказал несчетность множества всех действительных чисел, т. е. невозможность привести его во взаимнооднозначное соответствие с множеством целых положительных чисел. Таким образом, было установлено существование бесконечных множеств, имеющих разные мощности.
Но рост влияния теории множеств на развитие математики сопровождался нежелательными неожиданностями. Введение таких, казалось бы, очевидных понятий, как «мощность множества всех множеств» сопровождалось появлением парадоксов, число которых множилось. Математики оказались в весьма затруднительном положении: их любимое дитя явно капризничало.
В данном случае нет необходимости рассматривать все парадоксы теории множеств. Обратим внимание лишь на самый знаменитый парадокс, который обнаружил Б. Рассел. Множества, не содержащие себя в качестве элемента, называются собственными. Множества, включающие себя в качестве элемента, называются несобственными. Примером собственного множества является множество (класс) звезд, которое не является звездой. А вот каталог каталогов является каталогом, следовательно, он образует несобственное множество. Пусть А- множество всех множеств, не содержащее себя в качестве своего элемента. Тогда, если Ане принадлежит А, то, по определению А, Апринадлежит А; если же Апринадлежит А, то, по определению А, А не принадлежит А.
Популярной иллюстрацией парадокса Рассела является история с деревенским брадобреем, который объявил, что он бреет всех, кто не бреет себя сам. Если он не бреет себя сам, то ему надлежит брить себя, что противоречит его объявлению. Но если он бреет себя сам, то он противоречит собственному условию: брить только тех, кто сам себя не бреет. Брадобрей находится в безвыходном положении: брея себя, как и не брея себя, он противоречит своему объявлению.
Парадокс Б. Рассела поставил под сомнение сам концепт множества, именно поэтому он был воспринят математиками крайне нервозно. Следует отметить, что парадоксы теорий множеств в существенной степени стимулировали развитие философии математики. Никогда ранее в математике не ощущалась столь остро потребность в философии.
Ситуация начала XX в. в математике по философской насыщенности напоминает положение дел в квантовой физике, сложившееся в 1920- 1930-х гг. В том и другом случае философствовать были вынуждены даже те, кто этого не желал делать.
Многочисленные пути преодоления парадоксов теории множеств в случае их концептуальной классификации можно считать относящимися по крайней мере к четырем направлениям: логицизму, формализму, интуиционизму и теоретико-множественному подходу. Сторонникам этих четырех направлений так и не удалось прийти к единству мнений. В результате математика стала плюралистичной. В данном случае речь идет не об эклектическом плюрализме, часто предшествующем стадии установления рафинированной теории, а о плюрализме, в рамках которого различие подходов неустранимо.
В качестве заключения к данному параграфу, имея в виду многовековой путь развития философии математики, выделим его важнейшие этапы. Изобретение в III в. до н.э. аксиоматического метода (геометрия Евклида). Достаточно хорошо известно, что это изобретение было подготовлено трудами древнегреческих философов от Фалеса до Аристотеля. Придание алгебре самостоятельного статуса арабскими математиками (Ал-Хорезми и др.) в IX-XI вв. Оно привело к тому, что средневековая алгебра стала обобщением арифметики. Исследования арабских алгебраистов сохраняли тесную преемственность с логическими исследованиями их философского кумира Аристотеля. Именно из его логики арабы позаимствовали традицию оперирования с буквенными обозначениями. Создание философом и математиком Р. Декартом аналитической геометрии и введение им в математику переменных величин (XVII в.). Существует тесная преемственность между философией Декарта с его пристрастием к концепции протяженной субстанции и развитым им вариантом аналитической геометрии. Изобретение Г. Лейбницем и И. Ньютоном дифференциального исчисления (XVII в.). Существует определенный параллелизм между монадологией Лейбница и его математическим анализом. Создание неевклидовых геометрий во второй четверти XIX в. Н.И. Лобачевским, Я. Болъяи, К. Гауссом и Б. Риманом. Лобачевский и Гаусс в философском обосновании своих геометрических прозрений исходили из обусловленности свойств пространства материальными взаимодействиями объектов. Эта идея восходит к работам Лейбница и Аристотеля. Разработка О. Коши концепта предела (1820-е гг.). Чисто философские истоки этого понятия можно обнаружить у Аристотеля, а также у Н. Кузанского. Создание теории актуальных бесконечных множеств (Г. Кантор и др., последняя четверть XIX в.). Ее создатель руководствовался философией Платона. Разработка логицизма как философско-математического направления (Б. Рассел и др.). Расселовский логицизм является продолжением традиций британского эмпиризма с его приверженностью к номинализму. Создание интуиционистского направления в математике (Я. Брауэр, А. Рейтинг и др.). В философском отношении математический интуитивизм восходит к идеям Декарта, Паскаля и Канга. Развитие программы формализма Д. Гильбертом. В творчестве Гильберта отчетливо просматриваются философские идеи Канта. Переход на позиции философско-математического плюрализма. В этом отношении весьма показательно творчество Г. Вейля, умело сочетавшего возможности различных математических подходов1. В наши дни вряд ли вообще возможно найти выдающегося математика, который оставался бы в пределах лишь одного философско-математического направления.
Разумеется, перечисленные выше этапы дают самое общее представление о перипетиях, приведших к развитию философии математики.

Науки отличаются друг от друга по предмету исследований в первую очередь тем, что каждая из них изучает одну из сторон действительного мира, одну или несколько тесно связанных и переходящих друг в друга форм движения объективной реальности.

Рассмотрим один из возможных вариантов классификации наук:

Естественные науки, изучающие предметы, явления и закономерности природы. Среди них различают: механику, астрономию, физику, химию, палеонтологию, биологию и другие науки.

Общественные науки, изучающие явления общественной жизни. Такими науками являются историческая наука, политическая экономия и др.

Технические науки , изучающие функционирование технических устройств и систем. Например, теория машин и механизмов, сопротивление материалов и. т. п.

Науки о познании: философия, логика, психология и др.

Раньше ученые и философы нередко считали математику естественнонаучной дисциплиной. Теперь обычно говорят, что математика является самостоятельной наукой, по степени общности расположенной между философией и естествознанием.

Математика, как и другие науки, изучает действительный, материальный мир, объекты этого мира и отношения между ними. Однако в отличие от наук о природе, исследующих различные формы движения материи (механика, физика, химия, биология и т. д.) или формы передачи информации (информатика, теория автоматов и другие разделы кибернетики), математика изучает формы и отношения материального мира, взятые в отвлечении от их содержания. Поэтому математика не изучает никакой особой формы движения материи и, следовательно, не может рассматриваться как одна из естественных наук.

Во второй половине XIX в. Ф. Энгельс дал следующее определение предмета математики: «Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира, стало быть - весьма реальный материал». При этом он указывал: «Но чтобы быть в состоянии исследовать эти формы и отношения в чистом виде, необходимо совершенно отделить их от их содержания, оставить это последнее в стороне, как нечто безразличное; таким путем мы получаем точки, лишенные измерений, линии, лишенные толщины и ширины, разные а и b , x и y , постоянные и переменные величины»

Из этих слов Энгельса вытекает, что исходные понятия математики, бывшие предметом изучения с самого зарождения математической науки, - натуральное число, величина и геометрическая фигура - заимствованы из действительного мира, являются результатами абстрагирования отдельных черт материальных объектов, а не возникли путем «чистого мышления», оторванного от реальности. В то же время, для того чтобы стать предметом математического исследования, свойства и отношения материальных объектов должны быть абстрагированы от их вещественного содержания.

Таким образом, специфика математики состоит в том, что она выделяет количественные отношения и пространственные формы, присущие всем предметам и явлениям, независимо от их вещественного содержания, абстрагирует эти отношения и формы и делает их объектом своего исследования.

Однако определение Ф. Энгельса в значительной мере отражает состояние математики во второй половине XIX в. и не учитывает те ее новые области, которые непосредственно не связаны ни с количественными отношениями, ни с геометрическими формами. Это, прежде всего, математическая логика и дисциплины, связанные с программированием для ЭВМ. Поэтому определение Ф. Энгельса нуждается в некотором уточнении. Возможно, нужно сказать, что математика имеет своим объектом изучения пространственные формы, количественные отношения и логические конструкции.

Введение

Дисциплина “Математический анализ” посвящена изучению функций одной и нескольких действительных переменных и их свойств.

  Целями изучения дисциплины являются:

1. Формирование математической культуры, системного мышления и основ естественнонаучного мировоззрения.

2. Овладение аппаратом математического анализа, необходимым для понимания и освоения других математических, общенаучных и специальных дисциплин.

  Задачи изучения дисциплины состоят в следующем:

1. Изучить логическую символику и математический язык.

2. Приобрести базовые знания о функциях одной и нескольких переменных, их

свойствах и различиях.

3. Освоить методы исследования функций и выявления особенностей их

поведения.

4. Ознакомиться с основными положениями теории пределов и производных.

5. Приобрести практические навыки вычисления пределов и производных

функций одной и нескольких переменных.

6. Научиться решать задачи на нахождение максимальных и минимальных

значений функций при отсутствии и наличии каких-либо ограничений на

множество возможных решений.

Для начала изучения дисциплины достаточно знаний математики в рамках

средней школы, при этом освоение самой дисциплины необходимо для

последующего изучения дисциплин естественнонаучного блока, в частности

«Физика», и остальных разделов высшей математики (интегралы,

дифференциальные уравнения и т.д.).

Дисциплина разделена на два семестра и четыре модуля:

Модуль 1. Элементарные функции и пределы числовых последовательностей.

Модуль 2. Пределы и непрерывность функций одной переменной.

Модуль 3. Дифференциальное исчисление функций одной переменной.

Модуль 4. Функции нескольких переменных.

Каждый модуль заканчивается рубежным контролем, который позволяет

оценить как степень освоения теоретического материала модуля, так и

полученные практические навыки решения соответствующего класса

математических задач. В течение каждого модуля слушатели дисциплины

должны выполнить модульное домашнее задание, которое позволяет отработать

навыки решения задач и подготовиться к рубежному контролю. Также после

каждого семинара выдается текущее домашнее задание по пройденному на

данном семинаре материалу.

Каждый семестр состоит из двух модулей и заканчивается экзаменом (см.

рис. 1). Первый семестр является адаптационным с пониженной учебной

нагрузкой. В этом семестре слушатели знакомятся с порядком проведения

занятий, адаптируются к системе лекция-семинар- консультация и учатся

выполнять все предусмотренные контрольные мероприятия хотя бы на

минимально удовлетворительном уровне в установленные сроки. Во втором

семестре учебная нагрузка повышается примерно в два раза и становится

равной обычной нагрузке математической дисциплины, читаемой на

инженерных факультетах.

Разделение дисциплины на два семестра позволяет выстроить структуру

лекций и семинаров таким образом, чтобы учесть наличие сурдоперевода, что

делает процесс передачи знаний трехэтапным – сначала преподаватель дает

пояснения, сурдопереводчик его переводит и только потом слушатели делают

соответствующие записи. Помимо этого, в первом адаптационном семестре

много времени выделяется на правила чтения и речевое воспроизведение

математических выражений. Это позволяет решить две проблемы: проблема

запоминания достаточно большого объема новой информации – мы значительно

проблема контроля степени усвоения и понимания материала – слушатель

должен уметь не только выписывать те или иные формулы, определения и

теоремы, но и объяснять их смысл.

Рис. 1. Структура дисциплины

(ДЗ – модульное домашнее задание, РК – рубежный контроль)

В рамках дисциплины “Математический анализ” еженедельно проводятся

следующие занятия: лекции, семинары, индивидуальные и групповые

консультации. На занятиях в обязательном порядке присутствуют

сурдопереводчики. В аудиториях имеются электронные доски и проекционное

оборудование.

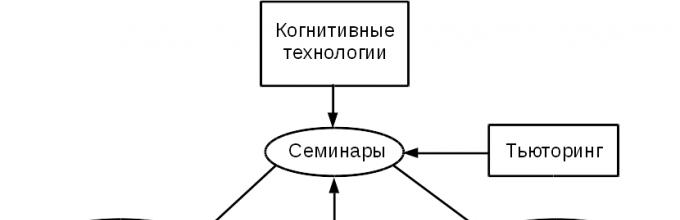
По ходу учебного процесса слушателям оказывают поддержку и

помогают преодолевать наиболее распространенные и часто встречающиеся

проблемы несколько параллельно идущих дисциплин: семантика технических

текстов, когнитивные технологии и тьюторинг. Связь “Математического

анализа” с этими дисциплинами показана на рис. 2. В рамках дисциплины

“Семантика технических текстов” выделяется несколько занятий на правильное

понимание, чтение и речевое воспроизведение наиболее часто встречающихся

на лекциях математических конструкций. “Когнитивные технологии”

актуализируют школьные знания, необходимые для успешной работы на

семинарах. В рамках тьюторинга с каждым слушателем индивидуально

отрабатываются непонятные или вызывающие трудности элементы

дисциплины.

Рис. 2. Междисциплинарные связи (овалами показаны занятия, проводимые в

рамках дисциплины “Математический анализ”, прямоугольниками – внешние дисциплины)

В разделе “Общая информация” находятся рабочая программа

дисциплины, календарные планы на оба семестра, вопросы к экзаменам,

примеры экзаменационных билетов, правила проведения экзаменов и список

лекций с краткими аннотациями. Следующие разделы “Модуль 1” - “Модуль 4”

домашнее задание. Также в этих разделах приведены тексты всех лекций и

соответствующих презентаций, использующихся на занятиях, что позволяет

слушателям либо предварительно готовиться к предстоящим занятиям, либо

восстанавливать пропущенные занятия. Последний раздел “Актуализация

знаний” содержит справочную информацию.

Элементарные функции и пределы числовых последовательностей

Рубежный контроль

Домашнее задание

Лекция 1.1

Логические символы. Виды чисел. Прямая и обратная теоремы. Необходимое и достаточное условия. Расширенное множество действительных чисел. Типы промежутков. Ограниченное и неограниченное множества. Точная верхняя и точная нижняя грани.

Лекция 1.2

Принцип вложенных отрезков. Числовая функция. Основные элементарные

функции. Элементарная функция. Числовая последовательность и ее предел.

Арифметические свойства конечных пределов.

Лекция 1.3

Необходимое и достаточное условия сходимости. Бесконечно большая

последовательность. Бесконечно малая последовательность. Теоремы о конечных

и бесконечных пределах. Число е и гиперболические функции.

Пределы и непрерывность функций одной переменной

Рубежный контроль

Домашнее задание

Лекция 2.1

Окрестность точки. Типы стремления аргумента. Предел функции в терминах

окрестностей и неравенств. Арифметические свойства пределов. Односторонние

Лекция 2.2

Общие свойства пределов. Первый замечательный предел и его следствия. Второй

замечательный предел и его следствия. Бесконечно малые функции. Бесконечно

большие функции.

Лекция 2.3

Сравнение функций. О-большое и о-малое. Эквивалентные функции и их

применение к вычислению предела. Таблица эквивалентных бесконечно малых

Лекция 2.4

Непрерывность функций. Односторонняя непрерывность. Точки разрыва и их

классификация. Свойства функций, непрерывных в точке.

Лекция 2.5

Свойства функций, непрерывных в точке (продолжение). Непрерывность функции

на промежутке. Наклонные и вертикальные асимптоты графика функции.

Дифференциальное исчисление функций одной переменной

Рубежный контроль

Домашнее задание

Лекция 3.1

Производная, ее геометрический смысл. Дифференцируемость функции. Свойства дифференцируемых функций. Дифференциал функции и его свойства.

Текст 3.1 для самостоятельного изучения

Производные основных элементарных функций. Правила нахождения производных. Приближенные вычисления с помощью дифференциала. Правила вычисления дифференциала. Производные и дифференциалы высших порядков. Физический смысл первой и второй производных.

Лекция 3.2

Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя. Порядок роста функции.

Лекция 3.3

Формула Тейлора. Формула Маклорена. Приближенные вычисления с помощью формулы Тейлора. Монотонные функции. Экстремум функции.

Текст 3.2 для самостоятельного изучения

Разложение некоторых элементарных функций по формуле Маклорена. Вычисление пределов по формуле Тейлора.

Математика - царица всех наук
Гаусс Карл Фридрих

Математика - наука, исторически основанная на решении задач о количественных и пространственных соотношениях реального мира путём идеализации необходимых для этого свойств объектов и формализации этих задач. Наука, занимающаяся изучением чисел, структур, пространств и преобразований.

Как правило, люди думают, что математика - это всего лишь арифметика, то есть изучение чисел и действий с их помощью, например, умножения и деления. На самом деле математика - это намного больше. Это способ описать мир и то, как одна его часть сочетается с другой. Взаимоотношения чисел выражаются в математических символах, которые описывают Вселенную, в которой мы живем. Любой нормальный ребенок может преуспевать в математике, потому что «ощущение числа» - это врожденная способность. Правда, для этого нужно приложить некоторые усилия и затратить немного времени.

Умение считать - это еще не все. Ребенку необходимо уметь хорошо выражать свои мысли, чтобы понимать задачи и устанавливать связи между фактами, которые хранятся в памяти. Для того чтобы выучить таблицу умножения, нужны память и речь. Именно поэтому некоторым людям с поврежденным мозгом трудно умножать, хотя другие виды счета не представляют для них сложности.

Для того чтобы хорошо знать геометрию и разбираться в форме и пространстве, требуются и другие виды мышления. С помощью математики мы решаем в жизни проблемы, например, делим шоколадку поровну или находим нужный размер ботинок. Благодаря знанию математики ребенок умеет копить карманные деньги и понимает, что можно купить и сколько денег тогда у него останется. Математика — это еще и способность отсчитать нужное количество семян и посеять их в горшочек, отмерять нужное количество муки для пирога или ткани на платье, понять счет футбольной игры и множество других повседневных дел. Везде: в банке, в магазине, дома, на работе — нам необходимо умение понимать числа, формы и меры и обращаться с ними. Числа - это только часть особого математического языка, а лучший способ выучить любой язык - это применять его. И начинать лучше с ранних лет.

О математике «умно»

Обычно идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.

Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное к математике положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика - и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе существует много различных определений математики.

Разделы математики

• Математический анализ.
• Алгебра.
• Аналитическая геометрия.
• Линейная алгебра и геометрия.
• Дискретная математика.
• Математическая логика.
• Дифференциальные уравнения.
• Дифференциальная геометрия.
• Топология.
• Функциональный анализ и интегральные уравнения.
• Теория функций комплексного переменного.
• Уравнения с частными производными.
• Теория вероятностей.
• Математическая статистика.
• Теория случайных процессов.
• Вариационное исчисление и методы оптимизации.
• Методы вычислений, то есть численные методы.
• Теория чисел.

Цели и методы

Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного математика - создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика - обеспечить достаточный набор удобных средств для достижения этой цели.

Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, - то можно абстрагироваться и от формы, оставив у модели только одну характеристику - количество. Абстракция и установление связей между объектами в самом общем виде - одно из главных направлений математического творчества.

Другое направление, наряду с абстрагированием - обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. Пространство R n , при n>3 является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях.

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.

Видео-лекция Смирнова С.К. и Ященко И.В. «Что такое математика»:

Диссертации - кандидатская и магистерская, дипломные и курсовые работы, решение задач по специальности код ВАК 01.01.00 математика

Высшая математика

Математический анализ

Дифференциальные уравнения

Математическая физика

Геометрия и топология

Теория вероятностей и математическая статистика

Математическая логика, алгебра и теория чисел

Вычислительная математика

Дискретная математика и математическая кибернетика

Математическое обеспечение вычислительных машин и систем

Системный анализ и автоматическое управление

Д иссертации - магистерская, кандидатская, НИР помощь на заказ. Консультации бесплатно!

Вы можете писать диссертацию самостоятельно или выбрать компанию, которая оказывает помощь в подготовки диссертационной работы по математике . Если у Вас еще не сформулирована тема диссертационного исследования, то на начальном этапом сотрудничества с нашей компанией являться подбор оптимальный темы для Вашей кандидатской или магистерской диссертации, научной статьи или НИР по математике

Только после согласования темы мы приступаем к подготовки плана диссертации, который необходимо согласовать с Вашим научным руководителем диссертации. Важно понимать, что в будущем формулировки плана возможно будет меняться, уточняться, но стратегия работы должна оставаться неизменной в рамках Вашего исследования, что поможет выполнить все необходимые поправки, исправления и дополнения.

При подготовки диссертации по математике на заказ происходит отдельными этапами, каждый из которых проверяется и согласовывается с Вашим научным руководителем.

Мы предлагаем Вам помощь и консультирование в написании диссертации и гарантируем ее высокое качество, актуальность и практическую значимость работы.

Каждая работа уникальна. Каждая работа пишется исключительно под заказ определенного единственного клиента.

Дипломная работа или проект по математике, алгебре, геометрии,

диплома с расчетами

На студента во время учебы возлагается не малая нагрузка, именно поэтому вы сможете воспользоваться нашей услугой, заказать помощь в подготовке дипломной работы по математике . С помощью наших специалистов вы получите уникальную и грамотно выстроенную дипломную работу по математике с учетом всех требований вашего ВУЗа и пожеланий научного руководителя. Постигать математику в ВУЗе – нелегкая задача даже для самого продвинутого студента.

Матема́тика в переводе с древнегреческого означает - изучение, наука. Это наука о структурах, порядке и отношениях, исторически сложившихся на основе операций подсчёта, измерения и описания формы предмета или объекта. Математические объекты основываются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке.

Математика не является естественной наукой, но обширно применяется в них как для точной формулировки их содержания, так и для получения новых результатов.

Математика - фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и содействует определению самых общих законов мироздания. Эта наука связана с множеством расчетов, формул, уравнениями и терминами. Постигая математику, очень сложно не заблудиться во всех этих нескончаемых цифрах и вычисления. Сложность данной науки заключается также в ее многогранности, ведь она включает в себя множество разделов:

Алгебра

Алгебра логики

Вариационная статистика и вариационное исчисление

Интегральное и дифференциальное исчисление

Теория вероятностей

Высшая математика

Дискретная математика

Теория игр

Комбинаторика

Логика высказываний

Аналитическая геометрия

Математическая логика

Математическая статистика

Матричная алгебра

Теория множеств

Традиционно математика делится:

*теоретическая, которая выполняет углублённый анализ внутриматематических структур,

*прикладная, которая предоставляет свои модели другим наукам и инженерным дисциплинам, при этом некоторые из них занимают пограничное с математикой положение.

Например, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук, а механика - и физика, и математика, так же информатику, компьютерные технологии и алгоритмика можно отнести как к инженерии, так и к математическим наукам и т. д.

Помощь в выполнении дипломной работы нашими профессиональными авторами предусматривает написание грамотной, актуальной и хорошо структурированной работы, которая будет выгодно отличаться от остальных дипломных по математике. иплом по математике , алгебре или геометрии , а так же другим математическим дисциплинам будет написан с высоким уровнем уникальности, оформлением литературных источников и практической части в соответствии с ГОСТом. Все заказанные в нашей компании материалы проходят проверку в системе «аниплагиат».

При подборе материала и выполнении дипломной работы по высшей математике наши авторы точно соблюдают сроки сдачи дипломного исследования, потому что заботятся о личном времени заказчика. Мы сами были студентами и понимаем всю волнительность данного момента! Только поэтому прежде, чем купить диплом по математике , необходимо четко и максимально ясно изложить свои требования и пожелания к дипломному проекту. Стоимость работы в нашей компании вполне демократична.

Делая заказ дипломного проекта у наших специалистов в итоге вы получите обстоятельно раскрытую тему в теоретической части, которая дополнена множеством вычислений в практической части, а в заключении сделаны правильные выводы. Готовый диплом по математике будет содержать все необходимые приложения и сопроводительные документы. Так же подготовка материала и выполнение дипломной работы на заказ по вашему требованию будет иметь речью для выступления во время защиты.

Услуги помощь в подготовки дипломных работ – наша работа, которую мы для вас выполним со всей ответственность и пониманием того, что дипломная работа решающий момент вашей жизни. Цена дипломного проекта по высшей математике вас приятно удивят, она одна из самых дешевых в Москве и России. Мечтаете об успешном окончании ВУЗа?

Оптимизируйте учебный процесс и заручитесь поддержкой профессионалов!

Сейчас на просторах интернета можно найти великое множество курсовых работ по всем дисциплинам и на множество темы. Но большое количество таких курсовых работ просто выполнено с грамматическими ошибками или оформлены не по ГОСТу, а за частую в них просто не раскрыта тема курсовой работы . Поэтому наша команда рекомендует вам заказать помощь в подготовке работы у профессиональных авторов, которые многие годы оказывают помощь в выполнении курсовые работы по алгебре , геометрии и математике на любые темы, любого объема, с обязательной проверкой в системе «антиплагиат». Вы можете абсолютно не сомневаться в том, что курсовое исследование с нашей помощью на заказ удовлетворит все требования вашего научного руководителя, и вы сможете получить высокую оценку.

Если вы решили купить помощь в выполнении курсовую работу с расчетами по следующим математическим дисциплинам: алгебра, алгебра логики, вариационная статистика и вариационное исчисление, интегральное и дифференциальное исчисление, теория вероятностей, высшая математика, дискретная математика, теория игр, комбинаторика, логика высказываний, аналитическая геометрия, математическая логика, математическая статистика, матричная алгебра, теория множеств, то вы в нужное время и в нужном месте.

Вы получите быстрый результат за доступную цену. Для того, чтобы ваша курсовая работа по геометрии , алгебре, математике получила отличную оценку, она должна касаться интересной темы. Тема также должна быть в какой-то мере уникальной. Если тема курсовой работы по математике будет редкой, тогда и работа будет сложнее писаться, но и лучше оцениваться. Вы же понимаете, что поощряется интерес студента к сложным темам. Но стоит отметить тот факт, что если купить помощь в выполнении курсовой работы на интересную и более сложную тему, придется платить немного больше обычного, но это стоит того. Ваша курсовая может стать продолжением вашего дипломного проекта. Помощь студентам – наша работа!

Решение задач по высшей математике, помощь в выполнении на заказ

Не у всех студентов и учащихся все в порядке с математикой, эта научная дисциплина очень многогранна и сложна для восприятия. Если склад ума у вас не математический, а гуманитарный, будет лучше заказать помощь в решении задач по высшей математике, что позволит высвободить время для более важных для занятий. Это могут быть самые разнообразные задания:

Интегралы

Производные

Сотрудничайте с нами - мы готовы к самым сложным заказам!