Инструкция

Неопределенность вида [∞-∞], раскрывается, если имеется в виду разность каких-либо дробей. Приведя эту разность к общему знаменателю, получите некоторое отношение функций.
Неопределенности типа 0^∞, 1^∞, ∞^0 возникают при вычислении типа p(x)^q(x). В этом случае применяют предварительное дифференцирование. Тогда искомого предела А примет вид произведения, возможно, что с готовым знаменателем. Если нет, то можно использовать методику примера 3. Главное не забыть записать окончательный ответ в виде е^А (см. рис.5).

Видео по теме
Источники:
- вычислить предел функции не пользуясь правилом лопиталя в 2019

Инструкция
Пределом называется некоторое число, к которому стремится переменная переменная или значение выражения. Обычно переменные или функции стремятся либо к нулю, либо к бесконечности. При пределе, нулю, величина считается бесконечно малой. Иными словами, бесконечно малыми называются величины, которые переменны и приближаются к нулю. Если стремится к бесконечности, то его называют бесконечным пределом. Обычно он записывается в виде:
lim x=+∞.
У есть ряд свойств, некоторые из которых представляют собой . Ниже представлены основные из них.
- одна величина имеет только один предел;
Предел постоянной величины равен величине этой постоянной;
Предел суммы равен сумме пределов: lim(x+y)=lim x + lim y;
Предел произведения равен произведению пределов: lim(xy)=lim x * lim y
Постоянный множитель может быть вынесен за знак предела: lim(Cx) = C * lim x, где C=const;
Предел частного равен частному пределов: lim(x/y)=lim x / lim y.
В задачах с пределами встречаются как числовые выражения, так и этих выражений. Это может выглядеть, в частности, следующим образом:
lim xn=a (при n→∞).
Ниже представлен несложного предела:
lim 3n +1 /n+1
n→∞.
Для решения этого предела поделите все выражение на n единиц. Известно, что если единица делится на некоторую величину n→∞, то предел 1/n равен нулю. Справедливо и обратное: если n→0, то 1/0=∞. Поделив весь пример на n, запишите его в представленном ниже виде и получите :
lim 3+1/n/1+1/n=3
При решении на пределы могут возникать результаты, которые называются неопределенностями. В таких случаях применяют правила Лопиталя. Для этого производят повторное функции, которое приведет пример в такую форму, в которой его можно было решить. Существуют два типа неопределенностей: 0/0 и ∞/∞. Пример c неопределенностью может выглядеть, в частности, следующим обращом:
lim 1-cosx/4x^2=(0/0)=lim sinx/8x=(0/0)=lim cosx/8=1/8
Видео по теме
Расчет пределов функций - фундамент математического анализа, которому посвящено немало страниц в учебниках. Однако подчас не понятно не только определение, но и сама суть предела. Говоря простым языком, предел - это приближение одной переменной величины, которая зависит от другой, к какому-то конкретному единственному значению по мере изменения этой другой величины. Для успешного вычисления достаточно держать в уме простой алгоритм решения.
Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).
Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.
Перейдём к формулировкам правил Лопиталя.
Правило Лопиталя для случая предела двух бесконечно малых величин . Если функции f (x ) и g (x a a , причём в этой окрестности g "(x a равны между собой и равны нулю
(![]() ).
).
Правило Лопиталя для случая предела двух бесконечно больших величин . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки a , за исключением, может быть, самой точки a , причём в этой окрестности g "(x )≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности
(![]() ),
),
то предел отношения этих функций равен пределу отношения их производных
(![]() ).
).
Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).
Замечания .
1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .
2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).
3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).
К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.
Раскрытие неопределённостей видов "ноль делить на ноль" и "бесконечность делить на бесконечность"
Пример 1.
![]()
x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе - производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.
Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:
Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить
Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:
Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.
Применить правило Лопиталя самостоятельно, а затем посмотреть решение
Раскрытие неопределённостей вида "ноль умножить на бесконечность"
Пример 12. Вычислить
![]() .
.
Решение. Получаем
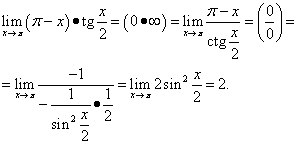
В этом примере использовано тригонометрическое тождество .
Раскрытие неопределённостей видов "ноль в степени ноль", "бесконечность в степени ноль" и "один в степени бесконечность"
Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида
Чтобы вычислить предел выражения ,
следует использовать логарифмическое тождество ,
частным случаем которого является
и свойство логарифма ![]() .
.
Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.
Пример 13.
Решение. Получаем

 .
.
![]() .
.
Пример 14. Вычислить, пользуясь правилом Лопиталя
Решение. Получаем

Вычисляем предел выражения в показателе степени
 .
.
![]() .
.
Пример 15. Вычислить, пользуясь правилом Лопиталя
Неопределённость вида и вида - самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
Большая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Неопределённость вида
Пример 1.
n равна 2. Поэтому почленно делим числитель и знаменатель на :
 .
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или "супермалому числу".
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Пример 2. .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x :
 .
.
Комментарий к ходу решения. В числителе загоняем "икс" под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо "икса".
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Неопределённость вида
Пример 3. Раскрыть неопределённость и найти предел .
Решение. В числителе - разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
В знаменателе - квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):

Запишем выражение, полученное в результате преобразований и найдём предел функции:

Пример 4. Раскрыть неопределённость и найти предел
![]()
Решение. Теорема о пределе частного здесь неприменима, поскольку
![]()
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:

Пример 5. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x
= 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Пример 6.
Вычислить ![]()
Решение: воспользуемся теоремами о пределах
Ответ: 11
Пример 7.
Вычислить ![]()
Решение: в этом примере пределы числителя и знаменателя при равны 0:
; ![]() . Получили , следовательно, теорему о пределе частного применять нельзя.
. Получили , следовательно, теорему о пределе частного применять нельзя.
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3.
Квадратный трехчлен в числителе разложим по формуле , где x 1 и х 2 – корни трехчлена. Разложив на множители и знаменатель, сократим дробь на (x-2), затем применим теорему 3.
Ответ:
Пример 8. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности, поэтому при непосредственном применении теоремы 3 получаем выражение , которое представляет собой неопределенность. Для избавления от неопределенности такого вида следует разделить числитель и знаменатель на старшую степень аргумента. В данном примере нужно разделить на х :

Ответ:
Пример 9.
Вычислить ![]()
Решение: х 3 :

Ответ: 2
Пример 10.
Вычислить ![]()
Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х 5 :
 =
= 
числитель дроби стремится к 1, знаменатель к 0, поэтому дробь стремится к бесконечности.
Ответ:
Пример 11. Вычислить
Решение: При числитель и знаменатель стремятся к бесконечности. Разделим числитель и знаменатель на старшую степень аргумента, т.е. х 7 :

Ответ: 0
Производная.
Производной функции y = f(x) по аргументу x называется предел отношения ее приращения y к приращению x аргумента x, когда приращение аргумента стремится к нулю: . Если этот предел конечен, то функция y = f(x) называется дифференцируемой в точке х. Если же этот предел есть , то говорят, что функция y = f(x) имеет в точке х бесконечную производную.
Производные основных элементарных функций:
1. (const)=0
9. ![]()
3. 11. ![]()
4. ![]() 12.
12. ![]()
5. 13. ![]()
6. ![]() 14.
14. ![]()
Правила дифференцирования:
a) ![]()
в) ![]()
Пример 1.
Найти производную функции ![]()
Решение: Если производную от второго слагаемого находим по правилу дифференцирования дроби, то первое слагаемое представляет собой сложную функцию, производная которой находится по формуле:
![]() , где
, где ![]() , тогда
, тогда

При решении были использованы формулы: 1,2,10,а,в,г.
Ответ:
Пример 21.
Найти производную функции ![]()
Решение: оба слагаемых – сложные функции, где для первого , , а для второго , , тогда
Ответ:
![]()
Приложения производной.
1. Скорость и ускорение
Пусть функция s(t) описывает положение
объекта в некоторой системе координат в момент времени t. Тогда первая производная функции s(t) является мгновенной скоростью
объекта:
v=s′=f′(t)
Вторая производная функции s(t) представляет собой мгновенное ускорение
объекта:
w=v′=s′′=f′′(t)
2. Уравнение касательной
y−y0=f′(x0)(x−x0),
где (x0,y0) − координаты точки касания, f′(x0) − значение производной функции f(x) в точке касания.

3. Уравнение нормали
y−y0=−1f′(x0)(x−x0),
где (x0,y0) − координаты точки, в которой проведена нормаль, f′(x0) − значение производной функции f(x) в данной точке.
4. Возрастание и убывание функции
Если f′(x0)>0, то функция возрастает в точке x0. На рисунке ниже функция является возрастающей при x
Если f′(x0)<0, то функция убывает в точке x0 (интервал x1

5. Локальные экстремумы функции
Функция f(x) имеет локальный максимум
в точке x1, если существует такая окрестность точки x1, что для всех x из этой окрестности выполняется неравенство f(x1)≥f(x).
Аналогично, функция f(x) имеет локальный минимум
в точке x2, если существует такая окрестность точки x2, что для всех x из этой окрестности выполняется неравенство f(x2)≤f(x).
6. Критические точки
Точка x0 является критической точкой
функции f(x), если производная f′(x0) в ней равна нулю или не существует.
7. Первый достаточный признак существования экстремума
Если функция f(x) возрастает (f′(x)>0) для всех x в некотором интервале (a,x1] и убывает (f′(x)<0) для всех x в интервале и возрастает (f′(x)>0) для всех x из интервала }









