Цели урока:
Учебные: Повторить теоретические сведения по теме «Применение производной» обобщить, закрепить и улучшить знания по данной теме.
Научить применять полученные теоретические знания при решении различного типа математических задач.
Рассмотреть методы решения заданий ЕГЭ, связанные с понятием производной базового и повышенного уровня сложности.
Воспитательные:
Обучение навыкам: планирование деятельности,работы в оптимальном темпе,работы в группе, подведение итогов.
Развивать умение оценивать свои способности,умение контактировать с товарищами.
Воспитывать чувства ответственности и сопереживания.Способствовать воспитанию умения работать в команде; умения.. относится к мнению одноклассников.
Развивающие: Уметь оформлять ключевые понятия изучаемой темы. Развивать навыки работы в группе.
Тип урока: комбинированный:
Обобщение,закрепление навыков применение свойств элементарных функций,применение уже сформированных знаний, умений и навыков применение производной в нестандартных ситуациях.
Оборудования: компьютер,проектор,экран,раздаточный материал.
План урока:
1. Организационная деятельность
Рефлексия настроения
2. Актуализация знаний учащегося
3. Устная работа
4. Самостоятельная работа в группах
5. Защита выполненных работ
6. Самостоятельная работа
7. Домашние задание
8. Итог урока
9. Рефлексия настроения
Ход урока
1. Рефлексия настроения.
Ребята,доброе утро.Я пришла к вам на урок вот с таким настроением (показываю изображение солнца)!
А какое у вас настроение?
У вас на столе лежат карточки с изображениями солнца,солнце за тучей и тучи.Покажите какое у вас настроение.
2. Анализируя результаты пробных экзаменов,а так же результаты итоговой аттестации последних лет,можно сделать вывод о том,что с заданиями математического анализа,из работы ЕГЭ справляются не более 30%-35% выпускников.Вот и в нашем классе по результатам тренировочных и диагностических работ верно выполняют их не все. Этим и обусловлен наш выбор.Будем отрабатывать навык применения производной при решении задач ЕГЭ.
Помимо проблем итоговой аттестации возникают вопросы и сомнения,в какой мере приобретаемые в этой области знания могут и будут востребованы дальнейшем,насколько оправданы как затраты времени,так и здоровья на изучение этой темы.
Зачем нужна производная? Где мы встречаемся с производной и используем ее? Можно ли без нее обойтись в математике и не только?
Сообщение ученицы 3 минуты -
3. Устная работа.
4. Самостоятельная работа в группах (3 группы)
Задание 1 группы
) В чем заключается геометрический смысл производной?
2) а) На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
б) На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

Ответ 1 группы:
1) Значение производной функции в точке x=x0 равно условному коэффициэнту касательной,проведенной к графику этой функции в точке с абсциссой х0.Нулевой коэффициент равен тангенсу угла наклона касательной (или, другими словами) тангенсу угла образованного касательной и.. направлением оси Оx)
2) А)f1(x)=4/2=2
3) Б)f1(x)=-4/2=-2
Задание 2 группы
1) В чем заключается физический смысл производной?
2) Материальная точка движется прямолинейно по закону
x(t)=-t2+8t-21, где х - расстояние от точки отсчета в метрах, t -время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=3 с.
3) Материальная точка движется прямолинейно по закону
x(t)= ½*t2-t-4, где х - расстояние от точки отсчета в метрах, t- время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Ответ 2 группы:
1) Физический (механический) смысл производной состоит в следующем.
Если S(t) закон прямоленейного движения тела,то производная выражает мгновенную скорость в момент времени t:
V(t)=-x(t)=-2t=8=-2*3+8=2
3) X(t)=1/2t^2-t-4
Задание 3 группы
1) Прямая y= 3x-5 параллельна касательной к графику функции y=x2+2x-7. Найдите абсциссу точки касания.
2) На рисунке изображен график функции y=f(x), определенной на интервале (-9;8). Определите количество целых точек на этом интервале, в которых производная функции f(x) положительна.

Ответ 3 группы:
1) Т.к прямая y=3x-5 паралельна касательной то угловой коэффициент касательной равен угловому коэффициенту прямойy=3x-5,т.е, k=3.
Y1(x)=3 ,y1=(x^2+2x-7)1=2x=2 2x+2=3
2) Целые точки -это точки с целочисленными значениями абсцисс.
Производная функция f(x) положительна,если функция возрастает.
Вопрос:Что вы можете сказать о производной функции,которую описывает поговорка «Чем дальше в лес,тем больше дров»
Ответ: Производная положительна на всей области определения,т.к эта функция - монотонно возрастает
6. Самостоятельная работа (на 6 вариантов)
7. Домашнее задание.
Тренировочная работа Ответы:
Итог урока.
«Музыка может возвышать или умиротворять душу, живопись - радовать глаз, поэзия - пробуждать чувства, философия - удовлетворять потребности разума, инженерное дело - совершенствовать материальную сторону жизни людей. Но математика способна достичь всех этих целей.»
Так сказал американский математик Морис Клайн.
Спасибо за работу!
Для начала попробуй найти область определения функции:
Справился? Сравним ответы:
Все верно? Молодец!
Теперь попробуем найти область значений функции:

Нашел? Сравниваем:
Сошлось? Молодец!
Еще раз поработаем с графиками, только теперь чуть-чуть посложнее - найти и область определения функции, и область значений функции.
Как найти и область определения и область значений функции (продвинутый вариант)

Вот что получилось:
С графиками, я думаю, ты разобрался. Теперь попробуем в соответствии с формулами найти область определения функции (если ты не знаешь как это сделать, прочитай раздел про ):
Справился? Сверим ответы :
- , так как подкоренное выражение должно быть больше или равно нулю.
- , так как на ноль делить нельзя и подкоренное выражение не может быть отрицательным.
- , так как, соответственно при всех.
- , так как на ноль делить нельзя.
Однако, у нас остался еще один не разобранный момент…
Еще раз повторю определение и сделаю на нем акцент:
Заметил? Слово «единственный» - это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.
Допустим, у нас есть функция, заданная прямой. . При, мы подставляем данное значение в наше «правило» и получаем, что. Одному значению соответствует одно значение. Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.
«Смотри! - скажешь ты, -« » встречается два раза!» Так быть может парабола не является функцией? Нет, является!
То, что « » встречается два раза далеко не повод обвинять параболу в неоднозначности!
Дело в том, что, при расчёте для, мы получили один игрек. И при расчёте с мы получили один игрек. Так что все верно, парабола является функцией. Посмотри на график:

Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!
Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:

Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» - нескольким разным икс соответствует один и тот же игрек.
Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:

Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу множества ставится в соответствие несколько элементов множества. Соответственно, это не функция.
Проверим твои знания на практике.
Определи по рисункам, что является функцией, а что нет:

Разобрался? А вот и ответы :
- Функцией является - В,Е.
- Функцией не является - А, Б, Г, Д.
Ты спросишь почему? Да вот почему:

На всех рисунках кроме В) и Е) на один приходится несколько!
Уверена, теперь, ты с легкостью отличишь функцию от не функции, скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции. Приступаем к следующему разделу - как задать функцию?
Способы задания функции
Как ты думаешь, что означают слова «задать функцию» ? Правильно, это значит объяснить всем желающим, о какой функции в данном случае идет речь. Причем объяснить так, чтобы каждый понял тебя правильно и нарисованные людьми по твоему объяснению графики функций были одинаковы.
Как это можно сделать? Как задать функцию? Самый простой способ, который уже не раз применялся в этой статье - с помощью формулы. Мы пишем формулу, и, подставляя в нее значение, высчитываем значение. А как ты помнишь, формула - это закон, правило, по которому нам и другому человеку становится ясно, как икс превращается в игрек.
Обычно, именно так и делают - в заданиях мы видим уже готовые функции, заданные формулами, однако, существуют и другие способы задать функцию, про которые все забывают, в связи с чем вопрос «как еще можно задать функцию?» ставит в тупик. Разберемся во всем по порядку, а начнем с аналитического способа.
Аналитический способ задания функции
Аналитический способ это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ. Если у тебя есть формула, то ты знаешь о функции абсолютно все - ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.
Рассмотрим функцию. Чему равно?
«Что это значит?» - спросишь ты. Сейчас объясню.
Напомню, что в записи выражение в скобках называется аргументом. И этот аргумент может быть любым выражением, не обязательно просто. Соответственно, каким бы ни был аргумент (выражение в скобках), мы его запишем вместо в выражении.
В нашем примере получится так:
Рассмотрим еще задание, связанное с аналитическим способом задания функции, которое будет у тебя на экзамене.
Найдите значение выражения, при.
Уверена, что сначала, ты испугался, увидев такое выражение, но в нем нет абсолютно ничего страшного!
Все как и в прошлом примере: каким бы ни был аргумент (выражение в скобках), мы его запишем вместо в выражении. Например, для функции.
Что же нужно сделать в нашем примере? Вместо надо написать, а вместо - :
сократить получившееся выражение:
Вот и все!
Самостоятельная работа
Теперь попробуй самостоятельно найти значение следующих выражений:
- , если
- , если
Справился? Сравним наши ответы: Мы привыкли, что функция имеет вид
Даже в наших примерах мы задаем функцию именно таким образом, однако аналитически можно задать функцию в неявном виде, например.
Попробуй построить эту функцию самостоятельно.
Справился?
Вот как строила ее я.
Какое уравнение мы в итоге вывели?
Правильно! Линейное, а это значит, что графиком будет прямая линия. Сделаем табличку, чтобы определить, какие точки принадлежат нашей прямой:
Вот как раз то, о чем мы говорили… Одному соответствует несколько.
Попробуем нарисовать то, что получилось:

Является ли то, что у нас получилось функцией?
Правильно, нет! Почему? Попробуй ответить на этот вопрос с помощью рисунка. Что у тебя вышло?

«Потому что одному значению соответствует несколько значений!»
Какой вывод мы можем из этого сделать?
Правильно, функция не всегда может быть выражена явно, и не всегда то, что «замаскировано» под функцию является функцией!
Табличный способ задания функции
Как следует из названия, этот способ представляет собой простую табличку. Да, да. Наподобие той, которой мы с тобой уже составляли. Например:
Здесь ты сразу подметил закономерность - игрек в три раза больше чем икс. А теперь задание на «очень хорошо подумать»: как ты считаешь, равносильная ли функция, заданная в виде таблицы, функции?
Не будем долго рассуждать, а будем рисовать!
Итак. Рисуем функцию, заданную обоями способами:

Видишь разницу? Дело совсем не в отмеченных точках! Присмотрись внимательнее:

Теперь увидел? Когда мы задаем функцию табличным способом, мы на графике отражаем только те точки, которые есть у нас в таблице и линия (как в нашем случае) проходит только через них. Когда мы задаем функцию аналитическим способом, мы можем взять любые точки, и наша функция ими не ограничивается. Вот такая вот особенность. Запоминай!
Графический способ построения функции
Графический способ построения функции не менее удобен. Мы рисуем нашу функцию, а другой заинтересованный человек может найти чему равен игрек при определенном икс и так далее. Графический и аналитический способы одни из самых распространенных.
Однако, здесь нужно помнить о чем мы с тобой говорили в самом начале - не каждая «загогулина» нарисованная в системе координат является функцией! Вспомнил? На всякий случай скопирую тебе сюда определение, что функцией является:
Как правило, люди обычно называют именно те три способа задания функции, которые мы разобрали - аналитический (с помощью формулы), табличный и графический, напрочь забывая о том, что функцию можно словесно описать. Как это? Да очень просто!
Словесное описание функции
Как же описать функцию словесно? Возьмем наш недавний пример - . Данную функцию можно описать «каждому действительному значению икс соответствует его утроенное значение». Вот и все. Ничего сложного. Ты, конечно, возразишь - «есть настолько сложные функции, которые словесно задать просто невозможно!» Да, есть и такие, но есть функции, которые описать словесно легче, чем задать формулой. Например: «каждому натуральному значению икс соответствует разница между цифрами, из которых он состоит, при этом за уменьшаемое берется наибольшее цифра, содержащиеся в записи числа». Теперь рассмотрим, как наше словесное описание функции реализуется на практике:
Наибольшая цифра в данном числе - , соответственно, - уменьшаемое, тогда:
Основные виды функций
Теперь перейдем к самому интересному - рассмотрим основные виды функций, с которыми ты работал/работаешь и будешь работать в курсе школьной и институтской математики, то есть познакомимся с ними, так сказать и дадим им краткую характеристику. Более подробно про каждую функцию читай в соответствующем разделе.
Линейная функция
Функция вида, где, - действительные числа.
Графиком данной функции служит прямая, поэтому построение линейной функции сводится к нахождению координат двух точек.
Положение прямой на координатной плоскости зависит от углового коэффициента.

Область определения функции (aka область допустимых значений аргумента) - .
Область значений - .
Квадратичная функция
Функция вида, где
Графиком функции является парабола, при ветви параболы направлены вниз, при — вверх.
Многие свойства квадратичной функции зависят от значения дискриминанта. Дискриминант вычисляется по формуле
Положение параболы на координатной плоскости относительно значения и коэффициента показаны на рисунке:

Область определения
Область значений зависит от экстремума данной функции (точки вершины параболы) и коэффициента (направления ветвей параболы)
Обратная пропорциональность
Функция, задаваемая формулой, где
Число называется коэффициентом обратной пропорциональности. В зависимости от того, какое значение, ветви гиперболы находятся в разных квадратах:

Область определения - .
Область значений - .
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
1. Функцией называется правило, по которому каждому элементу множества ставится в соответствие единственный элемент множества.
- - это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
- - переменная величина, или, аргумент;
- - зависимая величина - изменяется при изменении аргумента, то есть согласно какой-либо определенной формуле, отражающей зависимость одной величины от другой.
2. Допустимые значения аргумента , или область определения функции - это то, что связано с возможными, при которых функция имеет смысл.
3. Область значений функции - это то, какие значения принимает, при допустимых значениях.
4. Существует 4 способа задания функции:
- аналитический (с помощью формул);
- табличный;
- графический
- словесное описание.
5. Основные виды функций:
- : , где, - действительные числа;
- : , где;
- : , где.
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
$f"(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$
Дифференцированием называют операцию нахождения производной.
Таблица производных некоторых элементарных функций
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n$ | $nx^{n-1}$ |
| ${1}/{x}$ | $-{1}/{x^2}$ |
| $√x$ | ${1}/{2√x}$ |
| $e^x$ | $e^x$ |
| $lnx$ | ${1}/{x}$ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | ${1}/{cos^2x}$ |
| $ctgx$ | $-{1}/{sin^2x}$ |
Основные правила дифференцирования
1. Производная суммы (разности) равна сумме (разности) производных
$(f(x) ± g(x))"= f"(x)±g"(x)$
Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$
Производная суммы (разности) равна сумме (разности) производных.
$f"(x) = (3x^5)"-(cos x)" + ({1}/{x})" = 15x^4 + sinx - {1}/{x^2}$
2. Производная произведения
$(f(x) · g(x))"= f"(x) · g(x)+ f(x) · g(x)"$
Найти производную $f(x)=4x·cosx$
$f"(x)=(4x)"·cosx+4x·(cosx)"=4·cosx-4x·sinx$
3. Производная частного
$({f(x)}/{g(x)})"={f"(x)·g(x)-f(x)·g(x)"}/{g^2(x)}$
Найти производную $f(x)={5x^5}/{e^x}$
$f"(x)={(5x^5)"·e^x-5x^5·(e^x)"}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$
4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))"=f"(g(x))·g"(x)$
$f"(x)=cos"(5x)·(5x)"=-sin(5x)·5= -5sin(5x)$
Физический смысл производной
Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.
Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ - координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x"(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
Следовательно, можем составить общее равенство:
$f"(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f"(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f"(x_0) = tg α = 0$. Точка $x_0$, в которой $f "(x_0) = 0$, называется экстремумом .
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Касательная к графику возрастает, следовательно, $f"(x_0) = tg α > 0$
Для того, чтобы найти $f"(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$
$f"(x_0) = tg ВАС = 0,25$
Ответ: $0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f"(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
Если $f"(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.
В ответ запишите количество данных точек.
В задании №13 ЕГЭ по математике базового уровня придется продемонстрировать умения и знания одного из понятий поведения функции: производных в точке или скоростей возрастания или убывания. Теория к этому заданию будет добавлена чуть позже, но это не помешает нам подробно разобрать несколько типовых вариантов.
Разбор типовых вариантов заданий №14 ЕГЭ по математике базового уровня
Вариант 14МБ1
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.

Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
В таблице под каждой буквой укажите соответствующий номер.
Алгоритм выполнения:
- Выбрать интервал времени, на котором температура падала.
- Приложить линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
Решение:
Выберем интервал времени, на котором температура падала. Этот участок видно не вооруженным глазом, он начинается в 8 мин от момента запуска двигателя.
Приложим линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.

Ниже линейки окажется участок, соответствующий интервалу времени 0 – 1 мин.
С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
Опустим из точек, соответствующих 40°С и 80°С перпендикуляры на график, а из полученных точек опустим перпендикуляры на ось времени.

Видим, что этому температурному интервалу соответствует интервал времени 3 – 6,5 мин. То есть из приведенных в условии 3 – 6 мин.
Методом исключения выберем недостающий вариант ответа.
Вариант 14МБ2
Решение:
Проанализируем график функции А. Если Функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. В точке максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 3.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 4. Точка максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Сначала функция В возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. Точка максимума функции x = 1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 1.
Ответ: 3421.
Вариант 14МБ3
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А.
Если функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 3 и 4. В точке максимума функции x=0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x=-1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Проанализируем график функции В.
Сначала функция В убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x = 0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 1.
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 3.
Ответ: 4213.
Вариант 14МБ4
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

ТОЧКИ
А
В
С
D
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) –4
2) 3
3) 2/3
4) -1/2
Вспомним, что означает производная, а именно ее значение в точке — значение функции производной в точке равно тангенсу угла наклона (коэффициенту) касательной.
В ответах у нас есть два положительных, и два отрицательных варианта. Как мы помним, если коэффициент прямой (графика y = kx+ b ) положительный — то прямая возрастает, если же он отрицательный — то прямая убывает.
Возрастающих прямых у нас две — в точке A и D. Теперь вспомним, что же означает значение коэффициента k?
Коэффициент k показывает, насколько быстро возрастает или убывает функция (на самом деле коэффициент k сам является производной функции y = kx+ b).
Поэтому k = 2/3 соответствует более пологой прямой — D, а k = 3 — A.
Аналогично и в случае с отрицательными значениями: точке B соответствует более крутая прямая с k = — 4, а точке С — -1/2.
Вариант 14МБ5
На рисунке точками показаны объемы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей .

Алгоритм выполнения
Анализируем части графика, соответствующие разным временам года. Формулируем ситуации, отображенные на графике. Находим для них наиболее подходящие варианты ответов.
Решение:
Зимой кол-во продаж превысило 120 шт./мес., причем оно все время увеличивалось. Эта ситуация соответствует варианту ответа №3. Т.е. получаем: А–3 .
Весной продажи постепенно упали со 120 обогревателей за месяц до 50. Наиболее приближенным к этой формулировке является вариант №2. Имеем: Б–2 .
Летом кол-во продаж не менялась и была минимальной. 2-я часть этой формулировки не отражена в ответах, а для первой подходит только №4. Отсюда имеем: В–4 .
Осенью продажи росли, однако их кол-во ни в одном из месяцев не превысило 100 штук. Эта ситуация описана в варианте №1. Получаем: Г–1 .
Вариант 14МБ6
На графике изображена зависимость скорости движения рейсового автобуса от времени. На вертикальной оси отмечена скорость автобуса в км/ч, на горизонтальной – время в минутах, прошедшее с начала движения автобуса.
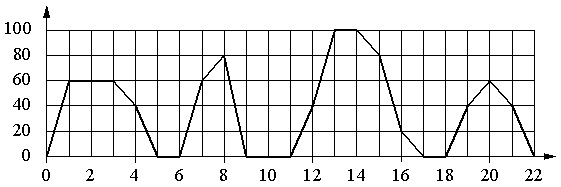
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.

Алгоритм выполнения
- Определяем цену деления на горизонтальной и на вертикальной шкале.
- Анализируем по очереди предложенные утверждения 1–4 из правой колонки («Характеристики»). Сопоставляем их с временными интервалами из левой колонки таблицы, находим пары «буква–число» для ответа.
Решение:
Цена деления горизонтальной шкалы составляет 1 с, вертикальной – 20 км/ч.
- Когда автобус делает остановку, его скорость равна 0. Нулевую скорость в течение 2 минут подряд автобус имел только с 9-й по 11-ю минуту. Это время попадает в интервал 8–12 мин. Значит, имеем пару для ответа: Б–1 .
- Скорость 20 км/ч и больше автобус имел в течение нескольких временных промежутков. Причем вариант А здесь не подходит, т.к., к примеру, на 7-й минуте скорость составляла 60 км/ч, вариант Б – потому что он уже применен, вариант Г – потому что в начале и конце промежутка автобус имел нулевую скорость. В данном случае подходит вариант В (12–16 мин); на этом промежутке автобус начинает движение со скоростью 40 км/ч, далее ускоряется до 100 км/м и потом постепенно снижает скорость до 20 км/ч. Итак, имеем: В–2 .
- Здесь установлено ограничение для скорости. При этом варианты Б и В мы не рассматриваем. Оставшиеся же интервалы А и Г подходят оба. Поэтому правильно будет рассмотреть сначала 4-й вариант, а потом снова вернуться в 3-му.
- Из двух оставшихся интервалов для характеристики №4 подходит только 4–8 мин, поскольку на этом промежутке остановка была (на 6-й минуте). На промежутке 18–22 мин остановок не было. Получаем: А–4 . Отсюда следует, что для характеристики №3 нужно взять интервал Г, т.е. получается пара Г–3 .
Вариант 14МБ7
На рисунке точками показан прирост населения Китая в период с 2004 по 2013 год. По горизонтали указывается год, по вертикали – прирост населения в процентах (увеличение численности населения относительно прошлого года). Для наглядности точки соединены линией.
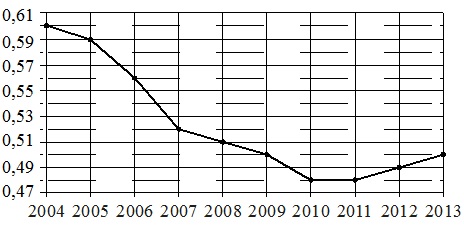
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику прироста населения Китая в этот период .

Алгоритм выполнения
- Определяем цену деления вертикальной шкалы рисунка. Находится она как разница пары соседних значений шкалы, деленная на 2 (т.к. между двумя соседними значениями имеется 2 деления).
- Анализируем последовательно приведенные в условии характеристики 1–4 (левая табличная колонка). Сопоставляем каждую из них с конкретным периодом времени (правая табличная колонка).
Решение:
Цена деления вертикальной шкалы составляет 0,01%.
- Падение прироста непрерывно продолжалось с 2004 по 2010 год. В 2010–2011 годах прирост был стабильно минимальным, и начиная с 2012 года оно начал увеличиваться. Т.е. остановка прироста произошла в 2010 году. Этот год находится в периоде 2009–2011 гг. Соответственно, имеем: В–1 .
- Наибольшим падением прироста следует считать самую «круто» падающую линию графика на рисунке. Она приходится на период 2006–2007 гг. и составляет 0,04%, за год (0,59–0,56=0,04% в 2006 г. и 0,56–0,52=0,04% в 2007 г.). Отсюда получаем: А–2 .
- Указанный в характеристике №3 прирост начался с 2007 года, продолжился в 2008 г. и завершился в 2009 году. Это соответствует периоду времени Б, т.е. имеем: Б–3 .
- Прирост населения начал увеличиваться после 2011 г., т.е. в 2012–2013 гг. Поэтому получаем: Г–4 .
Вариант 14МБ8
На рисунке изображены график функции и касательные, проведенные к нему в точках с абсциссами А,В,С и D.

В правом столбце указаны значения производной функции в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.

Алгоритм выполнения
- Рассматриваем пару касательных, имеющих острый угол с положит.направлением оси абсцисс. Сравниваем их, находим соответствие среди пары соответствующих значений производных.
- Рассматриваем пару касательных, образующих с положит.направлением оси абсцисс тупой угол. Сравниваем их по модулю, определяем соответствие их значениям производных среди двух оставшихся в правой колонке.
Решение:
Острый угол с положит.направлением оси абсцисс образуют производные в т.В и т.С. Эти производные имеют положит.значения. Поэтому выбирать тут следует между значениями №№1 и 3. Применяя правило о том, что если угол меньше 45 0 , то производная меньше 1, а если больше, то больше 1, делаем вывод: в т.В производная по модулю больше 1, в т.С – меньше 1. Это означает, что можно составить пары для ответа: В–3 и С–1 .
Производные в т.А и т.D образуют с положит.направлением оси абсцисс тупой угол. И тут применяем то же правило, немного перефразировав его: чем больше касательная в точке «прижата» к линии оси абсцисс (к отрицат. ее направлению), тем больше она по модулю. Тогда получаем: производная в т.А по модулю меньше, чем производная в т.D. Отсюда имеем пары для ответа: А–2 и D–4 .
Вариант 14МБ9
На рисунке точками показана среднесуточная температура воздуха в Москве в январе 2011 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения температуры .

Алгоритм выполнения
Анализируем последовательно характеристики 1–4 (правая колонка), используя график на рисунке. Ставим каждой из них в соответствие конкретный временной период (левая колонка).
Решение:
- Рост температуры наблюдался только в конце периода 22–28 января. Здесь 27 и 28 числа она повышалась соответственно на 1 и на 2 градуса. В конце периода 1–7 января температура была стабильной (–10 градусов), в конце 8–14 и 15–21 января понижалась (с –1 до –2 и с –11 до –12 градусов соответственно). Поэтому получаем: Г–1 .
- Поскольку каждый временной период охватывает 7 дней, то анализировать нужно температуру, начиная с 4-го дня каждого периода. Неизменной в течение 3–4 дней температура была только с 4 по 7 января. Поэтому получаем ответ: А–2 .
- Месячный минимум температуры наблюдался 17 января. Это число входит в период 15–21 января. Отсюда имеем пару: В–3 .
- Температурный максимум пришелся 10 января и составил +1 градус. Эта дата попадает в период 8–14 января. Значит, имеем: Б–4.
Вариант 14МБ10
Алгоритм выполнения
- Значение функции в точке положительно, если эта точка расположена выше оси Ох.
- Производная в точке больше нуля, если касательная к этой точке образует острый угол с положительным направлением оси Ох.
Решение:
Точка А. Она находится ниже оси Ох, значит значение функции в ней отрицательно. Если провести в ней касательную, то угол между нею и положит.направлением Ох составит около 90 0 , т.е. образует острый угол. Значит, в данном случае подходит характеристика №3. Т.е. имеем: А–3 .
Точка Б. Она находится над осью Ох, т.е. точка имеет положит.значение функции. Касательная в этой точке будет довольно близко «прилегать» к оси абсцисс, образуя тупой угол (немногим меньше 180 0) с положительным ее направлением. Соответственно, производная в этой точке отрицательна. Т.о., здесь подходит характеристика 1. Получаем ответ: В–1 .
Точка С. Точка расположена ниже оси Ох, касательная в ней образует большой тупой угол с положит.направлением оси абсцисс. Т.е. в т.С значение и функции, и производной отрицательно, что соответствует характеристике №2. Ответ: С–2 .
Точка D. Точка находится выше оси Ох, а касательная в ней образует с положит.направлением оси острый угол. Это говорит о том, что как значение функции, так и значение производной здесь больше нуля. Ответ: D–4 .
Вариант 14МБ11
На рисунке точками показаны объемы месячных продаж холодильников в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных холодильников. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж холодильников .
Муниципальное общеобразовательное учреждение
«Салтыковская средняя общеобразовательная школа
Ртищевского района Саратовской области»
Мастер – класс по математике
в 11 классе
по теме
«ПРОИЗВОДНАЯ ФУНКЦИИ
В ЗАДАНИЯХ ЕГЭ»
Провела учитель математики
Белоглазова Л.С.
2012-2013 учебный год
Цель мастер – класса : развивать у учащихся навыкиприменения теоретических знаний по теме «Производная функции» для решения задач единого государственного экзамена.
Задачи
Образовательные: обобщить и систематизировать знания учащихся по теме
«Производная функции», рассмотреть прототипы задач ЕГЭ по данной теме, предоставить обучающимся возможность проверить свои знания при самостоятельном решении задач.
Развивающие: способствовать развитию памяти, внимания, навыков самооценки и самоконтроля; формированию основных ключевых компетенций (сравнение, сопоставление, классификация объектов, определение адекватных способов решения учебной задачи на основе заданных алгоритмов, способность самостоятельно действовать в ситуации неопределённости, контролировать и оценивать свою деятельность, находить и устранять причины возникших трудностей).
Воспитательные: способствовать:
формированию у учащихся ответственного отношения к учению;
развитию устойчивого интереса к математике;
созданию положительной внутренней мотивации к изучению математики.
Технологии : индивидуально–дифференцированного обучения, ИКТ.
Методы обучения : словесный, наглядный, практический, проблемный.
Формы работы: индивидуальная, фронтальная, в парах.
Оборудование и материалы для урока: проектор, экран, ПК для каждого ученика, тренажёр (Приложение №1), презентация к уроку (Приложение №2), индивидуально – дифференцированные карточки для самостоятельной работы в парах (Приложение №3), список сайтов сети Интернет, индивидуально-дифференцированное домашнее задание (Приложение №4).
Пояснение к мастер - классу. Данный мастер – класс проводится в 11 классе с целью подготовки к ЕГЭ. Нацелен на применение теоретического материала по теме «Производная функции» при решении экзаменационных задач.
Продолжительность мастер – класса – 30 мин.
Структура мастер - класса
I .Организационный момент -1 мин.
II .Сообщение темы, цели мастер - класса, мотивация учебной деятельности-1 мин.
III . Фронтальная работа. Тренинг «Задания В8 ЕГЭ». Анализ работы с тренажёром - 6 мин.
IV .Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач В14. Взаимопроверка - 7 мин.
V . Проверка индивидуального домашнего задания. Задача с параметром С5 ЕГЭ
3 мин.
VI .Оn – line тестирование. Анализ результатов тестирования - 9 мин.
VII . Индивидуально – дифференцированное домашнее задание -1 мин.
VIII .Оценки за урок - 1 мин.
IX .Итог урока. Рефлексия -1 мин.
Ход мастер - класса
I.Организационный момент.
II.Сообщение темы, цели мастер - класса, мотивация учебной деятельности.
(Слайды 1-2,пр иложение №2)
Тема нашего занятия «Производная функции в заданиях ЕГЭ». Всем известно высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении многих практических задач математики, физики, химии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно.
Тема «Производная» представлена в заданиях части В (В8, В14) единого государственного экзамена. Некоторые задания С5 также можно решить с применением производной. Но для решения этих задач требуется хорошая математическая подготовка и нестандартное мышление.
Вы работали с документами, регламентирующими структуру и содержание контрольных измерительных материалов единого государственного экзамена по математике 2013. Сделайте вывод о том, какие знания и умения вам нужны для успешного решения задач ЕГЭ по теме «Производная» .
(Слайды 3-4, п риложение №2)
Мы изучили «Кодификатор элементов содержания по МАТЕМАТИКЕ для составления контрольных измерительных материалов для проведения единого государственного экзамена»,
«Кодификатор требований к уровню подготовки выпускников», «Спецификацию контрольных измерительных материалов», «Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2013» и выяснили, какие знания и умения о функции и её производной нужны для успешного решения задач по теме «Производная».
Необходимо
ЗНАТЬ
п равила вычисления производных;
производные основных элементарных функций;
геометрический и физический смысл производной;
уравнение касательной к графику функции;
исследование функции с помощью производной.
УМЕТЬ
выполнять действия с функциями (описывать по графику поведение и свойства функции, находить её наибольшее и наименьшее значения).
ИСПОЛЬЗОВАТЬ
приобретенные знания и умения в практической деятельности и повседневной жизни.
Вы владеете теоретическими знаниями по теме «Производная». Сегодня мы будем УЧИТЬСЯ ПРИМЕНЯТЬ ЗНАНИЯ О ПРОИЗВОДНОЙ ФУНКЦИИ ДЛЯ РЕШЕНИЯ ЗАДАЧ ЕГЭ. ( Слайд 4, приложение №2)
Ведь недаром Аристотель говорил, что “УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО В ЗНАНИИ, НО И В УМЕНИИ ПРИМЕНЯТЬ ЗНАНИЯ НА ПРАКТИКЕ” ( Слайд 5, приложение №2)
В конце урока мы вернёмся к цели нашего занятия и выясним, достигли ли её?
III . Фронтальная работа. Тренинг «Задания В8 ЕГЭ» (Приложение №1) . Анализ работы с тренажёром.
Выберите правильный ответ из четырёх предложенных.
В чём, по вашему мнению, заключается сложность выполнения задания В8?
Как вы думаете, какие типичные ошибки допускают выпускники на экзамене при решении этой задачи?
При ответах на вопросы задания В8 вы должны уметь описывать по графику производной поведение и свойства функции, а по графику функции – поведение и свойства производной функции. А для этого нужны хорошие теоретические знания по следующим темам: «Геометрический и механический смысл производной. Касательная к графику функции. Применение производной к исследованию функций».
Проанализируйте, какие задания вызвали у вас затруднения?
Какие теоретические вопросы вам необходимо знать?
IV . Индивидуально - дифференцированная работа в парах. Самостоятельное решение задач В14. Взаимопроверка. (Приложение №3)
Вспомните алгоритм решения задач (В14 ЕГЭ) на нахождение точек экстремума, экстремумов функции, наибольшего и наименьшего значений функции на промежутке с помощью производной.
Решите задачи с помощью производной.
Перед учащимися поставлена проблема:
«Подумайте, можно ли решить некоторые задачи В14 другим способом, без применения производной?»
1 пара (Лукьянова Д., Гаврюшина Д.)
1)В14. Найдите точку минимума функции у =10х-ln (х+9)+6
2)В14. Найдите наибольшее значение функции y =
- Попытайтесь решить вторую задачу двумя способами.
2 пара (Санинская Т., Сазанов А.)
1)В14. Найдите наименьшее значение функции у=(х-10) на отрезке
2)В14. Найти точку максимума функции у= -
![]()
(Учащиеся защищают своё решение, записывая основные этапы решения задач на доске. Учащиеся 1 пары (Лукьянова Д., Гаврюшина Д.) предоставляют два способа решения задачи №2).
Разрешение проблемы. Вывод, который должны сделать учащиеся:
«Некоторые задачи В14 ЕГЭ на нахождение наименьшего и наибольшего значения функции можно решить без применения производной, опираясь на свойства функций».
Проанализируйте, какая ошибка была допущена вами в задаче?
Какие теоретические вопросы вам необходимо повторить?
V . Проверка индивидуального домашнего задания. Задача с параметром С5(ЕГЭ) (Слайды 7-8, приложение №2 )
Лукьяновой К. было дано индивидуальное домашнее задание: из пособий по подготовке к ЕГЭ выбрать задачу с параметром (С5) и решить её с помощью производной.
(Учащаяся приводит решение задачи, опираясь на функционально - графический метод, как один из методов решения задач С5 ЕГЭ и даёт краткое объяснение данного метода).
Какие знания о функции и её производной необходимы при решении задач С5 ЕГЭ?
V I. Оn – line тестирование по заданиям В8, В14. Анализ результатов тестирования.
Сайт для тестирования на уроке:
Кто не допустил ошибок?
Кто испытывал трудность при тестировании? Почему?
В каких заданиях допущены ошибки?
Сделайте вывод, какие теоретические вопросы вам необходимо знать?
VI I. Индивидуально – дифференцированное домашнее задание
(Слайд 9, приложение №2 ), (Приложение №4).
Я подготовила список сайтов сети интернет для подготовки к ЕГЭ. Вы можете также проходить на этих сайтах О n – line тестирование. К следующему уроку вам нужно: 1) повторить теоретический материал по теме «Производная функции»;
2) на сайте «Открытый банк заданий по математике» ( ) найти прототипы заданий В8 и В14 и решить не менее 10 задач;
3) Лукьяновой К., Гаврюшиной Д. решить задачи с параметрами. Остальным учащимся решить задачи 1-8 (вариант 1).
VI II. Оценки за урок.
Какую оценку за урок ты бы себе поставил?
Как ты думаешь, можно было бы тебе работать на уроке лучше?
IХ. Итог урока. Рефлексия
Подведем итог нашей работы. Какова была цель урока? Как вы считаете, достигнута ли она?
Посмотрите на доску и одним предложением, выбирая начало фразы, продолжите предложение, которое вам больше всего подходит.
Я почувствовал…
Я научился…
У меня получилось …
Я смог…
Я попробую …
Меня удивило, что …
Мне захотелось…
Можете ли вы сказать, что в ходе урока произошло обогащение запаса ваших знаний?
Итак, вы повторили теоретические вопросы о производной функции, применили свои знания при решении прототипов заданий ЕГЭ (В8, В14), а Лукьянова К. выполнила задачу С5 с параметром, которая является задачей повышенной степени сложности.
Мне приятно было с вами работать, и надеюсь, что знания, полученные на уроках математики, вы сможете успешно применить не только при сдаче ЕГЭ, но и в дальнейшей своей учёбе.
Закончить урок мне хотелось бы словами итальянского философа Фомы Аквинского «Знание – столь драгоценная вещь, что его не зазорно добывать из любого источника» (Слайд 10, приложение №2).
Желаю успехов в подготовке к ЕГЭ!









