Тема: Методы использования ограниченности функций.
Жизнь хороша тем, что в ней можно заниматься математикой. (Леонард Эйлер) Цели : развитие нового нешаблонного мышления, которое можно успешно применять и в других сферах человеческой деятельности (кибернетика, вычислительная техника, экономика, радиофизика, химия и др).
Задачи : - обучение оценке объективной и субъективной трудности заданий и, разумному выбору этих заданий на экзамене;

Создание «копилки» нетрадиционных и необычных рассуждений.

Ход урока:

    Орг. момент. Формулирование учащимися темы урока посредством выполнения заданий ЕГЭ части А и В и расшифровке темы по убыванию полученных ответов. (В качестве предполагаемых слов зашифровать 12 карточек под номерами от -2 до 10) (приложение 1 и 2)

ограниченности

2. Разделить учащихся на 2 группы, вручить им набор « Теория + 10 заданий» (приложение 3 и 4 ), попросить выбрать те задания, которые можно выполнить по данной теоретической части, обосновать свой выбор. 3. Показать ход выполнения этих заданий на доске учащимися: Носкова К. , Дедевшин И., Веселов И. 4. Разделить задания из карточки на 2 группы для решения их с последующей самопроверкой по листу готовых решений. (приложение 5) 5. Раздать группам листы с описанием новых нестандартных методов решения уравнений и неравенств для выбора следующей темы (в качестве дом. задания отыскать в сборниках ЕГЭ задачи, которые можно решать этим методом)(приложение 6) 6. Рефлексия учащихся (заполнение таблички) Ф.И. учащегося

Приложение 1.
Решите эти задания и расположите ответы в порядке убывания, соберите по ответам тему нашего занятия.

Найти абсциссу точки графика функции у=3х 2 -7х+7, в которой тангенс угла касательной равен -1.

Приложение 2.
9 2 0 7Исследование функций с помощью производной. 10 5 1 -1Метод использования ограниченности функций. 4 -2 8 12Решение неравенств графическим способом.
3 11 6Решения функциональных уравнений.
Исследование


Приложение 3.

Одним из эффективных методов решения уравнений или неравенств является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся, например, некоторые тригонометрические; обратные тригонометрические функции; функции, содержащие модуль, степень, корень с чётной степенью и другие.

Наиболее распространёнными неравенствами являются следующие:

│f(x) │≥ 0, -1 ≤ sinx≤ 1, -1 ≤ cosx≤ 1, -

-

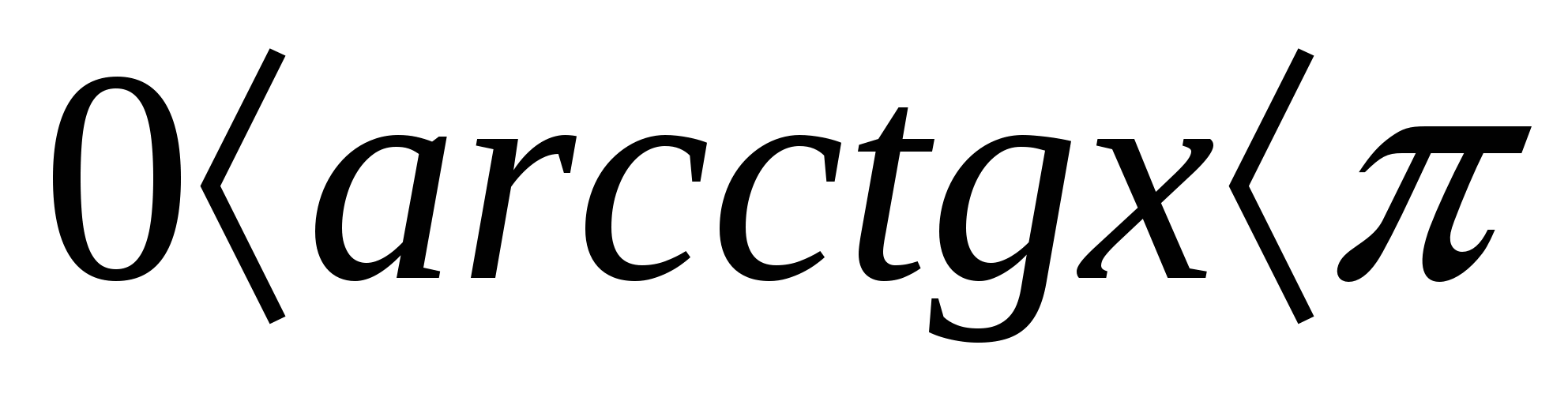, a f ( x ) >0, (f(x) ± g(x)) 2 n ≥ 0,
, a + ≥ 2, b + ≤ -2 и многие другие. Здесь n-натуральное число, h(x) ≥ 0, a >0, b 0.

Кроме приведённых простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства -,

,

и неравенства с модулями вида
.

Пример 1. Решить уравнение:

Решение: выделим полный квадрат в правой части уравнения, т.е. . Отсюда следует, что
. Так как при этом sinπ x≤ 1, то получаем систему уравнений

Решая второе уравнение системы, получаем что х=. Подстановкой в первое уравнение убеждаемся, что найденное значение х является решением системы, а значит, является решением исходного уравнения.

Ответ: х=.

Пример 2. Решить уравнение:

Решение : так как Однако sin2 π x≤ 1. Поэтому, 5+4 sin2 π x≤ 9. Таким образом, получаем систему уравнений:

Отсюда получаем систему уравнений
, из первого уравнения найдём х=. Подставим его во второе уравнение системы и убедимся, что х= является решением системы, а значит, является решением исходного уравнения.

Ответ: х=

Приложение 4. Из предложенного списка заданий выберите те, которые можно решить и использованием метода ограниченности функций. 1. Решить уравнение х 2 -4 x=(2-cos
2. Найти количество целочисленных решений неравенства х 2 ctg 2
3. Решить уравнение
4. Решить уравнение 3-( 5. Найти количество целочисленных решений неравенства 16-х 2 ≥0, удовлетворяющих условию 3 tg 2
6. Решить уравнение
7. Решить уравнение -25х 2 +40х-23=(cos
8. Найти произведение корней уравнения х
9. Решить уравнение
10. Решить уравнение 3- cos 2

Лист самопроверки. Приложение 5. 1. Решить уравнение Решение: т.к. , то т.к. и, то
получаем систему уравнений

решаем первое уравнение, получаем х= , подставим это значение во второе уравнение


2 . Решить уравнение 3- cos 2 Решение: т.к. , то т.к. и, то
получаем систему уравнений

решаем второе уравнение, получаем х= , подставим это значение в первое уравнение

значит х= является решением исходного уравнения. Ответ: х=
3 . Найти количество целочисленных решений неравенства х 2 +7х-8≤0, удовлетворяющих условию ctg 2 Решение: т.к. и то при любых допустимых значениях хНайдём нули квадратного трёхчлена, по теореме ВиетаРешим неравенство методом интервалов
т.о. хзнаем, что
целочисленные значения х - это числаисключаем Ответ: 8 целочисленных решений4 . Найти количество целочисленных решений неравенства 16-х 2 ≥0, удовлетворяющих условию 3 tg 2 Решение: т.к. и то при любых допустимых значениях хНайдём нули выражения, х= и х=Решим неравенство методом интервалов
т.о. хзнаем, что

целочисленные значения х - это числаисключаем Ответ: 7 целочисленных решений
Приложение 6.

Метод использования монотонности функций. При решении уравнения типа f(x)=g(x) в ряде случаев эффективным является метод, который использует монотонность функций у= f(x) и у= g(x).Если функция у= f(x) непрерывна и возрастает (убывает) на отрезке a ≤ x≤ b , а функция у= g(x) непрерывна и убывает (возрастает) на этом же отрезке, то уравнение f(x)=g(x) на отрезке a ≤ x≤ b может иметь не более одного корня, значит необходимо или попытаться подбором найти единственный корень уравнения, или показать, что такого корня не существует. Особенно этот метод эффективен в том случае, когда обе части уравнения f(x)=g(x) представляют собой «неудобные» для совместного исследования функции.Замечание: Если функция у= f(x) возрастает, а функция у= g(x) убывает для a ≤ x≤ b и при этом f (а)> g (а) , то корней уравнения среди a ≤ x≤ b нет.

Пример : Решить уравнение Решение: Областью допустимых значений уравнения являются х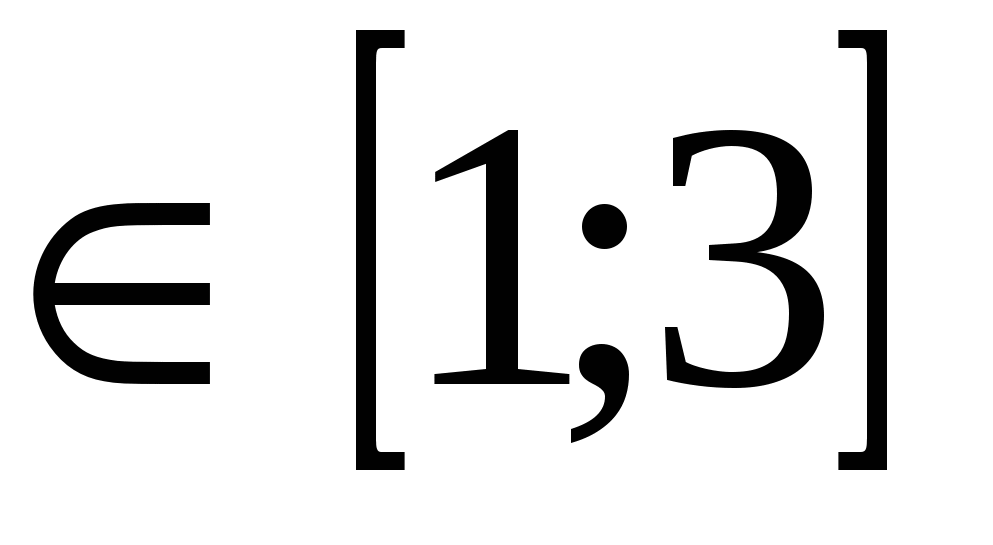
. Нетрудно видеть, что на этой области левая часть уравнения возрастает, а правая - убывает, т.е. функция f (x )=
является возрастающей, а функция g (x )=
- убывающая. В этой связи исходное уравнение может иметь только один корень (если он есть). Подбором находим этот корень уравнения х= 2.Ответ : х=2
Метод решения функциональных уравнений. К числу наиболее сложных задач на ЕГЭ относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида f(f(….f(x)…))=x или f(g(x))=f(h(x)), где f(x),g(x),h(x)- некоторые функции и n≥ 2
Методы решения этих функциональных уравнений основаны на применении многих теорем, рассмотрим одну из них.
Теорема1. Корни уравнения f (x )=0 являются корнями уравнения f(f(….f(x)…))=x
Пример : Решить уравнение х=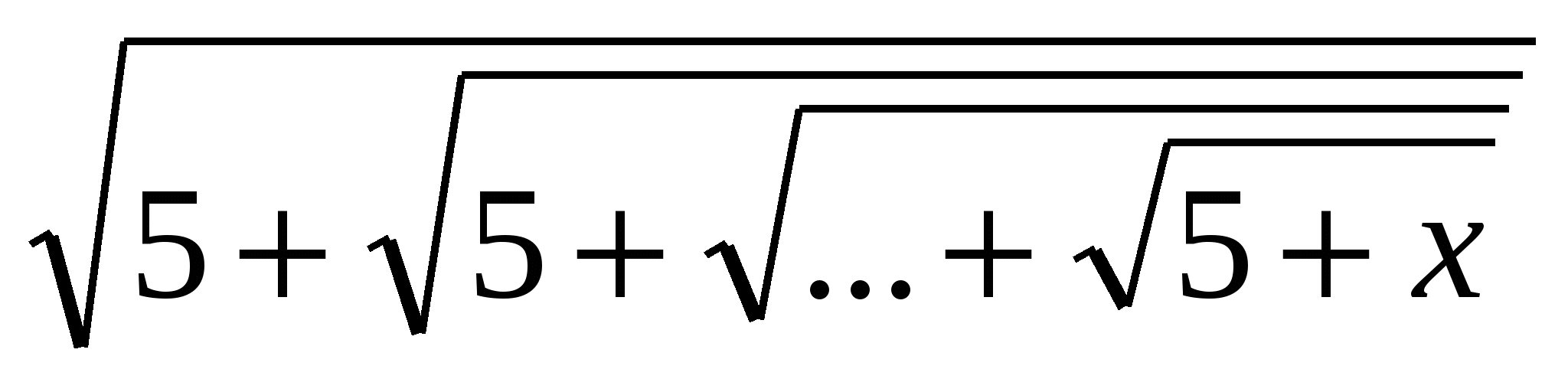
 , где квадратный корень берётся n раз и n ≥ 1 Решение: Из условия задачи следует, что х > 0. Пусть f (x )=
, тогда наше уравнение можно представить в виде функционального f ( f (…. f ( x )…))= x . Так как при х > 0 функция f (x )= возрастает и f (x ) > 0, то уравнение х= равносильно уравнению f (x )= x , т.е. =х, положительным решением которого является х=
Ответ: х=

Раздел I. Математика и физика

УДК 372.8 ББК 74.262.21

Н.Е. Ляхова, А.И. Гришина, И.В. Яковенко

ИСПОЛЬЗОВАНИЕ ОГРАНИЧЕННОСТИ ФУНКЦИЙ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ

Аннотация. В статье представлена методика изучения метода решения «нестандартных» уравнений элементарной математики с использованием ограниченности функций.

Ключевые слова: решение уравнений, использование ограниченности функции.

N.E. Lyakhova, A.I Grishina, I.V. Yakovenko

USE OF LIMITATION OF FUNCTIONS IN THE SCHOOL COURSE OF MATHEMATICS

Abstract. The paper presents a methodology for studying the method for solving the "nonstandard" equations of elementary mathematics with limited functions. Key words: solution of equations, using a limited function.

Ограниченность функций позволяет решать многие нестандартные уравнения и неравенства, одновременно содержащие разнообразные функции, что не позволяет применить к ним стандартные методы решения задачи определенного типа. На использовании ограниченности функций построены такие методы решения уравнений и неравенств, как метод мини-максов и его следствия. Название метода - метод мини-максов - возможно, спорное, но оно позволяет быстро вспомнить суть метода и служит для ученика опорным знаком. Отметим, что изучение этого метода полезно для выпускника школы как с точки зрения расширения его возможностей по решению «нестандартных» задач, так и с точки зрения формирования навыков исследования функции (в особенности методами элементарной математики). И то и другое важно для подготовки выпускника к ЕГЭ по математике, так как контрольно - измерительные материалы традиционно содержат подобные задания, в то время как в школьных учебниках они представлены явно недостаточно либо не представлены совсем.

Суть метода мини-максов заключается в следующем утверждении.

Утверждение 1. Если на области определения X уравнения

а функция

то данное уравнение равносильно системе

f (*) = а g(*) = а "

Действительно, при указанных условиях равенство

возможно тогда и только тогда, когда функции f (*) и g (*) при одном и том же значении * принимают значение а. При этом число а будет являться для функций f (*) и g (*) соответственно наибольшим и наименьшим значениями на множестве X. Заметим, что в случае, если хотя бы одна из функций f (*) или g (*) на множестве X не принимает значение а, то уравнение

не имеет корней. Но в этом случае система также не имеет решений и, следовательно, равносильность уравнения и системы не нарушается. Поэтому при получении необходимых оценок нет необходимости устанавливать, что а является на множестве X наибольшим значением функции f(*) и наименьшим значением функции g(*) .

Используя утверждение 1 и свойства числовых неравенств, нетрудно доказать еще два утверждения, которые являются следствиями метода мини-максов.

Утверждение 2. Пусть множество X - пересечение областей определения функций f (х) и g (х), и на этом множестве имеют место неравенства

тогда неравенство

f (х) + g (х) > а + Ь,

равносильно уравнению

f (х) + g (х) = а + Ь, которое, в свою очередь, равносильно системе:

/ (х) = а, ё (х) = Ь.

Утверждение 3. Пусть множество X - пересечение областей определения функций f (х) и ё (х), и на этом множестве имеют место неравенства

0 < f (х) < а

ё (х) < Ь, где а > 0 , Ь > 0

тогда неравенство

f (х) ё (х) > а Ь

будет равносильно уравнению

f (х) ё (х) = а Ь, которое, в свою очередь, равносильно системе

/ (х) = а, ё(х) = Ь.

Как видно из формулировок утверждений, для реализации метода мини-максов (или его следствий) необходимо производить оценки функций, входящих в уравнения или неравенства. Фактически оценка функций является основным действием при реализации метода. Поэтому и обучение методу необходимо построить на выработке навыков оценки различных функций. На наш взгляд наиболее актуальными для школьников будут следующие приемы такой оценки.

1. Простейший прием - оценка функции вида f (х) = А ± а(х), где а(х) - некоторая неотрицательная функция.

5. Оценка сложной функции.

Остановимся подробнее на каждом приеме, проиллюстрируем его на примерах и приведем набор тренировочных упражнений для выработки навыков решения уравнений с использованием этого приема.

1. Простейший прием оценки функции. Пусть а(х) - некоторая неотрицательная функция, тогда:

Если f (х) = А + а(х), то f (х) > А;

Если f (х) = А - а(х), то f (х) < А.

Первый прием мы назвали простейшим, так как оценка в этом случае практически очевидна при условии, что ученику известен набор неотрицательных функций: 24х, х2", х~2", ха (гдеаеЩ-), |х|, |х| -х, arccosх, агс^х, ах и др. Кроме того, неотрицательные значения будут принимать сложные функции, являющиеся результатом композиции функций, если последняя функция композиции неотрицательна. Таким образом, список неотрицательных функций можно

обобщить: 2^и(х) , (ы(х))2" , (м(х))-2я,агеео8и(х), агссгёи(х), |и(х)|, |и(х) -и(х) , а"(х), (и(х))а (гдеае к).

Приведем примеры на использование метода мини-максов, при решении которых применяется рассмотренный прием оценки.

Пример 1. Решить уравнение 2 + |х(х -1)| = 2 - ^(х -1)(х + 2) . Решение. Функции

/ (х) = |х(х -1)|, Я (х) = 7 (х -1)(х + 2)

неотрицательны. Следовательно, имеет место следующая оценка левой и правой частей уравнения

2 + | х(х -1)| > 2,

2-у/(х-1)(х + 2) < 2 "

Тогда, согласно утверждению 1, исходное уравнение равносильно системе

Тогда:

Если функция f (u) возрастает на отрезке то имеет место неравенство

f (a) < f (u(x)) < f (b);

Если функция f (u) убывает на отрезке , то имеет место неравенство

f (b) < f (u(x)) < f (a) .

Пример 7. Решить уравнение log2 (x2 - 6x+11) = cos((x - 3) sin x).

Решение. Выделяя полный квадрат в квадратном трехчлене, стоящем под знаком логарифма, получим уравнение

log2 (2+(x - 3)2) = cos((x - 3) sin x). Оценим функции, стоящие в левой и правой частях этого уравнения.

f (x) = log2 (2+(x - 3)2) > 1. Действительно, 2 + (x - 3)2 > 2, функция log2 u возрастает, следовательно,

log2 (2+(x - 3)2) > log2 2 = 1. Функция u2 -монотонновозрастаетна . Графиком функции является парабола, ветви которой направлены вверх, вершина параболы (-1;-1), следовательно, на отрезке [-1;1] функция возрастает. Поэтому свое наименьшее значение принимает при t=-1,у=-1, а наибольшее значение при t=1, у=3. Ответ:E(y)=[-1;3]. =


Найти наибольшее и наименьшее значение функции на промежутке . Решение. Функция y принимает наибольшее значение, если знаменатель дроби принимает наименьшее значение. Рассмотрим знаменатель. Функции возрастающие, следовательно, их сумма – функция возрастающая, значит своё наименьшее значение она принимает на левом конце отрезка, при x=1, т.е. наименьшее значение равно 5. Следовательно, наибольшее значение исходной функции на равно 8. Ответ: 8.


ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИИ ДЛЯ НАХОЖДЕНИЯ ЕЁ НАИБОЛЬШЕГО ЗНАЧЕНИЯ Данная функция принимает наибольшее значение тогда и только тогда, когда наибольшее значение принимает функция, стоящая в показателе степени: Укажите наибольшее целое значение функции Преобразуем её: Так как то наибольшее значение функции равно 4. Следовательно, наибольшее значение исходной функции равно Ответ: Решение.


Применение свойства ограниченности функций к решению уравнений и неравенств МЕТОД МАЖОРАНТ (МЕТОД ОЦЕНКИ) Основная идея метода мажорант состоит в следующем: Пусть мы имеем уравнение f(x)=g(x) и существует такое число М, что для любого х из области определения f(x) и g(x) имеем f(x) M и g(x) M. Тогда уравнение f(x)=g(x) равносильно системе


Решить уравнения


Решить уравнение Решение: Решение: Оценим обе части уравнения. При всех значениях х верны неравенства Следовательно, данное уравнение равносильно системе: При х = 0 второе уравнение обращается в верное равенство, значит, х = 0 корень уравнения. Ответ: х = 0.




Решить уравнение. Решение. Рассмотрим функцию. Найдём координаты вершины параболы. x 0 = 7, y 0 = 25. ветви направлены вверх, следовательно наименьшее значение функции равно 25. Так как f(x) 25, то. Очевидно, 1. Значит исходное уравнение имеет корни при условии, что второе слагаемое равно 1, а первое равно 0. x-7=0, x=7 При x=7 второе слагаемое равно 1. Таким образом x=7 корень уравнения.


Решить уравнение Решение. Корень уравнения легко угадать – это x = 1. Но доказать его единственность из соображений монотонности не удается, потому что ни левая, ни правая части уравнения не являются монотонными функциями. Здесь используется другая идея. Преобразуем уравнение: Наибольшее значение правой части полученного уравнения равно 1 и принимается в точке x = 1. Выражение под логарифмом равно при x > 0. Поэтому левая часть достигает при x = 1 своего наименьшего значения, которое также равно 1. Вывод: равенство выполняется тогда и только тогда, когда обе части одновременно равны 1, т. е. при x = 1. 0. Поэтому левая часть достигает при x = 1 своего наименьшего значения, которое также равно 1. Вывод: равенство выполняется тогда и только тогда, когда обе части одновременно равны 1, т. е. при x = 1.">


Проверим справедливость первого равенства, подставив эти корни. При Решите уравнение Решение. Для решения уравнения оценим его части: Поэтому равенство возможно только при условии: Сначала решим второе уравнение: Корни этого уравнения и получаем: (верное равенство). Итак, данное уравнение имеет единственный корень х = 0. Ответ: 0. При х = -1 имеем: (не верное равенство). cos() [-1;1] cos 2 () . сумма единицы и неотрицательного числа.


Решить уравнение. Решение. (сумма двух взаимно обратных чисел). Следовательно, функция Принимает в силу непрерывности все значения из промежутка . Оценим функцию. График – парабола, ветви вверх, наименьшее значение равно 3. значит h(y) принимает наибольшее, равное 3. следовательно исходное уравнение равносильно системе.


(так как:). Решить уравнение Так как -то левая часть уравнения Для правой части (в силу неравенства для суммы двух взаимно обратных чисел) выполнено Поэтому уравнение имеет решения, если и только если одновременно выполнены два условия Решая последнюю систему, получаем принимает значение от 0,5 до 2 Ответ: Решение. Оценим обе части уравнения.




Найдите все значения параметра а при каждом из которых неравенство имеет решение. Оценим обе части неравенства. Для этого преобразуем правую часть неравенства, выделив полный квадрат Квадратичная функция принимает наименьшее значение в вершине, оно равно 4 и достигается при, то есть при а=-6/7. Множество значений левой части неравенства составляет промежуток, следовательно, наибольшее значение равно 4. Значит, неравенство выполняется в случае равенства обоих частей, и только в том случае если а=-6/7. Ответ: а=-6/7..


Найти все значения параметра а, при каждом из которых уравнение имеет решения. Найдите эти решения. Решение. Перепишем уравнение в виде При всех значениях х выражение, поэтому. При всех значениях х выражение и. Поэтому. Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему Ответ: х=5/7 при а=-4/9.


Найдите все значения параметра Р при которых уравнение не имеет корней. Используя формулу косинуса двойного угла, преобразуем выражение Уравнение не будет иметь корни, если Р не будет принадлежать области значений левой части уравнения. Рассмотрим функцию f(x)=, оценим её. Так как Поэтому Функция f(x) непрерывна и принимает все свои значения: sinx=0, f(x)=-9, а если sinx=1, то f(x)=17,т.е. E(f)=[-9;17].Исключаем этот отрезок из числовой прямой и получаем ответ. Ответ:

Использование монотонности функций при решении уравнений и неравенств основано на следующих теоретических фактах:

  1. Строго монотонная функция принимает каждое свое значение ровно один раз.
  2. Если одна функция возрастает, а другая убывает на одном и том же промежутке, то графики их, либо только один раз пересекутся, либо вообще не пересекутся, а это означает, что уравнение F(x)=G(x) имеет не более одного решения.
  3. Если на некотором промежутке одна из функций убывает (возрастает), а другая принимает постоянные значения, то уравнение F(x)=G(x) либо имеет единственный корень, либо не имеет корней.

Пример

Решите уравнение:\({x^3} = 2 - x\)

Рассмотрим функции \(f(x) = {x^3}\) и \(g(x) = 2 - x.\)

Функция f(x) возрастает на всей области определения, а функция g(x) убывает на области определения. Следовательно, данное уравнение имеет не

более одного корня.

Подбором находим, что x=1. Проверкой убеждаемся, что x=1 действительно корень уравнения.

Проверка: 13=2-1; 1=1.

Использование четности функции

Функция f (x) называется четной, если для любого \(x \in D\)

выполняется равенство: \(f(- x) = f(x).\)

Исследование функций на четность облегчается следующими утверждениями:

·Сумма четных (нечетных) функций являет

ся четной (нечетной) функцией.

·Произведение двух четных или двух нечетных функций является четной функцией.

·Произведение четной и нечетной функции является нечетной функцией.

·Если функция f четна (нечетна), то и функция \(\frac{1}{f}\)

четна (нечетна).

Пример

Может ли при каком-нибудь значении а уравнение: \(2{x^8} - 3a{x^6} + 4{x^4} - a{x^2} = 5\) иметь 5 корней?

Обозначим \(f(x) = 2{x^8} - 3a{x^6} + 4{x^4} - a{x^2} = 5,\) где f(x) - четная функция. Если х0 - корень данного уравнения, то (-х0) - тоже корень. Значение х=0 не является корнем уравнения. Следовательно, число корней у этого уравнения при любом

действительном а четно, поэтому 5 корней оно иметь не

Использование области определения функции

Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция определена. Область определения иногда еще называют областью допустимых

значений функции. Для нахождения функции нужно проанализировать данное соответствие и установить встречающиеся запретные операции (деление на

нуль, возведение в рациональную степень

отрицательного числа, логарифмические операции над отрицательными числами и т. п.). Иногда знание позволяет доказать, что уравнение (или неравенство) не имеет

решений, а иногда позволяет найти решения уравнения (или неравенства) непосредственной подстановкой чисел.

Решите неравенство \(\sqrt {x + 3} + \sqrt{{9 - x}} < \sqrt 3 \)

ОДЗ неравенства есть все x из промежутка \(- 3 \leqslant x \leqslant 9.\)

Разобьем это множество на два промежутка и \(0 \leqslant x \leqslant 9.\)

Для х из промежутка \(- 3 \leqslant x \leqslant 0\) имеем:

\(\begin{gathered} \sqrt {x + 3} \geqslant 0; \\ \sqrt{{9 - x}} \geqslant \sqrt{9}; \\ \sqrt{9} = \sqrt 3 . \\ \end{gathered} \)

Следовательно, на этом промежутке, поэтому неравенство не имеет решений на этом промежутке.

Пусть х принадлежит \(0 \leqslant x \leqslant 9\) , тогда:

\(\begin{gathered} \sqrt {x + 3} \geqslant \sqrt 3 ; \\ \sqrt{{9 - x}} \geqslant 0. \\ \end{gathered} \)

Следовательно, \(\sqrt {x + 3} + \sqrt{{9 - x}} \geqslant \sqrt 3 \) для таких x, и, значит, на этом промежутке неравенство также не имеет решений.

Итак, неравенство решений не имеет.

Использование ограниченности функции . При решении уравнений и неравенств свойство ограниченности снизу или сверху функции на некотором множестве часто играет определяющую роль.

Если существует такое число С, что для любого \(x \in D\) выполняется неравенство f(x)\(\leqslant \) C, то функция f называется ограниченной сверху на множестве D.

Если существует такое число с, что для любого выполняется неравенство f(x) ≥с, то функция f называется ограниченной снизу на множестве D.

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y=f(x) при лежит в полосе с\(\leqslant \) f(x)\(\leqslant \) C.

Решите уравнение \(\sin ({x^3} + 2{x^2} + 1) = {x^2} + 2x + 2\)

Для любого действительного числа х имеем \(\sin ({x^3} + 2{x^2} + 1) \leqslant 1,\) \({x^2} + 2x + 2 = {(x + 1)^2} + 1 \geqslant 1.\)

Поскольку для любого значения х левая часть уравнения не превосходит единицы, а правая часть всегда не меньше единицы, то данное уравнение может иметь решение только при х=-1.

При х=-1 имеем:

\(\begin{gathered} {x^2} + 2x + 2 = 1; \\ \sin (- 1 + 2 + 1) = \sin 2 \ne 1; \\ \end{gathered} \)

т.е. уравнение корней не имеет.

«Область определения функции» - Область определения квадратичной функции – любое действительное число. Функция называется логарифмической, если переменная величина стоит под знаком логарифма. Логарифмическая функция. Функция, переменная величина которой находится в показателе степени, называется показательной. Квадратичная функция.

«Общие свойства функций» - Общие свойства функций. Найти область определения функции. Четная функция. Является ли эта функция четной или нечетной. По графику определите множество значений функции. По графику определите значения Х. По графику определите промежутки убывания функции. Функция f(x) возрастающая. Дана функция y=f(x).

«Возрастание и убывание функции» - Возрастание и убывание функции синус. Рассмотрим еще один пример. Промежутками убывания косинуса являются отрезки , n - целое. Пусть, например, функция f четна и возрастает на промежутке , где b>a?0. Возрастание и убывание функций. Возрастание и убывание функции косинус. На рисунке ниже изображен график функции, определенной на отрезке [-1;10].

«Применение непрерывности» - Значение выражения. Геометрический смысл производной. Метод интервалов. Составить уравнение касательной к графику функции. Касательная к графику функции. График близок к касательной. Формула. Вычислим по формуле. Касательной к кривой в данной точке M называется предельное положение секущей NM. Гипербола.

«Экстремум функции» - Зависимость давления газа от температуры. Тема урока: «Признаки возрастания и убывания функции. Тест. Изменение силы тока при размыкании цепи. Исследование функции на экстремум». Изменение переменного тока. План: Зависимость силы тока от напряжения. Зависимость давления газа от объёма. Тема: «Признаки возрастания и убывания функции.

«Функции и их свойства» - Независимую переменную называют - аргумент. Возрастающая функция. Определение функции. Четные и нечетные функции. Монотонность функции. Значения зависимой переменной называют значениями функции. Все значения независимой переменной образуют область определения функции -D (f). 1. Значения функции положительны.

Всего в теме 23 презентации