В более сложных структурах может потребоваться неоднократное применение теоремы разложения. Так, на рис.2.2 показано разложение относительно элемента 7 (верхняя строка), а затем по элементу 8 (нижняя строка). Получившиеся четыре подсети имеют последовательно-параллельные структуры и больше не требуют разложений. Легко видеть, что на каждом шаге число элементов в получающихся подсетях уменьшается на единицу а число подсетей, требующих дальнейшего рассмотрения удваивается. Поэтому описанный процесс в любом случае конечен, а число результирующих последовательно-параллельных структур составит 2 m , где т - число элементов, по которым пришлось провести разложение. Трудоемкость этого метода можно оценить величиной 2 m , что меньше трудоемкости полного перебора, но тем не менее все еще неприемлемо для расчета надежности реальных сетей коммутации.

Рисунок.2.2 Последовательное разложение сети

Метод сечений или совокупности путей

Рассмотрим еще один метод расчета структурной надежности сетей. Предположим, как и ранее, что необходимо определить вероятность связности сети между заданной парой узлов A,B. Критерием исправной работы сети в данном случае является наличие хотя бы одного пути передачи информации между рассматриваемыми узлами. Предположим, что имеется список возможных путей в виде перечня элементов (узлов и направлений связи), входящих в каждый путь. В общем случае пути будут зависимы, поскольку любой элемент может входить в несколько путей. Надежность R s любого s-ro пути можно вычислить по формуле последовательного соединения R s =p 1s p 2s …p ts , где p is - надежность i-го элемента s-ro пути.

Искомая надежность H AB зависит от надежности каждого пути и вариантов их пересечений по общим элементам. Обозначим надежность, которая обеспечивается первыми r путями, через H r . Добавление очередного (r+1) - го пути с надежностью R r+1 , очевидно, приведет к увеличению структурной надежности, которая теперь будет определяться объединением двух событий: исправен хотя бы один из первых r путей или исправен (r+1) - й путь. Вероятность наступления этого объединенного события с учетом возможной зависимости. отказов (r+1) - го и остальных путей

H r+i =H r +R r+i -R r+1 H r/ (r+1), (2.10)

где H r/ (r+1) - вероятность исправности хотя бы одного из первых r путей при условии, что исправен (r+1) - й путь.

Из определения условной вероятности H r/ (r+1) следует, что при ее расчете вероятность исправной работы всех элементов, входящих в (r+1) - й путь, необходимо положить равной единице. Для удобства дальнейших расчетов представим последний член выражения (2.10) в следующем виде:

R r+1 H r/ (r+1) = R r+1 ¤ H r (2.11)

где символ (¤) означает, что при перемножении показатели надежности всех элементов, входящих в первые r путей и общих с (r+l) - м путем, заменяются единицей. С учетом (2.11) можно переписать (2.10):

?H r+1 = R r+1 ¤ Q r (2.12)

где?H r+1 =H r+1 -H r - приращение структурной надежности при введении (r+1) - го пути; Q r =1 - H r вероятность того, что произойдет одновременный отказ первых r путей.

Учитывая, что приращение надежности?H r+1 численно равно уменьшению ненадежности?Q r+1 получаем следующее уравнение в конечных разностях:

?Q r+1 =R r+1 ¤ Q r (2.13)

Легко проверить, что решением уравнения (2.13) является функция

Q r = (1-R 1) ¤ (1-R 2) ¤…¤ (1-R r) (2.14)

В случае независимых путей операция символического умножения совпадает с обычным умножением и выражение (2.14) аналогично (2.4) дает коэффициент простоя системы, состоящей из параллельно включенных элементов. В общем случае необходимость учета общих элементов путей заставляет производить умножение согласно (2.14) в алгебраическом виде. При этом число членов в результирующей формуле с умножением на каждый очередной двучлен удваивается и окончательный результат будет иметь 2 r членов, что эквивалентно полному перебору совокупности всех r путей. Например, при r=10 число членов в окончательной формуле превысит 1000, что уже выходит за рамки ручного счета. С дальнейшим увеличением числа путей довольно быстро исчерпываются и возможности современных ЭВМ.

Однако свойства введенной выше операции символического умножения позволяют резко сократить трудоемкость расчетов. Рассмотрим эти свойства более подробно. Согласно операции символического умножения для показателя надежности p i любого элемента справедливо следующее правило:

p i ¤p i =p i . (2.15)

Напомним, что второй сомножитель (2.15) имеет смысл вероятности исправной работы i-го элемента при условии его исправности, которая, очевидно, равна единице.

Для сокращения дальнейших выкладок введем следующее обозначение ненадежности i-го элемента:

=1-p i (2.16)

С учетом (2.15) и (2.16) можно записать следующие простые правила преобразования выражений, содержащих р и р:

p i ¤p i =p i (2.17)

p i p j ¤ =p i p j -p i p s

Для примера использования этих правил при расчете надежности рассмотрим простейшую сеть связи, изображенную на. рис.2.3 Буквы, стоящие у ребер графа, обозначают показатели надежности соответствующих линий связи.

Узлы для простоты будем считать идеально надежными. Предположим, что для связи между узлами А и В можно использовать все пути, состоящие из трех и менее последовательно включенных линий, т.е. следует учесть подмножество путей {м} = {ab, cdf, cgb, ahf}. Определим приращение надежности, обеспечиваемое каждым последующим путем, по формуле (2.12) с учетом (2.14):

Зr+1=Rr+1¤ (¤1¤…¤) (2.18),

Рисунок.2.3 - Пример сети расчета на ограниченном подмножестве путей

Рисунок 2.4 - Пример сети для расчета надежности по полной совокупности путей, где Ri=1-R1 аналогично (2.16).

Применяя последовательно формулу (2.18) и правила символического умножения (2.17). к рассматриваемой сети, получаем

З 2 =cdf¤ () =cdf*;

З 3 =cgb¤ (¤) =cgb**;

З 4 =ahf¤ (¤¤) =ahf**.

При расчете последнего приращения мы использовали правило 4, которое можно назвать правилом поглощения длинных цепей короткими; в данном случае его применение дает b¤cgb=b. Если разрешено использование других путей, например пути cdhb, то не представляет труда рассчитать обеспечиваемое им приращение надежности?H 5 =cdhb¤ (a¤ f¤ g¤ af) = =cdfb*a*f*g. Результирующую надежность сети можно теперь вычислить как сумму приращений, обеспечиваемых каждым из рассмотренных путей:

H R =?H i (2.19)

Так, для рассмотренного примера в предположении, что надежность. всех элементов сети одинакова, т.е. a=b=c=d=f=h=g=p, получаем H 5 =p 2 +p 3 (1-p 2) + +2p 3 (1-p) (1-p 2) +p 4 (1-p) 3 . При машинной реализации в основу расчета можно также положить формулу (2.13), с учетом того, что

Q r =?Q i (2.20)

Согласно (2.13) имеем следующее рекуррентное соотношение

Q r +i =Q r -R r+1 ¤Q r . (2.21)

При начальном условии Q 0 =l на каждом последующем шаге из полученного ранее выражения для Q r следует вычесть произведение надежности очередного (r+1) - го пути на это же выражение, в котором только показатели надежности всех элементов, входящих в (r+1) - й путь, нужно положить равными единице.

В качестве примера рассчитаем надежность сети, изображенной на рис.2.4, относительно узлов А и В, между которыми имеется 11 возможных путей передачи информации. Все расчеты сведены в табл.2.1: перечень элементов, входящих в каждый путь, результат умножения надежности данного пути на значение Q r , полученное при рассмотрении всех предыдущих путей, и результат упрощения содержимого третьего столбца по правилам (2.17). Окончательная формула для q AB содержится в последней колонке, если ее читать сверху вниз. В таблице полностью приведены все выкладки, необходимые для расчета структурной надежности рассматриваемой сети.

Таблица 2.1 Результаты расчета надежности сети, изображенной на рис.2.4

Для уменьшения объема вычислений не следует без необходимости раскрывать скобки; если промежуточный результат допускает упрощения (приведение подобных членов, вынесение за скобку общего множителя и т.д.), их следует выполнить.

Поясним несколько шагов расчета. Поскольку Q 0 = 1 (при отсутствии путей сеть разорвана), то для Q 1 из (2.21) Q 1 =1- ab=ab. Делаем следующий шаг (6.21) для Q 2 =ab-fghab==ab*fgh и т.д.

Рассмотрим подробнее шаг, на котором учитывается вклад пути 9. Произведение показателей надежности составляющих его элементов, записанное во втором столбце табл.2.1, переносится в третий. Далее в квадратных скобках записана вероятность разрыва всех предыдущих восьми путей, накопленная в четвертом столбце (начиная с первой строки), с учетом правила (2.15), согласно которому показатели надежности всех элементов, вошедших в путь 9, заменяются единицами. Вклад четвертой, шестой и седьмой строк оказывается равным нулю по правилу 1. Далее выражение, стоящее в квадратных скобках, упрощается по правилам (2.17) следующим образом: b =b (fhc-hfc-fhc) =bc (h-fh) =bchf. Аналогично производится расчет относительно всех других путей.

Использование рассматриваемого метода позволяет получить общую формулу структурной надежности, содержащую в рассмотренном случае всего 15 членов вместо максимального числа 2 11 =2048, получающегося при непосредственном перемножении вероятностей отказов этих путей. При машинной реализации метода удобно представить все элементы сети в позиционном коде строкой бит и использовать встроенные булевы функции для реализации логических элементов преобразований (2.17).

До сих пор мы рассматривали показатели структурной надежности сети относительно выделенной пары узлов. Совокупность таких показателей для всех или некоторого подмножества пар может достаточно полно характеризовать структурную надежность сети в целом. Иногда используется другой, интегральный, критерий структурной надежности. По этому критерию сеть считается исправной, если имеется связь между всеми ее узлами и задается требование на вероятность такого события.

Для расчета структурной надежности по этому критерию достаточно ввести обобщение понятия пути в виде дерева, соединяющего все заданные узлы сети. Тогда сеть будет связана, если существует, по крайней мере, одно связывающее дерево, и расчет сводится к перемножению вероятностей отказа всех рассматриваемых деревьев с учетом наличия общих элементов. Вероятность. Q s отказа s-го дерева определяется аналогично вероятности отказа пути

где p is - показатель надежности i-ro элемента, входящего в s-e дерево; n s число элементов в s-м дереве.

Рассмотрим для примера простейшую сеть в виде треугольника, стороны. которого взвешены показателями надежности а, b, с соответствующих ветвей. Для связности такой сети достаточно существования, по крайней мере, одного из деревьев аb, bс, са. Используя рекуррентное соотношение (2.12), определяем вероятность связности этой сети H. cb =ab+bca+cab. Если а=b=с=р, получаем следующее значение вероятности связности, которое легко проверить перебором: H. cb =3р 2 -2р 3 .

Для расчета вероятности связности достаточно разветвленных сетей вместо перечня связывающих деревьев, как правило, удобнее пользоваться перечнем сечений {у} которые приводят к потере связности сети по рассматриваемому критерию. Легко показать, что для сечения справедливы все введенные выше правила символического умножения, только вместо показателей надежности элементов сети в качестве исходных данных следует использовать показатели ненадежности q=1-p. Действительно, если все пути или деревья можно считать включенными "параллельно" с учетом их взаимозависимости, то все сечения включены в этом смысле "последовательно". Обозначим вероятность того, что в некотором сечении s нет ни одного исправного элемента, через р s . Тогда можно записать

р s =q 1s q 2s …q ms , (2.22)

где q is - показатель ненадежности i-ro элемента, входящего в s-e сечение.

Вероятность Н cb связности сети можно тогда представить аналогично (2.14) в символическом виде

Н cb = (1-р 1 ) ¤ (1-р 2 ) ¤…¤ (1-р r ) (2.23)

где r - число рассматриваемых сечений. Другими словами, для того чтобы сеть была связна, необходимо, чтобы одновременно были исправны хотя бы по одному элементу в каждом сечении с учетом взаимной зависимости сечений по общим элементам. Формула (2.23) является в некотором смысле двойственной по отношению к формуле (2.14) и получается из последней заменой путей на сечения и вероятностей исправной работы на вероятности пребывания в состоянии отказа. Аналогично двойственным по отношению к формуле (2.21) является рекуррентное соотношение

H r+1 =H r - р r+1 ¤ H r (2.24)

Рассчитаем для примера вероятность связности рассмотренной выше треугольной сети с набором сечений ab, bc, ca. Согласно (2.23) при начальном условии H 0 =1 имеем H cd =ab-bca-cab. При одинаковых показателях ненадежности элементов сети a=b=c=q получаем H cb =1-q 2 -2q 2 (1 - q). Этот результат совпадает с ранее полученным по методу перечисления деревьев.

Метод сечений можно, конечно, применять и для расчета вероятности связности сети относительно выделенной пары узлов, особенно в тех случаях, когда число сечений в рассматриваемой сети значительно меньше числа нулей. Однако наибольший эффект в смысле сокращения трудоемкости вычислений дает одновременное использование обоих методов, которое будет рассмотрено дальше.

Найти неопределённый интеграл (множество первообразных или "антипроизводных") означает восстановить функцию по известной производной этой функции. Восстановленное множество первообразных F (x ) + С для функции f (x ) учитывает константу интегрирования C . По скорости перемещения материальной точки (производной) может быть восстановлен закон движения этой точки (первообразная); по ускорению движения точки - её скорость и закон движения. Как видно, интегрирование - широкое поле для деятельности Шерлоков Холмсов от физики. Да и в экономике многие понятия представляются через функции и их производные и поэтому, например, можно по производительности труда в определённый момент времени (производной) восстановить объём продукции, выпущенный в соответствующее время.

Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.

Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).

Существует несколько методов нахождения интеграла, из которых метод замены переменной и метод интегрирования по частям - обязательный джентльменский набор каждого, кто успешно сдал высшую математику. Однако начинать осваивать интегрирование полезнее и приятнее с применением метода разложения, основанном на следующих двух теоремах о свойствах неопределённого интеграла, которые для удобства повторим здесь.

Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

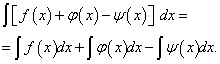(2)

Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть

(3)

Поскольку этот урок - вводный в решение задач интегрирования, важно отметить две вещи, которые либо уже на самом начальном этапе, либо несколько позже могут вас удивить. Удивление связано с тем фактом, что интегрирование - операция обратная дифференцированию и неопределённый интеграл можно справедливо называть "антипроизводной".

Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной . Это следующие формулы:

Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.

Вторая вещь, которой не следует удивляться при интегрировании . Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями . Примерами таких интегралов могут быть следующие:

Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.

Находим неопределённые интегралы вместе

Пример 1. Найти неопределённый интеграл

.

Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл 21 (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:

Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:

.

Пример 2. Найти неопределённый интеграл

Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:

Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:

.

Сокращаем получившиеся дроби и перед нами конечный ответ:

Пример 3. Найти неопределённый интеграл

Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:

Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.

Пример 4. Найти неопределённый интеграл

Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:

.

Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

Продолжаем находить неопределённые интегралы вместе

Пример 7. Найти неопределённый интеграл

Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов.

Для вычисления данного интеграла мы должны, если это возможно, пользуясь теми или другими способами, привести его к табличному интегралу и таким образом найти искомый результат. В нашем курсе мы рассмотрим лишь некоторые, наиболее часто встречающиеся приемы интегрирования и укажем их применение к простейшим примерам.

Наиболее важными методами интегрирования являются:
1) метод непосредственного интегрирования (метод разложения),
2) метод подстановки (метод введения новой переменной),
3) метод интегрирования по частям.

I. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

∫(1-√x) 2 dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫x dx+∫xdx=

Пример 3. ∫sin 2 xdx

Так как sin 2 x=(1-cos2x), то
∫sin 2 xdx=(1-cos2x)dx=∫dx-∫cos2xd(2x)=x-sin2x+C

Пример 4. ∫sinxcos3xdx

Так как sinxcos3x=(sin4x-sin2x), то имеем
∫sinxcos3xdx=∫(sin4x-sin2x)dx=∫sin4xd(4x)-∫sin2xd(2x)=-cos4x+cos2x+C

Пример 5. Найти неопределенный интеграл: ∫cos(7x-3)dx

∫cos(7x-3)=∫cos(7x-3)d(7x-3)=sin(7x-3)+C

Пример 6.

II. Метод подстановки (интегрирование заменой переменной)

Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле

∫f(x)dx=∫f(φ(t))φ"(t)dt

Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.

Пример 7. ∫x√x-5dx

Чтобы избавиться от корня, полагаем √x-5=t. Отсюда x=t 2 +5 и, следовательно, dx=2tdt. Производя подстановку, последовательно имеем:

∫x√x-5dx=∫(t 2 +5) 2tdt=∫(2t 4 +10t 2)dt=2∫t 4 dt+10∫t 2 dt=

Пример 8.

Так как , то имеем

Пример 9.

Пример 10. ∫e -x 3 x 2 dx

Воспользуемся подстановкой -x 3 =t. Тогда имеем -3x 2 dx=dt и ∫e -x 3 x 2 dx=∫e t (-1/3)dt=-1/3e t +C=-1/3e -x 3 +C

Пример 11.

Применим подстановку 1+sinx=t , тогда cosxdx=dt и

III. Метод интегрирования по частям

Метод интегрирование по частям основан на следующей формуле:

∫udv=uv-∫vdu

где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.

Пример 12. Найти неопределенный интеграл ∫xe -2x dx

Интегрирование дробно-рациональной функции.
Метод неопределенных коэффициентов

Продолжаем заниматься интегрированием дробей. Интегралы от некоторых видов дробей мы уже рассмотрели на уроке , и этот урок в некотором смысле можно считать продолжением. Для успешного понимания материала необходимы базовые навыки интегрирования, поэтому если Вы только приступили к изучению интегралов, то есть, являетесь чайником, то необходимо начать со статьи Неопределенный интеграл. Примеры решений .

Как ни странно, сейчас мы будем заниматься не столько нахождением интегралов, сколько… решением систем линейных уравнений. В этой связи настоятельно рекомендую посетить урок А именно – нужно хорошо ориентироваться в методах подстановки («школьном» методе и методе почленного сложения (вычитания) уравнений системы).

Что такое дробно-рациональная функция? Простыми словами, дробно-рациональная функция – это дробь, в числителе и знаменателе которой находятся многочлены либо произведения многочленов. При этом дроби являются более навороченными, нежели те, о которых шла речь в статье Интегрирование некоторых дробей .

Интегрирование правильной дробно-рациональной функции

Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции.

Пример 1

Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:

Сначала смотрим на числитель и выясняем старшую степень многочлена:

Старшая степень числителя равна двум.

Теперь смотрим на знаменатель и выясняем старшую степень знаменателя. Напрашивающийся путь – это раскрыть скобки и привести подобные слагаемые, но можно поступить проще, в каждой скобке находим старшую степень

и мысленно умножаем: – таким образом, старшая степень знаменателя равна трём. Совершенно очевидно, что если реально раскрыть скобки, то мы не получим степени, больше трёх.

Вывод : Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.

Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной .

Сейчас мы будем рассматривать только правильные дробно-рациональные функции . Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.

Шаг 2. Разложим знаменатель на множители. Смотрим на наш знаменатель:

Вообще говоря, здесь уже произведение множителей, но, тем не менее, задаемся вопросом: нельзя ли что-нибудь разложить еще? Объектом пыток, несомненно, выступит квадратный трехчлен. Решаем квадратное уравнение:

Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:

Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители

Начинаем оформлять решение:

Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее.

Смотрим на нашу подынтегральную функцию:

И, знаете, как-то проскакивает интуитивная мысль, что неплохо бы нашу большую дробь превратить в несколько маленьких. Например, вот так:

Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно .

Только есть одна загвоздочка, коэффициенты мы пока не знаем, отсюда и название – метод неопределенных коэффициентов.

Как вы догадались, последующие телодвижения так, не гоготать! будут направлены на то, чтобы как раз их УЗНАТЬ – выяснить, чему же равны .

Будьте внимательны, подробно объясняю один раз!

Итак, начинаем плясать от:

В левой части приводим выражение к общему знаменателю:

Теперь благополучно избавляемся от знаменателей (т.к. они одинаковы):

В левой части раскрываем скобки, неизвестные коэффициенты при этом пока не трогаем:

Заодно повторяем школьное правило умножение многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена .

С точки зрения понятного объяснения коэффициенты лучше внести в скобки (хотя лично я никогда этого не делаю в целях экономии времени):

Составляем систему линейных уравнений.
Сначала разыскиваем старшие степени:

И записываем соответствующие коэффициенты в первое уравнение системы:

Хорошо запомните следующий нюанс . Что было бы, если б в правой части вообще не было ? Скажем, красовалось бы просто без всякого квадрата? В этом случае в уравнении системы нужно было бы поставить справа ноль: . Почему ноль? А потому что в правой части всегда можно приписать этот самый квадрат с нулём: Если в правой части отсутствуют какие-нибудь переменные или (и) свободный член, то в правых частях соответствующих уравнений системы ставим нули .

Записываем соответствующие коэффициенты во второе уравнение системы:

И, наконец, минералка, подбираем свободные члены.

Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент сказала, что разбросает члены по числовой прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.

Система готова:

Решаем систему:

(1) Из первого уравнения выражаем и подставляем его во 2-е и 3-е уравнения системы. На самом деле можно было выразить (или другую букву) из другого уравнения, но в данном случае выгодно выразить именно из 1-го уравнения, поскольку там самые маленькие коэффициенты .

(2) Приводим подобные слагаемые во 2-м и 3-м уравнениях.

(3) Почленно складываем 2-е и 3-е уравнение, при этом, получая равенство , из которого следует, что

(4) Подставляем во второе (или третье) уравнение, откуда находим, что

(5) Подставляем и в первое уравнение, получая .

Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений?

После решения системы всегда полезно сделать проверку – подставить найденные значения в каждое уравнение системы, в результате всё должно «сойтись».

Почти приехали. Коэффициенты найдены, при этом:

Чистовое оформление задание должно выглядеть примерно так:

Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле .

Проверка: Дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.
В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно. Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия .

Пример 2

Найти неопределенный интеграл.

Вернемся к дроби из первого примера: . Нетрудно заметить, что в знаменателе все множители РАЗНЫЕ. Возникает вопрос, а что делать, если дана, например, такая дробь: ? Здесь в знаменателе у нас степени, или, по-математически кратные множители . Кроме того, есть неразложимый на множители квадратный трехчлен (легко убедиться, что дискриминант уравнения отрицателен, поэтому на множители трехчлен никак не разложить). Что делать? Разложение в сумму элементарных дробей будет выглядеть наподобие с неизвестными коэффициентами вверху или как-то по-другому?

Пример 3

Представить функцию

Шаг 1. Проверяем, правильная ли у нас дробь
Старшая степень числителя: 2
Старшая степень знаменателя: 8
, значит, дробь является правильной.

Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Очевидно, что нет, всё уже разложено. Квадратный трехчлен не раскладывается в произведение по указанным выше причинам. Гуд. Работы меньше.

Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей.
В данном случае, разложение имеет следующий вид:

Смотрим на наш знаменатель:
При разложении дробно-рациональной функции в сумму элементарных дробей можно выделить три принципиальных момента:

1) Если в знаменателе находится «одинокий» множитель в первой степени (в нашем случае ), то вверху ставим неопределенный коэффициент (в нашем случае ). Примеры №1,2 состояли только из таких «одиноких» множителей.

2) Если в знаменателе есть кратный множитель , то раскладывать нужно так:
– то есть последовательно перебрать все степени «икса» от первой до энной степени. В нашем примере два кратных множителя: и , еще раз взгляните на приведенное мной разложение и убедитесь, что они разложены именно по этому правилу.

3) Если в знаменателе находится неразложимый многочлен второй степени (в нашем случае ), то при разложении в числителе нужно записать линейную функцию с неопределенными коэффициентами (в нашем случае с неопределенными коэффициентами и ).

На самом деле, есть еще 4-й случай, но о нём я умолчу, поскольку на практике он встречается крайне редко.

Пример 4

Представить функцию в виде суммы элементарных дробей с неизвестными коэффициентами.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Строго следуйте алгоритму!

Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа.

Пример 5

Найти неопределенный интеграл.

Шаг 1. Очевидно, что дробь является правильной:

Шаг 2. Можно ли что-нибудь разложить в знаменателе на множители? Можно. Здесь сумма кубов . Раскладываем знаменатель на множители, используя формулу сокращенного умножения

Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Обратите внимание, что многочлен неразложим на множители (проверьте, что дискриминант отрицательный), поэтому вверху мы ставим линейную функцию с неизвестными коэффициентами, а не просто одну буковку.

Приводим дробь к общему знаменателю:

Составим и решим систему:

(1) Из первого уравнения выражаем и подставляем во второе уравнение системы (это наиболее рациональный способ).

(2) Приводим подобные слагаемые во втором уравнении.

(3) Почленно складываем второе и третье уравнения системы.

Все дальнейшие расчеты, в принципе, устные, так как система несложная.

(1) Записываем сумму дробей в соответствии с найденными коэффициентами .

(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урока Интегрирование некоторых дробей .

(3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей ).

(4) Берём второй интеграл, в третьем – выделяем полный квадрат.

(5) Берём третий интеграл. Готово.