Пусть имеется некоторая система, состояние которой однозначно характеризуется определенным набором величин, как правило, недоступных для измерения (аектор состояния системы).
Имеется ряд переменных. Некоторым образом, связанных с состоянием системы, которую можно измерить с заданной точностью. Алгоритм фильтра Калмана позволяет в реальном времени построить реальную оценку состояния системы, основываясь на измерениях, содержащих погрешности. Вектор измерений рассматривается в качестве многомерного выходного сигнала системы, при этом зашумленного, вектор состояния – неизвестный многомерный сигнал, подлежащий определению условием оптимальности построенной оценки является min ее средне – кв. ошибки.
Особенности фильтра Калмана:
Позволяет получит решение задачи, сформулированной в пр……………сост
Фильтр является не стационарным
Имеет рекурентную форму, то есть удобен для программирования. Новые оценки получаются корректировкой старых на основе новых наблюдений.
В общем случае задано п – мерное гильбертово пр – во.
Задан процесс, формируемый линейной динамичной системой, названной формирующим фильтром
Dx/dt =A(t) x(t) +B(t)u(t)+V(t)
X(t) - случайный п – мерный процесс.
- U(t) - c куч. процесс в виде б.ш.с ковариационной матрицей
K u (t , M (t) (t- )
Х(t) наблюдается с помощью измерителя:
Y(t) = c(t)x(t) +n(t)
n(t)
=
Б.Ш.
K n (t , ) = M=R(t) (t- )
Основываясь на наблюдениях у в течение интервала времени , нужно найти оценку сигнала x(t) tx(t))
x
 (t)=x(t)
– x(t)
-
ошибка оценивания
(t)=x(t)
– x(t)
-
ошибка оценивания
Критерием оптимальности является ее кв. Форма
//X (t)
//
2
min
(t)
//
2
min
Процессы u(t) иx(t) иV(t) и n(t) не коррелированы, а формирующий фильтр удовлетворяет условиям физической реализуемости.
U(t) x(t) x(t)
x(t) x(t) n(t)
n(t)
Фф – формирующий фильтр
u
U(t) y(t)
L

x(t) x(t)
Динамические свойства системы зависят от L, выбор L обеспечивает
X(t) – x(t) o
t
Начальные условия на каждом новом цикле алгоритма служит оценка состояния системы и величина характеризует ее погрешность.
Алгоритм последовательно обрабатывает вновь поступающие векторы измерений, учитывая при этом значении, выч. на предыдущем цикле. На сп. Шаге, с обрабат измерений, уточняются н.у. для этого алгоритма выч. без поправок к ним на основе ковареац.матриц. Исправленные т.о. н.у. и являются выходными данными фильтра Калмана на каждом цикле. На заключительном этапе алгоритма происходит подготовка к поступлению нового вектора измерений. На основе заданного линейного преобразования, связывая его последующий вектор состояния с предыдущим, прогнозируется оценка состояния системы в момент следующее измерение.
Рассмотрим многомерный фильтр Калмана для стационарного случая. Должно быт известно само описание объекта:
X(K+1) = Ax(K)+Bu(K)+V(k)
Y(K) = cx(K0+n(K)
A 1 B 1 C=const (стационарный случай)
Должна быть известна априорная информация о сигнале:
M[x] =x o u cov [x] = o
Должна быть известна априорная информация о шуме, то есть Р (v) – гаусовская плотность M[v]=o ; cov[V]=V
P(n) M[n]=o ; cov[n]=N
V - шум объекта; n - шум измерения
Алгоритм работы фильтра Калмана:
X(K+1) = Ax(k)+Bu(k)+L(K+1)
Каждая оценка получается на основании предыдущего x(K) и на основании текущего измерения y(u+1) ; предсказывает текущую выборку – Ax(u)+Bu(K) - экстраполир.состояние.
L Cbu(K) корректирует текущую оценку на основании оценки ошибки
C - новизна между наблюдавшимся и предсказанным значением.
L(K+1) - изменяющийся во времени коэффициент Калмана.
L= KoC 1 p -1 p - матрица самого сигнала; Ko - единственное положительно определенное решение алгебраичного матричного уравнения (уравнение Реккати)
Этот идентификатор должен быть устойчив, то есть собственное значение матрицы имеет «-« вещественную часть.
Уравнение фильтра Калмана однозначно определяет все коэффициенты идентификатора по данным о характерах помех в соответствии с выбором критерия min CK погрешности.
Запишем рекурентную форму:
L(K+1) = (K+1) c 1 -1 = P(K+1)C 1 N -1
(K+1) = AP(K)A 1 +V
P(K+1)= [ -1 (K+1)>C 1 N -1 C] -1 = (K+1)- (K+1)C 1 -1 c (k+1)
(K+1)- априорное значение ковариац.матрицы сигнала x , основанное на k наблюдениях.
Сначала вычисляется:
1. (k+1)
2. P(k+1)
3. L(k+1)
4. x(k+1)
Пример:
 упрощенный т.к.: априорный случай
(скамерный фильтр Калмана); и с=1
упрощенный т.к.: априорный случай
(скамерный фильтр Калмана); и с=1
Рассматривание стационарных случайных сигнал x(k) с известными статистическими характерами, искажается стац.б.ш. max / наилучшим образом оценить х(и)
X(k+1) = ax(k) +v(k)
Y(k) = x(k)+n(k)
X(o)= x o P(o)=P o
M[v]=o M=V ij
M[k]=o M=N ij
M=O
x^(n+1)=ax(k)+L(k+1)
l(k+1)= (k+1)[ (k+1)+N] -1 = (k+1)/ (k+1)+N
(k+1)=AP(k)A 1 +V=a 2 P(k)+v
P(k+1)=[ -1 (k+1)+N -1 ] -1 = (k+1)N/ (k+1)+N
X(k+1)=(1-l(k+1))ax(k)+l(k+1)y(k+1)=N
 /
(k+1)+N
ax(k)+
(k+1)/
(k+1)+N
y(k+1)
/
(k+1)+N
ax(k)+
(k+1)/
(k+1)+N
y(k+1)
L


L(k+1)+ (k+1)=1
Предположим, что есть априорная информация:
X
o
=o
P
o
=o
N=V
=
|
K (k) l(k) P(k) |
1 N 0,5 0,5N
2 1 ,25 N 0 ,555 0,555 N
3 1 ,28 N 0,56 0,56N
4 1 ,28 N 0,56 0,56N
x
o
=o
P
o
=
N=V a=
k (k) l(k) P(k)
o
1 1 N
2 1 ,5 N 0 ,6 0,6 N
3 1,3N 0 ,565 0,565 N
4 1 ,283 N 0 ,56 0,565 N
5 1 ,28 N 0 ,56 0,56 N
0 ,56 N
P(k) =P(k-1)=P - условие стационарности фильтра
Р = N/ +N =(a 2 P+V)N/ a 2 P +N+V
(a 2 P +V)N =PN+P(a 2 P+V)
P 2 + N+V-a 2 N/a 2 P – VN/a 2 =O
P 2 +3Np – 2N 2 =O
P = 0 ,56 N
Коэффициент усиления L не зависит от наблюдений и может быть вычислен заранее для всей процедуры.
Зависимость от времени матриц A , B , С не вносит принципиальных изменений (когда эти матрицы полностью известны)
Фильтр Калмана реализует процесс паралистического оценивания.
При порциальном распределении случайных величин в стационарном случае рассматриваемый фильтр оптимален, в смысле метода полим. Квадратов, если система не стационарна, то фильтр оптимален.
Одновременное оценивание параметров и состояние объекта
Рассматривая задачу оценки состояний, когда известна лишь структура матрицы объекта, то есть известны функции, которые содержат матрицы, и не известны значения параметров, которые содержат сами функции. Прямой подход к решению такой задачи предполагает расширение вектора состояний за счет неизвестных параметров.
U(t) x 1 (t)
 Y
1
(t)
Y
1
(t)
 Y
2
(t)
Y
2
(t)
Необходимо оценить состояние х и среднее значение помехи п по доступным наблюдениям сигналов у 1 и у 2 при этом а неизвестен.
Составим расширенный вектор состояния, который мы будем определять:
X 1 (t) x 1 (t)
X(t)= a = x 2 (t)
N x 3 (t)
A=n=o (так как не являются фильтрами времени)
X 1 (t)/u(t) = 1/a+s x 1 o (t) = -x 1 (t)x 2 (t)+u(t)
X 1 (t) = u(t)/a+s
X 1 (t)(a+s)= u(t) x 1 x 2 +sx 1 =u
Для вектора состояния записать уравнение связи x(t) и u(t) невозможно.
X = A(x(t)+B(x(t),t) u(t)
-x 1 +x 2 (t) 1
A = o B = o
Рассмотрим вектор наблюдений
Y(t) =c(x(t) , t) + v(t)
C(x(t) , t) =
V(t) =
Пусть объект описывается
X = j (x,u , a , v , t)
Y = g(x,u ,с, n , t)
X (x ,u, a , v , t)
[x/a ] нельзя преобразовать к M - линейная форма, где М не зависит от х и а .
Даже для линейного объекта задача совместная.
Оценивание параметров и состояний относительно этого вектора параметров и состояния. Все подходы должны осуществляться на основе настраивания модели и иметь итеративный характер.
Рассмотрим на основании выборочных сигналов:
X(k+1) = t(x(k), u(k) , a(k), v(k), k)
Y9k) = g(x(k) , n(k) ,с(k ), n(k) , k)
Используется нелинейный нестационарный объект
(x(k), u(k) , a(k), k) + G(k)V(k)g(x(k)u(k)c(k)k)+n(k)
(шум объекта аддитивный) (шум наблюдений аддетивный)
A(k)x(k) +B(k)u(k) c(k)x(k)+D(k)u(k)
(линейный объект) наблюдаемое линейно-относительных переменных состояний
Ax(k)+Bu(k) cx(k) + Du(k)
(стационарный объект) матрица наблюдений постоянная)
(k)=o
В таком виде задача называется двухточечной.
Идентификация нелинейных объектов
Тип нелинейности Гаммерштейна.
Эта модель опирается на предположение, что нелинейность и динамику можно разделить. Это можно представить в виде последовательных комбинаций 2х звеньев: нелинейного инерционного и динамического линейного.
U(t) y(t)
Y(t)
=
 d
d
В одномерном сигнале надо идентифицировать 2 функции. Эти функции представляются в виде разложения по некоторым заданным системой функциям.
(u)=
aj
 j
(u)
;
w(t) =
b
i
w
i
(t)
j
(u)
;
w(t) =
b
i
w
i
(t)
j=1 i=1
Введем следующие обозначения:
Y
ij
(t)
= i
(
)
i
(
) j
[
j
]=
a
[
i
][
j
];
j
[
j
]=
a
[
i
][
j
];
}
}
для (int
i
= 0;
i
< 6;
i
++){
для (int
j
= 0;
j
< 3;
j
++){
B
[
i
][
j
]=
b
[
i
][
j
];
}
}
/*
инициализирует состояние*/
state=0.1;
state=0.1;
state=0.1;
state=0.1;
state=0.1;
state=0.1;
lastState= состояние ;
пустой
kalman(){
lastState=
состояние
;
state=c_a1;
state=c_a2;
state=c_a3;
state=a1d;
state=a2d;
state=a3d;
measurement=m_a1;
measurement=m_a2;
measurement=m_a3;
measurement=a1d;
measurement=a2d;
measurement=a3d;
action=tau1;
action=tau2;
action=tau3;
matrix temp1(6,6);
matrix temp2(6,6);
matrix temp3(6,6);
matrix temp4(6,1);
/************ Уравнения
п
рогнозировани
я
*****************/
x = A*lastState + B*action;
p = A*P*A’ + Q;
/************ Уравнения обновления **********/
K = p*C*pinv(C*p*C’+R);
y=C*state;
состояние = x + K*(y-C*lastState);
P = (eye(6) – K*C)*p;
a1=state;
a2=state;
a3=state;
a1d=state;
a2d=state;
a3d=state;
}
/* Эта функция не используется, так как я использую позиции, чтобы получить скорости (т.е. дифференциацию).
* Тем не менее я считаю, что это полезно включить, если вы хотите скорости и позицию
* от ускорения вы будете использовать его */
пустой
integrate(){
new_a1d = a1d + a1dd*TIMESTEP;
a1 += (new_a1d + a1d)*TIMESTEP/2;
a1d = new_a1d;
new_a2d = a2d + a2dd*TIMESTEP;
a2 += (new_a2d + a2d)*TIMESTEP/2;
a2d = new_a2d;
new_a3d = a3d + a3dd*TIMESTEP;
a3 += (new_a3d + a3d)*TIMESTEP/2;
a3d = new_a3d;
TIME+=TIMESTEP;
}
/*Это дает мне скорость от позиции*/
пустой
differentiation(){
a1d=(state-lastState)/TIMESTEP;
a2d=(state-lastState)/TIMESTEP;
a3d=(state-lastState)/TIMESTEP;
TIME+=TIMESTEP;
}
int main () {
initKalman();
char buffer;
ifstream readFile (“DATA.txt”); // вот тут я читал мои данные, так как я обрабатывал все это оффлайн
while (!readFile.eof()){
readFile.getline (buffer,500);
sscanf(buffer, “%f %f %f %f %f %f %f %f %f %f “,&timeIndex,&m_a1,&m_a2,&m_a3,&c_a1,&c_a2,&c_a3,&tau1,&tau2,&tau3);
kalman();
differentiation();
//integrate();
/*
вот тут я вношу в журнал результаты и / или выношу их на экран */
FILE *file=fopen(“filterOutput.txt”, “a”);
fprintf(file,”%f %f %f %f %f %f %f %f %f %f \n”,TIME,a1,a2,a3,a1d,a2d,a3d,tau1,tau2,tau3);
fprintf(stderr,”%f %f %f %f %f %f %f %f %f %f \n”,TIME,a1,a2,a3,a1d,a2d,a3d,tau1,tau2,tau3);
fclose(file);
}
return 1;
}
Заключение
Этот пост был сосредоточен на реализации фильтра Калмана. Надеюсь, вы сможете принять эту информацию, чтобы улучшить и усовершенствовать ваши робототехнические проекты. Для получения дополнительной информации я рекомендую Введение в фильтрацию Калмана Грега Уэлча и Гэри Бишопа http://www.cs.unc.edu/~welch/kalman/ и пост из TKJ Electronics .
Фильтр Калмана широко используется в инженерных и эконометрических приложениях: от радаров и систем технического зрения до оценок параметров макроэкономических моделей . Калмановская фильтрация является важной частью теории управления , играет большую роль в создании систем управления. Совместно с линейно-квадратичным регулятором фильтр Калмана позволяет решить задачу линейно-квадратичного гауссовского управления . Фильтр Калмана и линейно-квадратичный регулятор - возможное решение большинства фундаментальных задач в теории управления.
В большинстве приложений количество параметров, задающих состояние объекта, больше, чем количество наблюдаемых параметров, доступных для измерения. При помощи модели объекта по ряду доступных измерений фильтр Калмана позволяет получить оценку внутреннего состояния.
Фильтр Калмана предназначен для рекурсивного дооценивания вектора состояния априорно известной динамической системы, то есть для расчёта текущего состояния системы необходимо знать текущее измерение, а также предыдущее состояние самого фильтра. Таким образом, фильтр Калмана, как и множество других рекурсивных фильтров, реализован во временно́м, а не в частотном представлении.
Наглядный пример возможностей фильтра - получение точных, непрерывно обновляемых оценок положения и скорости некоторого объекта по результатам временно́го ряда неточных измерений его местоположения. Например, в радиолокации стоит задача сопровождения цели, определения её местоположения, скорости и ускорения, при этом результаты измерений поступают постепенно и сильно зашумлены. Фильтр Калмана использует вероятностную модель динамики цели, задающую тип вероятного движения объекта, что позволяет снизить воздействие шума и получить хорошие оценки положения объекта в настоящий, будущий или прошедший момент времени.
Введение
Фильтр Калмана оперирует понятием вектора состояния системы (набором параметров, описывающих состояние системы на некоторый момент времени) и его статистическим описанием. В общем случае динамика некоторого вектора состояния описывается плотностями вероятности распределения его компонент в каждый момент времени. При наличии определенной математической модели производимых наблюдений за системой, а также модели априорного изменения параметров вектора состояния (а именно - в качестве марковского формирующего процесса) можно записать уравнение для апостериорной плотности вероятности вектора состояния в любой момент времени. Данное дифференциальное уравнение носит название уравнение Стратоновича . Уравнение Стратоновича в общем виде не решается. Аналитическое решение удается получить только в случае ряда ограничений (предположений):
- гауссовости априорных и апостериорных плотностей вероятности вектора состояния на любой момент времени (в том числе начальный)
- гауссовости формирующих шумов
- гауссовости шумов наблюдений
- белости шумов наблюдений
- линейности модели наблюдений
- линейности модели формирующего процесса (который, напомним, должен являться марковским процессом)
Классический фильтр Калмана является уравнениями для расчета первого и второго момента апостериорной плотности вероятности (в смысле вектора математических ожиданий и матрицы дисперсий, в том числе взаимных) при данных ограничениях. Ввиду того, что для нормальной плотности вероятности математическое ожидание и дисперсионная матрица полностью задают плотность вероятности, можно сказать, что фильтр Калмана рассчитывает апостериорную плотность вероятности вектора состояния на каждый момент времени. А значит полностью описывает вектор состояния как случайную векторную величину.
Расчетные значения математических ожиданий при этом являются оптимальными оценками по критерию среднеквадратической ошибки, что и обуславливает его широкое применение.
Существует несколько разновидностей фильтра Калмана, отличающихся приближениями и ухищрениями, которые приходится применять для сведения фильтра к описанному виду и уменьшения его размерности:
- Расширенный фильтр Калмана (EKF, Extended Kalman filter). Сведение нелинейных моделей наблюдений и формирующего процесса с помощью линеаризации посредством разложения в ряд Тейлора .
- Unscented Kalman filter (UKF). Используется в задачах, в которых простая линеаризация приводит к уничтожению полезных связей между компонентами вектора состояния. В этом случае «линеаризация» основана на unscented -преобразовании.
- Ensemble Kalman filter (EnKF). Используется для уменьшения размерности задачи.
- Возможны варианты с нелинейным дополнительным фильтром, позволяющим привести негауссовские наблюдения к нормальным.
- Возможны варианты с «обеляющим» фильтром, позволяющим работать с «цветными» шумами
- и т. д.
Используемая модель динамической системы
Фильтры Калмана базируются на дискретизированных по времени линейных динамических системах . Такие системы моделируются цепями Маркова при помощи линейных операторов и слагаемых с нормальным распределением . Состояние системы описывается вектором конечной размерности - вектором состояния . В каждый такт времени линейный оператор действует на вектор состояния и переводит его в другой вектор состояния (детерминированное изменение состояния), добавляется некоторый вектор нормального шума (случайные факторы) и в общем случае вектор управления, моделирующий воздействие системы управления. Фильтр Калмана можно рассматривать как аналог скрытым моделям Маркова , с тем отличием, что переменные, описывающие состояние системы, являются элементами бесконечного множества действительных чисел (в отличие от конечного множества пространства состояний в скрытых моделях Маркова). Кроме того, скрытые модели Маркова могут использовать произвольные распределения для последующих значений вектора состояния, в отличие от фильтра Калмана, использующего модель нормально распределенного шума. Существует строгая взаимосвязь между уравнениями фильтра Калмана и скрытой модели Маркова. Обзор этих и других моделей дан Roweis и Chahramani (1999) .
При использовании фильтра Калмана для получения оценок вектора состояния процесса по серии зашумленных измерений необходимо представить модель данного процесса в соответствии со структурой фильтра - в виде матричного уравнения определенного типа. Для каждого такта k работы фильтра необходимо в соответствии с приведенным ниже описанием определить матрицы: эволюции процесса F k ; матрицу наблюдений H k ; ковариационную матрицу процесса Q k ; ковариационную матрицу шума измерений R k ; при наличии управляющих воздействий - матрицу их коэффициентов B k .
Многие реальные динамические системы нельзя точно описать данной моделью. На практике неучтённая в модели динамика может серьёзно испортить рабочие характеристики фильтра, особенно при работе с неизвестным стохастическим сигналом на входе. Более того, неучтённая в модели динамика может сделать фильтр неустойчивым . С другой стороны, независимый белый шум в качестве сигнала не будет приводить к расхождению алгоритма. Задача отделения шумов измерений от неучтенной в модели динамики сложна, решается она с помощью теории робастных систем управления .
Фильтр Калмана
Фильтр Калмана является разновидностью рекурсивных фильтров . Для вычисления оценки состояния системы на текущий такт работы ему необходима оценка состояния (в виде оценки состояния системы и оценки погрешности определения этого состояния) на предыдущем такте работы и измерения на текущем такте. Данное свойство отличает его от пакетных фильтров, требующих в текущий такт работы знание истории измерений и/или оценок. Далее под записью будем понимать оценку истинного вектора в момент n с учетом измерений с момента начала работы и по момент m включительно.
Состояние фильтра задается двумя переменными:
Итерации фильтра Калмана делятся на две фазы: экстраполяция и коррекция. Во время экстраполяции фильтр получает предварительную оценку состояния системы (в русскоязычной литературе часто обозначается , где означает «экстраполяция», а k - номер такта, на котором она получена) на текущий шаг по итоговой оценке состояния с предыдущего шага (либо предварительную оценку на следующий такт по итоговой оценке текущего шага, в зависимости от интерпретации). Эту предварительную оценку также называют априорной оценкой состояния, так как для её получения не используются наблюдения соответствующего шага. В фазе коррекции априорная экстраполяция дополняется соответствующими текущими измерениями для коррекции оценки. Скорректированная оценка также называется апостериорной оценкой состояния, либо просто оценкой вектора состояния . Обычно эти две фазы чередуются: экстраполяция производится по результатам коррекции до следующего наблюдения, а коррекция производится совместно с доступными на следующем шаге наблюдениями, и т. д. Однако возможно и другое развитие событий, если по некоторой причине наблюдение оказалось недоступным, то этап коррекции может быть пропущен и выполнена экстраполяция по нескорректированной оценке (априорной экстраполяции). Аналогично, если независимые измерения доступны только в отдельные такты работы, всё равно возможны коррекции (обычно с использованием другой матрицы наблюдений H k ).
Этап экстраполяции
| Экстраполяция (предсказание) вектора состояния системы по оценке вектора состояния и примененному вектору управления с шага (k −1 ) на шаг k : | |
| Ковариационная матрица для экстраполированного вектора состояния : |
Этап коррекции
| Отклонение полученного на шаге k наблюдения от наблюдения, ожидаемого при произведенной экстраполяции: | |
| Ковариационная матрица для вектора отклонения (вектора ошибки): | |
| Оптимальная по Калману матрица коэффициентов усиления, формирующаяся на основании ковариационных матриц имеющейся экстраполяции вектора состояния и полученных измерений (посредством ковариационной матрицы вектора отклонения): | |
| Коррекция ранее полученной экстраполяции вектора состояния - получение оценки вектора состояния системы: | |
| Расчет ковариационной матрицы оценки вектора состояния системы: |
Выражение для ковариационной матрицы оценки вектора состояния системы справедливо только при использовании приведенного оптимального вектора коэффициентов. В общем случае это выражение имеет более сложный вид.
Инварианты
Если модель абсолютно точна и абсолютно точно заданы начальные условия и , то следующие величины сохраняются после любого количества итераций работы фильтра - являются инвариантами:
Математические ожидания оценок и экстраполяций вектора состояния системы, матрицы ошибок являются нуль-векторами:
где - математическое ожидание .
Расчетные матрицы ковариаций экстраполяций, оценок состояния системы и вектора ошибок совпадают с истинными матрицами ковариаций:
Пример построения фильтра
Представим себе вагонетку , стоящую на бесконечно длинных рельсах при отсутствующем трении . Изначально она покоится в позиции 0, но под действием случайных факторов на неё действует случайное ускорение . Мы измеряем положение вагонетки каждые ∆t секунд, но измерения неточны. Мы хотим получать оценки положения вагонетки и её скорости. Применим к этой задаче фильтр Калмана, определим все необходимые матрицы.
В данной задаче матрицы F , H , R и Q не зависят от времени, опустим их индексы. Кроме того, мы не управляем вагонеткой, поэтому матрица управления B отсутствует.
Координата и скорость вагонетки описывается вектором в линейном пространстве состояний
где - скорость (первая производная координаты по времени).
Будем считать, что между (k −1 )-ым и k -ым тактами вагонетка движется с постоянным ускорением a k , распределенным по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением σ a . В соответствии с механикой Ньютона можно записать
Ковариационная матрица случайных воздействий
(σ a - скаляр).На каждом такте работы производится измерение положения вагонетки. Предположим, что погрешность измерений v k имеет нормальное распределение с нулевым математическим ожиданием и среднеквадратическим отклонением σ z . Тогда
и ковариационная матрица шума наблюдений имеет вид
.Начальное положение вагонетки известно точно
,Если же положение и скорость вагонетки известна лишь приблизительно, то можно инициализировать матрицу дисперсий достаточно большим числом L , чтобы при этом число превосходило дисперсию измерений координаты
,В этом случае на первых тактах работы фильтр будет с бо́льшим весом использовать результаты измерений, чем имеющуюся априорную информацию.
Вывод формул
Ковариационная матрица оценки вектора состояния
По определению ковариационной матрицы P k |k
подставляем выражение для оценки вектора состояния
и расписываем выражение для вектора ошибок
и вектора измерений
выносим вектор погрешности измерений v k
так как вектор погрешности измерений v k не коррелирован с другими аргументами, получаем выражение
в соответствии со свойствами ковариации векторов данное выражение преобразуется к виду
заменяя выражение для ковариационной матрицы экстраполяции вектора состояния на P k |k −1 и определение ковариационной матрицы шумов наблюдений на R k , получаем
Полученное выражение справедливо для произвольной матрицы коэффициентов, но если в качестве неё выступает матрица коэффициентов, оптимальная по Калману, то данное выражение для ковариационной матрицы можно упростить.
Оптимальная матрица коэффициентов усиления
Фильтр Калмана минимизирует сумму квадратов математических ожиданий ошибок оценки вектора состояния.
Вектор ошибки оценки вектора состояния
Стоит задача минимизировать сумму математических ожиданий квадратов компонент данного вектора
Винеровские фильтры лучше всего подходят для обработки процессов или отрезков процессов в целом (блочная обработка). Для последовательной обработки требуется текущая оценка сигнала на каждом такте с учетом информации, поступающей на вход фильтра в процессе наблюдения.
При винеровской фильтрации каждый новый отсчет сигнала потребовал бы пересчета всех весовых коэффициентов фильтра. В настоящее время широкое распространение получили адаптивные фильтры, в которых поступающая новая информация используется для непрерывной корректировки ранее сделанной оценки сигнала (сопровождение цели в радиолокации, системы автоматического регулирования в управлении и т.д). Особенный интерес представляют адаптивные фильтры рекурсивного типа, известные как фильтр Калмана.
Эти фильтры широко используются в контурах управления в системах автоматического регулирования и управления. Именно оттуда они и появились, подтверждением чему служит столь специфическая терминология, используемая при описании их работы, как пространство состояний.
Одна из основных задач, требующих своего решения в практике нейронных вычислений, – получение быстрых и надежных алгоритмов обучения НС. В этой связи может оказаться полезным использование в контуре обратной связи обучающего алгоритма линейных фильтров. Так как обучающие алгоритмы имеют итеративную природу, такой фильтр должен представлять собой последовательное рекурсивное устройство оценки.
Задача оценки параметров
Одной из задач теории статистических решений, имеющих большое практическое значение, является задача оценки векторов состояния и параметров систем, которая формулируется следующим образом. Предположим, необходимо оценить значение векторного параметра $X$, недоступного непосредственному измерению. Вместо этого измеряется другой параметр $Z$, зависящий от $X$. Задача оценивания состоит в ответе на вопрос: что можно сказать об $X$, зная $Z$. В общем случае, процедура оптимальной оценки вектора $X$ зависит от принятого критерия качества оценки.
Например, байесовский подход к задаче оценки параметров требует полной априорной информации о вероятностных свойствах оцениваемого параметра, что зачастую невозможно. В этих случаях прибегают к методу наименьших квадратов (МНК), который требует значительно меньше априорной информации.
Рассмотрим применения МНК для случая, когда вектор наблюдения $Z$ связан с вектором оценки параметров $X$ линейной моделью, и в наблюдении присутствует помеха $V$, некоррелированная с оцениваемым параметром:
$Z = HX + V$, (1)
где $H$ – матрица преобразования, описывающая связь наблюдаемых величин с оцениваемыми параметрами.
Оценка $X$, минимизирующая квадрат ошибки, записывается следующим образом:
$X_{оц}=(H^TR_V^{-1}H)^{-1}H^TR_V^{-1}Z$, (2)
Пусть помеха $V$ не коррелирована, в этом случае матрица $R_V$ есть просто единичная матрица, и уравнение для оценки становится проще:
$X_{оц}=(H^TH)^{-1}H^TZ$, (3)
Запись в матричной форме сильно экономит бумагу, но может быть для кого то непривычна. Следующий пример, взятый из монографии Коршунова Ю. М. "Математические основы кибернетики", все это иллюстрирует.
Имеется следующая электрическая цепь:
Наблюдаемые величины в данном случае – показания приборов $A_1 = 1 A, A_2 = 2 A, V = 20 B$.
Кроме того, известно сопротивление $R = 5$ Ом. Требуется оценить наилучшим образом, с точки зрения критерия минимума среднего квадрата ошибки значения токов $I_1$ и $I_2$. Самое важное здесь заключается в том, что между наблюдаемыми величинами (показаниями приборов) и оцениваемыми параметрами существует некоторая связь. И эта информация привносится извне.
В данном случае, это законы Кирхгофа, в случае фильтрации (о чем речь пойдет дальше) – авторегрессионная модель временного ряда, предполагающая зависимость текущего значения от предшествующих.
Итак, знание законов Кирхгофа, никак не связанное с теорией статистических решений, позволяет установить связь между наблюдаемыми значениями и оцениваемыми параметрами (кто изучал электротехнику – могут проверить, остальным придется поверить на слово):
$$z_1 = A_1 = I_1 + \xi_1 = 1$$
$$z_2 = A_2 = I_1 + I_2 + \xi_2 = 2$$
$$z_2 = V/R = I_1 + 2 * I_2 + \xi_3 = 4$$
Это же в векторной форме:
$$\begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} \begin{vmatrix} I_1\\ I_2 \end{vmatrix} + \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$
Или $Z = HX + V$, где
$$Z= \begin{vmatrix} z_1\\ z_2\\ z_3 \end{vmatrix} = \begin{vmatrix} 1\\ 2\\ 4 \end{vmatrix} ; H= \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} ; X= \begin{vmatrix} I_1\\ I_2 \end{vmatrix} ; V= \begin{vmatrix} \xi_1\\ \xi_2\\ \xi_3 \end{vmatrix}$$
Считая значения помехи некоррелированными между собой, найдем оценку I 1 и I 2 по методу наименьших квадратов в соответствии с формулой 3:
$H^TH= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 & 0\\ 1 & 1\\ 1 & 2 \end{vmatrix} = \begin{vmatrix} 3 & 3\\ 3 & 5 \end{vmatrix} ; (H^TH)^{-1}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} $;
$H^TZ= \begin{vmatrix} 1 & 1& 1\\ 0 & 1& 2 \end{vmatrix} \begin{vmatrix} 1 \\ 2\\ 4 \end{vmatrix} = \begin{vmatrix} 7\\ 10 \end{vmatrix} ; X{оц}= \frac{1}{6} \begin{vmatrix} 5 & -3\\ -3 & 3 \end{vmatrix} \begin{vmatrix} 7\\ 10 \end{vmatrix} = \frac{1}{6} \begin{vmatrix} 5\\ 9 \end{vmatrix}$;
Итак $I_1 = 5/6 = 0,833 A$; $I_2 = 9/6 = 1,5 A$.
Задача фильтрации
В отличие от задачи оценки параметров, которые имеют фиксированные значения, в задаче фильтрации требуется оценивать процессы, то есть находить текущие оценки изменяющегося во времени сигнала, искаженного помехой, и, в силу этого, недоступного непосредственному измерению. В общем случае вид алгоритмов фильтрации зависит от статистических свойств сигнала и помехи.
Будем предполагать, что полезный сигнал – медленно меняющаяся функция времени, а помеха – некоррелированный шум. Будем использовать метод наименьших квадратов, опять же по причине отсутствия априорных сведений о вероятностных характеристиках сигнала и помехи.
Вначале получим оценку текущего значения $x_n$ по имеющимся $k$ последним значениям временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$. Модель наблюдения та же, что и в задаче оценки параметров:
Понятно, что $Z$ – это вектор–столбец, состоящий из наблюдаемых значений временного ряда $z_n, z_{n-1},z_{n-2}\dots z_{n-(k-1)}$, $V$ – вектор–столбец помехи $\xi _n, \xi _{n-1},\xi_{n-2}\dots \xi_{n-(k-1)}$, искажающий истинный сигнал. А что означают символы $H$ и $X$? О каком, например, векторе–столбце $X$ может идти речь, если все, что необходимо, – это дать оценку текущего значения временного ряда? А что понимать под матрицей преобразований $H$, вообще непонятно.
На все эти вопросы можно ответить только при условии введения в рассмотрение понятия модели генерации сигнала. То есть, необходима некоторая модель исходного сигнала. Это и понятно, при отсутствии априорной информации о вероятностных характеристиках сигнала и помехи остается только строить предположения. Можно назвать это гаданием на кофейной гуще, но специалисты предпочитают другую терминологию. На их "фене" это называется параметрическая модель.
В данном случае оцениваются параметры именно этой модели. При выборе подходящей модели генерации сигнала вспомним о том, что любую аналитическую функцию можно разложить в ряд Тейлора. Поразительное свойство ряда Тейлора заключается в том, что форма функции на любом конечном расстоянии $t$ от некой точки $x=a$ однозначно определяется поведением функции в бесконечно малой окрестности точки $x=a$ (речь идет о ее производных первого и высшего порядков).
Таким образом, существование рядов Тейлора означает, что аналитическая функция обладает внутренней структурой с очень сильной связью. Если, например, ограничиться тремя членами ряда Тейлора, то модель генерации сигнала будет выглядеть так:
$x_{n-i} = F_{-i}x_n$, (4)
$$X_n= \begin{vmatrix} x_n\\ x"_n\\ x""_n \end{vmatrix} ; F_{-i}= \begin{vmatrix} 1 & -i & i^2/2\\ 0 & 1 & -i\\ 0 & 0 & 1 \end{vmatrix} $$
То есть формула 4, при заданном порядке полинома (в примере он равен 2) устанавливает связь между $n$-ым значением сигнала во временной последовательности и $(n-i)$–ым. Таким образом, оцениваемый вектор состояния в данном случае включает в себя, помимо собственно оцениваемого значения, первую и вторую производную сигнала.
В теории автоматического управления такой фильтр назвали бы фильтром с астатизмом 2-го порядка. Матрица преобразования $H$ для данного случая (оценка осуществляется по текущему и $k-1$ предшествующим выборкам) выглядит так:
$$H= \begin{vmatrix} 1 & -k & k^2/2\\ - & - & -\\ 1 & -2 & 2\\ 1 & -1 & 0.5\\ 1 & 0 & 0 \end{vmatrix}$$
Все эти числа получаются из ряда Тейлора в предположении, что временной интервал между соседними наблюдаемыми значениями постоянный и равен 1.
Итак, задача фильтрации при принятых нами предположениях свелась к задаче оценки параметров; в данном случае оцениваются параметры принятой нами модели генерации сигнала. И оценка значений вектора состояния $X$ осуществляется по той же формуле 3:
$$X_{оц}=(H^TH)^{-1}H^TZ$$
По сути, мы реализовали процесс параметрического оценивания, основанный на авторегрессионной модели процесса генерации сигнала.
Формула 3 легко реализуется программно, для этого нужно заполнить матрицу $H$ и вектор столбец наблюдений $Z$. Такие фильтры называются фильтры с конечной памятью , так как для получения текущей оценки $X_{nоц}$ они используют последние $k$ наблюдений. На каждом новом такте наблюдения к текущей совокупности наблюдений прибавляется новое и отбрасывается старое. Такой процесс получения оценок получил название скользящего окна .
Фильтры с растущей памятью
Фильтры с конечной памятью обладают тем основным недостатком, что после каждого нового наблюдения необходимо заново производить полный пересчет по всем хранящимся в памяти данным. Кроме того, вычисление оценок можно начинать только после того, как накоплены результаты первых $k$ наблюдений. То есть эти фильтры обладают большой длительностью переходного процесса.
Чтобы бороться с этим недостатком, необходимо перейти от фильтра с постоянной памятью к фильтру с растущей памятью . В таком фильтре число наблюдаемых значений, по которым производится оценка, должна совпадать с номером n текущего наблюдения. Это позволяет получать оценки, начиная с числа наблюдений, равного числу компонент оцениваемого вектора $X$. А это определяется порядком принятой модели, то есть сколько членов из ряда Тейлора используется в модели.
При этом с ростом n улучшаются сглаживающие свойства фильтра, то есть повышается точность оценок. Однако непосредственная реализация этого подхода связана с возрастанием вычислительных затрат. Поэтому фильтры с растущей памятью реализуются как рекуррентные .
Дело в том, что к моменту n мы уже имеем оценку $X_{(n-1)оц}$, в которой содержится информация обо всех предыдущих наблюдениях $z_n, z_{n-1}, z_{n-2} \dots z_{n-(k-1)}$. Оценку $X_{nоц}$ получаем по очередному наблюдению $z_n$ с использованием информации, хранящейся в оценке $X_{(n-1)}{\mbox {оц}}$. Такая процедура получила название рекуррентной фильтрации и состоит в следующем:
- по оценке $X_{(n-1)}{\mbox {оц}}$ прогнозируют оценку $X_n$ по формуле 4 при $i = 1$: $X_{\mbox {nоцаприори}} = F_1X_{(n-1)оц}$. Это априорная оценка;
- по результатам текущего наблюдения $z_n$, эту априорную оценку превращают в истинную, то есть апостериорную;
- эта процедура повторяется на каждом шаге, начиная с $r+1$, где $r$ – порядок фильтра.
Окончательная формула рекуррентной фильтрации выглядит так:
$X_{(n-1)оц} = X_{\mbox {nоцаприори}} + (H^T_nH_n)^{-1}h^T_0(z_n - h_0 X_{\mbox {nоцаприори}})$, (6)
где для нашего фильтра второго порядка:
Фильтр с растущей памятью, работающий в соответствии с формулой 6 – частный случай алгоритма фильтрации, известного под названием фильтра Калмана.
При практической реализации этой формулы необходимо помнить, что входящая в него априорная оценка определяется по формуле 4, а величина $h_0 X_{\mbox {nоцаприори}}$ представляет собой первую компоненту вектора $X_{\mbox {nоцаприори}}$.
У фильтра с растущей памятью имеется одна важная особенность. Если посмотреть на формулу 6, то окончательная оценка есть сумма прогнозируемого вектора оценки и корректирующего члена. Эта поправка велика при малых $n$ и уменьшается при увеличении $n$, стремясь к нулю при $n \rightarrow \infty$. То есть с ростом n сглаживающие свойства фильтра растут и начинает доминировать модель, заложенная в нем. Но реальный сигнал может соответствовать модели лишь на отдельных участках, поэтому точность прогноза ухудшается.
Чтобы с этим бороться, начиная с некоторого $n$, накладывают запрет на дальнейшее уменьшение поправочного члена. Это эквивалентно изменению полосы фильтра, то есть при малых n фильтр более широкополосен (менее инерционен), при больших – он становится более инерционен.
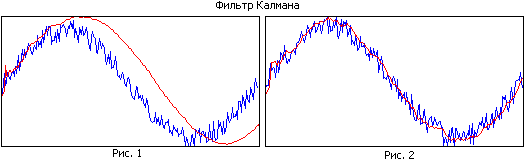
Сравните рисунок 1 и рисунок 2. На первом рисунке фильтр имеет большую память, при этом он хорошо сглаживает, но в силу узкополосности оцениваемая траектория отстает от реальной. На втором рисунке память фильтра меньше, он хуже сглаживает, но лучше отслеживает реальную траекторию.
Литература
- Ю.М.Коршунов "Математические основы кибернетики"
- А.В.Балакришнан "Теория фильтрации Калмана"
- В.Н.Фомин "Рекуррентное оценивание и адаптивная фильтрация"
- К.Ф.Н.Коуэн, П.М. Грант "Адаптивные фильтры"









