Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью -критерия Фишера:
 ,
(2.22)
,
(2.22)
где
 – факторная сумма квадратов на одну
степень свободы;
– факторная сумма квадратов на одну
степень свободы;
 – остаточная сумма квадратов на одну
степень свободы;
– остаточная сумма квадратов на одну
степень свободы;
 – коэффициент (индекс) множественной
детерминации;
– коэффициент (индекс) множественной
детерминации;
 – число параметров при переменных
– число параметров при переменных (в линейной регрессии совпадает с числом
включенных в модель факторов);
(в линейной регрессии совпадает с числом
включенных в модель факторов);
 – число наблюдений.
– число наблюдений.
Оценивается
значимость не только уравнения в целом,
но и фактора, дополнительно включенного
в регрессионную модель. Необходимость
такой оценки связана с тем, что не каждый
фактор, вошедший в модель, может
существенно увеличивать долю объясненной
вариации результативного признака.
Кроме того, при наличии в модели нескольких
факторов они могут вводиться в модель
в разной последовательности. Ввиду
корреляции между факторами значимость
одного и того же фактора может быть
разной в зависимости от последовательности
его введения в модель. Мерой для оценки
включения фактора в модель служит
частный
 -критерий,
т.е.
-критерий,
т.е. .
.
Частный
 -критерий
построен на сравнении прироста факторной
дисперсии, обусловленного влиянием
дополнительно включенного фактора, с
остаточной дисперсией на одну степень
свободы по регрессионной модели в целом.
В общем виде для фактора
-критерий
построен на сравнении прироста факторной
дисперсии, обусловленного влиянием
дополнительно включенного фактора, с
остаточной дисперсией на одну степень
свободы по регрессионной модели в целом.
В общем виде для фактора частный
частный -критерий
определится как
-критерий
определится как
 ,
(2.23)
,
(2.23)
где
 – коэффициент множественной детерминации
для модели с полным набором факторов,
– коэффициент множественной детерминации
для модели с полным набором факторов, – тот же показатель, но без включения
в модель фактора
– тот же показатель, но без включения
в модель фактора ,
, – число наблюдений,
– число наблюдений, – число параметров в модели (без
свободного члена).
– число параметров в модели (без
свободного члена).
Фактическое значение частного
 -критерия
сравнивается с табличным при уровне
значимости
-критерия
сравнивается с табличным при уровне
значимости и числе степеней свободы: 1 и
и числе степеней свободы: 1 и .
Если фактическое значение
.
Если фактическое значение превышает
превышает ,
то дополнительное включение фактора
,
то дополнительное включение фактора в модель статистически оправданно и
коэффициент чистой регрессии
в модель статистически оправданно и
коэффициент чистой регрессии при факторе
при факторе статистически значим. Если же фактическое
значение
статистически значим. Если же фактическое
значение меньше табличного, то дополнительное
включение в модель фактора
меньше табличного, то дополнительное
включение в модель фактора не увеличивает существенно долю
объясненной вариации признака
не увеличивает существенно долю
объясненной вариации признака ,
следовательно, нецелесообразно его
включение в модель; коэффициент регрессии
при данном факторе в этом случае
статистически незначим.
,
следовательно, нецелесообразно его
включение в модель; коэффициент регрессии
при данном факторе в этом случае
статистически незначим.
Для двухфакторного уравнения частные
 -критерии
имеют вид:
-критерии
имеют вид:
 ,
, . (2.23а)
. (2.23а)
С помощью частного
 -критерия
можно проверить значимость всех
коэффициентов регрессии в предположении,
что каждый соответствующий фактор
-критерия
можно проверить значимость всех
коэффициентов регрессии в предположении,
что каждый соответствующий фактор вводился в уравнение множественной
регрессии последним.
вводился в уравнение множественной
регрессии последним.
-Критерий стьюдента для уравнения множественной регрессии.
Частный
 -критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину
-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину ,
можно определить и
,
можно определить и -критерий
для коэффициента регрессии при
-критерий
для коэффициента регрессии при -м
факторе,
-м
факторе, ,
а именно:
,
а именно:
 .
(2.24)
.
(2.24)
Оценка значимости коэффициентов чистой
регрессии по
 -критерию
Стьюдента может быть проведена и без
расчета частных
-критерию
Стьюдента может быть проведена и без
расчета частных -критериев.
В этом случае, как и в парной регрессии,
для каждого фактора используется
формула:
-критериев.
В этом случае, как и в парной регрессии,
для каждого фактора используется
формула:
 ,
(2.25)
,
(2.25)
где
 – коэффициент чистой регрессии при
факторе
– коэффициент чистой регрессии при
факторе ,
, – средняя квадратическая (стандартная)
ошибка коэффициента регрессии
– средняя квадратическая (стандартная)
ошибка коэффициента регрессии .
.
Для уравнения множественной регрессии средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
 ,
(2.26)
,
(2.26)
где

 ,
, – среднее квадратическое отклонение
для признака
– среднее квадратическое отклонение
для признака ,
, – коэффициент детерминации для
уравнения множественной регрессии,
– коэффициент детерминации для
уравнения множественной регрессии, – коэффициент детерминации для
зависимости фактора
– коэффициент детерминации для
зависимости фактора со всеми другими факторами уравнения
множественной регрессии;
со всеми другими факторами уравнения
множественной регрессии; – число степеней свободы для остаточной
суммы квадратов отклонений.
– число степеней свободы для остаточной
суммы квадратов отклонений.
Как видим, чтобы воспользоваться данной
формулой, необходимы матрица межфакторной
корреляции и расчет по ней соответствующих
коэффициентов детерминации
 .
Так, для уравнения
.
Так, для уравнения оценка значимости коэффициентов
регрессии
оценка значимости коэффициентов
регрессии ,
, ,
, предполагает расчет трех межфакторных
коэффициентов детерминации:
предполагает расчет трех межфакторных
коэффициентов детерминации: ,
, ,
, .
.
Взаимосвязь показателей частного
коэффициента корреляции, частного
 -критерия
и
-критерия
и -критерия
Стьюдента для коэффициентов чистой
регрессии может использоваться в
процедуре отбора факторов. Отсев факторов
при построении уравнения регрессии
методом исключения практически можно
осуществлять не только по частным
коэффициентам корреляции, исключая на
каждом шаге фактор с наименьшим незначимым
значением частного коэффициента
корреляции, но и по величинам
-критерия
Стьюдента для коэффициентов чистой
регрессии может использоваться в
процедуре отбора факторов. Отсев факторов
при построении уравнения регрессии
методом исключения практически можно
осуществлять не только по частным
коэффициентам корреляции, исключая на
каждом шаге фактор с наименьшим незначимым
значением частного коэффициента
корреляции, но и по величинам и
и .
Частный
.
Частный -критерий
широко используется и при построении
модели методом включения переменных и
шаговым регрессионным методом.
-критерий
широко используется и при построении
модели методом включения переменных и
шаговым регрессионным методом.
Функция ФИШЕР выполняет возвращение преобразования Фишера для аргументов X . Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Используется функция ФИШЕР для того чтобы проверить гипотезу с помощью коэффициента корреляции.
Описание работы функции ФИШЕР в Excel
При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:
- не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
- имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.
Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:
Z"=1/2*ln(1+x)/(1-x)
Рассмотрим применение данной функции на 3-x конкретных примерах.
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции r xy ;
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение t р > t кр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.
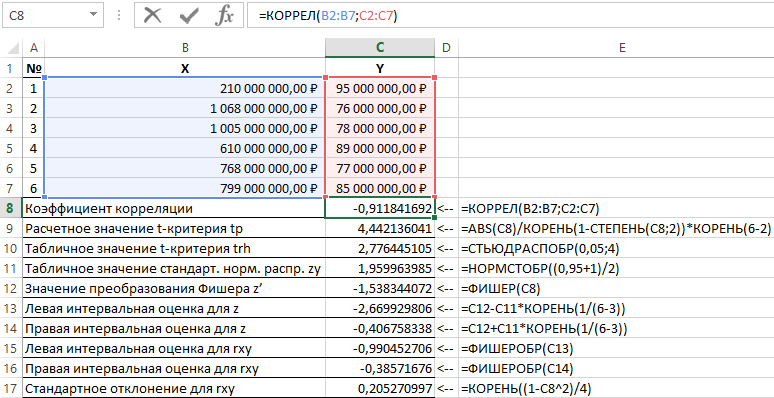
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н 0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н 1 о статистической значимости коэффициента детерминации:
Н 1: R 2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
Для этого используем в пакете Excel функцию:
FРАСПОБР (α;p;n-p-1)
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для F крит (см. рисунок 2).

Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что F расч > F крит. В итоге принимается гипотеза Н 1 о статистической значимости коэффициента детерминации.
Расчет величины показателя корреляции в Excel
Пример 3. Используя данные 23 предприятий о: X - цена на товар А, тыс. руб.; Y - прибыль торгового предприятия, млн. руб, производится изучение их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве модели регрессии.
Определим F крит из выражения:
F расч = R 2 /23*(1-R 2)
где R – коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение F расч = 46.
Для определения F крит используем распределение Фишера (см. рисунок 3).

Рисунок 3 – Пример расчетов.
Таким образом, полученная оценка уравнения регрессии надежна.
Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления F эмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
где - дисперсии первой и второй выборки соответственно.
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение F эмп всегда будет больше или равно единице.
Число степеней свободы определяется также просто:
k 1 =n l - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k 2 = n 2 - 1 для второй выборки.
В Приложении 1 критические значения критерия Фишера находятся по величинам k 1 (верхняя строчка таблицы) и k 2 (левый столбец таблицы).
Если t эмп >t крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос - есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
Таблица 3.
|
№№ учащихся |
Первый класс |
Второй класс |
Рассчитав дисперсии для переменных X и Y, получаем:
s x 2 =572,83; s y 2 =174,04
Тогда по формуле (8) для расчета по F критерию Фишера находим:
![]()
По таблице из Приложения 1 для F критерия при степенях свободы в обоих случаях равных k=10 - 1 = 9 находим F крит =3,18 (<3.29), следовательно, в терминах статистических гипотез можно утверждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
6.2 Непараметрические критерии
Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.
Для сравнения двух нормально распределенных совокупностей, у которых нет различий в средних выборочных значениях, но есть разница в дисперсиях, используют критерий Фишера . Фактический критерий рассчитывают по формуле:
где в числителе
стоит большее значение выборочной
дисперсии, а в знаменателе - меньшее.
Для вывода о достоверности различий
между выборками используют ОСНОВНОЙ
ПРИНЦИП
проверки статистических гипотез.
Критические точки для
 содержатся в таблице. Нулевую гипотезу
отвергают, если фактически установленная
величина
содержатся в таблице. Нулевую гипотезу
отвергают, если фактически установленная
величина превзойдет или окажется равной
критическому (стандартному) значению
превзойдет или окажется равной
критическому (стандартному) значению этой величины для принятого уровня
значимости
и числа
степеней свободы k
1
=
n
большая
-1
;
k
2
=
n
меньшая
-1
.
этой величины для принятого уровня
значимости
и числа
степеней свободы k
1
=
n
большая
-1
;
k
2
=
n
меньшая
-1
.
П р и м е р: при
изучении влияния некоторого препарата
на скорость проростания семян было
установлено, что в экспериментальной
партии семян и контроле средняя скорость
проростания одинакова, но есть разница
в дисперсиях. =1250,
=1250, =417.
Объемы выборок одинаковы и равны 20.
=417.
Объемы выборок одинаковы и равны 20.

 =2,12.
Следовательно, нулевая гипотеза
отвергается.
=2,12.
Следовательно, нулевая гипотеза
отвергается.
Корреляционная зависимость. Коэффициент корреляции и его свойства. Уравнения регрессии.
ЗАДАЧА корреляционного анализа сводится к:
Установлению направления и формы связи между признаками;
Измерению ее тесноты.
Функциональной называется однозначная зависимость между переменными величинами, когда определенному значению одной (независимой) переменнойх , называемой аргументом, соответствует определенное значение другой (зависимой) переменнойу , называемой функцией. (Пример : зависимость скорости химической реакции от температуры; зависимость силы притяжения от масс притягивающихся тел и расстояния между ними).
Корреляционной называется зависимость между переменными, имеющими статистистический характер, когда определенному значению одного признака (рассматриваемого в качестве независимой переменной) соответствует целый ряд числовых значений другого признака. (Пример : связь между урожаем и количеством осадков; между ростом и весом и т.д.).
Поле корреляции представляет собой множество точек, координаты которых равны полученным на опыте парам значений переменныхх иу .
По виду корреляционного поля можно судить о наличии или отсутствии связи и ее типе.




Связь называется положительной , если при увеличении одной переменной увеличивается другая переменная.
Связь называется отрицательной , если при увеличении одной переменной уменьшается другая переменная.
Связь называется
линейной
, если ее можно в
аналитическом виде представить как .
.
Показателем тесноты связи является коэффициент корреляции . Эмпирический коэффициент корреляции определяется выражением:

Коэффициент корреляции лежит в пределах от -1 до1 и характеризует степень близости между величинамиx иy . Если:

Корреляционную
зависимость между признаками можно
описывать разными способами. В частности,
любая форма связи может быть выражена
уравнением общего вида
 .
Уравнение вида
.
Уравнение вида и
и называютсярегрессией
. Уравнение
прямой регрессииу
нах
в общем случае можно записать в виде
называютсярегрессией
. Уравнение
прямой регрессииу
нах
в общем случае можно записать в виде

Уравнение прямой регрессии х нау в общем случае выглядит как

Наиболее вероятные значения коэффициентов а и в , с и d могут быть вычислены, например, при использовании метода наименьших квадратов.









